Как сделать равнобедренный тупоугольный треугольник
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Треугольник – многоугольник с тремя сторонами и тремя углами.

Угол ∠ A – угол, образованный сторонами A B и A C и противолежащий стороне B C .
Угол ∠ B – угол, образованный сторонами B A и B C и противолежащий стороне A C .
Угол ∠ C – угол, образованный сторонами C B и C A и противолежащий стороне A B .
Треугольник остроугольный , если все три угла в треугольнике острые.
Треугольник прямоугольный , если у него один из углов прямой ( = 90 ° ) .
Треугольник тупоугольный , если у него один из углов тупой.



Основные свойства треугольника:
- Против большей стороны лежит больший угол.
- Против равных сторон лежат равные углы.
- Сумма углов в треугольнике равна 180 ° .
- Если продолжить одну из сторон треугольника, например, A C , и взять на продолжении стороны точку D , образуется внешний угол ∠ B C D к исходному углу ∠ A C B .
Биссектриса угла – луч, выходящий из вершины угла и делящий его пополам.
Биссектриса треугольника – отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
Свойства биссектрис треугольника:
- Биссектриса угла – геометрическое место точек, равноудаленных от сторон угла.
- Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам:
Замечание: биссектриса угла – это луч, а биссектриса треугольника – отрезок.
Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Свойства медиан треугольника:
- Медиана разбивает треугольник на два равновеликих треугольника (два треугольника, имеющих одинаковую площадь).
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
Высота треугольника – это перпендикуляр, проведенный из вершины угла треугольника к прямой, содержащей противолежащую сторону этого треугольника.
Если треугольник остроугольный, то все три высоты будут лежать внутри треугольника. Если треугольник тупоугольный, то высоты, проведенные из вершин острых углов будут лежать вне треугольника, а высота, проведенная из вершины тупого угла будет лежать внутри треугольника.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство средней линии треугольника: средняя линия параллельна одной из его сторон и равна половине этой стороны.
Всего в треугольнике можно провести три средние линии. Три средние линии разбивают исходный треугольник на четыре равных треугольника. Площадь каждого маленького треугольника будет равна четверти площади большого треугольника.
Площадь произвольного треугольника можно найти следующими способами:
-
Полупроизведение стороны на высоту, проведенную к этой стороне.



Равнобедренным называется треугольник, у которого две стороны равны.
Равнобедренный треугольник может быть остроугольным, прямоугольным и тупоугольным.



Свойства равноберенного треугольника:
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведенные к основанию, совпадают.
Равносторонним называется треугольник, у которого все стороны и все углы равны.
Площадь равностороннего треугольника находится по формуле S = a 2 3 4
Высота равностороннего треугольника находится по формуле h = a 3 2
Треугольник называется прямоугольным, если у него один из углов равен 90 ° .
Свойства прямоугольного треугольника:
- Сумма двух острых углов треугольника равна 90 ° .
- Катет, лежащий напротив угла в 30 ° , равен половине гипотенузы.
- Если катет равен половине гипотенузы, он лежит напротив угла в 30 ° .
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
У прямоугольного треугольника катеты перпендикулярны друг другу, следовательно, площадь можно найти по формуле:
Как различать треугольники: прямоугольный, тупоугольный, остроугольный?
Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Виды треугольников по величине углов
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.
Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.
Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.
Основная и дополнительная литература:
2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.
Теоретический материал для самостоятельного изучения

Давайте вспомним, что вы уже знаете о видах треугольников.
По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.
Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон. Ведь у каждого есть ещё и по три угла.
У вас уже появились идеи?
Острые – меньше прямого
Прямые – угол 90 градусов
Тупые – больше прямого

Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:
те, у которых все углы острые, – остроугольные,
те, у которых есть прямой угол, – прямоугольные,
те, у которых есть тупой угол, – тупоугольные.
Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.
Обычно вид треугольника можно определить на глаз.
Попробуйте определить виды треугольников по величине углов без измерений.

Прямоугольный –1, 3
тупоугольный– 2, 4, 7, 5
По величине углов различают 3 вида треугольников:
Остроугольные, прямоугольные и тупоугольные

Определить вид треугольника можно тремя способами:
с помощью измерений, на глаз и по условным обозначениям.
Задания тренировочного модуля
Закончите предложения:
Остроугольный треугольник – это треугольник, у которого ……………………
Прямоугольный треугольник – это треугольник, у которого есть ……………………
Тупоугольный треугольник – треугольник, все стороны которого есть ……………………
Остроугольный треугольник — это треугольник, у которого все углы острые.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:
Как различать треугольники: прямоугольный, тупоугольный, остроугольный?
Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Виды треугольников по величине углов
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.
Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.
Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.
Основная и дополнительная литература:
2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.
Теоретический материал для самостоятельного изучения

Давайте вспомним, что вы уже знаете о видах треугольников.
По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.
Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон. Ведь у каждого есть ещё и по три угла.
У вас уже появились идеи?
Острые – меньше прямого
Прямые – угол 90 градусов
Тупые – больше прямого

Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:
те, у которых все углы острые, – остроугольные,
те, у которых есть прямой угол, – прямоугольные,
те, у которых есть тупой угол, – тупоугольные.
Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.
Обычно вид треугольника можно определить на глаз.
Попробуйте определить виды треугольников по величине углов без измерений.

Прямоугольный –1, 3
тупоугольный– 2, 4, 7, 5
По величине углов различают 3 вида треугольников:
Остроугольные, прямоугольные и тупоугольные

Определить вид треугольника можно тремя способами:
с помощью измерений, на глаз и по условным обозначениям.
Задания тренировочного модуля
Закончите предложения:
Остроугольный треугольник – это треугольник, у которого ……………………
Прямоугольный треугольник – это треугольник, у которого есть ……………………
Тупоугольный треугольник – треугольник, все стороны которого есть ……………………
Остроугольный треугольник — это треугольник, у которого все углы острые.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Типы треугольников
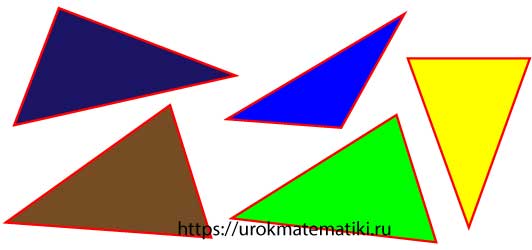
По величине углов
Остроугольный треугольник

— все углы треугольника острые.
Тупоугольный треугольник

— один из углов треугольника тупой (больше 90°).
Прямоугольный треугольник

— один из углов треугольника прямой (равен 90°).
По числу равных сторон
Разносторонний треугольник
— все три стороны не равны.
Равнобедренный треугольник

— две стороны равны.
Равносторонний (правильный) треугольник

— все три стороны равны.
Вершины, углы и стороны треугольника
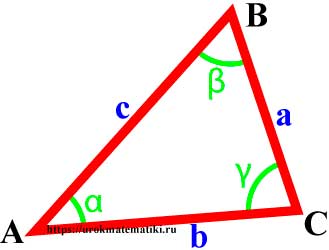
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы
- если α > β , тогда a > b
- если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
a sin α = b sin β = c sin γ
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 - 2 b c · cos α
b 2 = a 2 + c 2 - 2 a c · cos β
c 2 = a 2 + b 2 - 2 a b · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α;
c = a cos β + b cos α;
Формулы для вычисления длин сторон треугольника
Формулы сторон через медианы
a = 2 3 2 m b 2 + m c 2 - m a 2
b = 2 3 2 m a 2 + m c 2 - m b 2
c = 2 3 2 m a 2 + m b 2 - m c 2
Медианы треугольника
Медиана треугольника — отрезок внутри треугольника, который соединяет вершину треугольника с серединой противоположной стороны.

Свойства медиан треугольника
- Медианы треугольника пересекаются в одной точке. Точка пересечения медиан называется центроидом.
S ∆AOF = S ∆AOE = S ∆BOF = S ∆BOD = S ∆COD = S ∆COE
Формулы медиан треугольника
Формулы медиан треугольника через стороны
m a = 1 2 2 b 2 + 2 c 2 - a 2
m b = 1 2 2 a 2 + 2 c 2 - b 2
m c = 1 2 2 a 2 + 2 b 2 - c 2
Биссектрисы треугольника
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
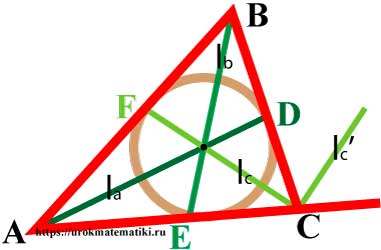
Свойства биссектрис треугольника
- Биссектрисы треугольника пересекаются в одной точке, равноудаленной от трех сторон треугольника, - центре вписанной окружности.
Угол между l c и l c ' = 90°
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны
l a = 2 b c p p - a b + c
l b = 2 a c p p - b a + c
l c = 2 a b p p - c a + b
где p = a + b + c 2 — полупериметр треугольника.
Формулы биссектрис треугольника через две стороны и угол
l a = 2 b c cos α 2 b + c
l b = 2 a c cos β 2 a + c
l c = 2 a b cos γ 2 a + b
Высоты треугольника
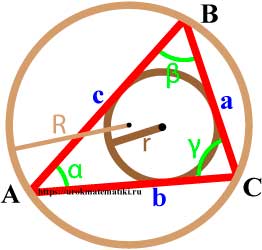
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону.
В зависимости от типа треугольника высота может содержаться:
- внутри треугольника — для остроугольного треугольника;
- совпадать с его стороной — для катета прямоугольного треугольника;
- проходить вне треугольника — для острых углов тупоугольного треугольника.
Свойства высот треугольника
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Формулы высот треугольника
Формулы высот треугольника через сторону и угол
h a = b sin γ = c sin β
h b = c sin α = a sin γ
h c = a sin β = b sin α
Формулы высот треугольника через сторону и площадь
Формулы высот треугольника через две стороны и радиус описанной окружности
Окружность вписанная в треугольник
Окружность называется вписанной в треугольник, если она касается всех трех его сторон.
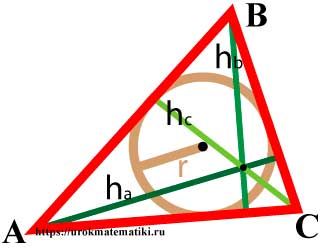
Свойства окружности вписанной в треугольник
- Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
- В любой треугольник можно вписать окружность, и только одну.
Формулы радиуса окружности вписанной в треугольник
Радиус вписанной в треугольник окружности равен отношению площади треугольника к его полупериметру
Радиус вписанной в треугольник окружности через три стороны
Формулы высот треугольника через две стороны и радиус описанной окружности
Окружность описанная вокруг треугольника
Окружность называется описанной вокруг треугольника, если она содержит все вершины треугльника.
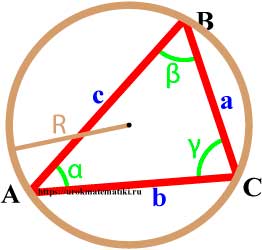
Свойства окружности описанной вокруг треугольника
- Центр описанной вокруг треугольника окружности лежит на пересечении серединных перпендикуляров к его сторонам.
- Вокруг любого треугольника можно описать окружность, и только одну.
Свойства углов
Центр описанной окружности лежит внутри остроугольного треугольника, снаружи тупоугольнго треугольника, на середине гипотенузы прямоугольного треугольника.
Формулы радиуса окружности описанной вокруг треугольника
Радиус описанной окружности через три стороны и площадь
Радиус описанной окружности через площадь и три угла
Радиус описанной окружности через сторону и противоположный угол (теорема синусов)
Связь между вписанной и описанной окружностями треугольника
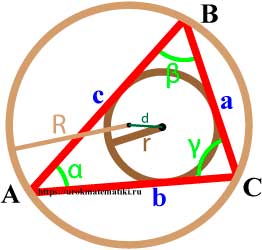
Формулы радиуса окружности описанной вокруг треугольника
Если d — расстояние между центрами вписанной и описанной окружностей, то
d 2 = R 2 - 2 R r
Радиус описанной окружности через площадь и три угла
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон треугольника.
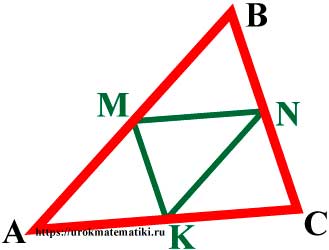
Свойства средней линии треугольника
- Любой треугольник имеет три средних линии.
- Средняя линия треугольника параллельна основанию и равна его половине.
MN = 1 2 AC ; KN = 1 2 AB ; KM = 1 2 BC
Признаки
Если отрезок параллелен одной из сторон треугольника и соединяет середину стороны треугольника с точкой, лежащей на другой стороне треугольника, то этот отрезок — средняя линия.
Периметр треугольника
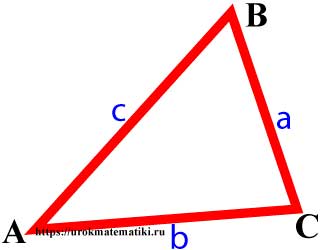
Периметр треугольника ∆ABC равен сумме длин его сторон.
Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.
S = 1 2 a · h a ,
S = 1 2 b · h b ,
S = 1 2 c · h c ,
где a, b, c — стороны треугольника,
ha, hb, hc — высоты, проведенные к сторонам a, b, c треугольника.
Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .
S = p p - a p - b p - c ,
где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
S = 1 2 a · b · sin γ ,
S = 1 2 b · c · sin α ,
S = 1 2 a · c · sin β ,
где a, b, c — стороны треугольника,
γ — угол между сторонами a и b ,
α — угол между сторонами b и c ,
β — угол между сторонами a и c .
Формула площади треугольника по трем сторонам и радиусу описанной окружности
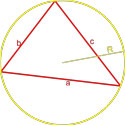
S = a · b · c 4 R ,
a, b, c — стороны треугольника,
R - радиус описанной окружности.
Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
где S — площадь треугольника,
r - радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2
Равенство треугольников
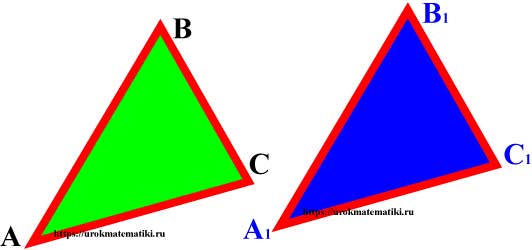
Определение
Если два треугольника АВС и А1В1С1 можно совместить наложением, то они равны.
Свойства
У равных треугольников равны и их соответствующие элементы. (В равных треугольниках против равных сторон лежат равные углы, против равных углов лежат равные стороны).
Признаки равенства треугольников
По двум сторонам и углу между ними
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим углам
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По трем сторонам
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Подобие треугольников
Определение
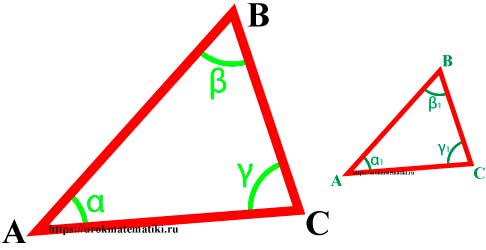
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
∆АВС ~ ∆MNK => α = α 1 , β = β 1 , γ = γ 1 и AB MN = BC NK = AC MK = k
где k — коэффициент подобия.
Признаки подобия треугольников
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, между этими сторонами, равны, то такие треугольники подобны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
S ∆АВС S ∆MNK = k 2
Прямоугольные треугольники
Прямоугольный треугольник — треугольник, в котором один угол прямой (то есть равен 90˚).
Свойства прямоугольного треугольника
-
Сумма двух острых углов прямоугольного треугольника равна 90°.
Сумма углов треугольника равна 180°, а прямой угол равен 90°, поэтому сумма двух острых углов прямоугольного треугольника ∠ 1 + ∠ 2 = 90° .
Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы (гипотенуза в два раза длиннее катета, лежащего против угла в 30°).
Рассмотрим прямоугольный треугольник ABC, в котором ∠ A — прямой, ∠ B = 30°, и значит, что ∠ C = 60°.
Докажем, что BC=2AC.
Приложим к треугольнику ABC равный ему треугольник ABD , как показано на рисунке.
Получим треугольник BCD, в котором ∠ B = ∠ D = 60° , поэтому DC = BC. Но DC = 2AC. Следовательно, BC = 2AC.
Справедливо и обратное суждение: Если катет прямоугольного треугольника равен половине гипотенузы (или гипотенуза в два раза длиннее катета), то угол, лежащий против этого катета, равен 30°.
Признаки равенства прямоугольных треугольников
Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из общих признаков равенства треугольников для прямоугольных треугольников можно сформулировать свои признаки равенства.
- Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
- Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
- Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Свойства
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Читайте также:


