Как сделать равнобедренный треугольник в с
\u0420\u0430\u0432\u043d\u043e\u0431\u0435\u0434\u0440\u0435\u043d\u043d\u044b\u0439 - \u0438\u043c\u0435\u0435\u0442 \u043e\u0441\u043d\u043e\u0432\u0430\u043d\u0438\u0435 \u0438 \u0434\u0432\u0435 \u0440\u0430\u0432\u043d\u044b\u0435 \u0441\u0442\u043e\u0440\u043e\u043d\u044b.
\u041b\u0435\u0433\u043a\u043e \u043f\u043e\u0441\u0442\u0440\u043e\u0438\u0442\u044c \u043f\u0440\u0438 \u043f\u043e\u043c\u043e\u0449\u0438 \u0446\u0438\u0440\u043a\u0443\u043b\u044f. \u0427\u0435\u0440\u0442\u0438\u043c \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u043b\u044c\u043d\u044b\u0439 \u043e\u0442\u0440\u0435\u0437\u043e\u043a - \u044d\u0442\u043e \u043e\u0441\u043d\u043e\u0432\u0430\u043d\u0438\u0435. \u0426\u0438\u0440\u043a\u0443\u043b\u044c \u043e\u0442\u043a\u0440\u044b\u0432\u0430\u0435\u043c \u043d\u0430 \u043d\u0443\u0436\u043d\u0443\u044e \u0432\u0435\u043b\u0438\u0447\u0438\u043d\u0443, \u0438\u0433\u043b\u0443 \u0441\u0442\u0430\u0432\u0438\u043c \u043d\u0430 \u043d\u0430\u0447\u0430\u043b\u043e \u043e\u0442\u0440\u0435\u0437\u043a\u0430. \u041f\u0440\u043e\u0432\u043e\u0434\u0438\u043c \u0434\u0443\u0433\u0443 \u043d\u0430\u0434 \u043e\u0442\u0440\u0435\u0437\u043a\u043e\u043c. \u041f\u0435\u0440\u0435\u0441\u0442\u0430\u0432\u043b\u044f\u0435\u043c \u0438\u0433\u043b\u0443 \u043d\u0430 \u0434\u0440\u0443\u0433\u043e\u0439 \u043a\u043e\u043d\u0435\u0446 \u043e\u0442\u0440\u0435\u0437\u043a\u0430 \u0438 \u043f\u043e\u0432\u0442\u043e\u0440\u044f\u0435\u043c. \u0422\u043e\u0447\u043a\u0430 \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0435\u043d\u0438\u044f \u044d\u0442\u0438\u0445 \u0434\u0432\u0443\u0445 \u0434\u0443\u0433 \u0431\u0443\u0434\u0435\u0442 \u0432\u0435\u0440\u0448\u0438\u043d\u043e\u0439 \u0442\u0440\u0435\u0443\u0433\u043e\u043b\u044c\u043d\u0438\u043a\u0430. \u0421\u043e\u0435\u0434\u0438\u043d\u044f\u0435\u0448\u044c \u0441 \u043d\u0430\u0447\u0430\u043b\u043e\u043c \u0438 \u043a\u043e\u043d\u0446\u043e\u043c \u043e\u0441\u043d\u043e\u0432\u0430\u043d\u0438\u044f - \u043f\u043e\u043b\u0443\u0447\u0430\u0435\u0442\u0441\u044f \u0440\u0430\u0432\u043d\u043e\u0431\u0435\u0434\u0440\u0435\u043d\u043d\u044b\u0439 \u0442\u0440\u0435\u0443\u0433\u043e\u043b\u044c\u043d\u0438\u043a.
\u041e\u0441\u0442\u0440\u043e\u0443\u0433\u043e\u043b\u044c\u043d\u044b\u0439 - \u0438\u043c\u0435\u0435\u0442 \u043e\u0441\u0442\u0440\u044b\u0435 \u0443\u0433\u043b\u044b, \u0442.\u0435. \u043c\u0435\u043d\u044c\u0448\u0435 90\u00b0.
\u041f\u0440\u043e\u0432\u043e\u0434\u0438\u043c \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u043b\u044c\u043d\u044b\u0439 \u043e\u0442\u0440\u0435\u0437\u043e\u043a. \u041e\u0442 \u043e\u0431\u043e\u0438\u0445 \u043a\u043e\u043d\u0446\u043e\u0432 \u043f\u0440\u043e\u0432\u043e\u0434\u0438\u043c \u043b\u0443\u0447\u0438, \u043c\u0435\u043d\u044c\u0448\u0435 90\u00b0, \u043f\u043e \u043d\u0430\u043f\u0440\u0430\u0432\u043b\u0435\u043d\u0438\u044e \u0434\u0440\u0443\u0433 \u043a \u0434\u0440\u0443\u0433\u0443. \u041f\u0440\u0438 \u044d\u0442\u043e\u043c \u043e\u043d\u0438 \u0434\u043e\u043b\u0436\u043d\u044b \u0431\u044b\u0442\u044c \u0431\u043e\u043b\u044c\u0448\u0435, \u0447\u0435\u043c \u043e\u0441\u043d\u043e\u0432\u0430\u043d\u0438\u0435.
\u041f\u0440\u0438 \u043f\u043e\u043c\u043e\u0449\u0438 \u0446\u0438\u0440\u043a\u0443\u043b\u044f \u043d\u0430\u0447\u0435\u0440\u0442\u0438\u0442\u044c \u043e\u043a\u0440\u0443\u0436\u043d\u043e\u0441\u0442\u044c. \u041f\u043e\u0441\u0442\u0440\u043e\u0438\u0442\u044c, \u043a\u0430\u043a \u043f\u043e\u043a\u0430\u0437\u0430\u043d\u043e \u043d\u0430 \u0440\u0438\u0441\u0443\u043d\u043a\u0430. ">]" data-testid="answer_box_list">
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
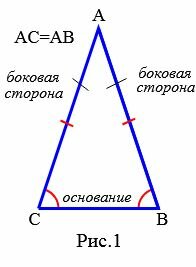
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (\( \small \angle A \) ) называется вершинным углом. Углы между основанием и боковыми сторонами (\( \small \angle B, \ \angle C \) ) называются углами при основании.
 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
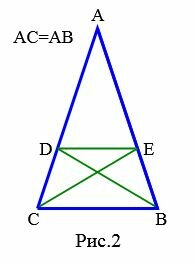 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что \( \small \angle B= \angle C. \) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол \( \small \angle A \) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
Из \( \small AB=AC\) и \( \small AD=AE \) следует:
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: \( \small CE=BD,\) \( \small CD=BE ,\) сторона \( \small BC \) общая. Отсюда следует, что

Из (2) и (4) следует, что \( \small \angle B= \angle C. \)
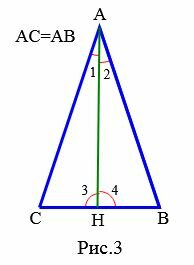 |

Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису \( \small AH \) треугольника. Тогда \( \small \angle CAH=\angle BAH. \) Докажем, что \( \small \angle B= \angle C. \) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle CAH=\angle BAH. \) Отсюда следует: \( \small \angle B= \angle C. \)
Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.

Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle 1=\angle 2. \) Тогда \( \small CH=HB, \) \( \small \angle 3=\angle 4. \) Равенство \( \small CH=HB \) означает, что \( \small AH \) является также медианой треугольника ABC. Углы \( \small \angle 3\) и \( \angle 4 \) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда \( \small AH \) является также высотой треугольника \( \small ABC. \) Поскольку высота \( \small AH \) перпендикулярна к \( \small BC \) и \( \small CH=HB, \) то \( \small AH \) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
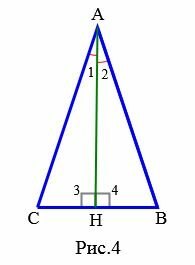
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (первый признак равенства треугольников): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
  |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
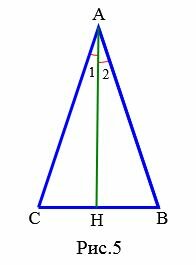
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда
Применим теорему синусов для треугольника \( \small AHC \):
Применим теорему синусов для треугольника \( \small AHB \):
тогда, из (5), (6), (7) получим:
Следовательно \( \small \sin \angle C= \sin \angle B. \) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) \( \small \angle C= \angle B, \) 2) \( \small \angle C= 180° - \angle B. \) Поскольку сумма двух углов треугольника меньше 180°: \( \small \angle C + \angle B Доказательство (Вариант 2). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой, т.е. \( \small \angle 1=\angle 2, \) \( \small CH=HB \) (Рис.6). На луче \( \small AH \) отложим отрезок \( \small HD \) так, чтобы \( \small AH=HD. \) Соединим точки \( \small C \) и \( \small D. \)
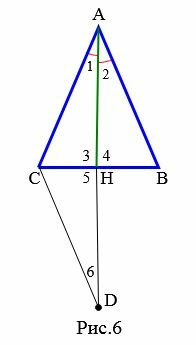 |

Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.
1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Задачи и решения
Задача 1. Известны основание \( \small a=5 \) и высота \( \small h=6 \) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
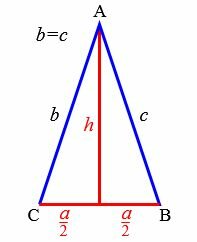 |
Решение. Найдем боковые стороны \( \small b \) и \( \small c \) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
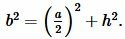 |
Подставляя значения \( \small a \) и \( \small h \) в (9), получим:
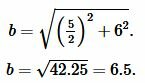 |
Боковая сторона \( \small c \) равнобедренного треугольника равна:
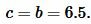 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
Подставляя значения \( \small a=5, \) \( \small b=6.5 \) и \( \small c=6.5 \) в (10), получим:
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

АВ = ВС — боковые стороны
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Доказательство теоремы:
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство теоремы:

Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника

Формулы длины стороны (основания — b):
- b = 2a \sin( \beta /2)= a \sqrt
- b = 2a \cos \alpha
Формулы длины равных сторон — (а):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Площадь равнобедренного треугольника

Формула площади треугольника через высоту h и основание b, (S):

Поговорим, казалось бы, о такой мелочи в системе преподавания геометрии 7 класса, как рисунок равнобедренного треугольника. Если Вы репетитор по математике – попросите Вашего ученика нарисовать такой треугольник. Как он это сделает? С вероятностью, равной 0,9 порядок проведения линий (сторон) на бумаге будет соответствовать последовательности расположения вершин треугольника в записи , то есть направлению стрелки, показанной на рисунке:
Именно так (то есть по кругу) сам репетитор по математике обозначает вершины и именно этот порядок запоминается. Понаблюдаем за учеником. Сначала, скорее всего, он нарисует репетитору математики левую боковую сторону, затем правую, а уже после этого соединит их нижние точки и нарисует основание. Все бы ничего, да вот проблема: трудно изображать боковые стороны равными (особенно если использовать непрозрачную линейку) и поэтому рисунок часто получается несимметричным. И вот ученик уже работает ластиком (в лучшем случае) и, как следствие, тратит на чертеж драгоценное время (пусть незначительное, но все-таки). Хороший репетитор по математике стремится использовать каждую свободную минуту своего занятия и поэтому всегда уделяет внимание оптимизации самостоятельной работы учащегося. Использование методики готовых чертежей не является панацеей, тем более в период, когда ребенок учится в 7 классе. В этом возрасте он приобретает чертежные навыки, и если репетитор по математике будет баловать его готовыми чертежами, то при классических формах подачи заданий, составляющих большую часть контрольных работ, ученик может растеряться.
Поэтому важно научить быстро и точно выполнять стандартные рисунки. Но как?
Есть одно простое правило. Оно не только ускорит построение равнобедренного треугольника, но и будет способствовать запоминанию его главных характеристик и свойств. Я предполагаю, что для этого имеется бумага в клеточку, линейка и карандаш.
Как репетитор по математике рисует равнобедренный треугольник?
Какие девиденты приносит это построение репетитору по математике?
Каждый раз, когда ученик отмечает вершины по данному плану, репетитор по математике напоминает ему о том, что вертикальный отрезок есть ни что иное, как медиана, биссектриса и высота треугольника. Многократные построения и напоминания репетитора пойдут только на пользу ученику, ибо заставят вспомнить важнейшее свойство равнобедренного треугольника. Ученик поймет и запомнит форму изучаемой фигуры, особенности и взаимосвязи ее элементов. Сильный семиклассник задумается (или догадается спросить у репетитора) о том, почему построенный таким образом треугольник обязательно окажется равнобедренным.
Часто в задачах по геометрии в 7 классе фигурирует произвольный треугольник. Я всегда советую своим ученикам строить его так, чтобы они значительно отличался по виду от равнобедренного. Почему? Если от центральной точки (от основания высоты), отложить влево и вправо разные отрезки даже с разницей в клетку, то, несмотря на несовпадение медианы с высотой, образованные ими треугольники окажутся чрезвычайно узкими и поэтому неудобными для любых демонстраций. Репетитор по математике просто не сможет в них ничего показать. Посмотрите, насколько близко оказываются друг от друга отрезки BH, BN и BM на рисунке, изображенном слева. И чем ближе изображение в виду равнобедренного треугольника, тем ближе они будут друг к другу. Об этом репетитор по математике предупреждает ученика уже в 7 классе. Дети легко принимают за истину то, что кажется верным по рисунку. Так высоту, приходящую в кажущуюся середину стороны школьники легко принимают за медиану. В будущем, когда подготовка к ЕГЭ по математике поставит перед репетитором задачу научить ребенка решать номера С4, навыки изображения треугольников общего вида будут весьма полезны. Рисуйте равнобедренный треугольник только тогда, когда он дан в условии. Если имеется треугольник общего вида — изобразите его удлиненным в одну из сторон относительно основания высоты.
Читайте также:


