Как сделать расчет в таблице excel
Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса - другое дело, а для обычных людей мышеловка"деньги за 15 минут, нужен только паспорт" срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это "потом" все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?
Так что очень надеюсь, что изложенный ниже материал вам не пригодится.
Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. "Помассажировать числа" заранее, как я это называю :) Microsoft Excel может сильно помочь в этом вопросе.
Вариант 1. Простой кредитный калькулятор в Excel
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами - таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial) . Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

- Ставка - процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
- Кпер - количество периодов, т.е. срок кредита в месяцах.
- Пс - начальный баланс, т.е. сумма кредита.
- Бс - конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
- Тип - способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

Вариант 2. Добавляем детализацию
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel - ОСПЛТ (PPMT) и ПРПЛТ (IPMT) . Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:


Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку ("") в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:
=ЕСЛИ(A18<>""; текущая формула; "")
Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

Вариант 3. Досрочное погашение с уменьшением срока или выплаты
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.
В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять - не достигли мы нулевого баланса раньше срока:

А в случае уменьшения выплаты - заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами
Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:
При ведении большинства таблиц в Excel, спустя некоторое время, нужно посчитать итог отдельных столбцов или всего рабочего документа. Однако, если делать это вручную, процесс может затянуться на несколько часов, легко допустить ошибки. Чтобы получить максимально точный результат и сэкономить время, можно автоматизировать свои действия через встроенные инструменты программы.
Способы подсчета итогов в рабочей таблице
Существует несколько проверенных способов расчета итогов для отдельных столбцов таблицы или одновременно нескольких колонок. Самый простой метод – выделение значений мышкой. Достаточно выделить числовые значения одного столбца мышкой. После этого в нижней части программы, под строчкой выбора листов можно будет увидеть сумму чисел из выделенных клеток.
Если же нужно не только увидеть итоговую сумму чисел, но и добавить результат в рабочую таблицу, необходимо использовать функцию автосуммы:
- Выделить диапазон клеток, итог сложения которых нужно получить.
- На вкладке “Главная” в правой стороне найти значок автосуммы, нажать на него.

- После выполнения данной операции результат появится в клетке под выделенным диапазоном.
Еще одна полезная особенность автосуммы – возможность получения результатов под несколькими смежными столбцами с данными. Два варианта подсчета итогов:
- Выделить все ячейки под столбцами, сумму из которых нужно получить. Нажать на значок автосуммы. Результаты должны появиться в выделенных клетках.
- Отметить все столбцы, из которых необходимо рассчитать итог вместе с пустыми клетками под ними. Нажать на значок автосуммы. В свободных клетках появится результат.
Важно! Единственный недостаток функции “Автосумма” – с ее помощью невозможно считать итоги отдельных ячеек или столбцов, которые расположены далеко друг от друга.
Чтобы рассчитать результаты для отдельных ячеек или столбцов, необходимо воспользоваться функцией “СУММ”. Порядок действий:
- Отметить нажатием ЛКМ ту ячейку, куда нужно вывести результат расчета.
- Кликнуть по символу добавления функции.

- После этого должно открыться окно настройки “Мастер функций”. Из открывшегося списка необходимо выбрать требуемую функцию “СУММ”.
- Для выхода из окна “Мастер функций” нажать кнопку “ОК”.
Далее необходимо настроить аргументы функции. Для этого в свободном поле нужно ввести координаты ячеек, сумму которых требуется посчитать. Чтобы не вводить данные вручную, можно использовать кнопку справа от свободного поля. Ниже первого свободного поля находится еще одна пустая строчка. Она предназначена для выполнения расчета для второго массива данных. Если нужна информация только по одному диапазону ячеек, ее можно оставить пустой. Для завершения процедуры нужно нажать на кнопку “ОК”.

Как посчитать промежуточные итоги
Одна из частых ситуаций, с которой сталкиваются люди, активно работающие в таблицах Excel, – необходимость посчитать промежуточные итоги в одном рабочем документе. Как и в случае с общим итогом, сделать это можно вручную. Однако программа позволяет автоматизировать свои действия, быстро получить требуемый результат. Существует несколько требований, которым должна соответствовать таблица для расчета промежуточных итогов:
- При создании шапки столбца нельзя вписывать в ней несколько строк. Одновременно с этим шапка должна быть расположена на первой строке рабочей таблицы.
- Невозможно получить промежуточные итоги в тех столбцах, внутри которых находятся пустые ячейки. Даже при наличии одной пустой клетки во всей таблице, расчет произведен не будет.
- Рабочий документ должен иметь стандартный диапазон без форматирования.
Сам процесс расчета промежуточных итогов состоит из нескольких действий:
- В первую очередь нужно распределить данные в первом столбце так, чтобы они распределились на группы одинакового типа.
- Левой кнопкой мыши выбрать любую произвольную ячейку рабочей таблицы.
- Перейти во вкладку “Данные” на основной странице с инструментами.
- В разделе “Структура” нажать на функцию «Промежуточные итоги”.
- После осуществления данных действий на экране появится окно, в котором необходимо прописать параметры для дальнейшего расчета.
В параметре “Операция” необходимо выбрать раздел “Сумма” (есть возможность выбора других математических действий). В следующем параметре указать те столбцы, для которых будут высчитываться промежуточные итоги. Для сохранения указанных параметров необходимо нажать кнопку “ОК”. После выполнения описанных выше действий, между каждой группой ячеек появится одна промежуточная, в которой будет указан результат, полученный после осуществления расчета.
Важно! Еще один способ получения промежуточных итогов – через отдельную функцию “ПРОМЕЖУТОЧНЫЕ.ИТОГИ”. Данная функция совмещает в себе несколько алгоритмов расчета, которые необходимо прописывать в выбранной ячейке через строку функций.
Как удалить промежуточные итоги
Необходимость в существовании промежуточных итогов со временем полностью пропадает. Чтобы лишние значения не отвлекали человека во время работы, таблица получила изначальную целостность, нужно удалить результаты расчетов с их дополнительными строчками. Для этого необходимо выполнить несколько действий:
- Зайти во вкладку “Данные” на главной странице с инструментами. Нажать на функцию “Промежуточный итог”.
- В появившемся окне необходимо отметить галочкой пункт “Размер”, нажать на кнопку “Убрать все”.
- После этого все добавленные данные вместе с дополнительными ячейками будут удалены.

Заключение
Выбор способа получения итогов рабочей таблицы Excel напрямую зависит от того, где находятся требуемые для расчета данные, нужно ли заносить результаты в таблицу. Ответив на эти вопросы, можно выбрать наиболее подходящий метод из описанных выше, повторить процедуру согласно подробной инструкции.
Одна из лучших реализаций табличного редактора Excel, если не самая лучшая. В нём можно выполнять простейшие и сложнейшие математические операции, с финансовыми и логическими и текстовыми формулами, создавать эффектные диаграммы, делать сводные таблицы и много прочего. Давайте рассмотрим, как работать с простейшими арифметическими операциями в Excel.
Работать с простейшими арифметическими операциями в Excel может любой пользователь компьютера, для этого не требуется профильное образование. Это как работать с калькулятором, только более удобным и более гибким. Таблицы же в Excel помогут нам в любых жизненных ситуациях, которые нам буквально нужно просчитать. Это банально могут быть списки и подсчёты покупки еды и каких-то повседневных вещей, списки и подсчёты сданных денег на школьный ремонт или какое-то прочее общественное дело. А могут быть сметы на ремонт или строительство жилья, фиксация движения вверенных подотчётных денег и подобного рода значимые ситуации. Все эти списки не нужно хранить где-то в блокнотах или заметках и потом скрупулёзно высчитывать на калькуляторе все их пункты. Эти списки можно вести в программе Excel, в ней же и проводить все необходимые подсчёты.
Базовые арифметические операции в Excel – это:
Excel как калькулятор
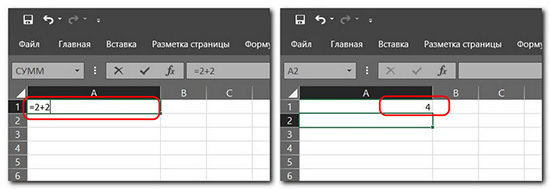
Можем произвести более сложное вычисление.
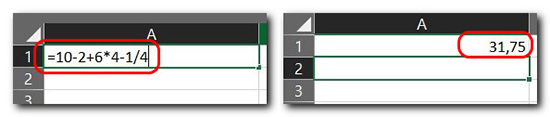
Если вычисление нужно скорректировать или доработать, тогда кликаем ячейку с результатом. Делаем клик в строке формул Excel, изменяем или довычисляем что нужно. Жмём Enter.
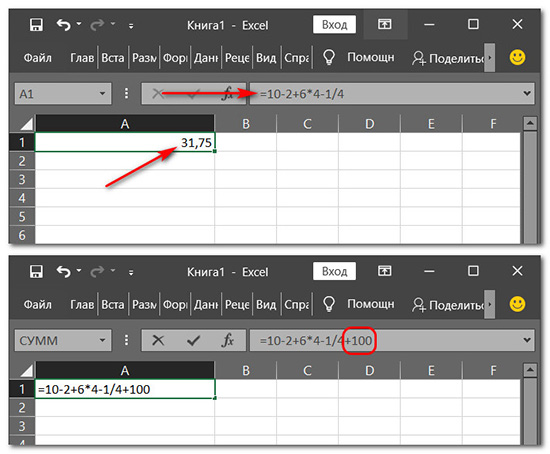
Арифметические операции с данными таблицы
По аналогии с этим примером теперь можем, кликом мыши указывая ячейки со значениями в любых местах таблицы Excel, выполнять вычитание, умножение, деление, возведение в степень и также другие, более сложные комбинированные вычисления. И также потом можем корректировать и дописывать формулы.
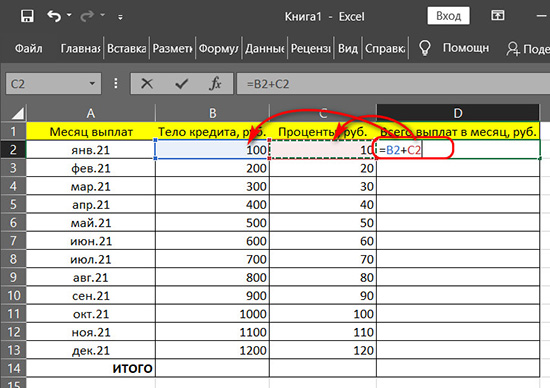
Но вернёмся к нашему примеру с расчётом кредита. Далее нам нужно сложить тело кредита и проценты для каждого месяца. Но нам не нужно в ячейке общей суммы каждого месяца проделывать операцию сложения двух предшествующих ячеек. Мы просто копируем ячейку общей суммы первого месяца и вставляем скопированное в ячейки общей суммы остальных месяцев. По умолчанию у нас скопируется не значение ячейки первого месяца, а формула. Формула сложения ячеек по столбцам передастся во все указанные нами для вставки ячейки. И у нас для каждого месяца будет свой результат, исходящий из иных значений тела кредита и процентов.
Альтернативный же вариант – это кликаем ячейку формулы, наводим курсор в её правый нижний угол до превращения курсора в жирный плюс и оттягиваем этот плюс до нужной ячейки.
И мы получим итоговые суммы.
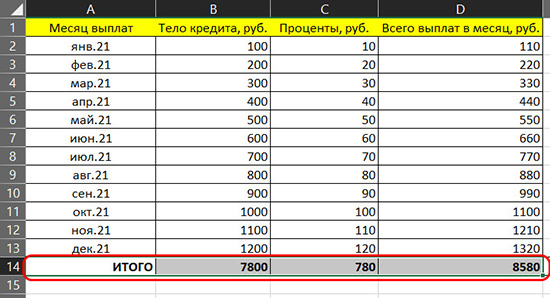
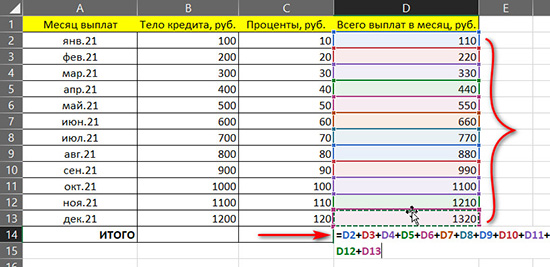
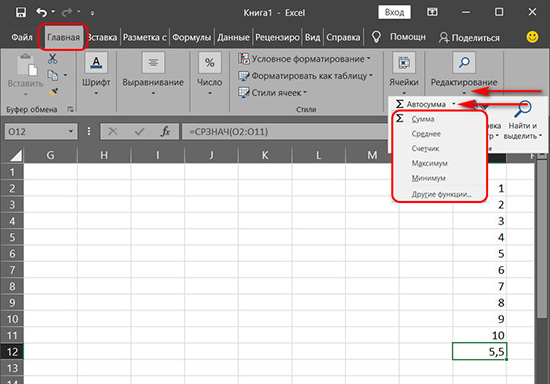
Но можно поступить проще и при сложении подряд идущих ячеек (вертикально, горизонтально – не важно) использовать функцию автосуммы.
Автосумма
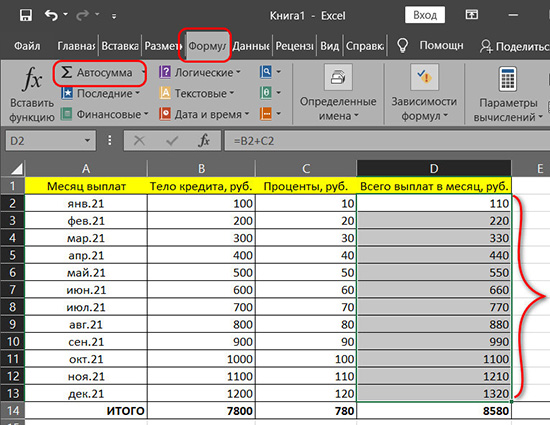
Значок автосуммы также вынесен на главную вкладку панели инструментов. Но непосредственно автосумма – это только основная из всей подборки операций. В выпадающем списке автосуммы мы можем выбрать и другие операции, которые можно провести с идущими подряд ячейками – вычисление среднего значения, определение минимального или максимального значения, подсчёт выделенных ячеек.
Если у вас остались вопросы, оставляйте их в комментариях ниже. А пока… пока.
Под описательной статистикой понимают систематизацию эмпирических данных по целому ряду основных статистических критериев. Причем на основе полученного результата из этих итоговых показателей можно сформировать общие выводы об изучаемом массиве данных.
- Медиана;
- Мода;
- Дисперсия;
- Среднее;
- Стандартное отклонение;
- Стандартная ошибка;
- Асимметричность и др.
Рассмотрим, как работает данный инструмент на примере Excel 2010, хотя данный алгоритм применим также в Excel 2007 и в более поздних версиях данной программы.



Размах вариации
Размах вариации – разница между максимальным и минимальным значением:

Ниже приведена графическая интерпретация размаха вариации.

Видно максимальное и минимальное значение, а также расстояние между ними, которое и соответствует размаху вариации.
С одной стороны, показатель размаха может быть вполне информативным и полезным. К примеру, максимальная и минимальная стоимость квартиры в городе N, максимальная и минимальная зарплата по профессии в регионе и проч. С другой стороны, размах может быть очень широким и не иметь практического смысла, т.к. зависит лишь от двух наблюдений. Таким образом, размах вариации очень неустойчивая величина.
Вычисление коэффициента вариации
Этот показатель представляет собой отношение стандартного отклонения к среднему арифметическому. Полученный результат выражается в процентах.
В Экселе не существует отдельно функции для вычисления этого показателя, но имеются формулы для расчета стандартного отклонения и среднего арифметического ряда чисел, а именно они используются для нахождения коэффициента вариации.
Шаг 1: расчет стандартного отклонения
Стандартное отклонение, или, как его называют по-другому, среднеквадратичное отклонение, представляет собой квадратный корень из дисперсии. Для расчета стандартного отклонения используется функция СТАНДОТКЛОН. Начиная с версии Excel 2010 она разделена, в зависимости от того, по генеральной совокупности происходит вычисление или по выборке, на два отдельных варианта: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В.
Синтаксис данных функций выглядит соответствующим образом:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)




Шаг 2: расчет среднего арифметического
Среднее арифметическое является отношением общей суммы всех значений числового ряда к их количеству. Для расчета этого показателя тоже существует отдельная функция – СРЗНАЧ. Вычислим её значение на конкретном примере.




Шаг 3: нахождение коэффициента вариации
Теперь у нас имеются все необходимые данные для того, чтобы непосредственно рассчитать сам коэффициент вариации.



Таким образом мы произвели вычисление коэффициента вариации, ссылаясь на ячейки, в которых уже были рассчитаны стандартное отклонение и среднее арифметическое. Но можно поступить и несколько по-иному, не рассчитывая отдельно данные значения.
-
Выделяем предварительно отформатированную под процентный формат ячейку, в которой будет выведен результат. Прописываем в ней формулу по типу:


Существует условное разграничение. Считается, что если показатель коэффициента вариации менее 33%, то совокупность чисел однородная. В обратном случае её принято характеризовать, как неоднородную.
Как видим, программа Эксель позволяет значительно упростить расчет такого сложного статистического вычисления, как поиск коэффициента вариации. К сожалению, в приложении пока не существует функции, которая высчитывала бы этот показатель в одно действие, но при помощи операторов СТАНДОТКЛОН и СРЗНАЧ эта задача очень упрощается. Таким образом, в Excel её может выполнить даже человек, который не имеет высокого уровня знаний связанных со статистическими закономерностями.
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
- моду
- медиану
- размах ряда
- построить полигон частот
- построить столбчатую и круговую диаграммы
- раскрыть смысловую сторону каждой характеристики
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем – статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические – СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Простая формула для расчета объема выборки
Пример расчета объема выборки
Подставляем эти данные в формулу и считаем:
Получаем объем выборки n = 96 человек.
Задачи о генеральной доле
Пример №1 . С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал , с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет (относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №3 . Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01 ?
Решение ищем по формуле определения численности выборки для повторного отбора.
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01
Пример №4 . Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p Пример №5 . Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
Так как альтернативная гипотеза двусторонняя, то критическое значение статистики K≈ N(0,1) находим по таблице функции Лапласа из равенства
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
По части судить о целом
Читайте также:


