Как сделать радиус на чертеже
Угловые размеры наносят так, как показано на рис.24. Размерная линия проводится в виде дуги с центром в вершине угла, а выносные линии - радиально. Размерное число наносят над размерной дугой со стороны её вогнутости, если размерная линия расположена ниже горизонтальной осевой линии, и со стороны её выпуклости, если она расположена выше горизонтальной осевой линии.
В заштрихованной на рис.24 зоне размеры наносить не рекомендуется, но если этого избежать нельзя, то их следует располагать над горизонтально расположенной полкой линии-выноски. Для углов малых размеров при недостатке места размерное число также наносят над полкой линии-выноски (рис24, угол 10є).
Размерные числа, расположенные над несколькими концентрическими размерными линиями, смещаются в шахматном порядке (рис.25).


Нанесение размеров радиусов показано на рис.26. Перед размерным числом ставится прописная буква R. Знак радиуса и размерное число выполняются шрифтом одного размера. Размерная линия проводится через центр или в направлении центра дуги окружности. Стрелка на такой размерной линии выполняется только на конце, упирающемся в линию дуги. Если необходимо на чертеже указать размер, определяющий положение центра дуги окружности, то через этот центр проводят взаимно перпендикулярные центровые или выносные линии. Размерная линия при этом должна проходить через центр дуги окружности (рис.27).


Если же не требуется указывать размеры, определяющие положение центра дуги окружности, то размерную линию радиуса допускается не доводить до центра и смещать её относительно центра.
При большой величине радиуса, когда центр дуги окружности находится далеко от дуги, допускается приближать центр к дуге на произвольное расстояние, при этом размерную линию проводят с изломом под углом 90є (рис.28).
Если из одного центра проводится несколько размерных линий радиусов дуг, то нужно следить за тем, чтобы две размерные линии не располагались на одной прямой (рис.29).

Рис.28 Рис.29

Радиус - это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
Чертеж радиуса выполняется на основании ГОСТ 2.109-73 - единая система конструкторской документации (ЕСКД).

Вы можете бесплатно скачать этот простой чертеж для использования в любых целях. Например для размещения на шильдике или наклейке.
Как начертить чертеж:
Начертить чертеж можно как на листе бумаги, так и с использованием специализированных программ. Для выполнения простых эскизных чертежей особых инженерных знаний не требуется.
Конструкторский чертеж со всеми технологическими данными для изготовления может выполнить только квалифицированный инженер.
Для обозначения на чертеже необходимо выполнить следующие операции:
1. Начертить изображение;
2. Проставить размеры (см пример);
3. Указать технические требования к изготовлению (подробнее о технических требованиях читайте ниже в статье).
Чертить удобнее всего на компьютере. В последующем чертеж можно распечатать на бумаге на принтере или плоттере. Есть множество специализированных программ для черчения на компьютере. Как платных, так и бесплатных.
Пример черчения:
На этом изображении нарисовано как просто и быстро выполняется чертеж с помощью компьютерных программ.

Список программ для черчения на компьютере:
1. КОМПАС-3D;
2. AutoCAD;
3. NanoCAD;
4. FreeCAD;
5. QCAD.
Изучив принципы черчения в одной из программ не сложно перейти на работу в другой программе. Методы черчения в любой программе принципиально не отличаются друг от друга. Можно сказать что они идентичны и отличаются друг от друга только удобством и наличием дополнительных функций.
Технические требования:
Для чертежа необходимо проставить размеры, достаточные для изготовления, предельные отклонения и шероховатость.
В технических требованиях к чертежу следует указать:
1) Способ изготовления и контроля, если они являются единственными, гарантирующими требуемое качество изделия;
2) Указать определенный технологический прием, гарантирующий обеспечение отдельных технических требований к изделию.
Немного теории:
Чертёж - это проекционное изображение изделия или его элемента, один из видов конструкторских документов содержащий данные для производства и эксплуатации изделия.
Чертеж это не рисунок. Чертеж выполняется по размерам и в масштабе реального изделия (конструкции) или части изделия. Поэтому для выполнения чертежных работ необходима работа инженера, обладающего достаточным опытом в производстве чертежных работ (впрочем для красивого отображения изделия для буклетов вполне возможно понадобится услуга художника, обладающего художественным взглядом на изделие или его часть).
Чертеж - это конструктивное изображение с необходимой и достаточной информацией о габаритах, методе изготовления и эксплуатации. Представленный на этой странице чертеж вы можете скачать бесплатно.
Рисунок - это художественное изображение на плоскости, созданное средствами графики (кисть, карандаш или специализированная программа).
Чертеж может быть как самостоятельным документом, так и частью изделия (конструкции) и технических требований, относящиеся к поверхностям, обрабатываемым совместно. Указания о совместной обработке помещают на всех чертежах, участвующих в совместной обработке изделий.
Подробнее о чертежах, технических требованиях к оформлению и указанию методов изготовления смотрите в ГОСТ 2.109-73. Перечень стандартов для разработки конструкторской документации смотрите здесь.
Информация для заказа чертежей:
В нашей проектной организации Вы можете заказать чертеж любого изделия (как детали, так и сборки), в составе которого будет чертеж радиуса, как элемент конструкторской документации изделия в целом. Наши инженеры-конструкторы разработают документацию в минимальные сроки в точном соответствии с Вашим техническим заданием.

Раздел 3: Чтение и выполнение чертежей (7 часов)
Выполнение чертежей предметов с использованием геометрических построений (деление окружности на равные части, деление углов и отрезков на равные части; сопряжения). Общее понятие о форме и формообразовании предметов. Анализ геометрической формы предметов. Способы чтения и выполнения чертежей на основе анализа формы. Построение третьей проекции предмета по двум заданным. Нахождение на чертеже вершин, ребер и граней, поверхностей геометрических тел, составляющих форму предмета. Определение необходимого и достаточного количества видов на чертеже. Творческие задачи на пройденный материал.
Урок № 11: Деление окружности на равные части

Ботвинников А.Д. § 15.2 [1]
Степакова В. В. § 15 [3]
Вышнепольский И.С. § 8 [8]

При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений.
Деление окружности на равные части с помощью циркуля
Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7, 8, 12 равных участков.
Деление окружности на четыре равные части.
Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 1) .
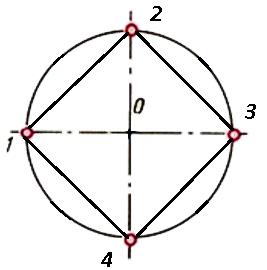
Рис.1 Деление окружности на 4 равные части.
Деление окружности на восемь равных частей.
Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 2).
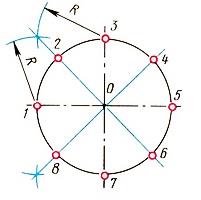
Рис.2. Деление окружности на 8 равных частей.
Деление окружности на шестнадцать равных частей.
Разделив циркулем дугу, равную 1/8, на две равные части, нанесём засечки на окружность. Соединив все засечки, отрезками прямых, получим правильный шестнадцатиугольник.
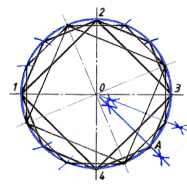
Рис.3. Деление окружности на 16 равных частей.
Деление окружности на три равные части.
Чтобы разделить окружность радиуса R на 3 равные части, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.
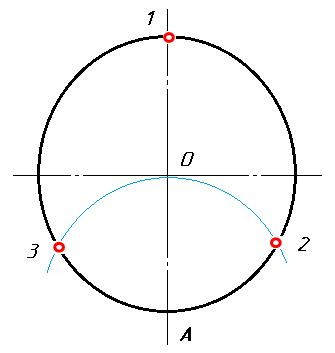
Рис. 4. Деление окружности на 3 равные части.
Деление окружности на шесть равных частей. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности (рис. 5.).
Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.
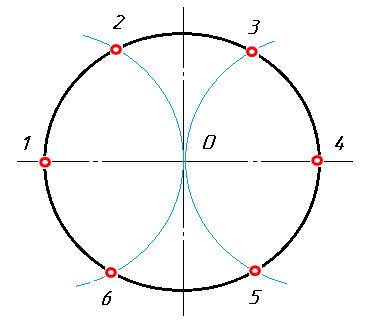
Рис. 5. Деление окружности на 6 равных частей
Деление окружности на двенадцать равных частей.
Чтобы разделить окружность на двенадцать равных частей, надо окружность поделить на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 6).
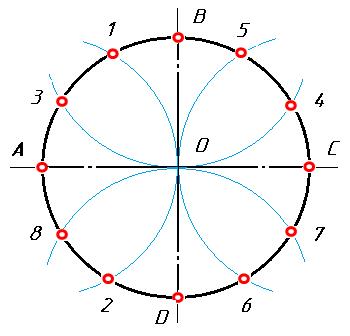
Рис. 6. Деление окружности на 12 равных частей
Деление окружности на пять равных частей
Из точки А проведем дугу тем же радиусом, что и радиус окружности до пересечения с окружностью – получим точку В. Опустив перпендикуляр с этой точки – получим точку С. Из точки С – середины радиуса окружности, как из центра, дугой радиуса СD сделаем засечку на диаметре, получим точку Е. Отрезок DЕ равен длине стороны вписанного правильного пятиугольника. Сделав радиусом DЕ засечки на окружности, получим точки деления окружности на пять равных частей.
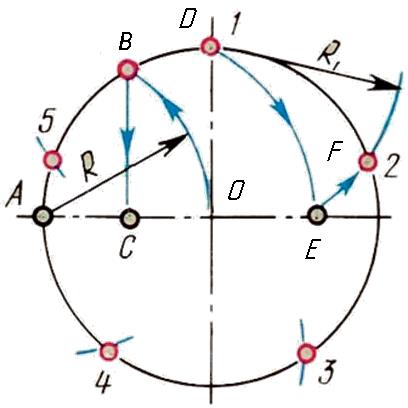
Рис. 7. Деление окружности на 5 равных частей
Деление окружности на десять равных частей
Разделив окружность на пять равных частей, легко можно разделить окружность и на 10 равных частей. Проведя прямые от получившихся точек через центр окружности до противоположных сторон окружности – получим ещё 5 точек.
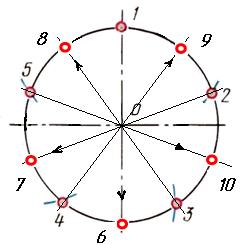
Рис. 8. Деление окружности на 10 равных частей
Деление окружности на семь равных частей
Чтобы разделить окружность радиуса R на 7 равных частей, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу этим же радиусом R – получают точку В. Опустив перпендикуляр с точки В – получим точку С. Отрезок ВС равен длине стороны вписанного правильного семиугольника.
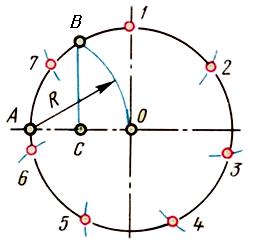
Рис. 9. Деление окружности на 7 равных частей

Практические задания, тесты и домашние работы
Графическая работа

Вопросы для повторения


Домашняя работа
Понятно, что одних лишь линейных размеров недостаточно для получения полного представления об изделии. Даже в случае такого простого объекта, как рабочая зона, необходимо использовать угловые размеры, а также радиусы и диаметры.
2. В ответ на предложение AutoCAD выбрать объект, для которого нужно показать угловой размер, щелкните на линии, соединяющей два сопряжения в угловой части рабочей зоны (рис. 11.22).

Рис. 11.22 Выбор первой линии углового размера
3. AutoCAD предложит выбрать вторую линию. Выберите горизонтальную линию, представляющую нижнюю границу контура прямолинейной части столешницы. AutoCAD создаст угловой размер, вид и размерное число которого будет зависеть от расположения указателя-перекрестия (рис. 11.23).

Рис. 11.23 Выбор расположения углового размера
Выберите оптимальное размещение размера и щелкните для его создания.
5. В ответ на приглашение AutoCAD выбрать дугу или окружность щелкните на сопряженном участке угловой части столешницы, как показано на рис. 11.24.

Рис. 11.24 Выбор объекта для нанесения размера радиуса
6. Выберите место расположения радиуса и щелкните для создания соответствующего размера.
8. AutoCAD предложит выбрать дугу или окружность. Щелкните на окружности, которая представляет на чертеже наружный контур монтажного кольца основной опоры, а затем задайте оптимальное расположение созданного обозначения диаметра (рис. 11.25).

Рис. 11.25 На чертеже показан диаметр монтажного кольца основной опоры
Совет. Для того чтобы изменить расположение размерного числа, можно использовать перетаскивание маркера этого числа, который появляется после щелчка на размерном объекте.
Таким образом, создание угловых размеров, а также радиусов и диаметров – задача, в общем-то, несложная. Попрактикуйтесь в выполнении соответствующих операций, руководствуясь рис. 11.26.

Рис. 11.26 Чертеж с нанесенными радиусами, диаметрами и угловыми размерами
Для комфортного просмотра не забудьте переключить качество на более высокое в плеере youtube.
Если есть вопросы или пожелания, обязательно пишите их в комментариях, ставьте лайки, делитесь этим видео в соц. сетях и мы будем чаще радовать Вас новыми уроками!
Нанесение размеров в Автокаде. Основные команды
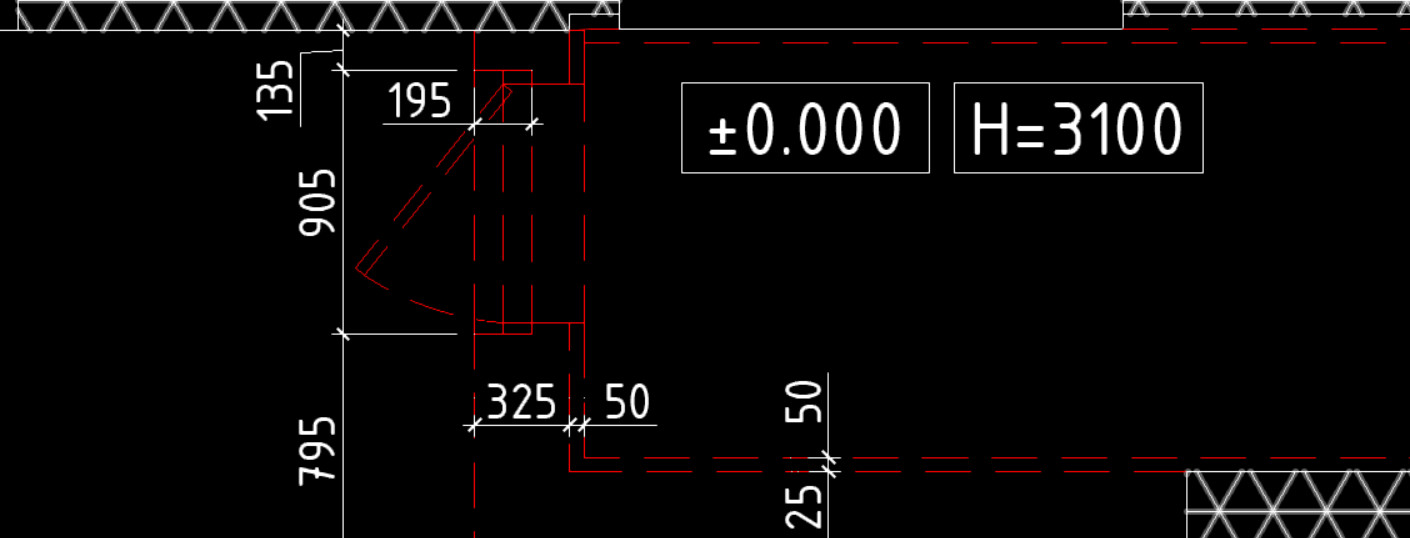
Про то, как вынести размеры в Автокаде, мы говорили ранее. Было рассмотрено несколько способов изменения масштаба размеров и его элементов. В предыдущей статье речь шла про настройку размерного стиля в соответствии с ГОСТ.
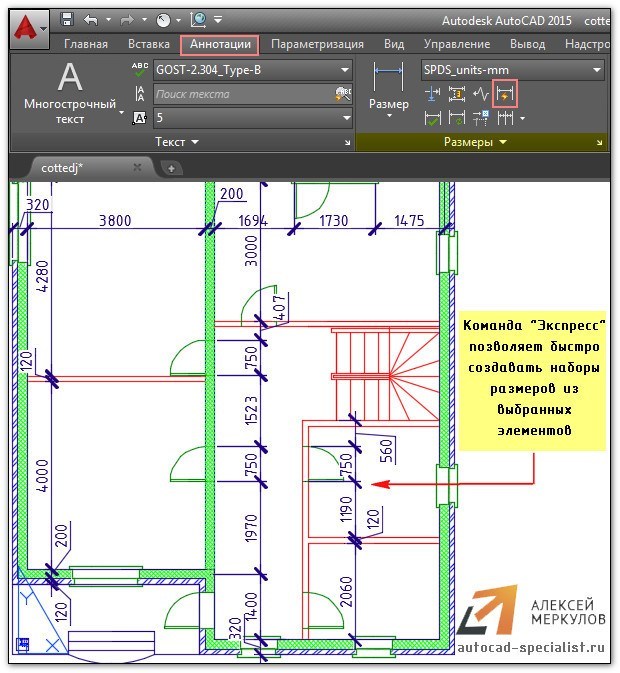
Чтобы выполнить команду, нужно выделить сразу несколько объектов и указать местоположение размера. В проставленном размере отображаются расстояния между всеми выделенными точками. К контекстным свойствам относится:
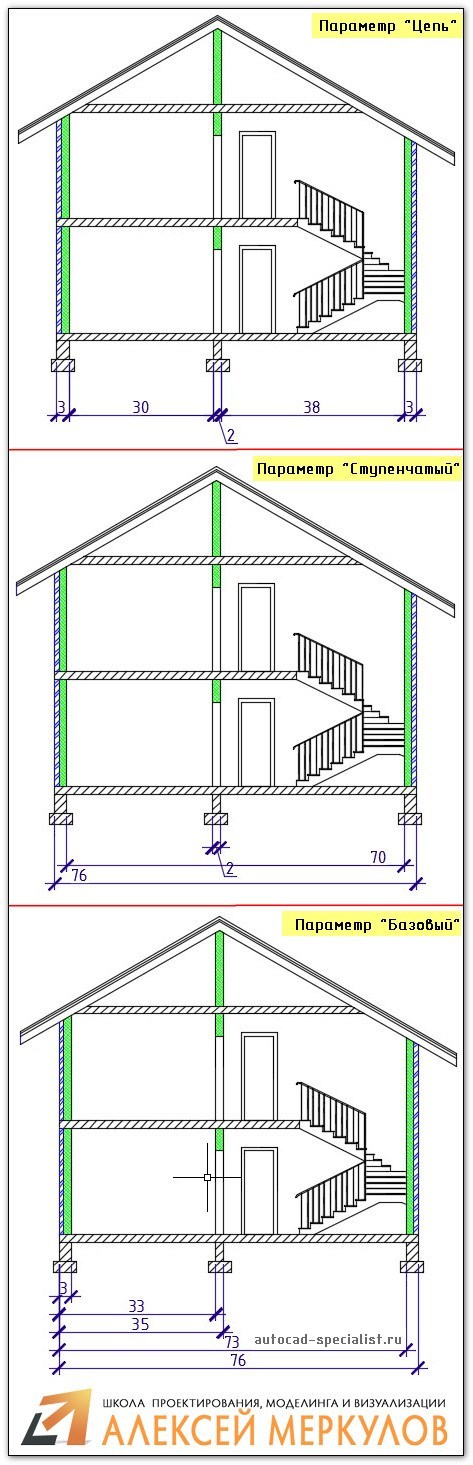
Чтобы поставить цепь размеров вручную, нужно:
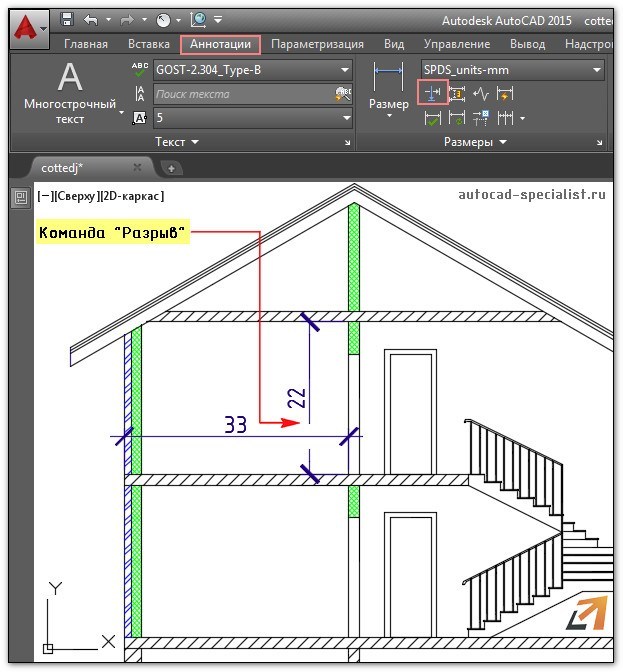
Рис. 3. Разрыв размера в AutoCAD.
Свойство ассоциативности подразумевает, что объекты (в данном случае размеры) взаимосвязаны с исходными элементами чертежа, которые нужно образмерить (отрезки, дуги и т.д.). При изменении длины отрезка, значение текста в размере автоматически пересчитывается. Возможно, вы сталкивались с тем, что на чертеже появляются восклицательные знаки, как на рис. 4. Это значит, что ассоциативность между размером и объектом была утеряна.
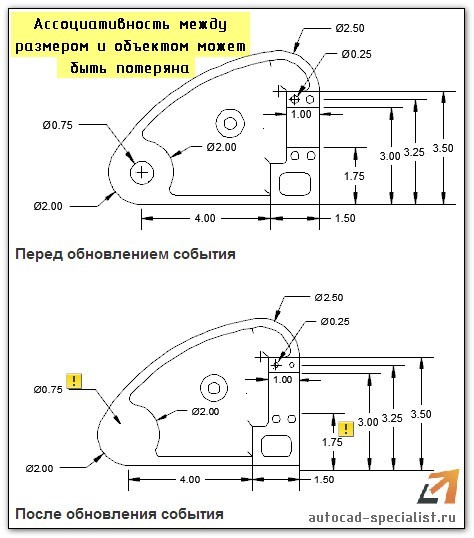
Рис. 4. Свойство ассоциативности размеров в AutoCAD.
Вы всегда можете воспользоваться справкой Autodesk (горячая клавиша F1), если возникнут трудности.
Несколько слов про размеры в Автокаде 3d
Размеры всегда проставляются в плоскости XY. Если возникает необходимость вынести размер, к примеру, высоту объемного объекта, т.е. по оси Z, то у вас ничего не получится. Чтобы выполнить данную операцию, достаточно переопределить направление осей, работать в Пользовательской системе координат.

Рис. 5. Размеры в Автокаде 3д.
Читайте также:


