Как сделать прямоугольник по математике
Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.
Основные геометрические фигуры:
Двухмерные плоские фигуры
Трехмерные фигуры, у которых есть объем
Абсолютно все предметы в основе своего построения имеют эти фигуры.
Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина. В самом кубе заложено понятие рисунка в целом.
Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы. Для большего понимания и анализа рисунка есть несколько упражнений.
Упражнения
Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет). Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.
Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…

Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов. Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Чтобы нам чувствовать пространство, нужно придать рисунку плавности. То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.
Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке.
Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.
Или дневник начинающего художника
![]()

Продолжаю рассказывать об упражнениях, улучшающих навык рисования, в данном случае геометрических фигур. Будем тренироваться рисовать их двухмерное отображение, трехмерное отображение и затенение фигур. Итак, Упражнения для рисования. Часть 2. Приступим.
Но прежде, чем приступить к упражнениям, напоминаю, что есть первая часть упражнений, посвященная линиям и штрихам.
Двумерные фигуры


Треугольник. Пробуем нарисовать равносторонний треугольник. Опять же, чтобы себе помочь для начала можем нарисовать окружность с помощью циркуля и уже в нее вписать нашу фигуру. Но потом обязательно пробуем нарисовать самостоятельно.

Квадрат. Да, сложно с первого раза нарисовать все стороны одинаковыми и все углы 90 градусов. Поэтому, чтобы запомнить правильную форму используем линейку. Потом рисуем по точкам, а потом самостоятельно, без вспомогательных инструментов.

После квадрата рисуем ромб, то есть тот же квадрат, но повернутый на 45 градусов.

Рисуем 5-конечную звезду, рисуем не отрывая карандаш от бумаги. Для первого раза можно воспользоваться циркулем и вписать звезду в окружность, чтобы добиться симметрии.

Шестиконечная звезда. Рисуется как 2 равносторонних треугольника.

Восьмиконечная звезда. Рисуется как 2 квадрата.

Яйцо. Это овал, который на одном конце уже, чем на другом.

Полумесяц. Эту фигуру нарисовать не так просто, как может показаться на первый взгляд. Сначала попробуйте нарисовать его самостоятельно, а потом уже при помощи циркуля, помня, что месяц это фактически часть двух пересекающихся окружностей.
Трехмерные фигуры


Переходим к трехмерным фигурам. Начнем с куба. Рисуем квадрат, потом еще один квадрат чуть выше и правее, соединяем углы ровными линиями. Получаем прозрачный куб. Теперь попробуем нарисовать тот же куб, но уже без видимых линий внутри.


Теперь рисуем куб в другом ракурсе. Для этого сначала рисуем плоский параллелограмм в форме ромба, опускаем них перпендикуляры и рисуем такую же фигуру в основании. И такой же куб, но без видимых линий.



Теперь попробуем нарисовать цилиндр в разных ракурсах. Первый цилиндр будет прозрачный, рисуем овал, опускаем вертикали вниз и рисуем овал-основание. Затем рисуем цилиндр с невидимой нижней внутренней гранью и цилиндр с невидимой верхней внутренней гранью.
И завершаем этот цикл фигур рисованием конуса в разных ракурсах.
Трехмерные фигуры и тени

Рисуем круг. Намечаем легкой штриховкой тень в левом нижнем углу. Тень должна быть в форме полумесяца. Далее добавляем тона в тень при помощи большего нажима на карандаш, затеняем от центра к краю по принципу от светлого к темному, при этом у границы круга оставляем небольшой участок более светлой тени, это рефлекс. Дальше затеняем падающую тень, чем дальше от основания шара, тем светлее. Тень находится с противоположной от источника света стороны. То есть в нашем случае источник света находится в верхнем правом углу.

Теперь затеняем куб. В данном случае свет также находится в верхнем правом углу, а значит самая темная тень будет с противоположной стороны, сверху тени не будет, а правая видимая грань будет иметь более светлый тон. Соответственно с этим и наносим штриховку.


По такому же принципу затеняем стороны на кубе и конусе, важно следить за формой объекта и тем, как на него ложится свет. И падающая тень также должна соответствовать форме объекта.
И еще, в упражнениях для затенения используется диагональная штриховка, но я бы советовала пробовать в дальнейшем штриховать по форме объекта, тогда объект будет более объемный. Но штриховка по форме, да и вообще штриховка — тема довольно обширная, я уже начала ее изучать и скажу, что без тренировки рук и ровного быстрого штриха тут никуда, так что даже если делать только то, что я уже выложила, делать регулярно, то рисунки неизбежно будут становиться все лучше.
Способы построения изометрической проекции плоских фигур, геометрических тел и деталей
Для выполнения изометрической проекции любой детали необходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.
Правила построения изометрических проекций геометрических фигур. Построение любой плоской фигуры следует начинать с проведения осей изометрических проекций.
При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе стороны половину длины стороны квадрата. Через полученные засечки проводят прямые, параллельные осям.
При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные засечки отрезками прямых.
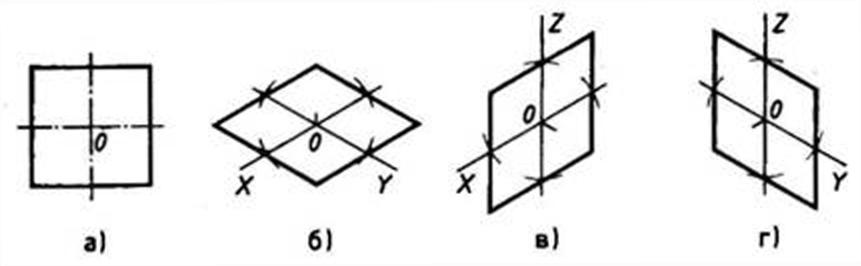
Рис. 109. Прямоугольная и изометрические проекции квадрата
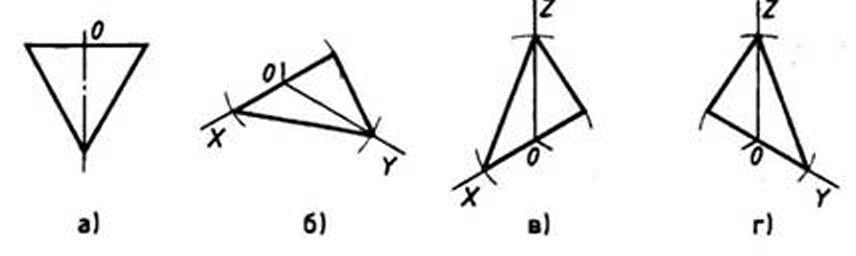
Рис. 110. Прямоугольная и изометрические проекции треугольника
При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе стороны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Соединяют полученные засечки отрезками прямых.
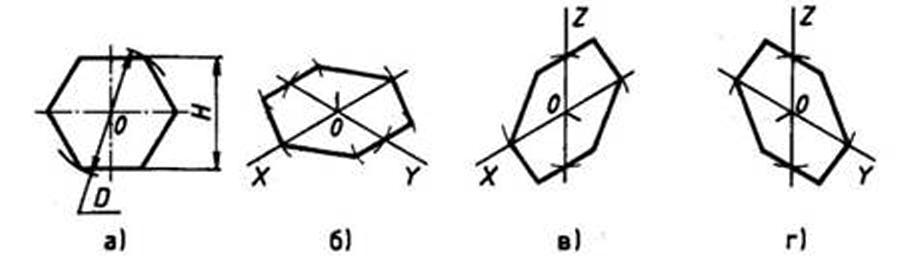
Рис. 111. Прямоугольная и изометрические проекции шестиугольника
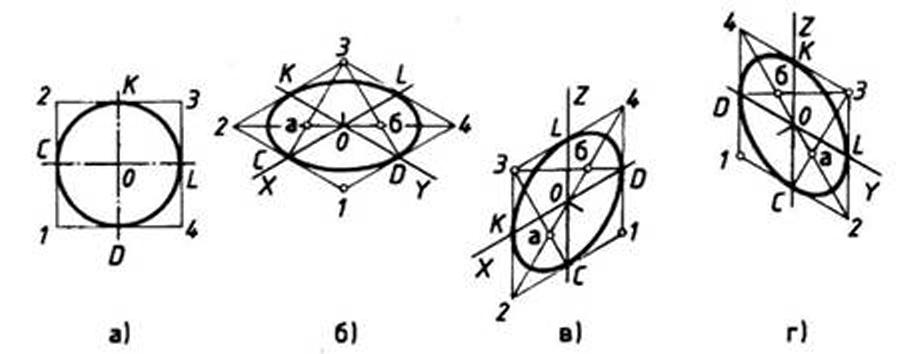
Рис. 112. Прямоугольная и изометрические проекции круга
При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, параллельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заменяющий аксонометрическую проекцию круга.
Используя описанные построения, можно выполнить аксонометрические проекции простых геометрических тел (табл. 10).
10. Изометрические проекции простых геометрических тел
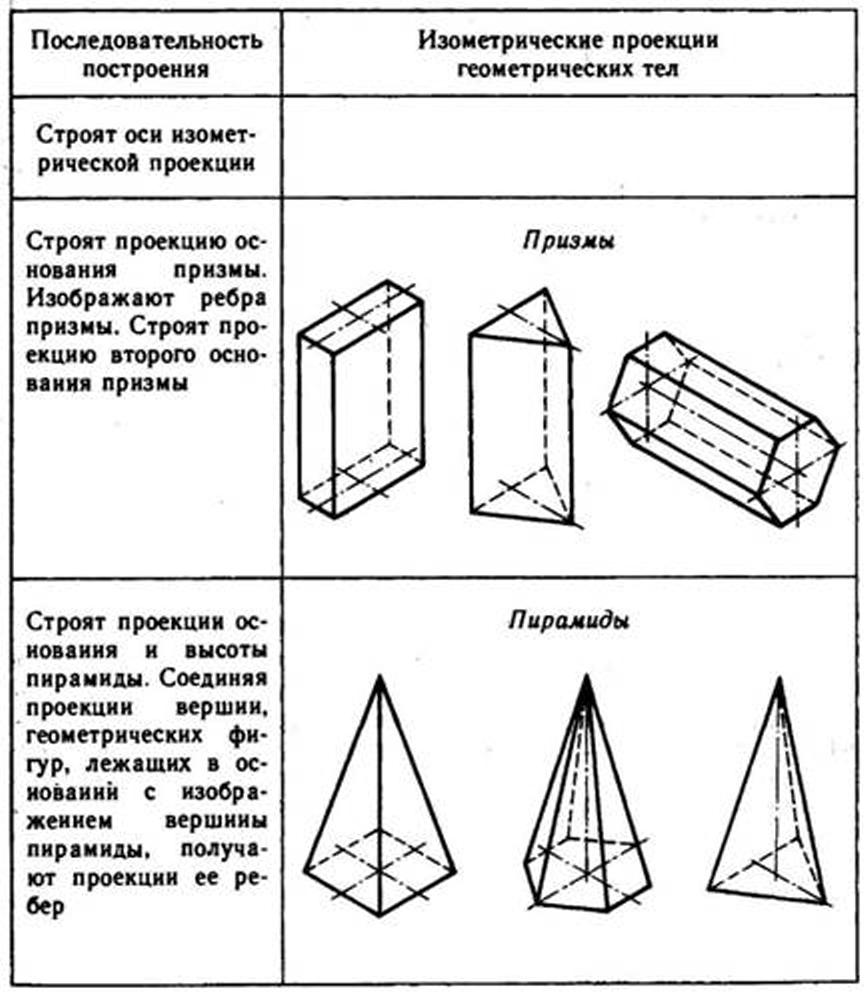
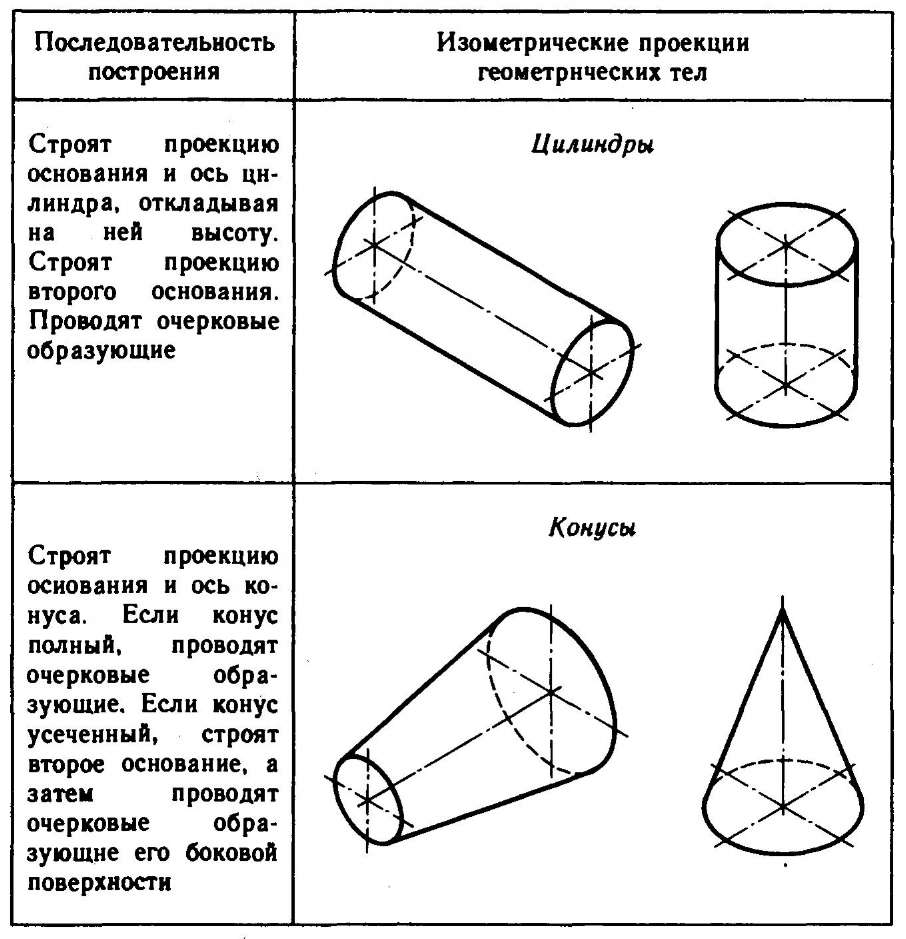
Способы построения изометрической проекции детали:
1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма которых имеет плоскую грань, называемую формообразующей; ширина (толщина) детали на всем протяжении одинакова, на боковых поверхностях отсутствуют пазы, отверстия и другие элементы. Последовательность построения изометрической проекции заключается в следующем:
1) построение осей изометрической проекции;
2) построение изометрической проекции формообразующей грани;
3) построение проекций остальных граней посредством изображения ребер модели;
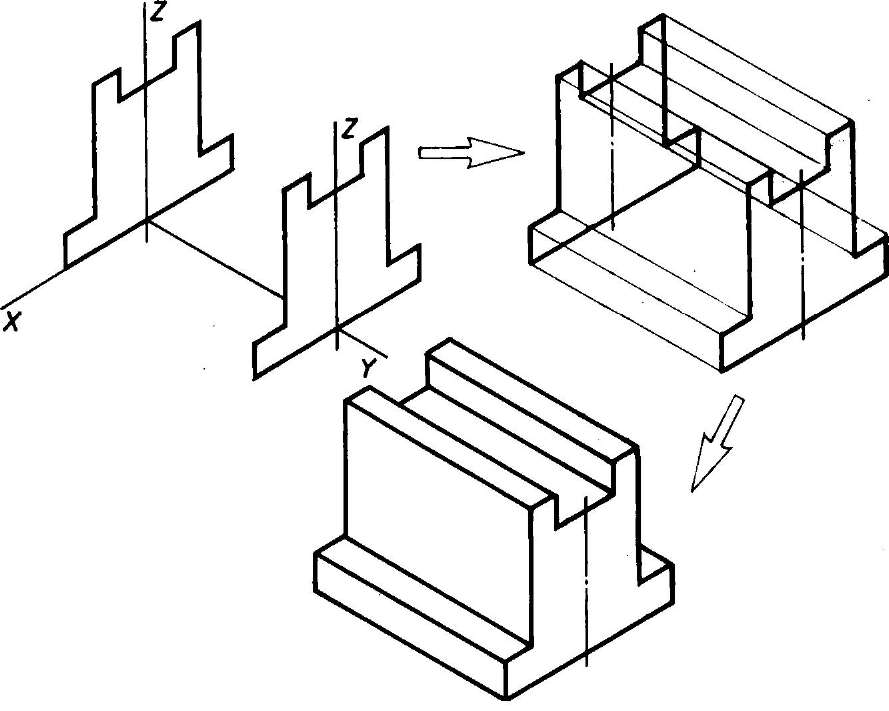
Рис. 113. Построение изометрической проекции детали, начиная от формообразующей грани
4) обводка изометрической проекции (рис. 113).
- Способ построения изометрической проекции на основе последовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
- Способ построения изометрической проекции на основе последовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных определенным образом друг с другом (рис. 115).
- Комбинированный способ построения изометрической проекции. Изометрическую проекцию детали, форма которой получена в результате сочетания различных способов формообразования, выполняют, используя комбинированный способ построения (рис. 116).
Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) невидимых частей формы.
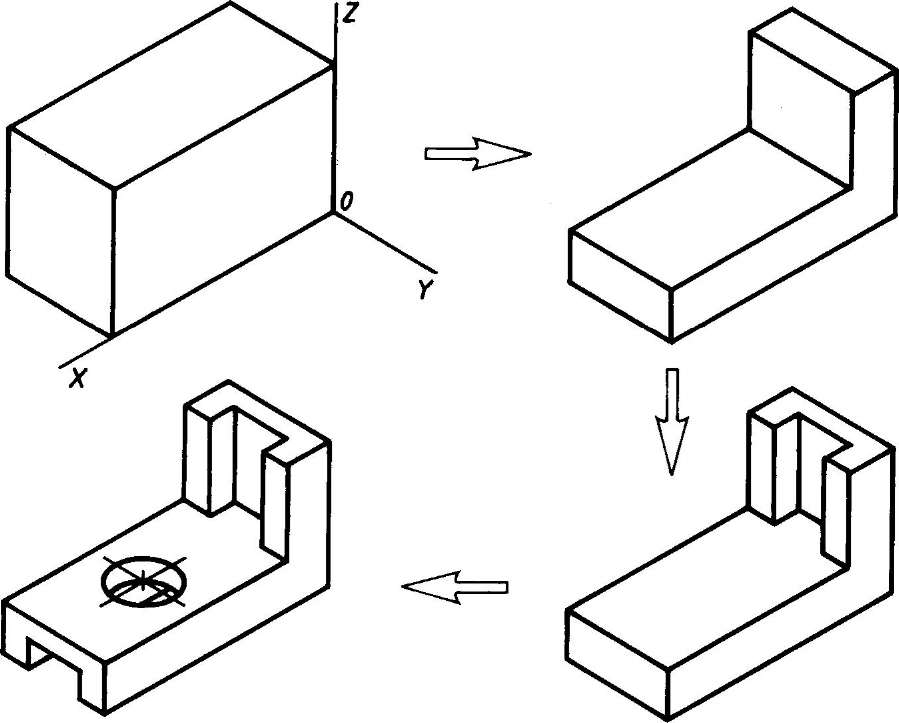
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов
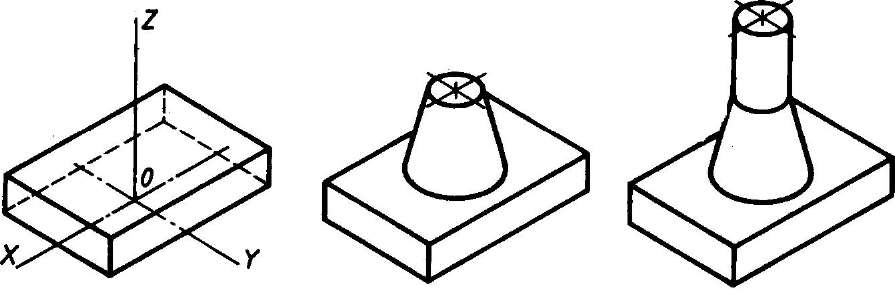
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов
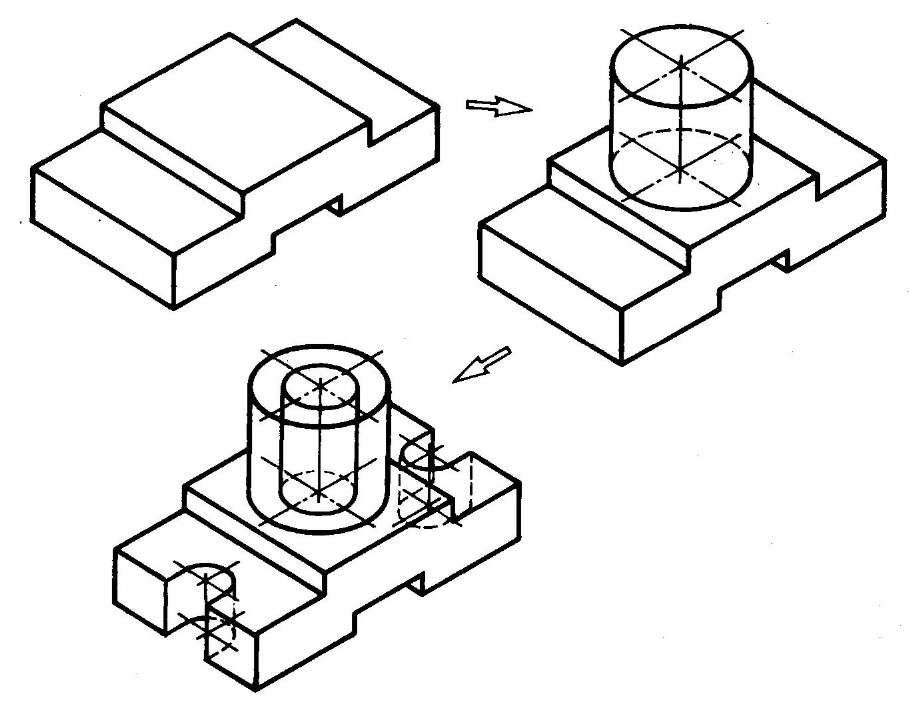
Рис. 116. Использование комбинированного способа построения изометрической проекции детали
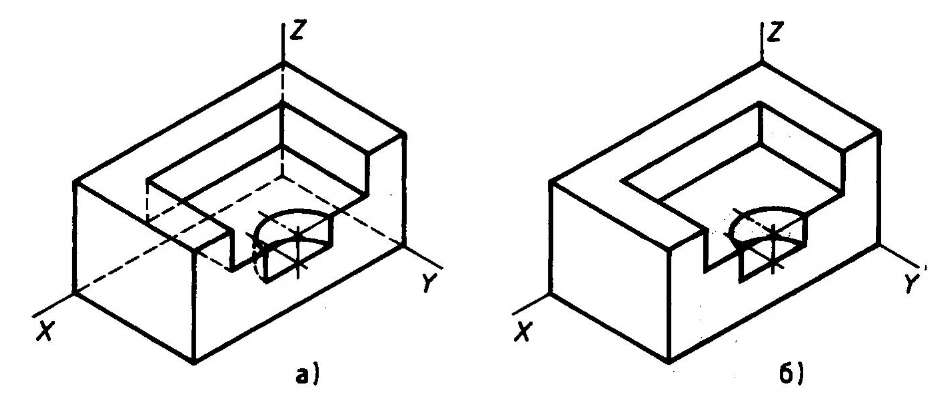
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Перспективная цель: создание организационных и содержательных условий для углубления знаний о прямоугольниках в ходе смены видов деятельности.
Актуальная цель: создание условий для формирования знаний построения прямоугольников на нелинованной бумаге в ходе смены видов деятельности
Образовательная: учить строить прямоугольники с помощью треугольника на нелинованной бумаге в ходе выполнения заданий.
Развивающая: развивать пространственное воображение при построении прямоугольников на нелинованной бумаге.
Воспитывающая: воспитывать ответственность в ходе решения заданий.
Планируемые результаты:
Предметные: знают алгоритм построения прямоугольников на нелинованной бумаге
Личностные: осознают свои пробелы в знаниях и ставят цель узнать больше
Метапредметные: Регулятивные: учатся работать по алгоритму
Познавательные: узнают, как построить прямоугольник на нелинованной бумаге
Коммуникативные: учатся оформлять свои мысли при решении задний
Оборудование: учебник, рабочая тетрадь
Тип урока: УCНЗ
Вид урока: урок-практикум
Принципы: психологической комфортности, деятельности, непрерывности, целостности, минимакса, вариативности.
Методы: Объяснительно-иллюстративный, репродуктивный
Литература: Рудницкая. Математика. 4 кл. Учебник, рабочая тетрадь
Этапы урока
Деятельность учителя
Деятельность
Планируемые результаты
(предметные, метапредметные, личностные)
1.Организационно - мотивационный
- Здравствуйте дети! Прозвенел звонок, начинается урок, очень тихо
вы садитесь, и работать не ленитесь!
Послушайте и угадайте, что это?
Эта фигура синего цвета из толстого картона, плоская, имеет четыре прямых угла и четыре стороны, так же противоположные стороны равны
Что вы знаете о прямоугольниках? Назовите существенные признаки.
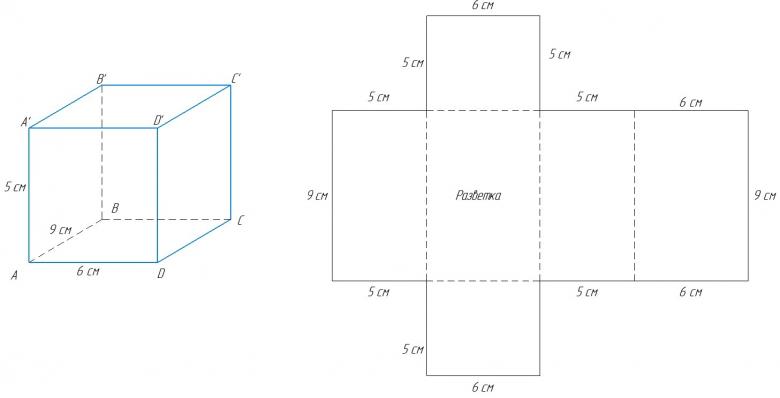
1.Построите вам прямоугольник со сторонами 9см и 5 см
А теперь проверим, насколько вы точно начертили прямоугольник. Я выдам вам заготовку, а вы проверите с помощью наложения точность построения.
У всех получилось?
В связи с этим, цель нашего урока научиться правильно строить прямоугольники на нелинованной бумаге.
Дети слушают учителя.
Подготавливаются к уроку.
Прямоугольник – это геометрическая фигура. У прямоугольника четыре прямых угла, противоположные стороны равны
Строят прямоугольник на нелинованной бумаге
Проверяют свои чертежи
Нет, у некоторых прямоугольник получился кривой.
Коммуникативные УУД:
развитие произвольного внимания
Предметные УУД:
Выделяют главные признаки прямоугольника
Личностные УУД:
Осознают цель урока
2. Открытие новых знаний и способов деятельности.
Расскажите, как вы строили прямоугольник
Давайте рассмотрим алгоритм в учебнике на стр 47. Расскажите, как построили прямоугольник волк и заяц
2.Теперь пользуясь этим алгоритмом, на обратной стороне листа постройте прямоугольник со сторонами 3 см и 7 см. Так же проверим способом наложения
Давайте подведем итог. Для того, что бы построить прямоугольник не нелинованной бумаге надо…
Рассказывают алгоритм действий
Строятся два луча, по прямому углу в угольнике. На этих лучах откладываются нужные отрезки. Затем снова используя прямой угол угольника, достраиваются остальные две стороны.
Получилось построить ровный прямоугольник на нелинованной бумаге
Построить прямой угол по треугольнику, на его лучах отмерить нужные отрезки, затем прикладывая одну сторону прямого угла треугольника дочертить недостающие сторону прямоугольника.
Познавательные УУД
Развитие умения добывать новые знания: извлекать информацию, представленную в форме иллюстраций
Коммуникативные УУД
Развивают умение доносить свою позицию до других: оформлять свои мысли в устной речи
Личностные результаты
в созданных совместно с педагогом на уроке ситуациях общения и сотрудничества, опираясь на общие для всех простые правила поведения, делать выбор, как себя вести. Познавательные УУД
перерабатывать полученную информацию: сравнивать и группировать математические факты и объекты;
делать выводы на основе обобщения умозаключений;
преобразовывать информацию из одной формы в другую;
3.Самостоятельное применение новых знаний
Ответьте верно ли утверждения: все квадраты – это прямоугольники и все прямоугольники - это квадраты. Почему?
Как можно построить квадрат на нелинованной бумаге?
Постройте квадрат со стороной 5 см
Давайте решим задачу.
Периметр квадрата 14 см 2 . Начертите этот квадрат.
Какой алгоритм построения будет?
Проверяем себя. Выполните задание в рабочей тетради на стр 22 №75
Верно утверждение: все квадраты – прямоугольники, потому что у квадрата так же как и у прямоугольника все четыре угла прямые, но так же все стороны равны. А прямоугольника соседние стороны могут быть не равны, поэтому не все квадраты – прямоугольники.
Так же как и прямоугольник, только стороны будут равны
Для начала надо найти сколько см одна сторона:
14:2 =7см – две стороны
7:2=3.5см – одна сторона квадрата
Строим квадрат по алгоритму
Регулятивные УУД
Развивают умения:
составлять план решения отдельной учебной задачи;
сверять свои действия с целью и при необходимости исправлять ошибки с помощью класса;
в диалоге с учителем и другими учащимися учиться вырабатывать критерии оценки и определять степень успешности выполнения своей работы и работы всех, исходя из имеющихся критериев.
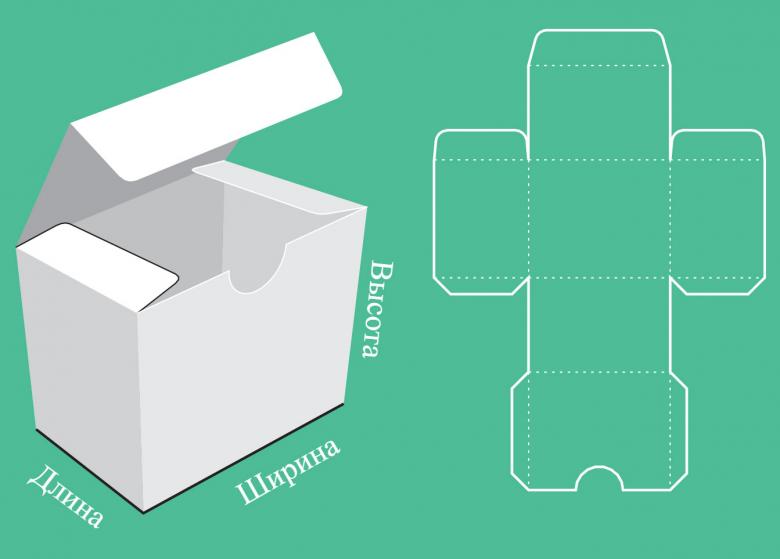
Как создать прямоугольник параллелепипед своими рукамиНаверняка многие из вас делали для разнообразных проектов подделки на тему геометрических фигур. Простейшей из моделей может стать самый обыкновенный параллелепипед, который мы часто видим в виде простой коробки.Для создания геометрических фигур нужно немного творческого воображения, доступные материалы и конечно же – шаблон, по которому будет сделана модель.

Что может понадобиться в работе?
Для начала следует определиться с набором материалов и для каких целей будет изготавливаться модель. Далее мы рассмотрим на конкретном примере как сделать параллелепипед из бумаги.

Для работы нужно подготовить:
- Клей,
- Бумагу,
- Картон,
- Ножницы,
- Ручку,
- Линейку,
- Карандаш.
- Модель параллелепипеда

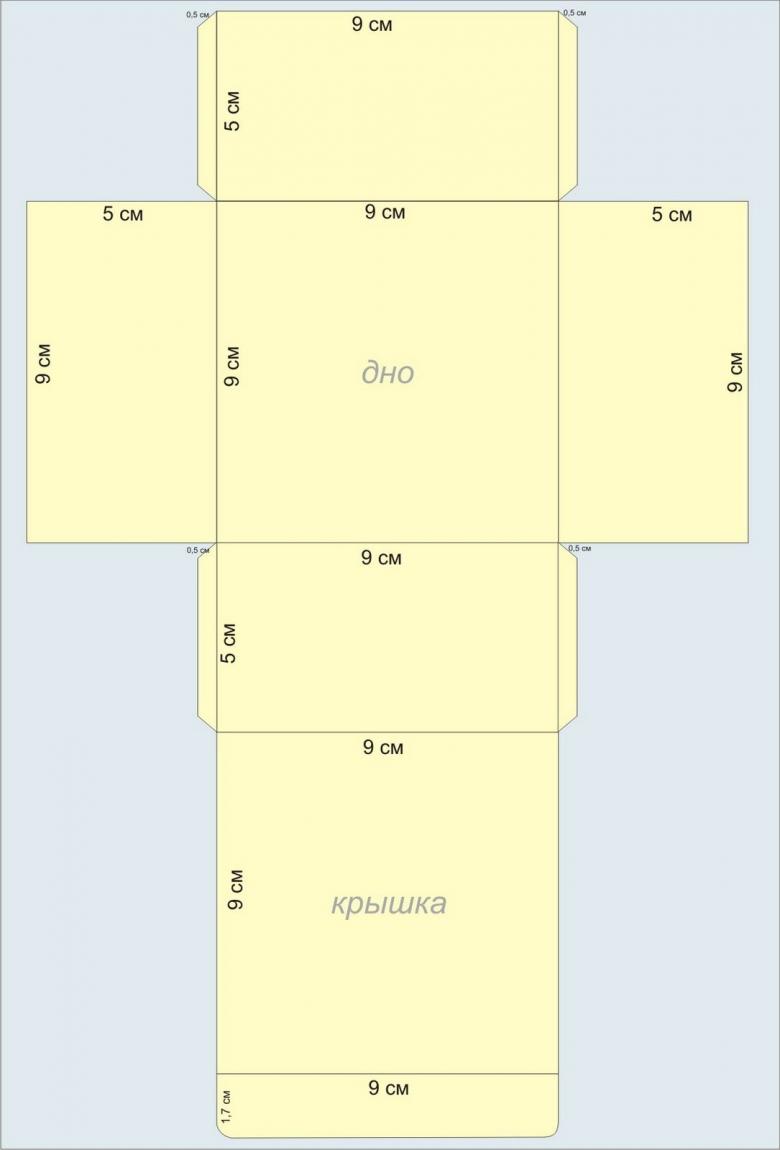
Как сделать параллелепипед из бумаги схема
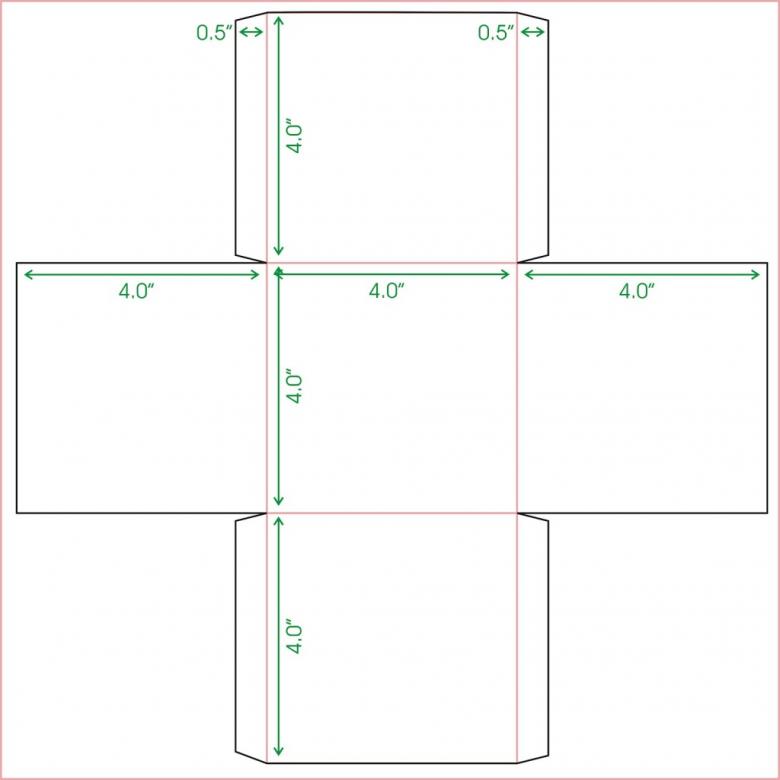
Для изготовления будет рассмотрена базовая модель. Как вы видите, шаблон полностью пропорционален своим сторонам и имеет контуры для загиба и склеивания модели по швам.
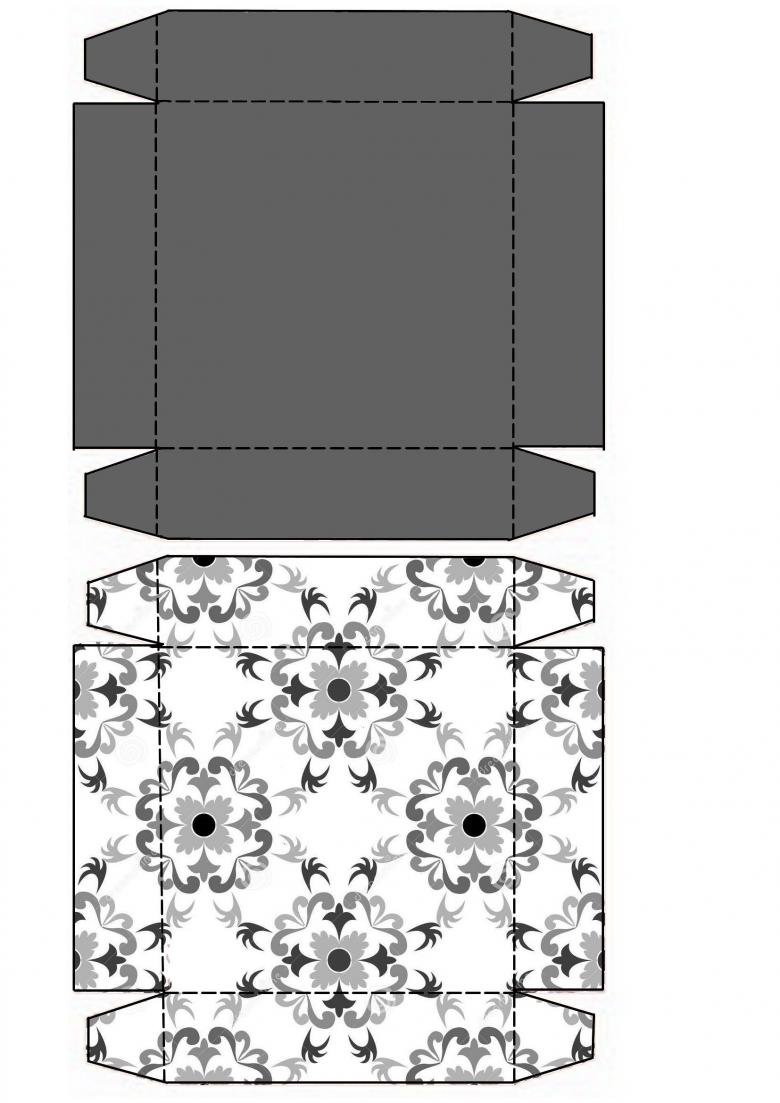

Основная сторона полностью пропорциональна своей стороне на параллели, а это значит, что соседние грани должны тоже быть параллельно пропорциональны друг другу. Чтобы не усложнять процесс, достаточно просто распечатать готовый шаблон и вырезать его по нужным линиям. Обратите внимание, что для уровня склейки боковые грани обозначены другим цветом.
Важные моменты
Многие задаются вопросом, как сделать прямоугольный параллелепипед равномерным? В этом вопросе хорошо поможет карандаш и линейка, так как главное соблюдать пропорции размеров. Если их не будет, модель попросту не получиться, а если сделать все стороны одинаковыми, тогда у нас получиться не параллелепипед, а квадрат.

Где еще можно применить модель прямоугольника в быту и подделках?На одной только геометрии не сошелся мир, ведь в этом деле можно проявить фантазию, после чего простая и скучная модель превращается в настоящую красочную подделку.
Идеи для творчества
Фотографии на прямоугольнике
Хотите добавить оригинальности собственным фотографиям? Тогда, почему бы их не сделать в рамку из параллелепипеда? Благодаря этой незамудренной модели вы сможете постоянно менять фотографии на любимой полке всего лишь перевернув вам прямоугольник на новую грань.

Что для изготовления понадобиться?
- Шаг 1 – Берем плотную бумагу или картон для изготовления модели.
- Шаг 2 – Наносим на картон шаблон параллелепипеда.
- Шаг 3 – Готовый шаблон следует наметить по расположению фотографий.
- Шаг 4 – Сделайте обрезку фотографий.
- Шаг 5 – Вырезайте готовый шаблон прямоугольника.
- Шаг 6 – Склейте модель за схемой по граням.
- Шаг 7 – После высыхания нанесите клей на грани.
- Шаг 8 – Приклейте поочередно фотографии с намеченным расположением.
- Шаг 9 – Дайте конструкции высохнуть.
- Шаг 10 – Все, модель готова к использованию.
По желанию можно покрыть модель прямоугольника скотчем, что обеспечит большую долговечность и сохранность.
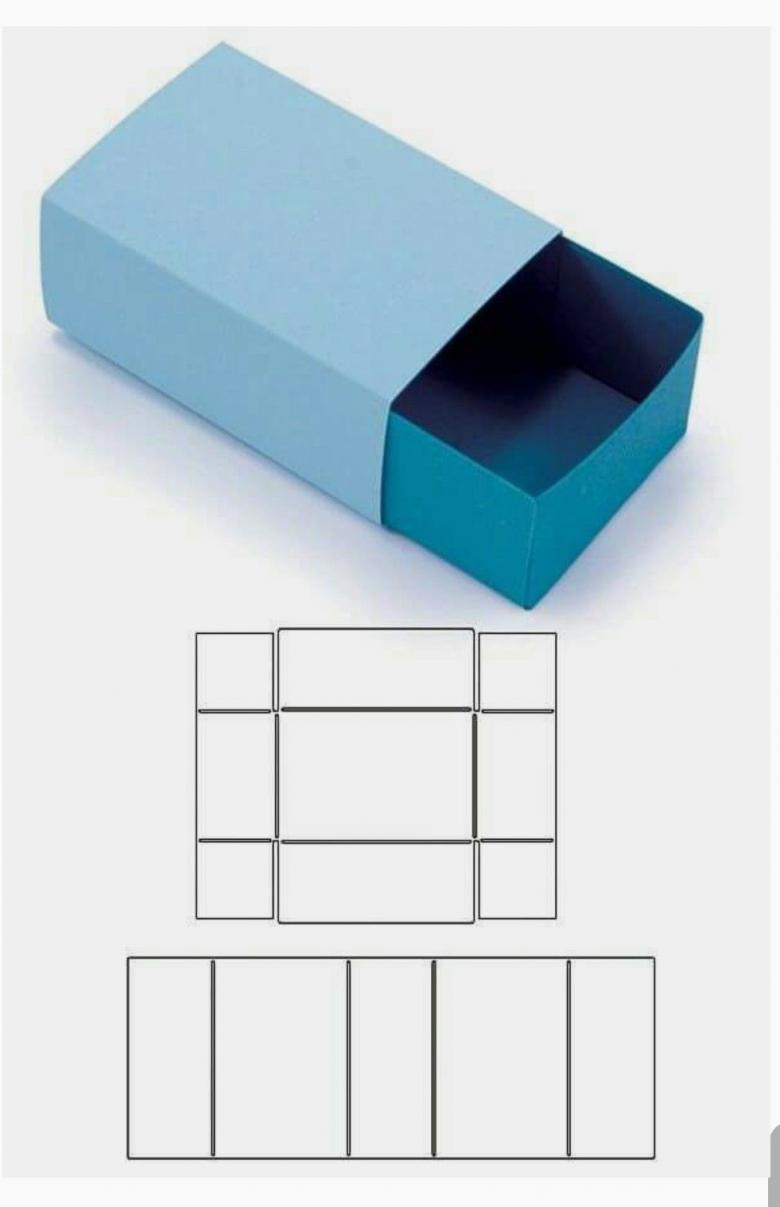
Коробочка на подарок
Сделать прямоугольную коробочку своими руками не так уж и сложно. Все что вам нужно, это придерживаться того же шаблона и пропорций. Единственное отличие, вам нужно не заклеивать плотно все стороны. Это нужно для того, чтобы готовую модель можно было использовать как коробку для подарка.


Ромбический параллелепипед
Еще один оригинальный вариант создания прямоугольника может стать основа ромба. Кроме своей необычной формы этот вариант отлично подойдет на оформления подарка или какой-то подделки.Основная схема имеет в своей основе не прямоугольники, а ромбы, которые мы видим на готовой схеме.
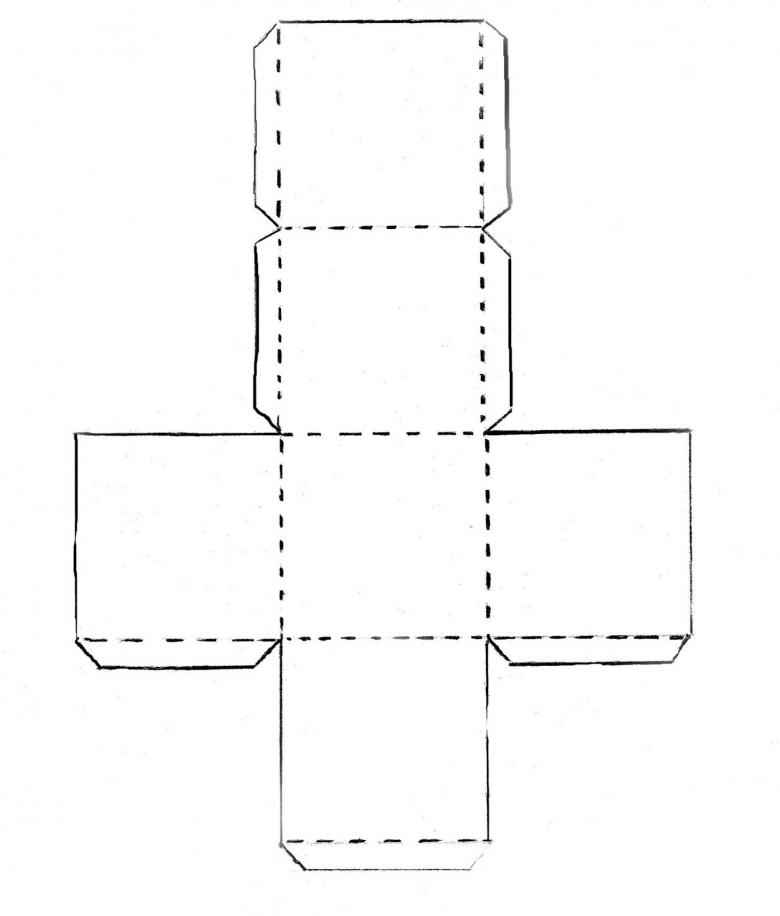
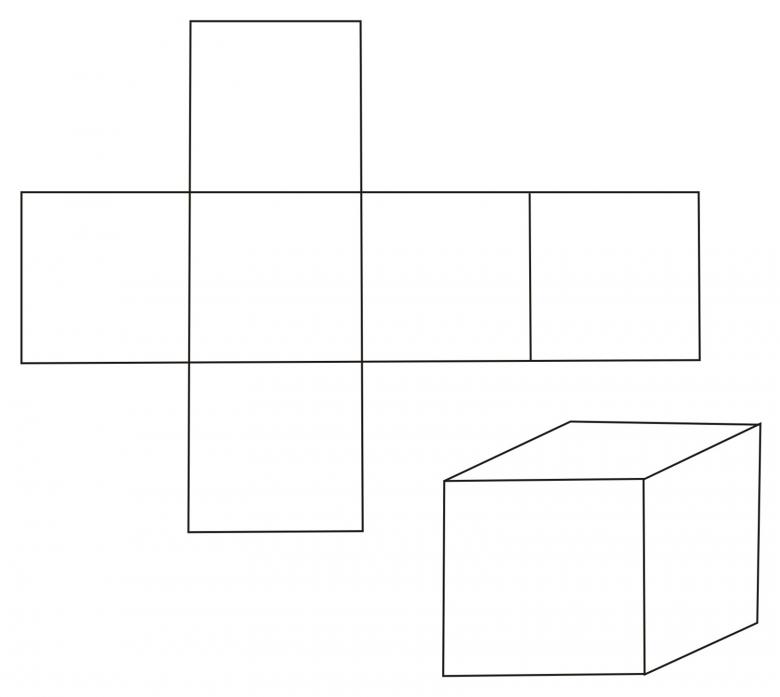
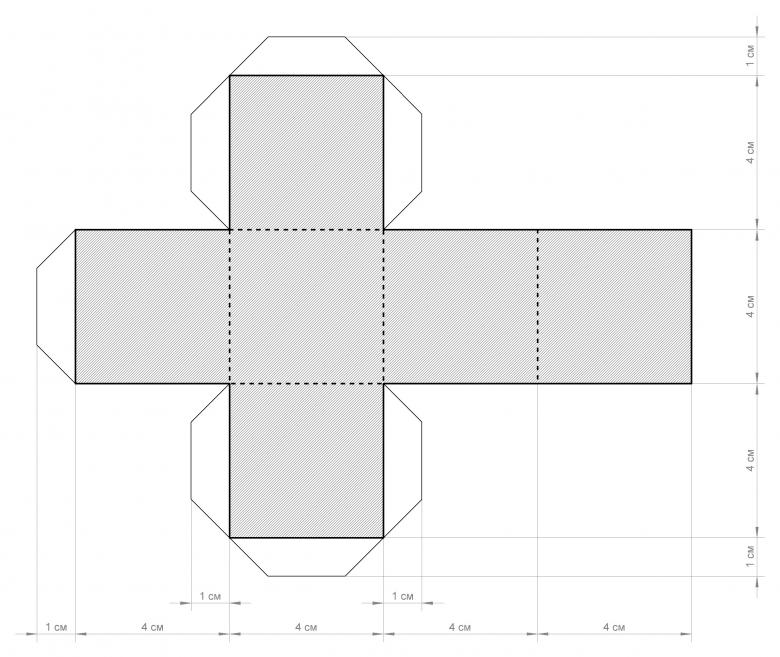
ВАЖНО! Не забывайте о технике безопасности работы с клеем, ножницами и другими материалами. Если вы готовите модель объемного параллелепипеда/прямоугольника, тогда рекомендуем вам проконсультировать детей в правильности использования материалов и инструментов, с которыми они работают. Объясните правила склейки и с какой стороны нужно загибать грани.
Параллелепипед школьникам
Довольно часто на уроках школьникам могут задавать создание разнообразных геометрических фигур, и прямоугольник – одна из них. Само по себе фигура является довольно простой, однако, многие испытывают трудности на этапе сборки модели.
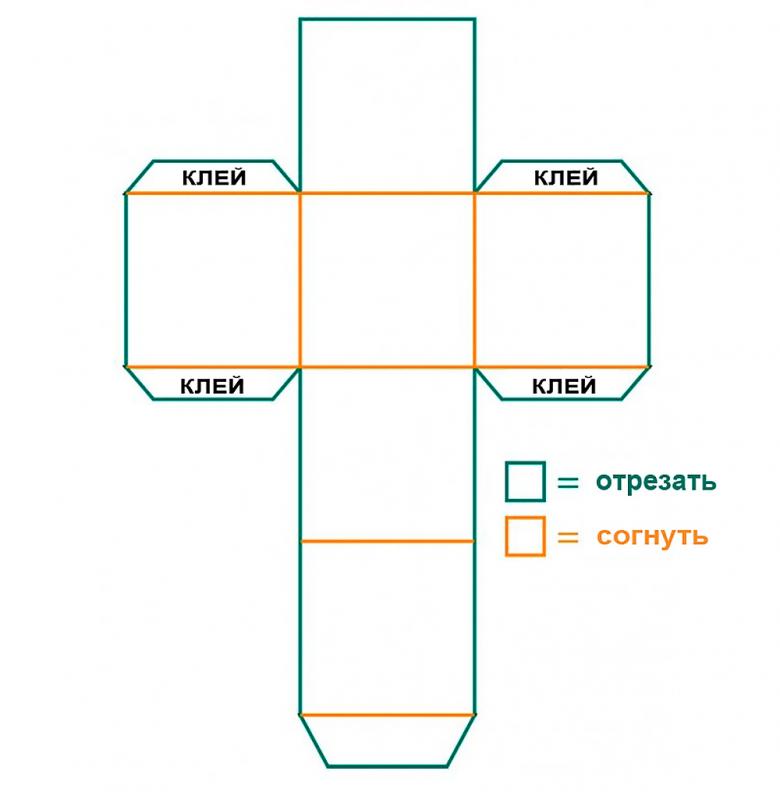
Чтобы проблем не возникало, следует просто учитывать пропорции, и правильно загибать линии. В итоге работы должна получиться коробочка. Если вы испытываете трудности или модель не получается, возьмите готовую коробку (например из-под чая) и просто обклейте ее грани белой бумагой. Это придаст конструкции презентабельный вид и позволит быстро и ровно создать параллелепипед без особых усилий.
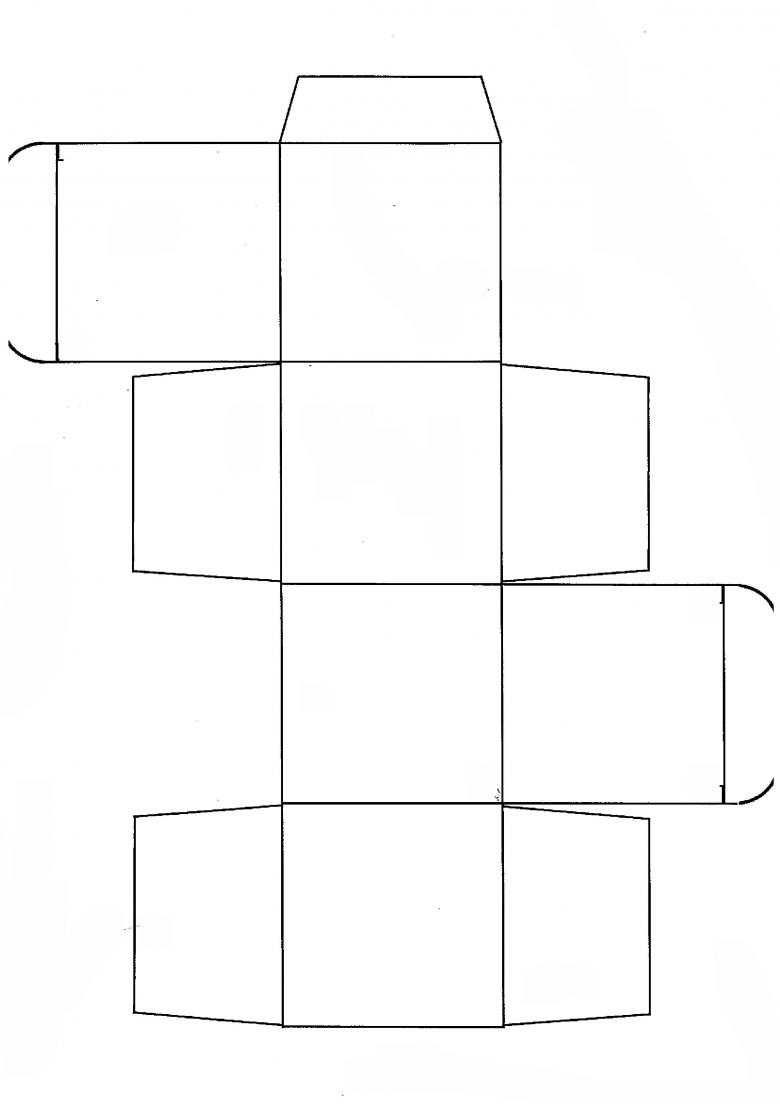
Техника работы со склеиванием модели довольно проста и при наличии практики создаст у ребенка базовое восприятие пространственного мышления. Если модель не получилась с первого раза, проанализируйте ошибку и посмотрите, где неправильно согнута линия или где нужно что-то переделать. Мы уверенны, следующая модель обязательно получиться.
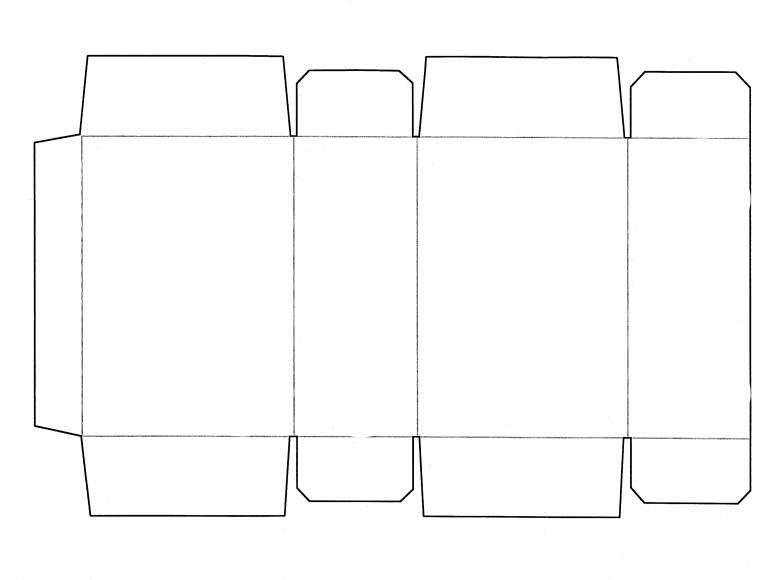
Несколько базовых шаблонов позволит вам быстро и без лишних заморочек создать множество интересных подделок на тему объемного прямоугольника, а главное, позволит занять детей интересным и познавательным делом! Особенно хорошо идея понравиться деткам дошкольного и школьного возраста.
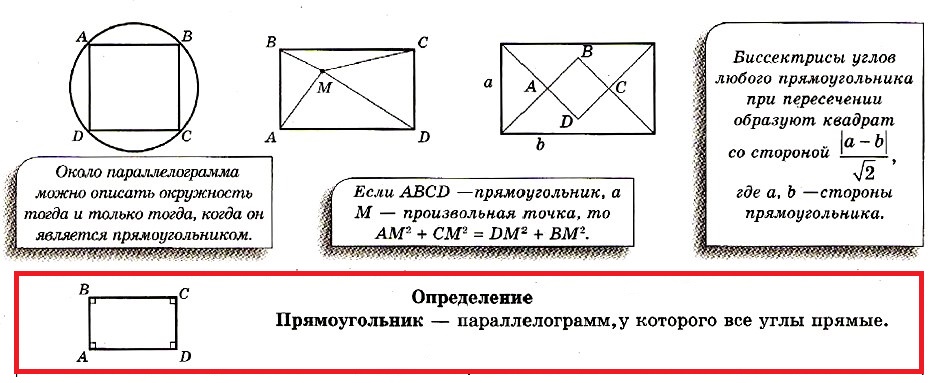
Прямоугольник — параллелограмм, у которого все углы прямые.
Свойства и признаки прямоугольника
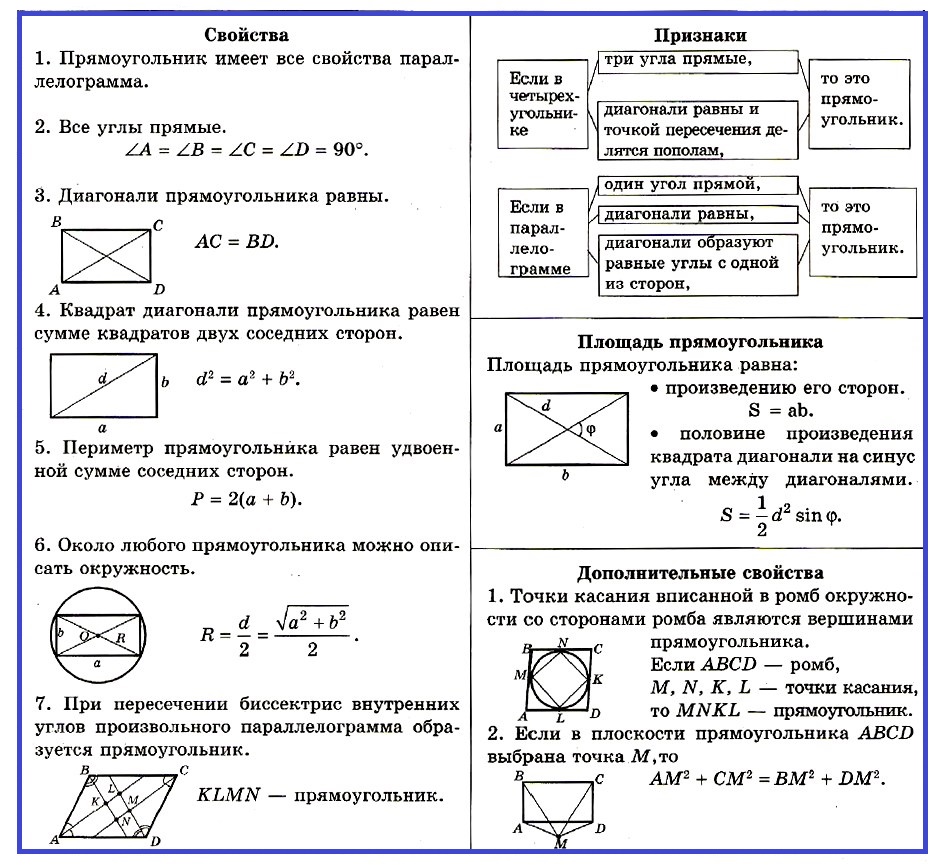
Свойства прямоугольника:
1. Прямоугoльник имеет все свойства параллелограмма.
2. Все углы прямые.
3. Диагонали прямоугольника равны.
4. Квадрат диагонали прямоугольника равен сумме квадратов двух соседних сторон.
5. Периметр прямоугольника равен удвоенной сумме соседних сторон.
6. Около любого прямоугольника можно описать окружность.
7. При пересечении биссектрис внутренних углов произвольного параллелограмма образуется прямоугoльник.
Признаки прямоугольников:
Если в четырехугольнике три угла прямые.
Если в четырехугольнике диагонали равны и точкой пересечения делятся пополам.
Если в параллелограмме один угол прямой, диагонали равны.
Если в параллелограмме диагонали образуют равные углы с одной из сторон.

Если вам сделали сюрприз в подарочной прямоугольной коробке, знайте — это параллелепипед. Кирпич, кстати, тоже яркий пример многогранника с шестью гранями. В этой статье узнаем больше про эту фигуру и дадим примеры разверток для прямоугольного параллелепипеда.
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллелепипеда
Параллелепипед — это многогранник, у которого шесть граней.
У параллелепипеда каждая грань представляют собой параллелограмм, противоположные грани которого равны.

Прямоугольный параллелепипед — это многогранник с шестью гранями, каждая из которых является прямоугольником.
Свойства прямоугольного параллелепипеда
- противоположные грани равны между собой;
- боковые ребра перпендикулярны основаниям, то есть являются высотами.
Диагональ прямоугольного параллелепипеда — это отрезок, который соединяет две противоположные вершины. Все диагонали равны, пересекаются в одной точке и делятся ею пополам.

Схема создания прямоугольного параллелепипеда
Для сборки параллелепипеда нужно распечатать развертку на обычном листе формата А4. Для печати можно использовать белую или цветную бумагу.

Как сделать развертку прямоугольного параллелепипеда:
Развертка прямоугольного параллелепипеда с размерами
Геометрические размеры параллелепипеда №1:
- Длина = 120 мм
- Ширина = 90 мм
- Высота = 40 мм
Прямоугольный параллелепипед с такими размерами выглядит так:

Геометрические размеры параллелепипеда №2:
- Длина = 90 мм
- Ширина = 65 мм
- Высота = 50 мм
Прямоугольный параллелепипед с такими размерами выглядит так:

Геометрические размеры параллелепипеда №3:
- Длина = 60 мм
- Ширина = 40 мм
- Высота = 65 мм
Прямоугольный параллелепипед с такими размерами выглядит так:

Так выглядит соотношение размеров параллелепипедов для представленных разверток:

Развертка может пригодиться, если нужно сделать прямоугольный параллелепипед из бумаги или картона на уроке математики в 5 классе. Кроме школьных уроков эти знания пригодятся работникам производств. Например, на заводе по производству упаковки.
Также развертка помогает решать некоторые задачи. Например, находить кратчайшее расстояние между точками на поверхности геометрического тела.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Читайте также:


