Как сделать производную в маткаде
Продолжаем изучать программы, что помогают работать с математикой. И сегодня я вам немножко начну рассказывать о Mathcad, и более подробно остановимся на решении производных с помощью этой программы .
И так, посмотрев видеоурок, что подан ниже, вы узнаете:
- Как писать в Mathcad;
- Где брать математические функции в этой программе;
- Какие там есть свои нюансы;
- Как с её помощью решать производные сложных функций;
- И даже, как можно находить производные высших порядков.
Вы можете бесплатно скачать Mathcad на 30 дней и видеоурок по этой ссылке: скачать Mathcad .
Ознакомиться с правилами решения таких упражнений вы можете по пошаговым видеоурокам на конкретных примерах, если вы их ещё не смотрели, то обязательно подпишитесь на мою рассылку здесь!
P.S. Вы посмотрели видео и у вас возникли вопросы, то задавайте их в комментариях!

Найти область определения функции
Нужно найти область определения функции y(x)=x+2atan(x) Пожалуйста, кто-нибудь, помогите. Не.

Найти производную функции
рабочей среды нету, прошу у Вас помощи y=2arcsin\frac>-\sqrt^>

Найти производную функции
Найдите производную функции f(x) тремя способами: - по определению; - аналитически, используя.
1) Если Вы работаете с функцией и собираетесь для неё что-то находить или исследовать, то прежде всего эту функцию нужно ввести. Это делается так:
- курсор (красный крестик) устанавливаем в любое место рабочей области(белая область);
- создаём блок с формулой, вводим y(x) Shift+: \ 1-x^2
Комбинация клавиш Shift+: вводит оператор присваивания :=
Обратный слэш (\) вводит операцию извлечения квадратного корня.
- создаём новую функцию y1(x), которая является производной функции y(x).
Для этого курсор (красный крестик) помещаем в новое место рабочей области и печатаем
y1(x) Shift+: Shift + / x y(x) Ctrl+. Enter
Комбинация клавиш Shift + / вводит оператор дифференцирования (нахождения производной)
Там появятся два местозаполнителя: один внизу, в нём записывается переменная дифференцирования (в данном случае x), а другой - боковой, в нём указывается функция (точнее имя функции, а в круглых скобках - аргумент или аргументы).
Комбинация клавиш Ctrl+. вводит оператор вывода символьного результата.
Должно получиться так:
Cute, огромное спасибо, за такой подробный ответ. Только вот у вас решение выводится верное, а у меня почему-то такое:
Cute, огромное спасибо, за такой подробный ответ. Только вот у вас решение выводится верное, а у меня почему-то такое:
darkspringreen, у Вас тоже всё правильно, просто форма записи результата немного другая. Скорее всего это из-за того, что у меня версия Mathcad отличается от Вашей.
Есть такая формула в курсе алгебры:
Cute, а можно-ли как-то сделать, что-бы выводилось как у Вас? Может в версии программы дело или можно определить форму записи результата как-то? Просто сдаю по учебе тесты онлайн, было-бы удобнее выбрать правильный ответ, боюсь в сложных функциях будет напряжно преобразовывать)
Теперь насчёт задания № 2.
Область определения функции – это множество всех значений переменной , при которых выражение для данной функции существует (определено).
Если функция задана формулой вида , то область определения такой функции задаётся системой трёх условий:
1) числитель дроби должен существовать,
2) знаменатель дроби должен существовать,
3) знаменатель дроби не должен равняться нулю.
Для данной функции область определения задаётся системой условий:
Почему-то здесь не получается записать систему условий в редакторе формул, поэтому ниже будет картинка с системой.

Производной функции в точке называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю т.е.
2. Средства дифференцирования в MathCad
Оператор производной предназначен для нахождения значения производной функции в заданной точке.
Вызвать оператор производной можно следующими способами:
Используя ПИ производных и интегралов
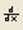
для нахождения производной 1-го порядка
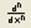
для нахождения производной n-го порядка
Для нахождения производной нужно:
1. 1. Определить точку (или диапазон), в которой будет найдена производная;
2. 2. Вызвать оператор нахождения производной:
v v появится шаблон нахождения производной 1-го порядка

v v шаблон нахождения производной n-го порядка

3. 3. Заполнить шаблон данными:
2.1 Примеры нахождения производных
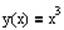
1. Найти производную функции в точке x=2.


2. Найти производную той же самой функции в точках x, на заданном интервале.

3.Найти вторую производную той же функции в точке x=3.5
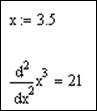
3. Нахождение производной в общем виде
Для вывода на экран формулы нахождения производной необходимо:
v v на ПИ выбрать шаблон неопределенного интеграла производной;
v v заполнить его;
v v набрать на клавиатуре Ctrl+.(точка);
v v нажать ввод.
4. Физический смысл производной
Пусть s=s(t) представляет закон прямолинейного движения материальной точки. Это уравнение выражает путь s, пройденный точкой, как функцию времени t. Обозначим через ∆s путь, пройденный за промежуток времени ∆tот момента t до t+∆t, то есть ∆s=s(t+∆t)-s(t).

Отношение называется средней скоростью точки за время от t до t+∆t.

Мгновенной скоростью точки в данный момент времени t называется предел средней скорости за промежуток от t до t+∆t, когда :
или
Ускорение точки в данный момент вычисляется по следующей формуле:

4.1 Пример применения физического смысла производной

Точка движется по закону . Определить ее мгновенную скорость в момент времени t=5 с.

5. Геометрический смысл производной

Угловой коэффициент касательной к графику функции f(x) в точке a равен первой производной функции в данной точке: , где
β - угол наклона касательной к оси Ох.
Уравнение касательной имеет вид:

- угловой коэффициент касательной к графику функции, в точке x=a
5.1 Пример нахождения уравнения касательной функции в некоторой точке

Найти уравнение касательной к функции , в точке x0 = 2 и ее наклон к оси Ох.

6. Приложения производной
6.1. Экстремумы функции
Правило1 (признак нахождения экстремумов, основанный на исследовании знака первой производной):

Пусть , то если при переходе через точку x0 функция f(x) меняет знак с + на – (с – на +), то x0 – точка локального максимума (минимума).
Правило 2 (признак нахождения экстремумов, основанный на исследовании знака второй производной):
Пусть и , тогда если , то x0 – точка локального максимума (минимума).
Пример нахождения экстремумов функции.

6.2. Разложение функции в ряд Тейлора.
Для приближенного определения значения функции f(x) разложим данную функцию в Ряд Тейлора в окрестности точки x=a.
Применение MathCAD для дифференцирования функций может не только сэкономить время и силы, но и избежать возможных ошибок, неизбежно возникающих при сложных ручных расчетах. Система MathCAD позволяет производить дифференцирование функций как в символьном виде, так и численно.
Символьное дифференцирование можно осуществить тремя способами:
1. Вставить шаблон из панели Calculus, заполнить его и применить команду из меню
Symbolics/Simplify или Symbolics/Evaluate/Symbolically
2. Вставить шаблон из панели Calculus, заполнить его и применить команду символьного вывода или ключевое слово simplify c панели Symbolics (кардинальская шапка);
3. Набрать выражение для функции, выделить переменную, по которой необходимо провести операцию дифференцирования и дать команду из меню
В вышеприведенном примере показано и численное дифференцирование функции в точке x=2, при этом символьная производная запоминается в функции D(x), затем происходит обращение к этой функции и дается команда численного вычисления (знак “=”). Для численного дифференцирования MathCAD применяет довольно сложный алгоритм Риддера, вычисляющий производную с колоссальной точностью до 7-8 знака после запятой. Существенно, что погрешность дифференцирования не зависит от констант TOL и CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом.
Возможности MathCAD позволяют продифференцировать любую непрерывную функцию, но иногда возникает необходимость находить производную от функции вблизи точки разрыва. В математике для дифференцирования функции вблизи точки разрыва используют операцию односторонней производной. В MathCAD нет встроенных операторов для вычисления односторонних производных, но вычислить их все-таки можно. Для этого следует скомбинировать оператор обычной производной с операторами односторонних пределов, как это сделано в нижеприведенном примере
Производные высших порядков. Для вычисления производных высших порядков в MathCAD предусмотрен специальный оператор на панели Calculus. Шаблон этого оператора содержит на два поля ввода больше, чем оператор обычной производной. В эти два поля может быть вписан порядок производной, причем достаточно ввести значение в одном из них, а в другом оно появится автоматически. Производные высших порядков можно вычислять и в символьном виде, и численно, но при численных расчетах вы можете вычислить производную не выше пятого порядка. Это связано с тем, что используемый алгоритм численного дифференцирования очень быстро теряет точность при росте порядка производной. В символьном же виде вычисление производных высших порядков производится так же просто и точно, как и производной первого порядка.
Частные производные. С помощью обоих процессоров MathCAD можно вычислять производные функций любого количества аргументов. В этом случае, как известно, производные по разным аргументам называются частными. Чтобы вычислить частную производную, необходимо, как обычно, ввести оператор производной с панели Calculus и в соответствующем местозаполнителе напечатать имя переменной, по которой должно быть осуществлено дифференцирование. Для того, чтобы изменить вид оператора дифференцирования на представление частной производной, необходимо выбрать из контекстного меню для области оператора дифференцирования пункт View Derivative As (Изображать производную как), в появившемся подменю выбрать пункт Partial Derivative (Частная производная).
Частные производные высших порядков рассчитываются точно так же, как и обычные производные высших порядков.
Читайте также:


