Как сделать призму в изометрии

Обновлено: 08.01.2025

Home Просвещение Графическое отображение Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Способы построения изометрической проекции плоских фигур, геометрических тел и деталей

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

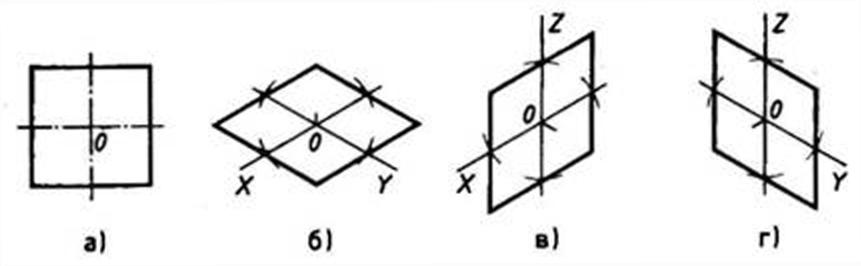
Рис. 109. Прямоугольная и изометрические проекции квадрата

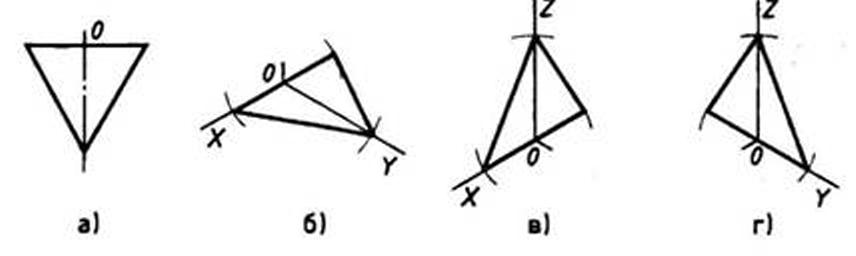
Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

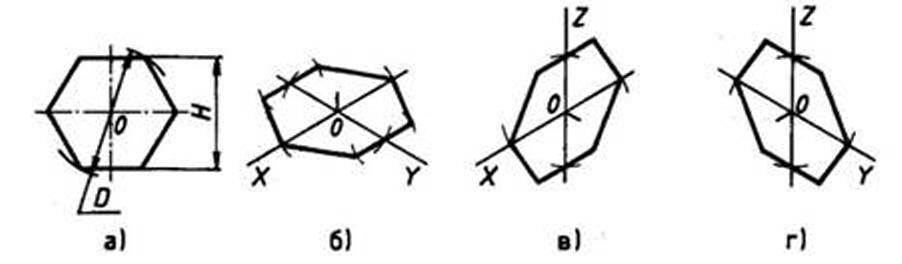
Рис. 111. Прямоугольная и изометрические проекции шестиугольника

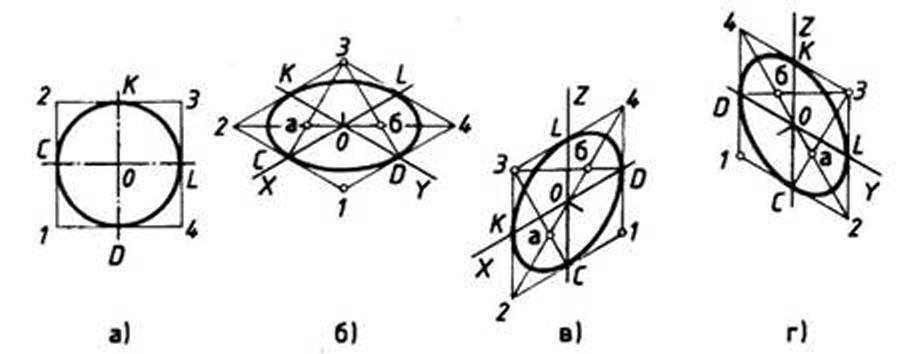
Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

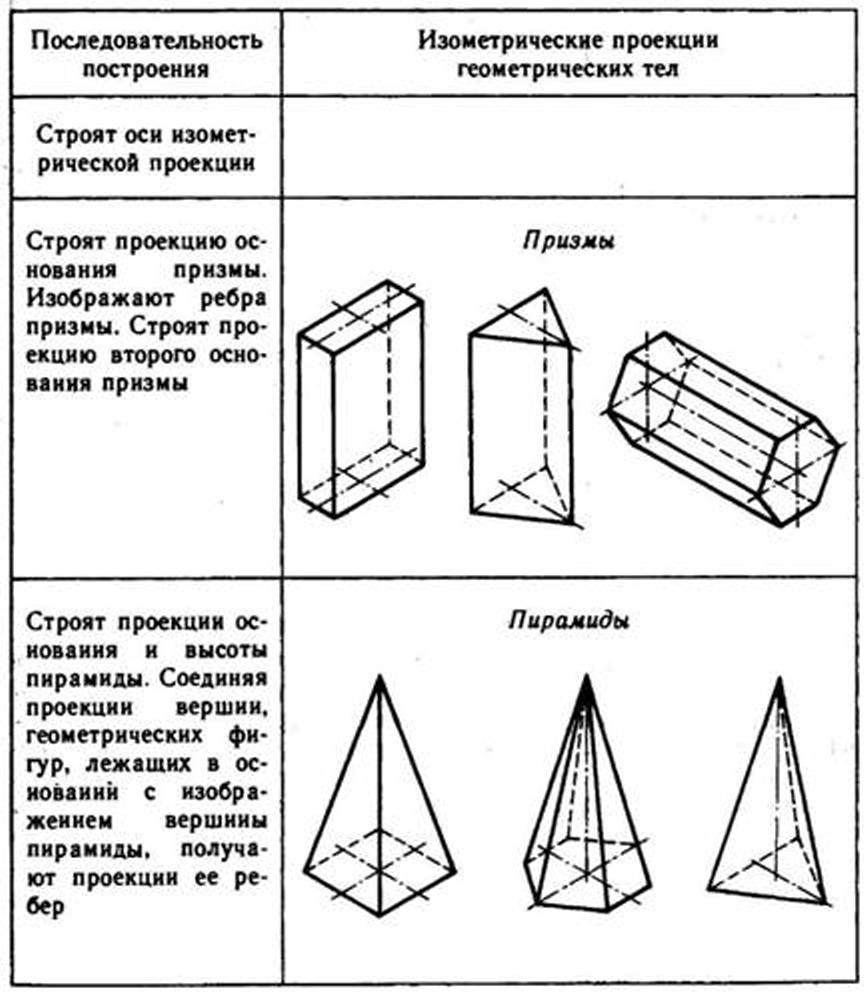
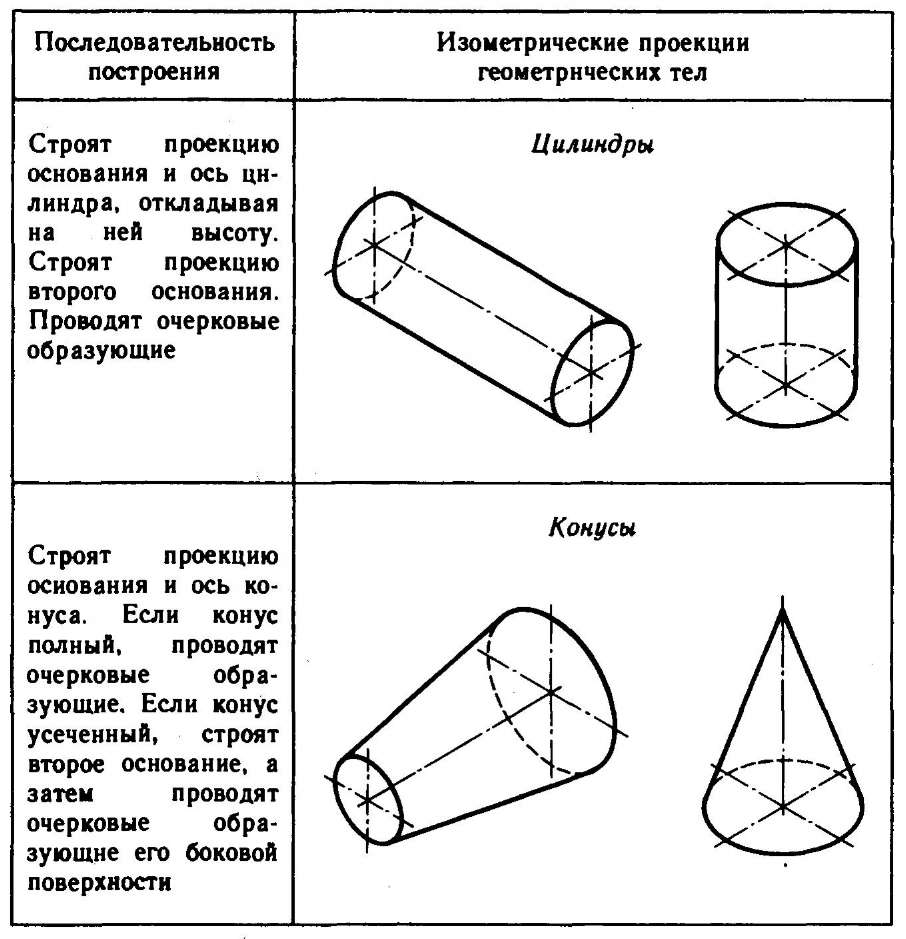
Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

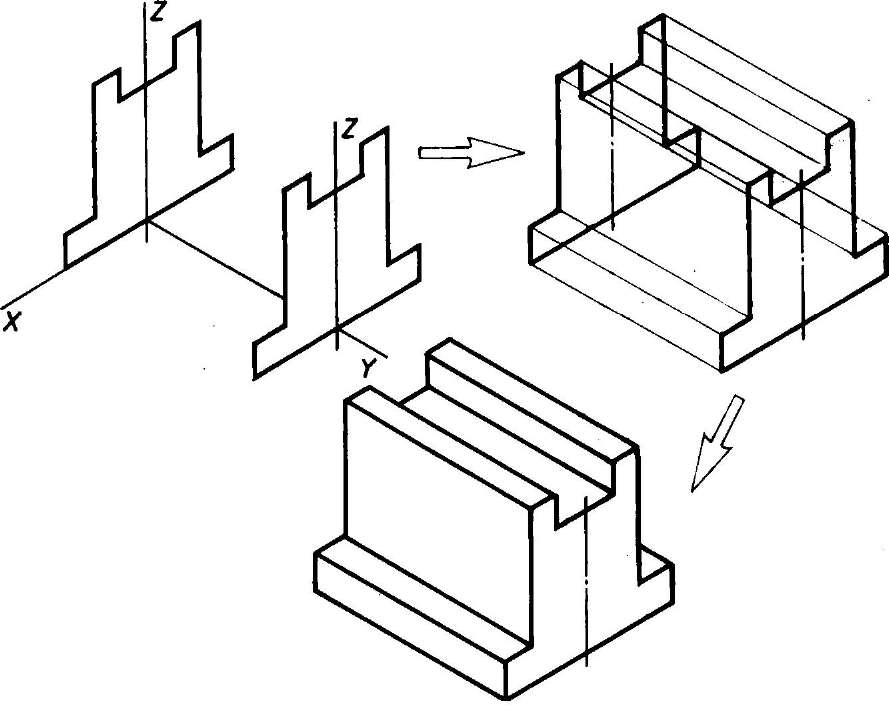
Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис. 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

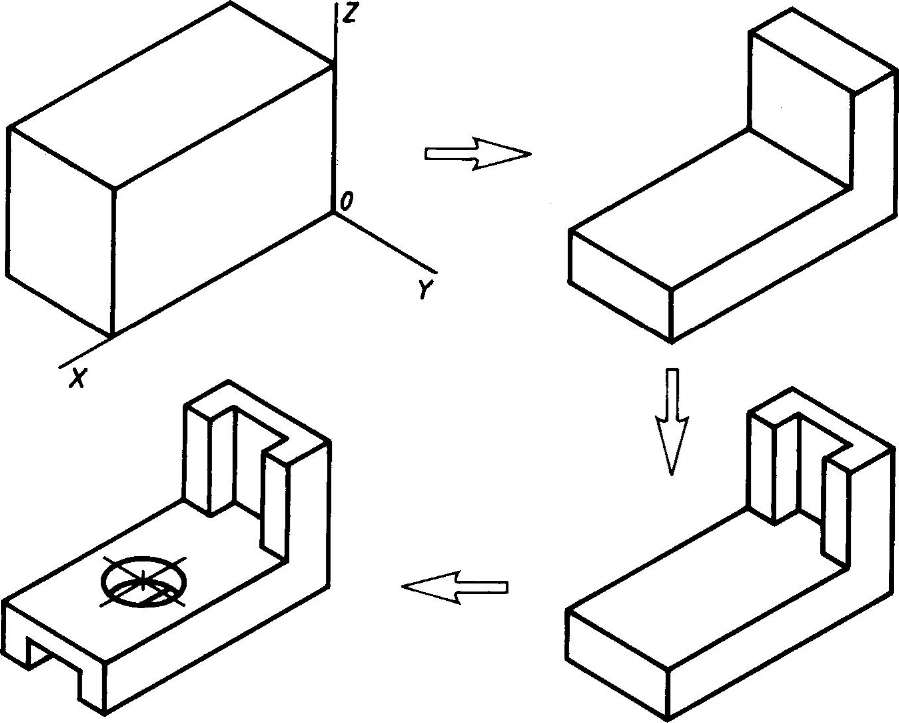
Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

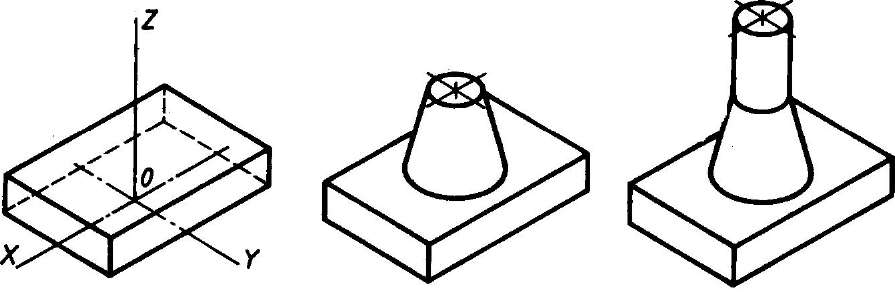
Рис. 115 Построение изометрической проекции детали на основе последовательного приращения объемов

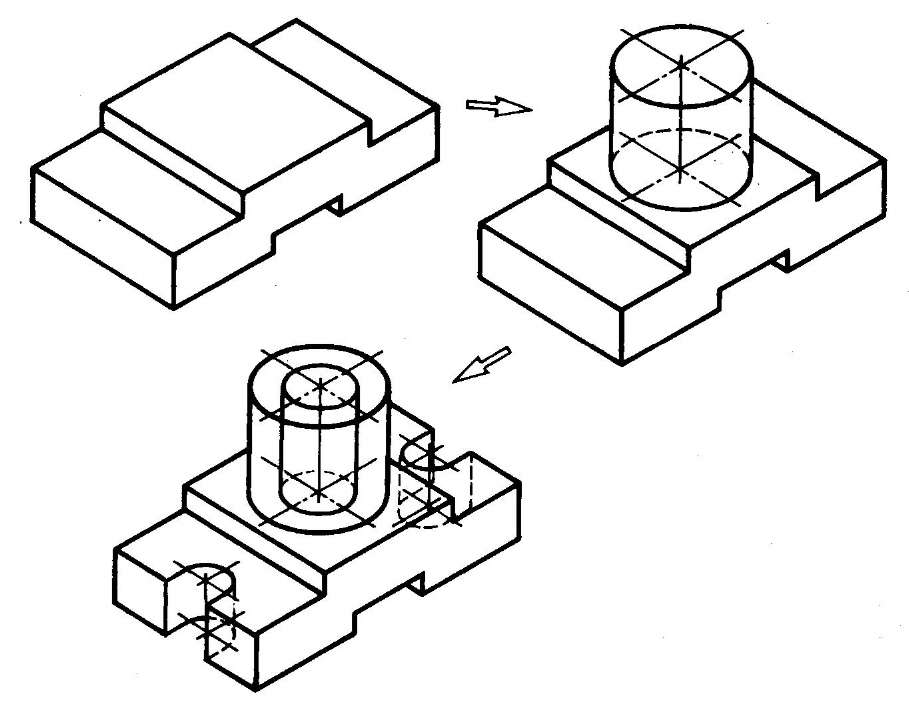
Рис. 116. Использование комбинированного способа построения изометрической проекции детали

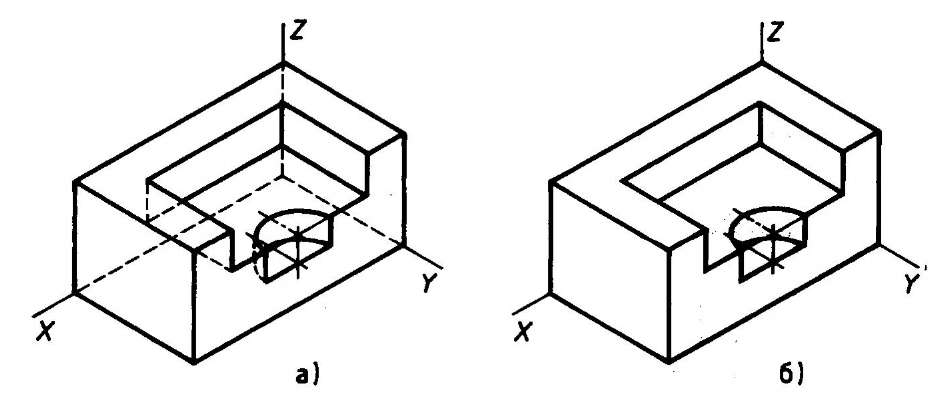
Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;
б — без изображения невидимых частей

Черчение ©2010 Копирование или перепечатка любых материалов сайта возможны только при согласии администрации и активной ссылки на источник

ЦЕЛЬ ЗАДАНИЯ. Научиться изображать шести­гранную призму в различных положениях.

ПОСТАНОВКА ЗАДАНИЯ. Изучите различные способы построения правильного шестиугольника, сделайте рисунки шестиугольников, проверьте правильность их построения. На основе шестиугольни­ков постройте шестигранные призмы.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите шестигранную призму на рис. 3.52 и ее ортогональные проекции на рис. 3.53. В основа­нии шестигранной призмы (шестигранника) лежат правильные шестиугольники, боковые грани — оди­наковые прямоугольники. Для того, чтобы правиль­но изобразить шестигранник в перспективе, необ­ходимо сначала научиться грамотно изображать в перспективе его основание (рис. 3.54). В шестиугольнике на рис. 3.55 вершины обозначены цифра­ми от одного до шести.

Если соединить точки 1 и 3, 4 и 6 вертикальными прямыми, можно заметить, что эти прямые вместе с точкой центра окружности де­лят диаметр 5— 2 на четыре равных отрезка (эти от­резки обозначены дугами). Противоположные сто­роны шестиугольника параллельны друг другу и прямой, проходящей через его центр и соединяю­щей две вершины (например, стороны 6— 1 и 4— 3 параллельны прямой 5— 2). Эти наблюдения помо­гут вам построить шестиугольник в перспективе, а также проверить правильность этого построения.
Построить правильный шестиугольник по представ­лению можно двумя способами: на основе описан­ной окружности и на основе квадрата.
На основе описанной окружности. Рассмотрите рис. 3.56. Все вершины правильного шестиугольни­ка принадлежат описанной окружности, радиус ко­торой равен стороне шестиугольника.

Горизонтальный шестиугольник

Изобразите го­ризонтальный эллипс произвольного раскрытия, т.е. описанную окружность в перспективе. Теперь необ­ходимо найти на ней шесть точек, являющихся вер­шинами шестиугольника. Проведите любой диа­метр данной окружности через ее центр (рис. 3.57).
Крайние точки диаметра — 5 и 2, лежащие на эллип­се, являются вершинами шестиугольника. Для на­хождения остальных вершин необходимо разделить этот диаметр на четыре одинаковых отрезка. Диа­метр уже разделен точкой центра окружности на два радиуса, остается разделить каждый радиус попо­лам. На перспективном рисунке все четыре отрезка равномерно сокращаются при удалении от зрителя (рис. 3.58). Теперь проведите через середины ради­усов — точки А и В — прямые, перпендикулярные пря­мой 5— 2. Найти их направление можно при помощи касательных к эллипсу в точках 5 и 2 (рис. 3.59). Эти касательные будут перпендикулярны диаметру 5— 2, а прямые, проведенные через точки А и В парал­лельно этим касательным, будут также перпендику­лярны прямой 5— 2. Обозначьте точки, полученные на пересечении этих прямых с эллипсом, как 1, 3, 4, 6 (рис. 3.60). Соедините все шесть вершин прямы­ми линиями (рис. 3.61).

Проверьте правильность вашего построения разными способами. Если построение верно, то ли­нии, соединяющие противоположные вершины шестиугольника, пересекаются в центре окружности (рис. 3.62), а противоположные стороны шести­угольника параллельны соответствующим диамет­рам (рис. 3.63). Еще один способ проверки показан на рис. 3.64.

Вертикальный шестиугольник

В таком шести­угольнике прямые, соединяющие точки 1 и 3, 6 и 4, а также касательные к описанной окружности в точ­ках 5 и 2, имеют вертикальное направление и сохра­няют его на перспективном рисунке. Таким обра­зом, проведя две вертикальные касательные к эл­липсу, найдем точки 5 и 2 (точки касания). Соедини­те их прямой линией, а затем разделите полученный диаметр 5— 2 на 4 равных отрезка, учитывая их пер­спективные сокращения (рис. 3.65). Проведите вер­тикальные прямые через точки А и В, а на их пере­сечении с эллипсом найдите точки 7, 3, 6 и 4. Затем последовательно соедините точки 1— 6 прямыми (рис. 3.66). Правильность построения шестиуголь­ника проверьте аналогично предыдущему примеру.

Описанный способ построения шестиугольника позволяет получить эту фигуру на основе окружно­сти, изобразить которую в перспективе проще, чем
квадрат заданных пропорций. Поэтому данный спо­соб построения шестиугольника представляется наиболее точным и универсальным. Способ постро
ения на основе квадрата позволяет легко изобра­зить шестигранник в том случае, когда на рисунке уже есть куб, иными словами, когда пропорции квадрата и направление его сторон определены.
На основе квадрата. Рассмотрите рис. 3.67. Вписанный в квадрат шестиугольник по горизон­тальному направлению 5— 2 равен стороне квадра­та, а по вертикали — меньше ее длины.

Вертикальный шестиугольник

Нарисуйте вер­тикальный квадрат в перспективе. Проведите через пересечение диагоналей прямую, параллельную его горизонтальным сторонам. Разделите полученный отрезок 5— 2 на четыре равные части и проведите через точки А и В вертикальные прямые (рис. 3.68).
Линии, ограничивающие шестиугольник сверху и снизу, не совпадают со сторонами квадрата. Изоб­разите их на некотором расстоянии (1/14 а) от гори­зонтальных сторон квадрата и параллельно им. Со­единив найденные таким образом точки 1 и 3 с точ­кой 2, а точки 6 и 4 — с точкой 5, получим шести­угольник (рис. 3.69).

Гэризонтальный шестиугольник строится в той же последовательности (рис. 3.70 и 3.71).

Этот способ построения уместен только для ше­стиугольников с достаточным раскрытием. В слу­чае, если раскрытие шестиугольника незначитель­но, лучше воспользоваться способом на основе описанной окружности. Для проверки шестиуголь­ника, построенного через квадрат, можно использо­вать уже известные вам методы.

Кроме того существует еще один — описать вок­руг полученного шестиугольника окружность (на ва­шем рисунке — эллипс). Все вершины шестиуголь­ника должны принадлежать этому эллипсу.

Овладев навыками изображения шестиугольни­ка, вы свободно перейдете к изображению шести­гранной призмы. Внимательно рассмотрите схему
на рис. 3.72, а также схемы построения шестигран­ных призм на основе описанной окружности (рис. 3.73; 3.74 и 3.75) и на основе квадрата (рис. 3.76; 3.77 и 3.78).

Изобразите вертикальные и горизон­тальные шестигранники различными способами. На рисунке вертикального шестигранника длинные стороны боковых граней будут параллельными друг другу вертикальными прямыми, а шестиугольник
основания будет тем больше раскрыт, чем дальше он находится от линии горизонта. На рисунке гори­зонтального шестигранника длинные стороны боко­вых граней будут сходиться в точке схода на гори­зонте, а раскрытие шестиугольника основания бу­дет тем больше, чем дальше от зрителя он находит­ся. Изображая шестигранник, следите также за тем, чтобы параллельные грани обоих оснований сходи­лись в перспективе (рис. 3.79; 3.80).

Построение изображений многоугольников сводится к построению аксонометрических проекций их вершин, которые соединяют между собой прямыми линиями.

Пример построения прямой пятигранной призмы в изометрии.

В прямоугольной изометрической проекции оси образуют между собой углы в 120°,
ось Z направлена вертикально, коэффициент искажения по осям принимают равным 1

Аксонометрия или аксонометрическая проекция – это параллельная проекция на одну плоскость любого геометрического элемента и осей координат, к которым относится этот геометрический элемент. На комплексном чертеже (эпюре) в ортогональных проекциях отображено положение точки, прямой, поверхности относительно плоскостей проекции. Расстояние этих геометрических элементов от плоскостей проекций являются их натуральными координатами.

• Как сделать аксонометрию
• Как построить окружность в аксонометрии
• Как строить аксонометрию

• - карандаш;
• - линейка;
• - циркуль;
• - треугольник.

При проектировании на плоскость аксонометрических проекций П’ натуральной системы координат Oxyz получится аксонометрическая система координат O’x’y’z’, а проекция любой точки – аксонометрической проекцией или аксонометрией A’ (рисунок 1). Если перенести с эпюра горизонтальную проекцию точки A₁ в новую систему, это будет так называемая вторичная проекция и точка будет иметь аксонометрические координаты.

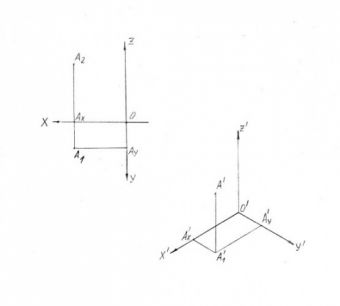
Отношение аксонометрических координат к натуральным называется показателями искажения по осям. Они обозначаются u, v, w, а величина углов между аксонометрическими осями – соответственно α, β и γ.
Существуют различные виды аксонометрии. В машиностроительном черчении чаще применяется прямоугольная аксонометрия. В зависимости от величины показателей искажения u, v, w прямоугольная аксонометрия делится на виды:

- изометрия – показатели искажения по всем трем осям равны между собой u=v=w.
- диметрия – показатели искажения равны по двум осям u=w≠v.

Обычно показатели искажения u, v, w имеют дробные значения, но для упрощения построений используются их приведенные значения. Например, в изометрии приведенные координаты равны натуральным.

Пример. Построить прямоугольную изометрическую проекцию призмы (рисунок 2).
Комплексный чертеж призмы задан в системе осей xyz, начало координат – точка О.

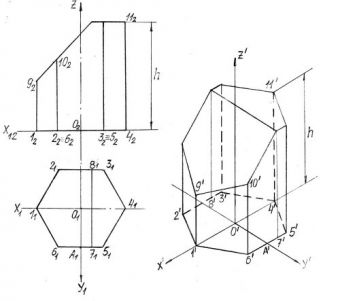
В аксонометрических осях постройте вторичную проекцию призмы. Пусть начало координат точка O’ и ось z’ пройдет через основную ось призмы z. Все размеры с комплексного чертежа перенесите на оси x’O’y’ без изменений, т.к. коэффициенты искажения по осям равны 1.
От точки O’ отложите отрезок О₁1₁ и О₁4₁ по оси x’. Отметьте точки 1’ и O’, а по оси y’ отложите отрезок О₁А₁. Получите точки O’, A’.

На эпюре отрезок 6₁5₁ параллелен оси x₁, значит, и отрезок 6’5’ проведите параллельно оси x’. Отложите на нем расстояние А₁6₁ и А₁5₁. Отметьте полученные точки 6’, 5’ и аналогично постройте симметричные им точки 2’, 3’.

Определите положение точек 7’ и 8’, отложив размеры 7₁А₁. Таким образом, в аксонометрической проекции построена вторичная проекция основания призмы – 1’,2’,…8’. Из каждой точки проведите прямые, параллельные оси Z’. На этих прямых отложите высоту каждой точки с фронтальной проекции призмы на эпюре.
От точки 1’ отложите отрезок 1₂9₂, а от точек 2’ и 6’ – отрезок 2₂10₂. От остальных точек 3’, 4’ и т.д. отложите отмеченную высоту h. Соединив все построенные точки, получите аксонометрию данной призмы.

Читайте также:

  
• Как сделать пиво из кваса
  
• Как сделать много денег в payday 2
  
• Как сделать из геркулеса гранолу
  
• Как сделать массаж при вальгусном плоскостопии
  
• Как сделать свою идеологию в rimworld