Как сделать правильный 7 угольник
Python turtle рисует правильные многоугольники и многоугольники
Python turtle рисует правильные многоугольники и многоугольники
Правильный многоугольник
Сумма внутренних углов правильного n-стороннего многоугольника:x = (n - 2) * 180° / n

Правильный многоугольник

Самый простой многоугольник - этоПентаграмма
Рассчитать внутренний угол

Вот мой метод. Если у учащихся есть свои методы, поделитесь ими в комментариях.
Как показано на рисунке, в центре пятиконечной звезды находится правильный пятиугольник, а внутренний угол правильного пятиугольника, по расчетам, составляет 108 °.
Маленький треугольник на рисунке - это равнобедренный треугольник, поэтому острый внутренний угол пятиконечной звезды равен (180-2 * 72) = 36 °.
Правильный шестиугольник, правильный семиугольник . то же самое.
Таким образом получается формула для положительного острого внутреннего угла n: z = 2x-180, где: x = (n-2) * 180 / n
Упрощенно: z = (1-4 / n) * 180 °
Код чертежа

Сделайте угловой многоугольник
Если это правильный n-угол, положитеДве смежные вершины соединеныВверх, то по мере увеличения n изображение будет приближаться⚪

Фигура с 19 углами выглядит следующим образом:
Итак, мы должны позволитьДве самые дальние вершиныПодключить
Обратите внимание на угловой многоугольник



Могу желать смело угадывать закон:
n - нечетное число, острый угол при вершине правильного n-стороннего многоугольника с четкими краями: w = (n-1) / 2 * x- (n-3) / 2 * 180
и x = (n-2) * 180 / n
Упрощенно: w = 180 / n
Поскольку n - четное число, после рисования и анализа делается вывод, что w = 360 / n
Краткое заключение
Угловой правильный n-угол острый угол при вершине w
w = 180 / n (n - нечетное число)
w = 360 / n (n - четное число)
Единая формула:w = 90/n * (3+(-1) n )

Проблемы с кодом
Код в соответствии сОстрый угол при вершинеЧтобы нарисовать картинку, из заключения рассчитывается острый угол при вершине.
Угловой правильный n-угол острый угол при вершине w
w = 180 / n (n - нечетное число)
w = 360 / n (n - четное число)
Существуют нечетные числа n1 и четные числа n2 такие, что w1 == w2. Такие как 3 и 6, 5 и 10, 7 и 14 .
Эти пары четности получают одинаковые w, поэтому нарисованная графика одинакова.
В воображении обычная десятиугольная форма выглядит так:
на самом деле это:
анализ проблемы
- Глядя только на нечетные числа, невозможно получить одинаковое w для всех нечетных чисел.
- СтавитьчетныйРазделены на две категории:Кратно 4,Не кратно 4。
- Оно не кратно 4. После того, как 360 / n уменьшится на 2, получится нечетное число 180 /. Ему должно быть равно нечетное число w. Следовательно, программа не может быть нарисована (вы можете написать другую программу для рисования).
Гаусс и гептагон
Следующее изображение представляет собой гауссовское изображение надгробия, предоставленное пользователями сети:
Сделайте правильный семиугольник
подводить итоги
Черепаха рисует графику, и когда направление поворачивается на 360 °, она возвращается в исходное направление, которое можно использовать для расчета количества раз рисования цикла.
При рисовании многоугольников многие выводы делаются и наблюдаются невооруженным глазом, которым не хватает строгих доказательств.
Наконец, если учащиеся обнаруживают ошибки в тексте, пожалуйста, исправьте меня.
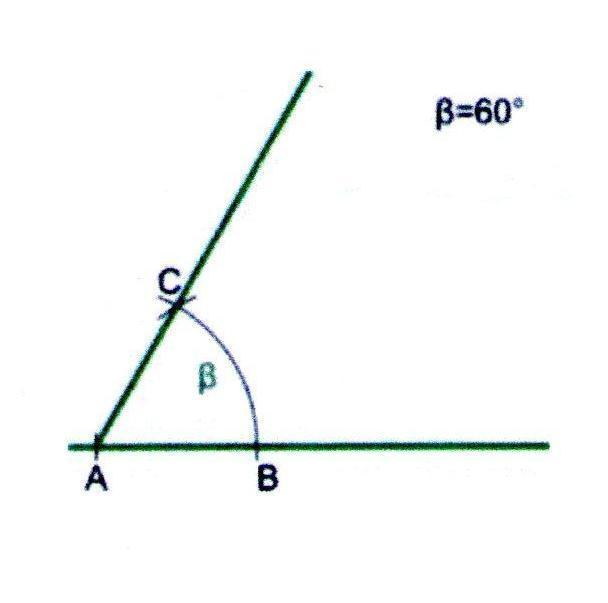
2. Из точки А проведём дугу произвольного радиуса и получим точку В.
3. Из точки В проведём дугу радиуса АВ, чтобы она пересекла ранее начерченную дугу.
4. Проведённая через точку пересечения (С) и точку А прямая будет второй стороной требуемого угла.
Построение угла в 45
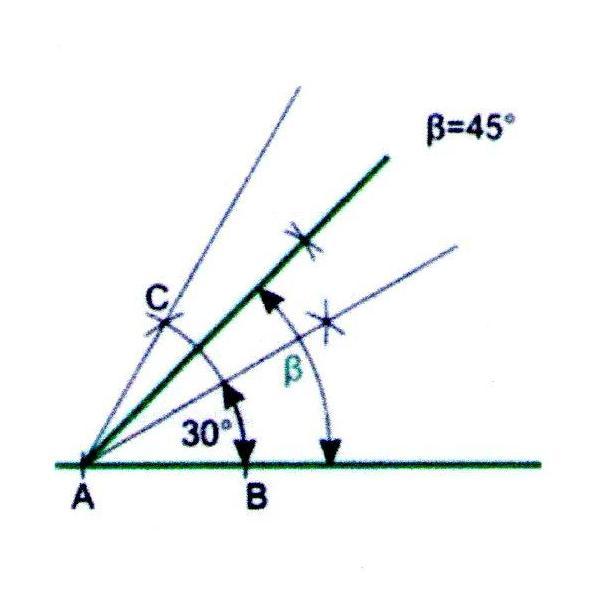
1. Построим угол 60, кака описано выше.
2. Разделим полученный угол пополам.
3. Угол между лучами 60 и 30 разделим пополам. В результате получим угол в 45.
Построение угла в 75
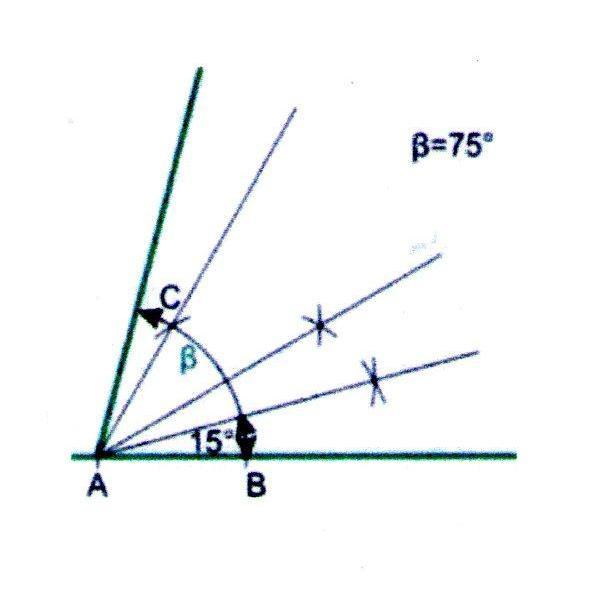
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. В ходе дальнейшего деления надвое получим угол в 15.
3. Отразим угол в 15 через луч 60 и так получим угол в 75.
Построение угла в 90
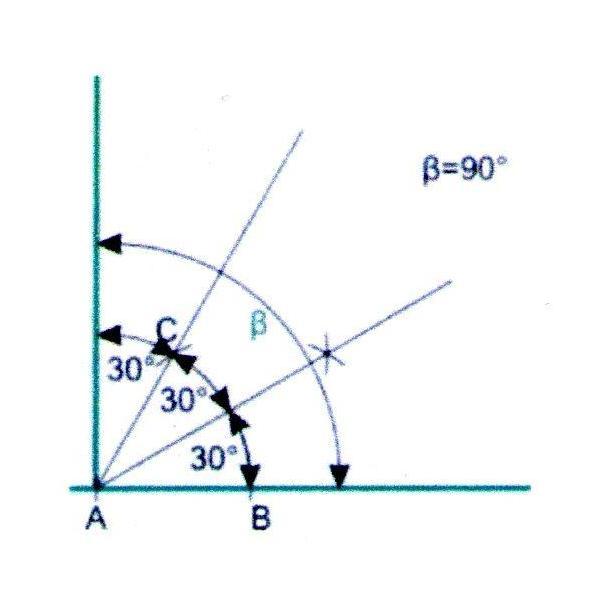
1. Построим угол в 60, как описано выше, и разделим его пополам.
2. Получившийся угол в 30 через луч 60 и так получим угол точно в 90.
Разделение отрезка на равные части.
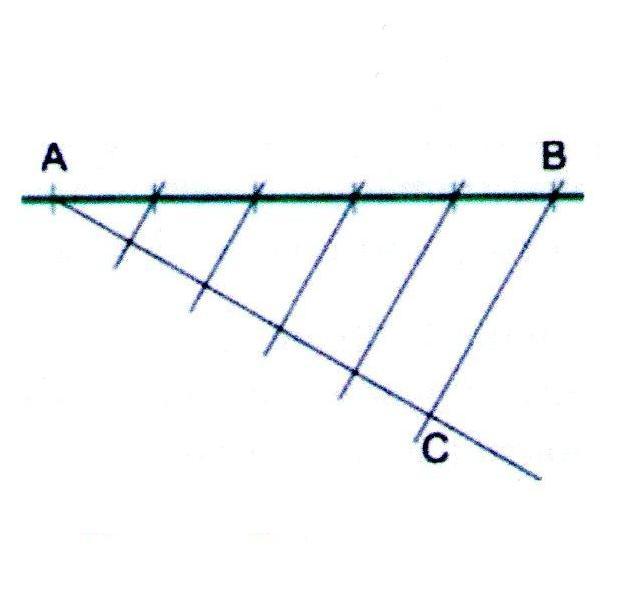
1. Проведём прямую и отметим на ней отрезок АВ.
2. Из точки А проведём вспомогательную прямую и разделим её на столько одинаковых частей, на сколько требуется разделить отрезок АВ. Делить будем при помощи циркуля. Последнюю точку обозначим буквой С.
3. Последнюю точка (С) соединим с концом отрезка АВ. Построим рад параллельных отрезку СВ прямых по всей длине отрезка АВ. Точки пересечения параллельных прямых с отрезком АВ и будут точками раздела отрезка на несколько равных частей.
Построение правильного пятиугольника.
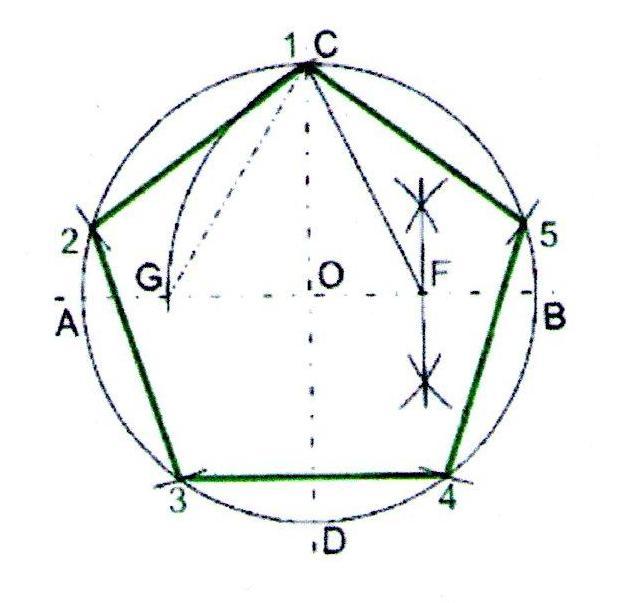
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Разделим пополам расстояние ОВ. Разведём ножки циркуля на расстояние FC . Из точки F проведём дугу через С. Дуга пересечёт горизонтальную линию в точке G .
3. Расстояние CG будет длиной стороны пятиугольника. Из вершины С отложим пять раз расстояние CG .
Построение правильного шестиугольника.
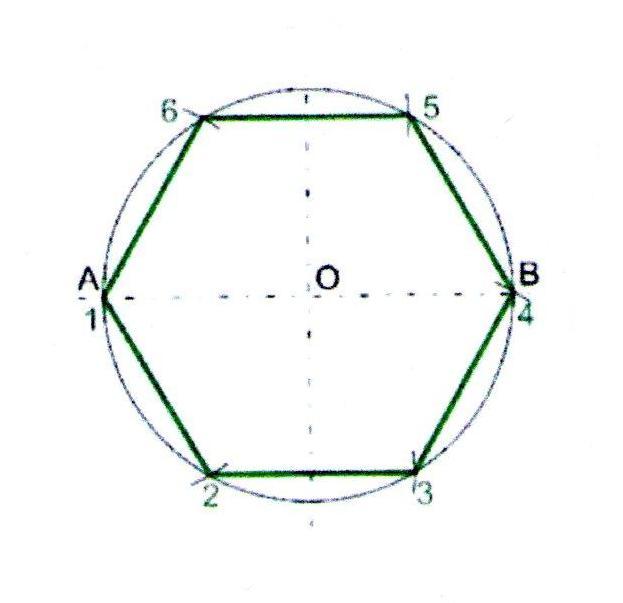
1. Проведём окружность радиусом 50 мм.
2. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
3. Из точки А на линии окружности отложим шесть раз радиус нашей окружности. Соединив прямыми точки пересечения, получим шестиугольник.
Построение правильного семиугольника.
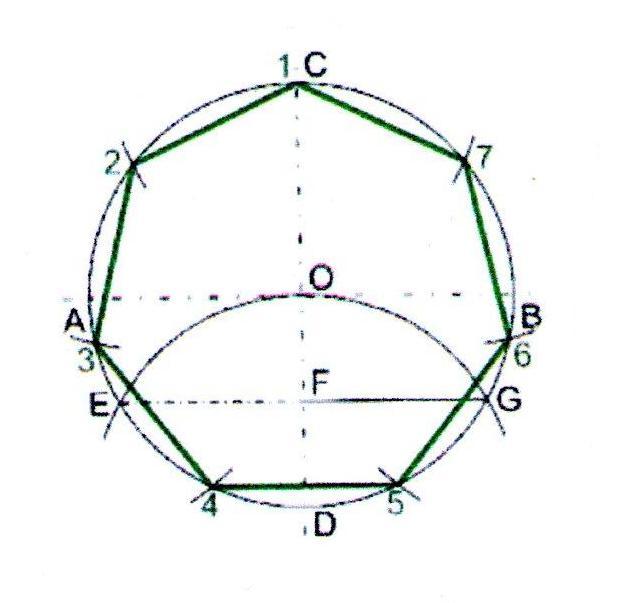
1. Проведём окружность заданного радиуса. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии.
2. Из точки D проведём дугу радиусом равным радиусу окружности.
3. Дуга пересечёт окружность в точках E и G .
4. Длина отрезка EF на хорде EG равна длине стороны семиугольника. Из вершины С семь раз отложим расстояние EF .
Общий метод построения многоугольников.
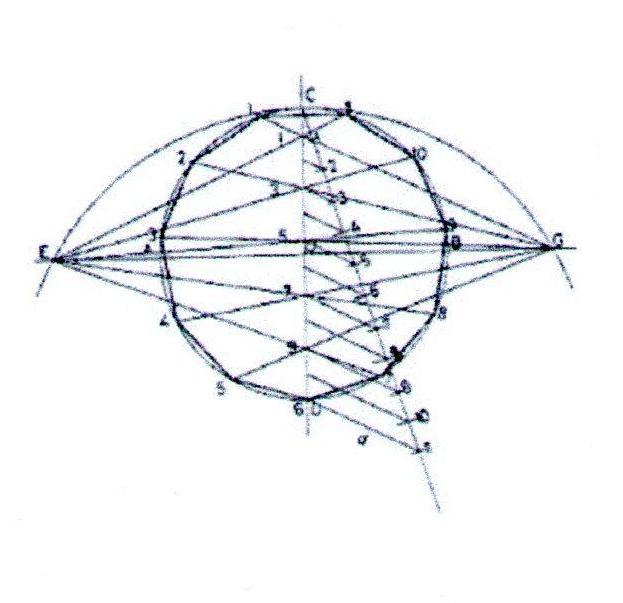
1. Проведём окружность радиусом 50 мм. Через центр окружности проведём взаимно перпендикулярные горизонтальную и вертикальную линии. Продолжим горизонтальную лини. За точки А и В.
2. Из точки D проведём дугу радиусом, равным радиусу окружности так, чтобы дуга пересекла горизонтальную линию.
3. При помощи вспомогательной прямой разделим вертикальную линию на столько равных частей, сколько сторон многоугольника требуется получить. Для примера показано построение одиннадцатиугольника.
4. Из точки Е проведём прямые через нечётные точки раздела вертикальной линии так, чтобы эти прямые пересекли окружность. Такую же операцию проведём из точки G . Полученные лучи пересекают окружность в точках, соединив которые прямыми получаем одиннадцатиугольник.
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.
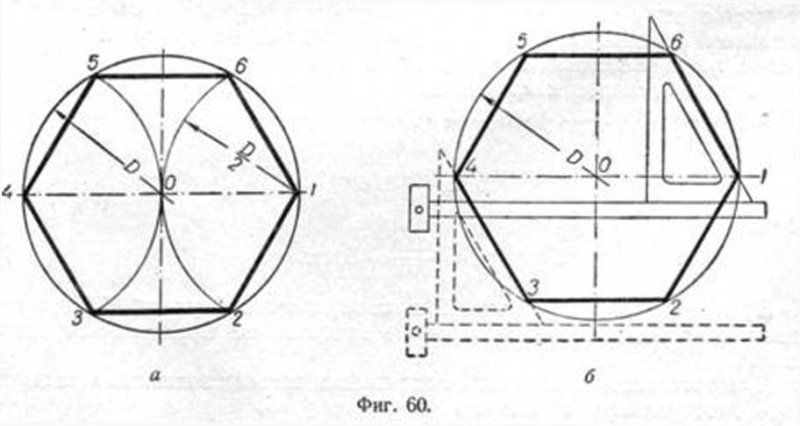
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.
Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
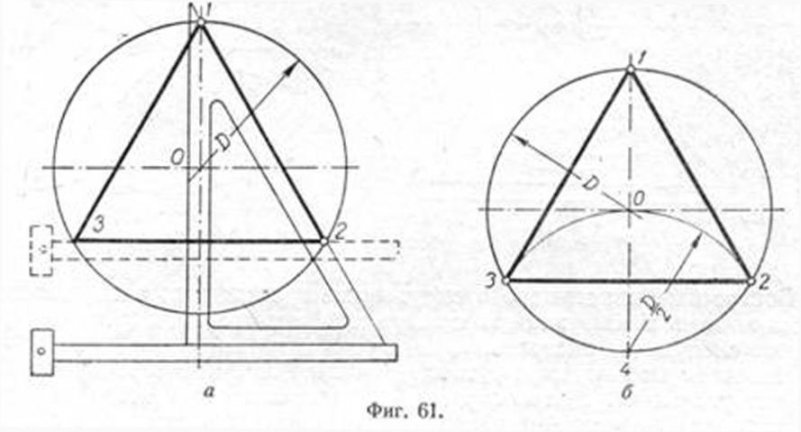
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Это построение можно выполнить при помощи угольника и циркуля.
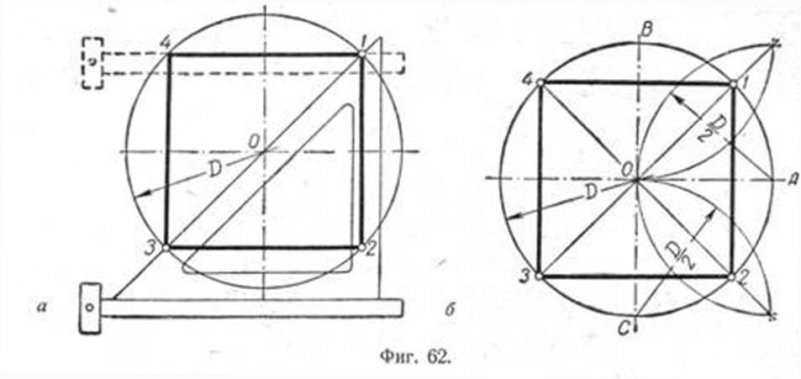
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 —2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
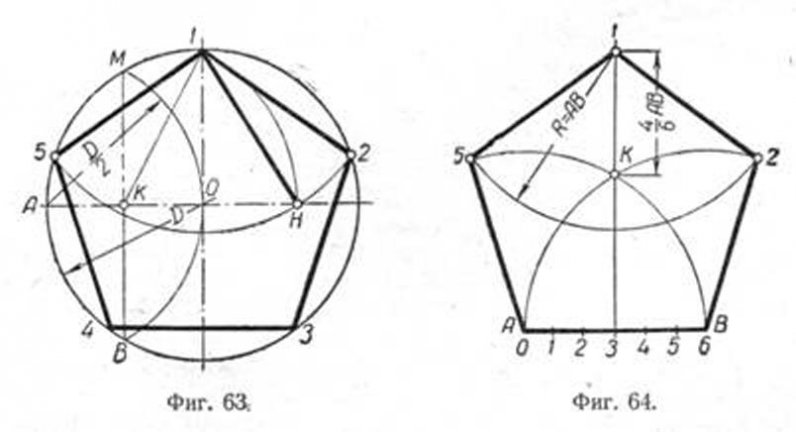
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 —вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
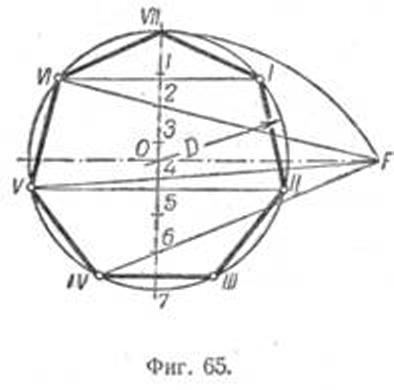
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
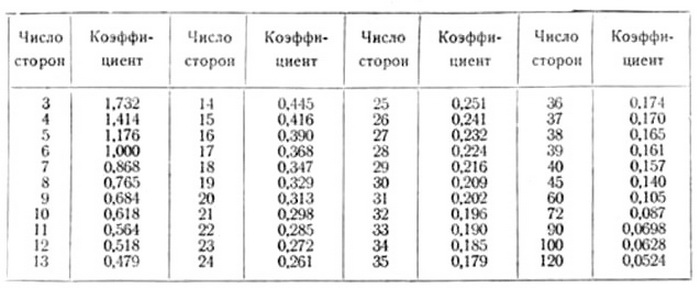
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
Есть отрезок СD. Задача - начертить равнозначный данному отрезок той же величины.
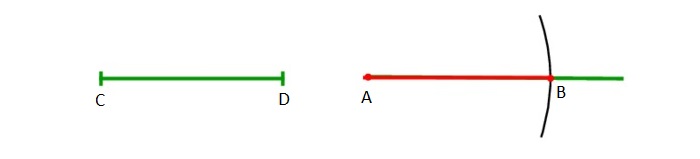
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
Имеется угол ABC.
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка - AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
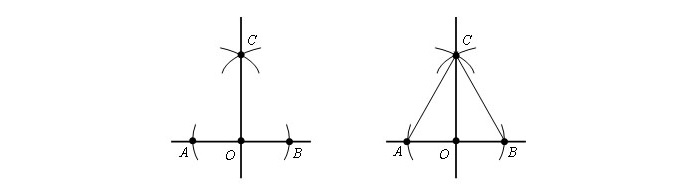
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 - место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
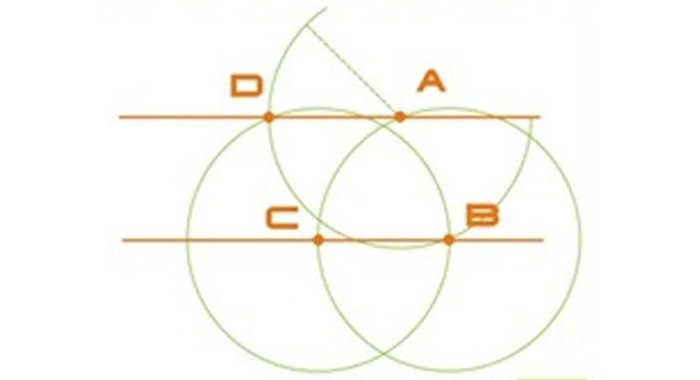
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
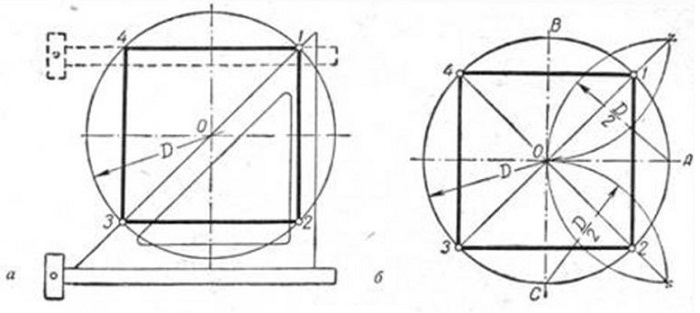
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
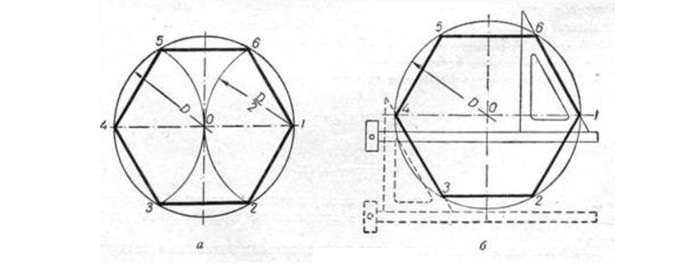
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.

В этом видеофрагменте мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Построение правильных многоугольников"
На этом уроке мы рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. А также изобразим правильный многоугольник графически.
Для начала давайте вспомним определение правильного многоугольника. Итак, правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Для выполнения построений мы используем циркуль и линейку.
Циркуль позволяет:
– построить дугу окружности,
– отложить на прямой отрезок, равный данному.
Линейка позволяет:
– построить прямую линию,
– построить отрезок, соединяющий две точки,
– найти точку пересечения двух прямых.
Ранее мы с вами уже рассматривали построения правильного треугольника и четырехугольника, т.е. квадрата.
Давайте рассмотрим, каким образом можно с помощью циркуля и линейки построить правильный треугольник и правильный четырехугольник, вписанные в окружность.
Задача 1. Вписать в заданную окружность правильный треугольник
Построение. Пусть задана окружность с центром О. Проведем произвольный диаметр BD окружности. Построим прямую l, являющуюся серединным перпендикуляром к радиусу OD. Середину радиуса ОD обозначим точкой К. Отметим точки А и C – пересечения прямой l с окружностью. И построим отрезки BA и BC. Треугольник ABC – правильный.
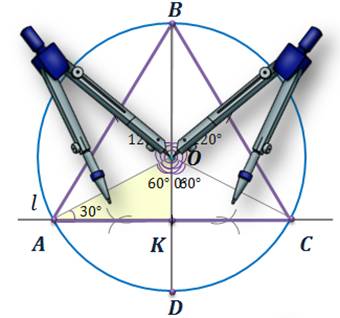
Доказательство.
Значит, – равносторонний – правильный.
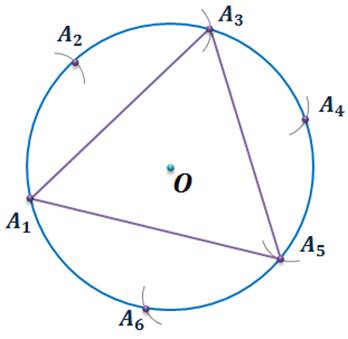
Второй способ построения.
Пусть задана окружность с центром О. Раствором циркуля, равным радиусу, последовательно от одной точки окружности делаем на ней засечки, пока последняя засечка не совпадет с взятой первоначально точкой. Соединив полученные точки через одну, получим правильный треугольник.
Задача 2. Вписать в заданную окружность правильный четырехугольник.
Построение. Пусть задана окружность с центром О. Построим диаметр AC. Затем построим диаметр BD перпендикулярный диаметру AC. Точки А, C и B, D – точки пересечения диаметров с окружностью. И построим отрезки АB, BC, CD и АD. Четырехугольник ABCD – правильный.
Доказательство.
Т.к. , , то – параллелограмм.
Т.к. ,то – прямоугольник.
Значит, – правильный четырехугольник.
Теперь давайте рассмотрим построения правильных n-угольников при n>4. Обычно для построения таких n-угольников используется окружность, описанная около многоугольника.
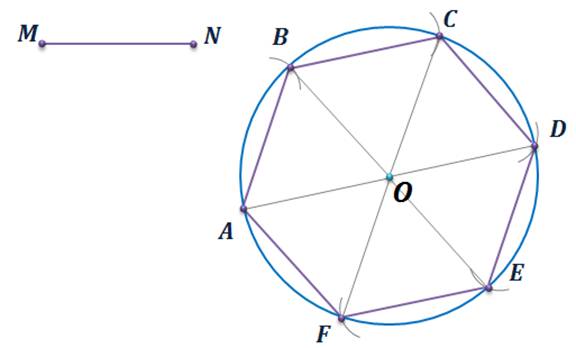
Задача 3. Построить правильный шестиугольник, сторона которого равна данному отрезку.
Построение. Так как в правильном шестиугольнике сторона а равна радиусу, то достаточно последовательно отложить от одной точки окружности 6 радиусов-хорд. Пусть МN – заданный отрезок. Построим окружность с произвольным центром О и радиуса MN. Отметим на этой окружности произвольную точку А. Затем, не меняя раствора циркуля, последовательно от этой точки А будем делать на окружности засечки, пока последняя засечка не совпадет с взятой первоначально точкой А. Отметим точки B, C, D, Е и F. Теперь соединим последовательно построенные точки отрезками. Получим искомый правильный шестиугольник ABCD.
Доказательство.
Равные хорды стягивают равные дуги.
Все углы шестиугольника будут равны, так как опираются на дуги, состоящие из четырех равных меньших дуг.
Для построения правильных многоугольников часто используется следующая задача: дан правильный n-угольник. Построить правильный 2n-угольник.
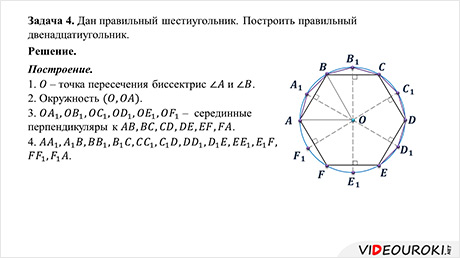
Задача 4. Дан правильный шестиугольник. Построить правильный двенадцатиугольник.
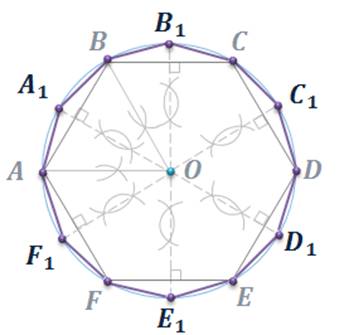
Пусть ABCDEF – данный правильный шестиугольник. Опишем около него окружность.
1. – точка пересечения биссектрис и .
5. – правильный двенадцатиугольник.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырехугольник, т.е. квадрат, и пользуясь задачей 4, можно построить правильный восьмиугольник, затем правильный шестнадцати-угольник и вообще правильный 2 k угольник, где k – любое целое число, большее 2.
Замечание. Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Но важно заметить, что не все правильные многоугольники могут быть построены таким образом.
Подведем итоги урока.
Сегодня мы рассмотрели способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Научились строить правильные треугольник и четырехугольник, вписанные в окружность. А также выполнили задачу на построение правильного многоугольника по заданному отрезку, и задачу на построение правильного 2n-угольника по заданному n-угольнику.
Читайте также:



