Как сделать поверхность в матлабе

Обновлено: 24.01.2025

Графики в Matlab, также как в табличном процессоре, могут быть построены по узловым точкам. Поскольку MATLAB — матричная система, совокупность узловых точек у(х) для построения графика задается векторами X и Y одинакового размера.

Графики MATLAB строит в отдельных окнах, называемых графическими окнами. В главном меню окна есть позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.

В Matlab для построения графиков функций по узловым точкам в декартовой системе координат служит функция plot. Функция plot имеет несколько синтаксических конструкций:
- plot (X, Y) - строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы;
- plot(Y) — строит график у(i), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y), imag(Y)). Во всех других случаях мнимая часть данных игнорируется;
- plot(X,Y,S) — аналогична команде plot(X,Y), но тип линии графика можно задавать с помощью строковой константы S. Значениями константы S могут быть следующие символы:

Если функция задана аналитической моделью, то для построения графика нужно определить вектор значений аргумента для узловых точек, вычислить значения функции при заданных значениях аргумента и сохранить эти значения в виде вектора, а затем применить функцию plot. Приведенный ниже пример иллюстрирует построение графика функций — sin(x) по узловым точкам :

>> x=[0; 0.4; 0.8; 1.2; 1.4;1.8;2.2;2.6;3;3.4;3.8]; Y=sin(x); plot(x,Y)

В этом примере уже определены значения вектора x , вычисляемые значения функции содержатся в векторе Y.

Построение двумерного графика одной функции

Для того, чтобы построить график функции y = f(x) , необходимо сформировать два одномерных массива x и y одинаковой размерности, а затем использовать функцию plot .

Пример 1 . Требуется построить график функции на интервале значений X [-1; 1].

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Поверхности 2 порядка
МИЭТ, 2020
Проект по компьютерному практикуму
по алгебре и геометрии

История
Ученые, внесшие особый вклад в развитие теории поверхностей второго порядка
Гаспар Монж, 1749-1818
Леонард Эйлер, 1707-1783

Поверхность второго порядка
− геометрическое место точек трёхмерного пространства,
прямоугольные координаты которых удовлетворяют
уравнению вида
𝑨 𝒙 𝟐 +𝑩 𝒚 𝟐 +𝑪 𝒛 𝟐 +𝟐𝑫𝒙𝒚+𝟐𝑬𝒙𝒛+𝟐𝑭𝒚𝒛+𝑮𝒙+𝑯𝒚+𝑳𝒛+𝑺=𝟎
где A, B, C, D не равны одновременно нулю

Уравнение может определять относительно OXYZ вырожденную поверхность (пару плоскостей, точку, пустое множество и т.д.)
Если поверхность невырожденная, то ее уравнение может быть приведено к каноническому виду

Классификация уравнений поверхностей второго порядка

Эллипсоид
𝒙 𝟐 𝒂 𝟐 + 𝒚 𝟐 𝒃 𝟐 + 𝒛 𝟐 𝒄 𝟐 =𝟏
ellipsoid(0,0,0,2,8,5)
[X,Y,Z] = sphere(20);
surf(X,Y,Z)

r = 5;
X2 = X * r;
Y2 = Y * r;
Z2 = Z * r;
surf(X2+5,Y2-5,Z2)

[X,Y,Z] = ellipsoid(x0,y0,z0,xr,yr,zr)
[X,Y,Z] = sphere(N),
N – количество граней

Гиперболоид
однополостный
𝑥 2 𝑎 2 + 𝑦 2 𝑏 2 − 𝑧 2 𝑐 2 =1
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;c=1;
V = (X.^2)./(a^2) + (Y.^2)./(b^2) - (Z.^2)/(c^2);
p=patch(isosurface(X,Y,Z,V,5));
set(p,'FaceColor','red','EdgeColor','none');
view(3);
grid on
camlight
patch(X,Y,Z,C) создает полигоны в трехмерных координатах с помощью X,Y, и Z
Трехмерный массив - объемные данные

Гиперболоид
двуполостный
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;c=1;
V = (X.^2)./(a^2) + (Y.^2)./(b^2) - (Z.^2)/(c^2);
p=patch(isosurface(X,Y,Z,-V,1));
set(p,'FaceColor’, 'red’, 'EdgeColor','none');
view(3);
grid on
camlight

𝑥 2 𝑎 2 + 𝑦 2 𝑏 2 − 𝑧 2 𝑐 2 =−1

Конус
второго порядка
t = [-0.3;0.3];
[X,Y,Z] = cylinder(t,100);
s=surf(X,Y,Z);
alpha(.2)
axis equal

𝑥 2 𝑎 2 + 𝑦 2 𝑏 2 − 𝑧 2 𝑐 2 =0

Параболоид
эллиптический
a=16;
b=16;
[X,Y]=meshgrid(-a:0.1:a,-b:0.1:b);
Z=(X.^2/a^2 +Y.^2/b^2 );
mesh(X,Y,Z);
xlabel('x'), ylabel('y'),zlabel('z')
colormap(pink)
colorbar

Параболоид
гиперболический
a=16;b=16;
[X,Y]=meshgrid(-a:0.1:a,-b:0.1:b);
Z=(X.^2/a^2 -Y.^2/b^2 );
mesh(X,Y,Z)
xlabel('x'),ylabel('y'),zlabel('z')
colormap(pink)
colorbar

Пара пересекающихся плоскостей
𝑥 2 𝑎 2 + 𝑦 2 𝑏 2 =0
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;
V = (X.^2)./(a^2) - (Y.^2)./(b^2) - Z.*0;
p=patch(isosurface(X,Y,Z,V,0));
set(p,'FaceColor','red','EdgeColor','none’);
view(3);
axis equal
camlight

Цилиндр
гиперболический
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;
V = (X.^2)./(a^2) - (Y.^2)./(b^2) - 1;
p=patch(isosurface(X,Y,Z,V,0));
set(p,'FaceColor','red','EdgeColor','none');
view(3);
grid on
camlight

𝑥 2 𝑎 2 + 𝑦 2 𝑏 2 =1
[X,Y,Z] = cylinder(R,N), N – количество граней

Цилиндр
гиперболический
[X,Y,Z] = meshgrid(-10:0.3:10,-10:0.3:10,-10:0.3:10);
a=1;b=1;
V = (X.^2)./(a^2) + (Y.^2)./(b^2) - Z.*1;
p=patch(isosurface(X,Y,Z,V,0));
set(p,'FaceColor','red','EdgeColor','none');
view(3);
grid on
camlight

Цилиндр
параболический
[X,Y,Z] = meshgrid(-20:0.5:20,-20:0.5:20,-20:0.5:20);
p=2;
V = Y.^2-2*p*X;
p=patch(isosurface(X,Y,Z,V,1));
set(p,'FaceColor','m','EdgeColor','none');
view(3);
axis equal, grid on
camlight
𝑦 2 =2𝑝𝑥

Функции для участков поверхностей и сеток

surfс()
[X,Y]=meshgrid([-3:0.1:3]);
Z=sin(X)./(X.^2+Y.^2+0.3);
surfc(X,Y,Z)
– дополнительное построение контурного графика проекции фигуры на опорную плоскость.

[X,Y]=meshgrid([-3:0.1:3]);
Z=sin(X)./(X.^2+Y.^2+0.3);
surfl(X,Y,Z)
colormap(cool)
shading interp
colorbar
- имитирует оптические эффекты рассеивания, отражения и зеркального отражения света
surfl()

contour3(peaks,20)
colormap(pink)
[x,y]=meshgrid(-3:0.1:3);
z=x.^2+y.^2;
contour3 (x,y,z,40)
colormap (bone)
colorbar
contour3()

pcolor()
- отображает матричные данные в виде массива цветных ячеек
C = hadamard(20);
pcolor(C)
colormap(gray(2))
axis ij
axis square
C = [5 13 9 7 12; 11 2 14 8 10; 6 1 3 4 15];
s = pcolor(C);
s.FaceColor = 'interp';
[X,Y] = meshgrid(-3:6/17:3);
XX = 2*X.*Y;
YY = X.^2 - Y.^2;
colorscale = [1:18; 18:-1:1];
C = repmat(colorscale,9,1);
pcolor(XX,YY,C);

Мачты
В начале 20-го века многие боевые корабли в США, строились с ажурными гиперболоидными мачтами.

Причины резкого снижения численности горбуши
31

Проектирование зеркальных и зеркально-оптических систем
Теорема. Отражающие поверхности второго порядка (параболоидальная, эллипсоидальная и гиперболоидальная) характеризуются следующими свойствами:

Двухзеркальные объективы
из асферических поверхностей второго порядка
Объектив Грегори
Объектив Кассегрена
Реверсивный объектив
Принципиальные оптические схемы

Антенны
Антенна Кассегрена: основное параболическое зеркало и гиперболическое вспомогательное зеркало.

Преимущества: небольшие размеры и значительные допуски по размещению излучателя, что способствует появлению разнообразных конструкций антенн

Поверхности 2 порядка как характеристика кристалла и его свойств

Кристаллы низшей категории – двухосные

Их волновая поверхность состоит из частично пересекающихся сфер и эллипсоидов

Выводы
Теория поверхностей второго порядка находит свое применение во многих областях науки и жизни.

Одно из достоинств системы MATLAB — обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов.

Построение графиков отрезками прямых

Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси — горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB — матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера.

Команда plot служит для построения графиков функций в декартовой системе координат. Эта команда имеет ряд параметров, рассматриваемых ниже.

plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Y — матрица, то строится семейство графиков по данным, содержащимся в колонках матрицы.

Приведенный ниже пример иллюстрирует построение графиков двух функций — sin(x) и cos(x), значения функции которых содержатся в матрице Y, а значения аргумента х хранятся в векторе X:

На рисунке показан график функций из этого примера. В данном случае отчетливо видно, что график состоит из отрезков, и если вам нужно, чтобы отображаемая функция имела вид гладкой кривой, необходимо увеличить количество узловых точек. Расположение их может быть произвольным.

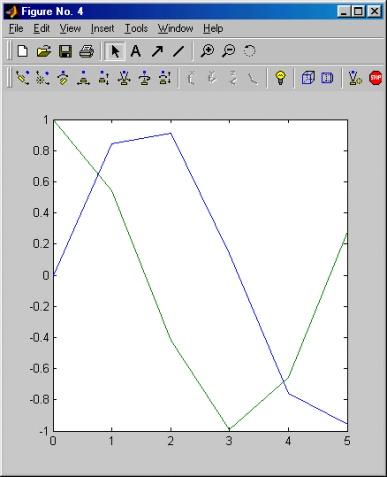
plot(Y) — строит график у(i), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Y содержит комплексные элементы, то выполняется команда plot (real (Y), imag(Y)). Во всех других случаях мнимая часть данных игнорируется.

Вот пример использования команды plot(Y):

Соответствующий график показан на рисунке.

plot(X,Y,S) — аналогична команде plot(X,Y), но тип линии графика можно задавать с помощью строковой константы S.

Построение поверхности с окраской

Особенно наглядное представление о поверхностях дают сетчатые графики, использующие функциональную закраску ячеек. Например, цвет окраски поверхности z(x, у) может быть поставлен в соответствие с высотой z поверхности с выбором для малых высот темных тонов, а для больших — светлых. Для построения таких поверхностей используются команды класса surf (. ):

surf (X, Y, Z. С) — строит цветную параметрическую поверхность по данным матриц X, Y и Z с цветом, задаваемым массивом С;

surf(X.Y.Z) — аналогична предшествующей команде, где C=Z, так что цвет задается высотой той или иной ячейки поверхности;

surf(x.y.Z) и surf(x.y.Z.C) с двумя векторными аргументами х и у — векторы х и у заменяют первых два матричных аргумента и должны иметь длины length(x)=n и length(y)=m, где [m.n]=size(Z). В этом случае вершины областей поверхности представлены тройками координат (x(j), yd), Z(1,j)). Заметим, что х соответствует столбцам Z, а у соответствует строкам;

surf(Z) и surf(Z.C) используют х = 1:n и у = 1:m. В этом случае высота Z — однозначно определенная функция, заданная геометрически прямоугольной сеткой;

h=surf (. ) —строит поверхность и возвращает дескриптор объекта класса surface.

Команды axis, caxis, color-map, hold, shading и view задают координатные оси и свойства поверхности, которые могут использоваться для большей эффектности показа поверхности или фигуры.

Ниже приведен простой пример построения поверхности — параболоида:

Контурные графики

Контурные графики служат для представления на плоскости функции двух переменных вида z(x, у) с помощью линий равного уровня. Они получаются, если трехмерная поверхность пересекается рядом плоскостей, расположенных параллельно друг другу. При этом контурный график представляет собой совокупность спроецированных на плоскость (х, у) линий пересечения поверхности г(х, у) плоскостями.

Для построения контурных графиков используются команды contour:

contour(Z) — строит контурный график по данным матрицы Z с автоматическим заданием диапазонов изменения х и у;

contour(X, Y, Z) — строит контурный график по данным матрицы Z с указанием спецификаций для X и Y;

contour(Z, N) и contour(X, Y, Z, N) — дает построения, аналогичные ранее описанным командам, с заданием N линий равного уровня (по умолчанию N=10);

contour(Z, V) и contour(X, Y, Z, V) — строят линии равного уровня для высот, указанных значениями элементов вектора V;

contour(Z, [v v]) или contour(X, Y, Z, [v v]) — вычисляет одиночный контур для уровня v;

[С, Н] = contour (. ) — возвращает дескрипторы — матрицу С и вектор-столбец Н. Они могут использоваться как входные параметры для команды clabel;

contour(. 'LINESPEC') — позволяет использовать перечисленные выше команды с указанием спецификации линий, которыми идет построение.

Пример построения контурного графика поверхности, заданной функций peaks:

Построенный в этом примере график показан на рисунке. Заметим, что объект — функция peaks — задан в MATLAB в готовом виде.

Создание массивов данных для трехмерной графики

Трехмерные поверхности обычно описываются функцией двух переменных z(x, у). Специфика построения трехмерных графиков требует не просто задания ряда значений х и у, то есть векторов х и у. Она требует определения для X и Y двумерных массивов — матриц. Для создания таких массивов служит функция meshgrid. В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция meshgrid записывается в следующих формах:

[X, Y] = meshgrid(x) — аналогична [X, Y] = meshgrid(x.x);

[X, Y, Z] = meshgrid(x, y, z) — возвращает трехмерные массивы, используемые для вычисления функций трех переменных и построения трехмерных графиков;

[X, Y] = meshgrid(x, y) — преобразует область, заданную векторами х и у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора х; а столбцы Y — копиями вектора у.

Основным является сессионный cookie, обычно называемый MoodleSession. Вы должны разрешить использование этого файла cookie в своем браузере, чтобы обеспечить непрерывность и оставаться в системе при просмотре сайта. Когда вы выходите из системы или закрываете браузер, этот файл cookie уничтожается (в вашем браузере и на сервере).

Другой файл cookie предназначен исключительно для удобства, его обычно называют MOODLEID или аналогичным. Он просто запоминает ваше имя пользователя в браузере. Это означает, что когда вы возвращаетесь на этот сайт, поле имени пользователя на странице входа в систему уже заполнено для вас. Отказ от этого файла cookie безопасен - вам нужно будет просто вводить свое имя пользователя при каждом входе в систему.

Читайте также: