Как сделать последовательность неубывающей последовательностью с минимальным количеством шагов
дана последовательность N целых чисел. На каждом шаге разрешается увеличивать значение любого числа на 1 или уменьшить его на 1. Цель игры состоит в том, чтобы сделать последовательность не убывает с минимальным количеством шагов
можно сделать эту последовательность неубывающая последовательность в 4 -х шагов (3 Уменьшение на 1 и увеличивает -1 на 3).
Как я могу решить эту проблему?
Задан 27/04/2011 в 03:59 2011-04-27 03:59
источник пользователем user467871 На других языках.
Ну проблема гласит, что вы должны стремиться к минимальному количеству изменений. Допустим, что последний номер -1000000. Если вы бежите через последовательность последовательно вы будете в конечном итоге, чтобы добавить 1000002 до последнего элемента, чтобы получить неубывающая последовательность, но решение будет не в состоянии удовлетворить требования, используя минимальное количество шагов. Therefor это может быть хорошей идеей, чтобы запустить через последовательность один раз, запись различия между элементами. Надеюсь, что вы ловите мой дрейф. (Им не ясно, в письменном виде, как мои мысли появляются в моем-я :-)
Внутри GenerateSequenceForCurrentIndex (), значение в левой части индекса удостоверилось равным массив [индекс]. Мы не должны беспокоиться о том, чем меньше, как будет уже позаботилась различными последовательностями (когда индекс 2011-04-27 08:17 share
источник пользователем Sandeep G B
Если вы посмотрите на пузырьковой сортировке, в первом проходе внешнего контура, то поместить элемент в правильном месте, я пытаюсь использовать эту концепцию. как только вы узнаете, первый проход обменивать позицию, использовать его для справки и настроить все элементы в последовательности по отношению к этому элементу.
Вы должны найти последовательность, которая является
- интеграл
- без уменьшения
- а ближе всего, как можно ближе к оригиналу в L ^ 1 нормы .
Это выпуклая задача целочисленной оптимизации при ограничениях , которые , кажется очень трудно решить оптимально.
Я получил следующую мысль:
- Построение групп, не являющихся убывающих последовательностей (в вашем примере 2 11)
- Объединение двух групп, это уменьшает количество групп на один или два.
- Если существует только одна группа, не уменьшая решение найдено. Если нет, вернитесь к шагу 2.
Объединение: Есть всегда две возможности объединения двух групп, настроить левую группу или настроить нужную группу. Я покажу это на примерах, идея должна быть ясна.
Ajust правой группы:
Отрегулируйте левую группу:
Потому что всегда есть два пути (регулировки вправо / влево отрегулируйте группу), вы можете использовать шаги в алгоритме обратного прослеживания (который запоминает лучшее найденное решение до сих пор).
Демонстрация:
Решения:
Обратите внимание, что существует неубывающая последовательность, которая может быть получена из данной последовательности с использованием минимального числа ходов, и в котором все элементы равны некоторый элемент из исходной последовательности (то есть, который состоит только из чисел от исходной последовательности ).
Предположим, что не существует оптимальная последовательность, где каждый элемент равен некоторому элементу из исходной последовательности. Тогда существует элемент я, который не равен ни одному из элементов . Если элементы с номерами I-1 и я + 1 не равно элементу I, то мы можем переместить его ближе к аи, и ответ будет уменьшаться. Таким образом, есть блок равных элементов, и все они не равны ни одному из элементов исходной последовательности. Обратите внимание, что мы можем увеличить весь блок на 1 или уменьшить его на 1 и одно из этих действий не будет увеличиваться ответом, поэтому мы можем переместить этот блок вверх или вниз, пока все ее элементы будут равен некоторый элемент из исходной последовательности.
Пусть является исходная последовательность, является та же последовательность, но в которой все элементы различны, и они сортируются от наименьшего к наибольшему. Пусть F (I, J) минимальное число ходов, необходимых для получения последовательности, в которой первые элементы являются I не убывает и я-й элемент в большинстве Bj. В этом случае ответ на вопрос будет равна F (п, к), где п длина и к является длина . Мы будем вычислять f (I, J), используя следующие рецидивы:
Сложность O (N 2). Для того, чтобы избежать ограничения памяти следует отметить , что для вычисления F (я, ), необходимо только знать F (я-1, ) и часть I-й строки , которая уже вычисленной.
Стандартные види динамики
Включение исходной задачи в семейство зависимых подзадач требует изобретательности, но есть несколько стандартных вариантов. Вот они:
- Вычисляем простую последовательность. Исходную задачу можно включить в вычисление элементов последовательности $x_1, x_2, \ldots, x_n$, подзадачи — вычисление значений $x_i$ для $i \le n$, причём $x_i$ вычисляется на основе фиксированного количества предыдущих членов (как в примере с числами Фибоначчи). Сложность решения — $O(n)$. Пример задачи — числа Фибоначчи и последовательности, заданные рекуррентными соотношениями.
- Вычисляем сложную последовательность. То же самое, что в предыдущем пункте, но $x_i$ вычисляется на основе всех предыдущих членов. Сложность решения — $O(n^2)$. Достаточно часто существует оптимизация решения до $O(n \log n)$;
- Вычисляем две последовательности. Исходную задачу можно включить в вычисление элементов последовательностей $x_1, x_2, \ldots, x_m$ и $y_1, y_2, \ldots, y_n$. Подзадачи — вычисление конкретных $x_i$ и $y_j$. Каждый из $x_i$ и $y_j$ легко вычисляются на основе фиксированного набора предыдущих членов. Сложность решения — $O(mn)$;
- Вычисляем двумерный массив. Исходную задачу можно включить в вычисление элементов прямоугольного массива $x_, x_, \ldots, x_, x_, \ldots, x_$, подзадачи — вычисление конкретных $x_$, причём $x_$ вычисляется на основе фиксированного количества предыдущих членов. Сложность решения — $O(mn)$. Пример задачи — вычисление редакционного расстояния между двумя строками;
- Обрабатываем последовательность. Задача ставится для данной последовательности $x_1, x_2, \ldots, x_n$, подзадачи — та же задача для префиксов $x_1, x_2, \ldots, x_i$, $i
Вводные задачи
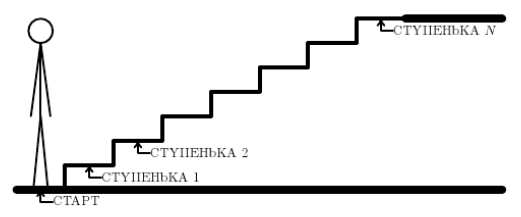
A: Мячик на лесенке
Вводится одно число $0
B: Последовательность из 0 и 1
Требуется подсчитать количество последовательностей длины $N$, состоящих из $0$ и $1$, в которых никакие две единицы не стоят рядом.
На вход программы поступает целое число $N$ $(1 \leqslant N \leqslant 10^5)$.
C: Без трёх единиц
Определите количество последовательностей из нулей и единиц длины $N$ (длина — это общее количество нулей и единиц), в которых никакие три единицы не стоят рядом.
Вводится натуральное число $N$, не превосходящее $40$.
Выведите количество искомых последовательностей. Гарантируется, что ответ не превосходит $2^-1$.
D: Платная лестница
Мальчик подошел к платной лестнице. Чтобы наступить на любую ступеньку, нужно заплатить указанную на ней сумму. Мальчик умеет перешагивать на следующую ступеньку, либо перепрыгивать через ступеньку. Требуется узнать, какая наименьшая сумма понадобится мальчику, чтобы добраться до верхней ступеньки.
В первой строке входного файла вводится одно натуральное число $N \leqslant 100$ — количество ступенек. В следующей строке вводятся $N$ натуральных чисел, не превосходящих $100$ — стоимость каждой ступеньки (снизу вверх).
Выведите одно число — наименьшую возможную стоимость прохода по лесенке.
Одномерное динамическое программирование
E: Радиоактивные материалы
При переработке радиоактивных материалов образуются отходы трех видов — особо опасные (тип A ), неопасные (тип B ) и совсем не опасные (тип C ). Для их хранения используются одинаковые контейнеры. После помещения отходов в контейнеры последние укладываются вертикальной стопкой. Стопка считается взрывоопасной, если в ней подряд идет более одного контейнера типа A . Стопка считается безопасной, если она не является взрывоопасной.
Для заданного количества контейнеров $N$ определить число безопасных стопок.
На вход программе подаётся одно число $1 \leqslant N \leqslant 10^5$.
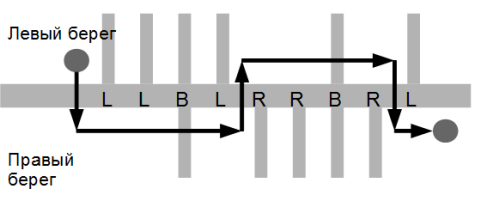
F: Поход вдоль реки
Дети пошли в поход вдоль реки. Поход начинается на левом берегу, заканчивается на правом. Дана последовательность букв 'L', 'R', 'B', означающая с какой стороны в реку впадает приток: 'L' -- слева (left), 'R' -- справа (right), 'B' -- с обеих сторон (both). Определить минимальное количество переправ, которое придётся сделать школьникам.
На вход программа получает строку, содержащую только символы R, L, B в произвольном порядке. Длина строки не превосходит $10^5$ символов.
Выведите одно целое число — минимальное количество переправ.
G: Гвоздики
В дощечке в один ряд вбиты гвоздики. Любые два гвоздика можно соединить ниточкой. Требуется соединить некоторые пары гвоздиков ниточками так, чтобы к каждому гвоздику была привязана хотя бы одна ниточка, а суммарная длина всех ниточек была минимальна.
В первой строке входных данных записано число $N$ — количество гвоздиков $(2 \leqslant N \leqslant 100)$. В следующей строке заданы $N$ неотрицательных целых чисел, не превосходящие $10000$ — координаты всех гвоздиков в порядке возрастания.
Выведите единственное число — минимальную суммарную длину всех ниточек.
H: Покупка билетов
Однако для борьбы со спекулянтами кассир продавала не более $3$-х билетов в одни руки, поэтому договориться таким образом между собой могли лишь $2$ или $3$ подряд стоящих человека.
Известно, что на продажу $i$-му человеку из очереди одного билета кассир тратит $A_i$ секунд, на продажу двух билетов — $B_i$ секунд, трех билетов — $C_i$ секунд. Напишите программу, которая подсчитает минимальное время, за которое могли быть обслужены все покупатели.
Обратите внимание, что билеты на группу объединившихся людей всегда покупает первый из них. Также никто в целях ускорения не покупает лишних билетов (то есть билетов, которые никому не нужны).
На вход программы поступает сначала число $N$ — количество покупателей в очереди $(1 \leqslant N \leqslant 5000)$. Далее идет $N$ троек натуральных чисел $A_i, B_i, C_i$. Каждое из этих чисел не превышает $3600$. Люди в очереди нумеруются, начиная от кассы.
Требуется вывести одно число — минимальное время в секундах, за которое могли быть обслужены все покупатели.
I: Калькулятор с восстановлением ответа
Имеется калькулятор, который выполняет три операции:
- 1. прибавить к числу $X$ единицу;
- 2. умножить число $X$ на $2$;
- 3. умножить число $X$ на $3$;
Выведите строку, состоящую из цифр 1 , 2 или 3 , обозначающих одну из трех указанных операций, которая получает из числа $1$ число $N$ за минимальное число операций. Если возможных минимальных решений несколько, выведите любое из них.
Операторы внутри цикла (что нужно повторить) пишут с отступом.
4 раза напечатать Hello:
for переменная in последовательность : - это оператор python, который перебирает по 1 элементу из последовательности и записывает ее в переменную.
x - имя переменной. Может быть любое.
range - функция python. Она возвращает последовательность целых чисел.
Не забудьте поставить двоеточие :
range(4) вернет последовательность из 0, 1, 2, 3. То есть 4 целых числа, от 0 (включая) до 4 (не включая).
Чтобы напечатать эти числа в 1 строку, будем ставить после каждого числа пробел. В функции print укажем end=' ' (в конце ставить пробел, а не символ новой строки, как обычно).
Функция range(3, 10) вернет последовательность чисел от 3 (включая) до 10 (НЕ включая):
Третий аргумент функции range - на сколько увеличить число: Функция range(3, 10, 2) вернет последовательность чисел от 3 (включая) до 10 (НЕ включая) +2 каждый раз:
читаем и печатаем много чисел
Даны 2 целых числа. 1 число на 1 строке. Нужно прочитать эти числа и напечатать их.
Если числа заданы на одной строке через пробел, то их читаем так:
Похоже можно прочитать много чисел на строке через пробел:
Разберем этот код:
- input() - прочитать строку '3 5 -2 7 1'
- input().split() - разбить прочитанную строку по пробельным символам на строки, получится список строк; ['3', '5', '-2', '7', '1']
- map(функция, последовательность) - применить функцию к каждому элементу последовательности, вернуть полученную последовательность. Тут получили последовательность чисел 3 5 -2 7 1. Переменная a ссылается на эту последовательность.
К полученной последовательности можно применить оператор for..in
Генераторы - 1 раз
Генераторы - это последовательности, по которым можно пройти только один раз.
Если нужно будет пройти по тем же данным несколько раз, их нужно сохранить в памяти. Например, сделать из последовательности map список list.
:question: Зачем нужны последовательности map? Давайте сразу из map делать list.
Список хранит все свои элементы в памяти. Элементы последовательности могут вычисляться только тогда, когда потребуются ("ленивые вычисления") и не занимать место в памяти. Полезно, если элементов очень много.
Еще один пример последовательностей, которые хранятся полностью в памяти - строки.
Рассмотрим простые алгоритмы, которые в 1 проход по последовательности чисел вычисляют то, что требуется в задаче.
Сумма
Дано несколько целых чисел на 1 строке через пробел. Найти сумму этих чисел.
Сумму можно найти в один проход по последовательности чисел.
Рассмотрим более простую задачу: найдем сумму чисел 3, 7, -2:
Если чисел много, то трудно придумывать имена переменных для каждого числа. Перепишем этот код так, чтобы использовать только 2 переменных. res - сумма, x - очередное слагаемое (а не первое слагаемое).
Видно, что есть код, который повторяется. Сделаем из него цикл.
Код, который делаем 1 раз, пишем или до или после цикла.
Будем вводить числа с клавиатуры. Все числа на 1 строке через пробел.
Заметьте, этот код находит сумму любого количества чисел в строке, а не только 3 чисел.
Как мы придумали такой алгоритм?
Представим, что мы уже посчитали сумму последовательности чисел и она хранится в res . Если к последовательности добавить еще одно число (запишем его в x ), то сумма всех чисел станет res = res + x . То есть на каждом шаге цикла нужно прочитать еще одно число и добавить его к сумме.
Чему должны быть равны значения переменных ДО цикла? Представим, что чисел еще нет. Тогда их сумма 0. x до цикла нам не нужен (чисел нет). res до цикла 0.
Запишем этот алгоритм как функцию mysum от последовательности. Функция будет возвращать сумму чисел.
Заметим, что функция может находить сумму последовательности любых чисел, а не только целых чисел.
Максимум
Дана последовательность чисел. Найдем максимальное число.
Сначала напишем функцию max2(x, y) , которая из двух чисел возвращает максимальное.
Будем думать как в алгоритме с суммой.
Пусть мы нашли максимальное число для последовательности и сохранили его в res . Нам дали еще одно число в переменной x . Тогда максимум из всех чисел - это максимум из res и x . То есть max2(res, x) .
Проверяем, как работает программа:
Проверим еще раз на последовательности отрицательных чисел.
Программа работает неправильно. Максимум из отрицательных чисел не может быть 0.
Мы не подумали, чему равен максимум, если чисел нет или оно одно. Если чисел еще нет, то сумма 0, если задано одно число, то сумма равна этому числу.
Если числа не заданы. Максимума у последовательности нет. А у нас в коде написано res = 0 . Ошибка.
Если задано одно число, то это число - миниумум.
Надо научиться писать значение "не число" или брать из последовательности первый элемент.
В Python есть специальное значение None - "этого значения нет".
Посмотрим в интерпретаторе, как раборать с None :
is None и is not None - правильные проверки на None.
Если х не None, то результаты проверок:
Перепишем программу, которая находит максимум, через None:
Проверяем, как работает программа:
next(a) - функция языка питон, возвращает следующий элемент в последовательности.
Пусть последовательность - это числа 5, 12, -1. Переберем ее значения, используя функцию next.
Когда значения в последовательности закончились, функция next не смогла вернуть элемент, и кинула исключение StopIteration . Исключения мы изучим позже.
Перепишем программу поиска максимума через next:
Перепишем программу, которая находит максимум, через None:
Проверяем, как работает программа:
Заметим, что перебирать в for .. in мы начали с числа -7. Число -2 мы взяли из последовательности раньше.
Даны целые числа. Есть ли среди них число 5?
Если числа 5 нет, то нужно перебрать все числа, чтобы узнать это.
Если число 5 нашли, то дальше перебирать не нужно. Мы уже нашли число.
break - закончить цикл (перейти за конец цикла)
Проверим, как работет программа:
Заметим, мы закончили работать на первом числе 5 и следующие числа не печатали.
В for . else и while . else часть в else работает, если в цикле не работал break.
Учитывая входную последовательность, наилучший способ найти самую длинную (не обязательно непрерывную) неубывающую подпоследовательность.
Я ищу лучший алгоритм. Если есть код, Python будет приятным, но все в порядке.
ОТВЕТЫ
Ответ 1
Я просто наткнулся на эту проблему и придумал реализацию Python 3:
Поскольку мне потребовалось некоторое время, чтобы понять, как работает алгоритм, я был немного многословен с комментариями, и я также добавлю краткое объяснение:
- seq - входная последовательность.
- L - это число: оно обновляется во время цикла по последовательности и отмечает длину самой длинной включающей подпоследовательности, найденной до этого момента.
- M это список. M[j-1] будет указывать на индекс seq который содержит наименьшее значение, которое можно использовать (в конце) для построения возрастающей подпоследовательности длины j .
- P это список. P[i] будет указывать на M[j] , где i - индекс seq . В нескольких словах он говорит, какой из предыдущих элементов подпоследовательности является. P используется для построения результата в конце.
Как работает алгоритм:
- Обработайте особый случай пустой последовательности.
- Начните с подпоследовательности 1 элемента.
- Цикл по входной последовательности с индексом i .
- С помощью бинарного поиска найти j , которые позволяют seq[M[j] быть чем seq[i] .
- Обновите P , M и L
- Проследите результат и верните его в обратном порядке.
Примечание. Единственными отличиями в алгоритме википедии являются смещение 1 в списке M и то, что X здесь называется seq . Я также протестировал его с немного улучшенной версией тестового модуля, которая была показана в ответе Эрика Густавсона, и она прошла все тесты.
В конце мы будем иметь:
Как вы увидите, P довольно прост. Мы должны смотреть на это с конца, поэтому он говорит, что до 60 там 40, до 80 там 40 , до 40 там 20 , до 50 там 20 и до 20 там 10 , остановись.
Сложная часть на M В начале M было [0, None, None. ] так как последний элемент подпоследовательности длины 1 (следовательно, позиция 0 в M ) был с индексом 0: 30 .
На данный момент мы начнем зацикливание на seq и посмотреть на 10 , так как 10 составляет чем 30 , M будет обновлен:
Теперь M выглядит так: [1, None, None. ] . Это хорошо, потому что у 10 больше каналов, чтобы создать длинную увеличивающуюся подпоследовательность. (Новый 1 - индекс 10)
Теперь очередь за 20 . С 10 и 20 у нас есть подпоследовательность длины 2 (индекс 1 в M ), поэтому M будет: [1, 2, None. ] . (Новый 2 - это индекс 20)
Теперь очередь за 50 . 50 не будет частью какой-либо подпоследовательности, поэтому ничего не меняется.
Теперь очередь за 40 . С 10 , 20 и 40 у нас есть подпункт длины 3 (индекс 2 в M , поэтому M будет: [1, 2, 4, None. ] . (Новый 4 - это индекс 40)
Для полной прогулки по коду вы можете скопировать и вставить его здесь :)
Ответ 2
Вот как просто найти самую длинную возрастающую/уменьшающуюся подпоследовательность в Mathematica:
Mathematica также выполняет LongestIncreasingSubsequence в библиотеке Combinatorica`. Если у вас нет Mathematica, вы можете запросить WolframAlpha.
Решение С++ O (nlogn)
Также существует решение O (nlogn), основанное на некоторых наблюдения. Пусть Ai, j - наименьший возможный хвост из всех увеличивающихся подпоследовательности длины j, используя элементы a 1, a 2. a i. Обратите внимание, что для любого конкретный i, A i, 1, A i, 2. A i, j. Это говорит о том, что если нам нужна самая длинная подпоследовательность заканчивается ai + 1, нам нужно только посмотреть для j j таких, что Ai, j < 1, 9, 3, 8, 11, 4, 5, 6, 4, 19, 7, 1, 7 >и ответ: 1 3 4 5 6 7 .
Ответ 3
Вот довольно общее решение, которое:
- работает в O(n log n) время,
- обрабатывает увеличивающиеся, неубывающие, убывающие и невозрастающие подпоследовательности,
- работает с любыми объектами последовательности, включая list , numpy.array , str и более,
- поддерживает списки объектов и пользовательские методы сравнения с помощью параметра key , который работает как функция встроенной функции sorted ,
- может возвращать элементы подпоследовательности или их индексы.
Я написал docstring для функции, которую я не вставлял выше, чтобы показать код:
Этот ответ частично был вдохновлен вопросом в обзоре кода и частично вопросом, спрашивающим о "из последовательности" .
Ответ 4
Вот некоторый код python с тестами, которые реализуют алгоритм, выполняющийся в O (n * log (n)). Я нашел это на странице wikipedia о самой длинной растущей подпоследовательности.
Ответ 5
Ответ 6
Вот код и объяснение с Java, возможно, я скоро добавлю для python.
- list = - Инициализировать список до пустого набора
- list = - новый LIS
- list = - Изменено 8 до 4
- list = - Новый LIS
- list = - Изменено с 4 по 2
- list = - Изменено от 12 до 10
- list = - Изменено от 10 до 6
- list = - новый LIS
- list = - Изменено 2 к 1
- list = - Изменено с 14 по 9
- list = - Изменено 6 - 5
- list = - Изменено 3 до 2
- list = - Новый LIS
- list = - Изменено с 9 по 5
- list = - Новый LIS
- list = - новый LIS
Таким образом, длина LIS равна 6 (размер списка).
Вывод для приведенного выше кода: Наибольшее увеличение подпоследовательности [0, 1, 3, 7, 11, 15]
Ответ 7
Самый эффективный алгоритм для этого - O (NlogN), обозначенный здесь.
Еще один способ решить эту задачу - взять самую длинную общую подпоследовательность (LCS) исходного массива и отсортированную версию, которая принимает O ( N 2 ).
Ответ 8
здесь реализована компактная реализация с использованием "enumerate"
Ответ 9
Здесь более компактная, но все же эффективная реализация Python:
Ответ 10
Мы будем использовать последовательность 2, 8, 4, 12, 3, 10, и, чтобы было легче следовать, нам потребуется, чтобы входная последовательность не была пустой и не включала одно и то же число более одного раза.
Проходим последовательность по порядку.
Как мы делаем, мы поддерживаем набор последовательностей, лучшие последовательности, которые мы до сих пор нашли для каждой длины. После того, как мы находим первую последовательность длины 1, которая является первым элементом входной последовательности, мы гарантированно получим набор последовательностей для каждой возможной длины от 1 до самой длинной, которую мы до сих пор нашли. Это очевидно, потому что если у нас есть последовательность длины 3, то первые 2 элемента этой последовательности являются последовательностью длины 2.
Итак, мы начинаем с первого элемента, представляющего собой последовательность длины 1, и наш набор выглядит следующим образом:
Мы берем следующий элемент последовательности (8) и ищем самую длинную последовательность, к которой мы можем добавить его. Это последовательность 1, поэтому мы получаем
Мы берем следующий элемент последовательности (4) и ищем самую длинную последовательность, к которой мы можем добавить его. Самая длинная последовательность, к которой мы можем добавить ее, это длина 1 (всего 2 ). Вот то, что я нашел, хитрая (или, по крайней мере, неочевидная) часть. Поскольку мы не можем добавить его в конец последовательности длины 2 ( 2 8 ), это означает, что должен быть лучший выбор для завершения кандидата длины 2. Если бы элемент был больше 8, он бы привязался к последовательности длины 2 и дал бы нам новую последовательность длины 3. Итак, мы знаем, что это меньше, чем 8, и поэтому заменим 8 на 4.
С точки зрения алгоритма, мы говорим, что независимо от того, какую самую длинную последовательность мы можем прикрепить к элементу, эта последовательность плюс этот элемент является наилучшим кандидатом на последовательность результирующей длины. Обратите внимание, что каждый элемент, который мы обрабатываем, должен где-то принадлежать (потому что мы исключили повторяющиеся числа во входных данных). Если он меньше, чем элемент длиной 1, это новая длина 1, в противном случае он идет в конце некоторой существующей последовательности. Здесь последовательность длины 1 плюс элемент 4 становится новой последовательностью длины 2, и мы имеем:
Следующий элемент, 12, дает нам последовательность длины 3, и мы имеем
Следующий элемент, 3, дает нам лучшую последовательность длины 2:
Обратите внимание, что мы не можем изменить последовательность длины 3 (подставляя 3 вместо 4), потому что они не встречались в указанном порядке во входной последовательности. Следующий элемент, 10, заботится об этом. Поскольку лучшее, что мы можем сделать с 10, это добавить его к 2 3 это становится новым списком длины 3:
Обратите внимание, что с точки зрения алгоритма нам действительно все равно, что предшествует последнему элементу в любой из наших последовательностей-кандидатов, но, конечно, нам необходимо отслеживать, чтобы в конце мы могли вывести полную последовательность.
Мы продолжаем обрабатывать входные элементы следующим образом: просто прикрепляем каждый из них к самой длинной последовательности, которую мы можем, и делаем эту новую последовательность-кандидат для полученной длины, потому что она гарантированно не будет хуже существующей последовательности этой длины. В конце мы выводим самую длинную последовательность, которую мы нашли.
Оптимизации
Одна оптимизация заключается в том, что нам не нужно хранить всю последовательность каждой длины. Для этого потребовалось бы место O (n ^ 2). По большей части мы можем просто сохранить последний элемент каждой последовательности, поскольку это все, с чем мы когда-либо сравнивали. (Я покажу, почему этого не совсем достаточно, чуть позже. Посмотрим, сможете ли вы выяснить, почему, прежде чем я доберусь до этого.)
Допустим, мы будем хранить наш набор последовательностей в виде массива M где M[x] содержит последний элемент последовательности длины x . Если вы подумаете об этом, вы поймете, что элементы M сами в порядке возрастания: они отсортированы. Если бы M[x+1] было меньше, чем M[x] , он бы заменил M[x] .
Поскольку M сортируется, следующая оптимизация переходит к тому, что я полностью затмил выше: как нам найти последовательность для добавления? Ну, так как M отсортировано, мы можем просто выполнить бинарный поиск, чтобы найти самое большое M[x] меньше, чем добавляемый элемент. Это последовательность, к которой мы добавляем.
Это замечательно, если все, что мы хотим сделать, это найти длину самой длинной последовательности. Однако M недостаточно для восстановления самой последовательности. Помните, однажды наш набор выглядел так:
Мы не можем просто вывести сам M как последовательность. Нам нужно больше информации, чтобы иметь возможность восстановить последовательность. Для этого мы делаем еще 2 изменения. Во-первых, мы сохраняем входную последовательность в массиве seq и вместо того, чтобы хранить значение элемента в M[x] , мы сохраняем индекс элемента в seq , поэтому значение seq[M[x]] .
Мы делаем это так, чтобы мы могли вести учет всей последовательности, связывая подпоследовательности. Как вы видели в начале, каждая последовательность создается путем добавления одного элемента в конец уже существующей последовательности. Итак, во- вторых, мы сохраняем другой массив P котором хранится индекс (в seq ) последнего элемента последовательности, к которой мы добавляем. Чтобы сделать его цепным, поскольку то, что мы храним в P является индексом seq мы должны индексировать сам P по индексу seq .
Это работает так, что при обработке элемента i из seq мы находим последовательность, к которой добавляем. Помните, мы собираемся прикрепить seq[i] к последовательности длины x чтобы создать новую последовательность длины x+1 для некоторого x , и мы сохраняем i , а не seq[i] в M[x+1] . Позже, когда мы обнаружим, что x+1 - наибольшая возможная длина, мы захотим восстановить последовательность, но единственной отправной точкой, которую мы имеем, является M[x+1] .
То, что мы делаем, это устанавливаем M[x+1] = i и P[i] = M[x] (что идентично P[M[x+1]] = M[x] ), то есть для каждый элемент i мы добавляем, мы сохраняем i как последний элемент в самой длинной цепочке, которую мы можем, и мы сохраняем индекс последнего элемента цепочки, который мы расширяем, в P[i] . Итак, мы имеем:
И теперь мы закончили. Если вы хотите сравнить это с реальным кодом, вы можете посмотреть другие примеры. Основное различие заключается в том, что они используют j вместо x , могут хранить список длины j в M[j-1] вместо M[j] чтобы не тратить пространство на M[0] , и могут вместо этого вызывать входную последовательность X seq .
Ответ 11
Вот мое C++ решение проблемы. Решение проще, чем все представленные здесь, и оно быстрое: N*log(N) алгоритмическая сложность времени. Я отправил решение на leetcode, оно работает 4 мс, быстрее, чем 100% представленных решений C++.

Идея (на мой взгляд) ясна: пересечь заданный массив чисел слева направо. Поддерживать дополнительно массив чисел ( seq в моем коде), который содержит возрастающую подпоследовательность. Когда взятое число больше всех чисел, содержащихся в подпоследовательности, поместите его в конец seq и увеличьте счетчик длины подпоследовательности на 1. Когда число меньше наибольшего числа в подпоследовательности, поместите его в любом случае в seq , в том месте, где он должен хранить подпоследовательность, отсортированную путем замены некоторого существующего числа. Подпоследовательность инициализируется длиной массива исходных чисел и начальным значением -inf, что означает наименьшее целое число в данной ОС.
вот как меняется последовательность, когда мы пересекаем числа слева направо:
Самая длинная возрастающая подпоследовательность для массива имеет длину 4.
Ну, пока все хорошо, но как мы узнаем, что алгоритм вычисляет длину самой длинной (или одной из самых длинных, здесь может быть несколько подпоследовательностей одинакового размера) подпоследовательности? Вот мое доказательство:
Предположим, что алгоритм не вычисляет длину самой длинной подпоследовательности. Тогда в исходной последовательности должно существовать число, такое, что алгоритм пропущен, и это сделает подпоследовательность более длинной. Допустим, для подпоследовательности x 1, x 2. x n существует такое число y, что x k & lt; у & lt; x k + 1, 1 & lt; = k & lt; = n. Чтобы внести вклад в подпоследовательность, y должен находиться в исходной последовательности между x k и x k + 1. Но тогда мы имеем противоречие: когда алгоритм пересекает исходную последовательность слева направо, каждый раз, когда он встречает число, большее, чем любое число в текущей подпоследовательности, он расширяет подпоследовательность на 1. К тому времени, когда алгоритм встретит такое число y, подпоследовательность будет иметь длину k и содержать числа x 1, x 2. x k. Потому что x k & lt; y, алгоритм расширит подпоследовательность на 1 и включит y в подпоследовательность. Та же логика применяется, когда у - наименьшее число подпоследовательности, расположенное слева от x 1 или когда у - наибольшее число подпоследовательности и расположенное справа от x n. Вывод: такого числа у не существует и алгоритм вычисляет самую длинную возрастающую подпоследовательность. Я надеюсь, что это имеет смысл.
В заключительном утверждении я хотел бы отметить, что алгоритм может быть легко обобщен для вычисления самой длинной убывающей подпоследовательности для любых типов данных, элементы которых можно упорядочить. Идея та же, вот код:
Читайте также: