Как сделать плюс 2
Это не юмор, а просто попытка увидеть рассуждения разных людей по такому элементарному вопросу.
Поэтому пожалуйста пишите небольшие коменты под вашим ответом.
Оценить 6 комментариев
Приоритет операций:
скобки
умножение/деление (слева направо)
сложение/вычитание (слева направо)
Соответственно
6/2(1+2)
1. 6/2*3
2. 3*3
3. 9
Не получается.
Хорошо, напишу вот так: ПРИОРИТЕТ ОПЕРАЦИЙ. Так понятнее?
6:2*(1+2) = 6:2*3 = 3*3 = 9
Реформа Фурсенки в действии :(
Dolios, вы ошибаетесь. Как не посмотри на этот пример: хоть с точки зрения арифметики, хоть с точки зрения алгебры; запись некорректная, у данного примера ответа нет. Если это пример из арифметики, то перед скобками надо было обязательно ставить знак умножения, если это алгебра, то не понятно - это 6/2 забыли в скобки заключить или все таки 6 надо разделить на все выражение 2(1+2)?
Что, *лядь, за ересь тут в комментариях? Хабр высокообразованный интеллектуальный народ. Считать не умеют. ппц, слов нет. В школе не учились? Когда перед скобками нет знака — это умножение. Сначала выполняется операция в скобках. Операции умножения и деление равнозначны по приоритету.
Так громко кричать и самому же писать ересь. Да ответ верный, но ход решения неправильный.
В математике, когда перед скобками стоит умножение, то мы должны опускать скобки, а не умножать на них. Формула a*(b+c) = a*b+a*c.. И применив к уравнению получим 6/2 =3 после опускаем скобки 3*1+3*2 = 9
Но то что вы написали это грубая ошибка.
an_tropa: Математика такая многогранная и позволяет делать действия, не противоречащее правилам как душе угодно. Захочу умножу всё на 2 для удобства, а потом в конце разделю на это же число. Но у меня волосы дыбом встают от ваших высказываний.
Слышали про школьное правило "Действия, заключенные в скобки, выполняются раньше других"?
В математике нет деления как и вычитания, есть умножение на обратное число и сложение отрицательных чисел. И в этом примерно не понятно, это 6 умножается на 1/2 или же на 1/(2(1+2))? Запись некорректна даже с точки зрения арифметики, знак перед скобками в арифметике всегда прописывается. Нет ответа у данного выражения
Рассказываю почему.
Вот картинка с двумя вариантами как кто видит формулу итоговую:
Кто считает, что первый вариант верен — получите в итоге 9.
Кто считает, что верен второй вариант — получат в итоге 1.
Но по правилам, раз 6/2 не заключено в скобки, значит всё что после дроби — находится в знаменателе, значит верен второй вариант.

Покажите пожалуйста, где описаны такие правила. Умножение и деление по приоритетам идентичны. Выполняются слева направо. Соответственно сначала 6/2, а потом результат умножаем на 3.

У меня сразу получилась 1, со школы помню что дробь имеет более высокий приоритет (вот в таких ситуациях).
Тут уже как воспринимать.
Деление часто показывается двоеточием.
Пример
Поэтому тут и правда — кого как учили, то так знак "/" и воспринимает. Кто-то как дробь, потому как деление — знак ":", а для кого-то "/" — знак деления, тогда, правда, формулы усложняются — приходится больше скобок настраивать.
Тут уже дело не вкуса, а обучения в школе ;-).

Так что, для тех, кто хорошо учился в советской школе 6:2(1+2) = 1
Очень занятное наблюдение на приведённом скриншоте ". поэтому знак умножения опускается. " и в примере тут же пример СО знаком. Получается, что всёё наоборот? Ахрана, атмена?)

EugeneOZ, что-то не могу понять как вы дробь горизонтально запишете в текстовом редакторе. Можете пример привезти?
Если принимать слеш как дробь, а двоеточие как деление, то вот пара примеров.
Вариант 1.
6/2(1+2)
Если же Принимать слеш как деление — то как обозначать дробь? Только добавлять скобки, увеличивая формулу в габаритах.
То есть 6/(2(1+2))
А когда имеешь дело с кучей скобок (это в этом примере всего одни вложенные — а когда их с десяток?) — легче ошибиться. Кто учился на инженера в ВУЗе меня поймёт.
я сначала все что в скобках на 2 домножила, потом 6 поделила на 2 и прибавила 4. вот: 6÷2(1+2)=6÷(2*1)+(2*2)=6÷2+4=3+4=7
Oh my God, и это сайт программистов! Какой нахрен "1", вы хотя бы в Excel проверьте это выражение, если своих мозгов не хватает. Правильный ответ "9".
Расшифровка: 6/2(1+2) =?
6/2*(3).
Заметьте, не 6/(2*3), а именно 6/2*3. Дальше за вас посчитать?
Надо эту задачу на собеседовании давать, чтобы идиотов отсеивать сразу.
для того чтобы что то делить, нужно что то получить, поэтому умножение в приоретете
правильный ответ 1

Такое предложение решить легко, если знать порядок действий в математике. Правильный порядок арифметических действий в математике зависит от их типа и условий конкретного примера. Знание правил очередности необходимо, поскольку они являются основой как для многих бытовых операций (покупки, измерения), так и более сложных расчетов.
Правильный ответ 9. Дробь есть деление числителя на знаменатель. Но само деление по сути не есть дробь). А так как дробь это чисто горизонтальная черта а не деление, то ответ именно 9.Кто думает иначе тот скорее всего переучился))).

Во-первых ":" = "/" = дробная черта. Это все одно и то же действие. Правильный ответ 9. 6:2(2+1) = 6:2*3 = 6:2 * 3:1. Умножение дробей. 3 окажется в знаменателе только в случае 6:(2*3), иначе она в числителе. Кто считает иначе - учебник в руки.
Вы читали свой ответ? Ничего не понятно, что вы хотели сказать. У этого примера в такой записи ответа нет. Запись некорректна.
Строго говоря в метематике нет деления, есть умножение на обратное число. Так здесь не понятно обратное число 1/2 или 1/(2(2+1))? И что хотел записать автор (6/2)*(2+1) или 6/(2(2+1)) неясно
Да как же вы задолбали. Пропуск знака умножения - это то же самое, что внешние скобки
6:2(2+1) = 6:(2*(2+1)), но никак не 6:2*(2+1)
А вот что в Маткаде получается


6÷2(1+2)=7 Для решения этого примера использую основные правила: 1. Освобождаемся от скобок. 2. Выполняе
м действия согласно первоочередности. Рассмотрим два примера: 6÷2(1+2)=9 школьная программа по арифметики: освобождение от скобок производим путем действия в скобках (1+2=3) далее 6÷2=3. 3×3=9. Другой пример: 6÷2(a+b)= где a=1. b=2. Освобождение от скобок путем действием в скобках (a+b=?).Другой способ освобождения от скобок это раскрываем скобки. 6÷2(a+b)=6÷2a+2b этот способ применяем в первом примере 6÷2(1+2)=6÷2+4=7. Отсюда следует,если действия применимы в больших вариантах,то они наиболее правильные!? 6÷2(1+2)=6÷2+4=7 Спасибо. Ps. для меня кофе всегда он.
Извиняюсь но у вас бред,
6/2(а+б)=6/(2а+2б)
Скобки не открываются пока не решится сума
Поэтому ваш второй вариант
6/2(1+2)=6/(1×2+2×2)=6/(2+4)=6/6=1
Извиняюсь, но у вас бред по-хуже.
Если вносить под скобки, то никак не 6/(2а+2б)
6/2 - это дробь, если учитывать порядок действий, ее можно представлять хоть в виде 12/2/2, хоть в виде 48/2/2/2/2
А если идти тем путем, о чем вы тут пишете, то это выглядит так ((6/2)а+(6/2)б) = 3а+3б = 3*1 + 3*2 = 3 + 6 и верный ответ, как ни крути = 9.
Тут кто правила сам придумает, а кто-то просто не знает правил, делая ошибку, и доказывает свою точку зрения, надеюсь достаточно мелко разжевал.
6/2(1+2) ровняется такой записи
6
-------- это дробь
2(1+2)
2(1+2) можно решить двумя способами -
множить 2 на скобки или решить в скобках, а потом на 2
2х1+2х2=6 2х(1+2=3)=6 ответ одинаковый
6/6
или 6
--
6
как не дели всё равно будет 1.
Поставлю точку что ли. Проблема вытекает из математической неточности при записи деления "в столбик" при использовании горизонтальной черты. Ведь если в примере переписать 6 в числителе, а всё остальное в знаменателе - сомнений ни у кого не возникнет. Ответ будет однозначно 1 и это будет правильный ответ.
Теперь, допустим, перед нами задача запихнуть наш пример в строку. Очевидно что для компутера не существует никаких вертикальных черт. Также допустим что мы не очень внимательны и просто тупо заменяем черту делением, т.е. "/" или "*" в зависимости от парсера. Считаем в любом калькуляторе и с некоторой вероятностью (в зависимости от ответа на вопрос топика разрабочиком калькулятора) получаем 9. И это тоже правильный ответ.
Получаем 2 разных правильных результата для, как мы уверены, идентичного выражения. И проблема собственно в том, выражения в этих случаях нифига не идентичны. Напоминаю про порядок операций: скобки, умножение(то же самое что и деление), сумма. И вот когда мы пишем дробь с вертикальной чертой, на числитель и знаменатель неявно накладываются скобки, а между ними ставится знак деления. И вот про знак деления почему-то все помнят, когда избавляются от черты, а про скобки забывают. Либо намеренно вкладывают в "слеш" смысл вертикальной черты. Но единого стандарта по слешу нет, кто-то интерпретирует его как знак деления, а кто-то как знак деления со скобками для числителя со знаменателем. Проблему ещё создает то, что иногда они взаимозаменяемы, но это не общий случай, о чем многие забывают.
Иными словами:
1) a/b != a:b
2) a/b == (a):(b)
Из чего кстати следует что 2*2+2 != (2)*(2+2).
Чтобы понять почему выражение 6/2(1+2) в одном калькуляторе выдаёт 9, а в другом 1 - надо помнить об одном единственном правиле: для любого вычислительного устройства действие умножения и деления равнозначны (если, конечно, разработчик не заложил какую-то иную логику, что было бы нарушением правил математики?).

Сколько метров дос 1 шаr = 1 метр. Г ДОМАШНЕЕ ЗАДАНИЕ 11 Реши задачу При В урожайный год фермеру удалось собрать 18 ц/га, а в неурожайный - только 8 ц … /га. Какой урожай пшеницы он собирал в каждый из этих годов, если под пшеницу у него отведено 300 га?Можно плиз условия
Равносильные уравнения. Линейное уравнение с одной переменной. Решение линейных уравнений с одной переменной. Урок 2
Большинство современных сабвуферных динамиков оборудованы двумя катушками. Подключение сабвуфера 2 2 осуществляется двумя способами, в зависимости от которых можно получить разное сопротивление. Чем оно меньше, тем большую мощность будет отдавать усилитель.
В этой статье мы расскажем вам о схемах коммутации и объясним, чем отличаются последовательный и параллельный способы, а также поговорим о характеристиках усилителей, так как не все из них могут стабильно работать в низкоомную нагрузку.
Так же советуем ознакомиться со статьей “как подключить усилитель для сабвуфера”, в ней вы найдете схему подключения и рекомендации по подбору силовых и сигнальных проводов.

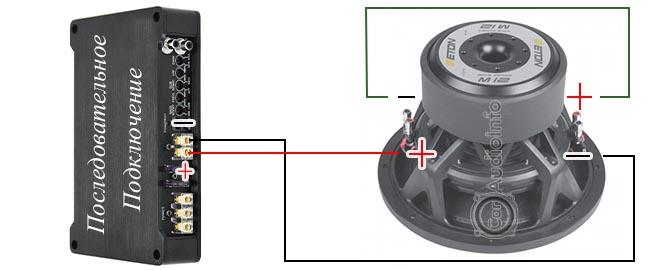
Последовательное и параллельное подключение
Для подключения сабвуферного динамика используют последовательное или параллельное соединение. Если же стоит такая задача, как подключить два сабвуфера и более, может применяться одновременно и последовательное, и параллельное соединение.

Какие усилители в какое сопротивление можно подключать
Понижая сопротивление, мы вынуждаем усилитель отдавать большую мощность. К примеру, при подключении динамика в 4 Ом усилитель будет выдавать 500 Вт, а если этот же динамик переподключить в 1 Ом, мощность составит 1000 Вт.
К минусам низкоомного подключения можно отнести:
- Повышение нагрузки на бортовую сеть автомобиля.
- Увеличение искажения усилителя.
Говоря проще, мы жертвуем качеством звука в пользу громкости. Но не все усилители можно подключать в низкоомную нагрузку. Как правило, производитель указывает в инструкции, при каком сопротивлении усилитель будет стабильно работать, не уходя в защиту и не выходя из строя.
Первое, на что мы обратим внимание, это классы усилителей: AB и D.
- Усилители AB класса имеют очень маленький КПД, то есть из 100% мощности, которая на них поступает, в звук преобразуются только 50-60%, остальное превращается в тепло. Как правило, производители рекомендуют использовать такие усилители в 4 или 2 Ом. Если же такой усилитель подключить в 1 или 0,5 Ом, он будет сильно греться. При наличии защиты, он выключится сам. Если её нет, просто сгорит.
- Усилители D-класса имеют КПД более 80%, в результате чего мало греются. Такие усилители не боятся низкоомной нагрузки. Производитель рекомендует подключать их вплоть до 1 Ом. Но многие подключают такие усилители и к 0,5 Ом – здесь всё зависит от питания и надёжности усилителя.
Кроме того, усилители могут отличаться по количеству каналов. Используя двух – или четырёхканальный усилитель для подключения сабвуфера, вы будете подключать его мостовым соединением. В этом режиме устройство уже работает на свою максимальную нагрузку. Если ваш усилитель, подключённый мостом, AB класса, то его можно использовать в нагрузку только 4 Ом. При подключении в более низкую нагрузку, даже 2 Ом, он будет сильно греться и, возможно, уходить в защиту, или просто сгорит.
Если усилитель, который вы хотите подключить, имеет D-класс, скорее всего, он более пригоден для низкоомной нагрузки, и его можно подключать в 2 Ом. Но сначала стоит всё же уточнить в инструкции, допускает ли это завод-изготовитель.
Предупреждение! Подключить усилитель в более низкое сопротивление (ниже чем указано в инструкции) можно только при соблюдении следующих условий: хорошее питание и не максимальная нагрузка. Но помните, что в этом случае шанс выхода аппаратуры из строя увеличивается в разы. Если что-то пойдёт не так, в гарантии вам будет отказано, так как вы используете устройство вопреки рекомендациям, которые указал производитель.
Схемы коммутации одного сабвуфера к усилителю
В этом разделе мы собрали все возможные варианты сабвуферов и вариации их подключения
Динамик с двумя катушками 4+4 Ома
Как его можно подключить?
- Используя последовательную схему в 8 ом.
- Используя параллельную схему в 2 ома.
Динамик с двумя катушками 2+2 Ома
Как его можно подключить?
Динамик с двумя катушками 1+1 Ома
Как его можно подключить?
Схемы коммутации двух сабвуферов к усилителю
В этом разделе мы собрали “почти” все возможные варианты подключения двух сабвуферов
Два динамика с двумя катушками 4+4 Ома
Как их можно подключить?
Два динамика с двумя катушками 2+2 Ома
Как их можно подключить?
Два динамика с двумя катушками 1+1 Ом
Как их можно подключить?
Видео как подключить сабвуфер с двумя катушками
Заключение
И напоследок, есть желание помочь проекту? Подписывайся на группу “Вконтакте” и “Instagram”. Спасибо, и добро пожаловать в банду 😉

Разные результаты

Если вы уже пытались решить вышеуказанный пример, вы, вероятно, получили два результата: 1 или 9.
Несколько раз в соцсетях распространялись простые арифметические расчеты, которые вызывают споры среди пользователей. Ведь не все приходят к одному и тому же решению. Почему при выполнении одной и той же операции появляются разные результаты?
Ключ к решению
Итак, вы должны начать решать пример справа налево. Сперва выполняются действия в скобках. Затем нужно приступать к умножению и делению. Следом идет сложение и вычитание. Вы должны запомнить этот порядок. Тогда вы сможете решить спорный пример.
Пошаговое решение

Первый шаг – решите то, что находится в скобках. В нашем случае мы имеем (1+2), следовательно, ответ будет 3. Пример теперь будет выглядеть так: 6:2(3).
Дальше приходит сомнение: нужно делить или умножать? Обе операции имеют одинаковый уровень приоритета.
Второй шаг выглядит так. Мы выполняем операцию двумя способами:
- Выполняем умножение: 2 Х 3 = 6. После реализуем последнюю операцию: 6 : 6 = 1.
- Реализуем деление: 6 : 2 = 3. После выполняем умножение: 3 Х 3 = 9.
1 или 9?

Математика не является субъективным вопросом. Каждый знает, что 1 + 1 = 2. Так какой же ответ правильный?
Некоторых учили, что 2(3) равно 2 Х 3, поэтому операция будет выглядеть так: 6 : 2 Х 3. И, если решать справа налево, результат будет 9.
Тем не менее, другие учили, что 2(3) – это то же самое, что (2 Х 3). Так что умножение будет выполнено перед делением. Далее операция будет реализована как 6 : 6, давая в качестве конечного результата 1.
Линклеттер объясняет, что математически противоречиво полагать, что a (b) взаимозаменяемо с axby, а а (b) взаимозаменяемо с (ab) потому, что тогда следует, что 1 = 9.
В подобных случаях эксперты предлагают окончательный ответ. Однако на этот раз кажется маловероятным, что пример решен. Ведь это не чисто математическая проблема, а вопрос коммуникации.
Как упоминалось выше, оба варианта одинаково популярны, поэтому одно из решений не может быть навязано, имея большее количество последователей.
Теперь вы знаете, что можете продолжать защищать свой способ решения этого типа операций. Но если вы говорите, что один из них неверный, то ошибаетесь как раз вы.
Читайте также:



