Как сделать плоскость проецирующей

Рассмотрим решение задач, используя способ замены плоскостей проекций. При этом способе объект сохраняет своё положение в пространстве,а положение плоскостей проекций последовательно меняется. Любые две взаимно перпендикулярные плоскости могут быть приняты за новую систему плоскостей проекций, но при этом понятие горизонтальной и фронтальной плоскостей проекций сохраняется.
Задача №1. Преобразовать комплексный чертеж так, чтобы прямая общего положения АВ оказалась параллельной одной из плоскостей проекций т.е. прямой уровня (горизонталь или фронталь) новой системы (рис. 5.1).
Для решения задачи необходимо заменить плоскость проекций П1, или П2 новой плоскостью проекций П4, параллельной прямой АВ и перпендикулярной к незаменяемой плоскости проекций.
Такая задача решается на комплексном чертеже при необходимости определения натуральной длины отрезка прямой и угла наклона этого отрезка к плоскостям проекций. Для того чтобы прямая АВ в новой системе плоскостей проекций стала, например, фронталью, нужно заменить фронтальную плоскость проекций П2новой плоскостью П4 ⊥ П1 и параллельной прямой АВ.
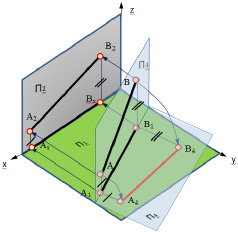
Рис. 5.1. Изображение в пространстве преобразования прямой линии
общего положения в прямую линию уровня
Рассмотрим подробно этапы построения на комплексном чертеже (рис. 5.2), необходимые для решения первой основной задачи на преобразование комплексного чертежа:
1) провести новую ось проекций х14 параллельно А1В1 на произвольном расстоянии от нее; такое положение оси х14 обусловливается тем, что П4 параллельна АВ. В частном случае, если плоскость П4 проведена непосредственно через прямую АВ, ось х14 = А1В1;
2) выбрать на прямой две точки А(А1А2) и В(В1В2);
3) построить проекции точек А и В на плоскости П4.
Прямая А4В4 является проекцией прямой АВ на плоскость П4. Прямая AB в новой системе плоскостей проекций П1/П4 является фронталью.
Отрезок [АВ] прямой проецируется на плоскость П4 в истинную величину, т.е. |А4В4| = |АB|, α°– величина угла наклона прямой АВ к плоскости П1.
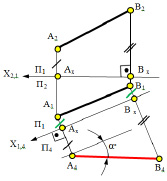
Рис. 5.2. Изображение преобразования прямой линии общего положения
в прямую линию уровня
3адача 2. Преобразовать комплексный чертеж так, чтобы линия общего положения АВ стала проецирующей (рис. 5.3).
Для решения задачи необходимо выполнить две замены плоскостей проекций – заменить фронтальную плоскость проекций П2 исходной системы П2/П1 вспомогательной проецирующей плоскостью П4 || А1В1.При этом плоскость П4 будет перпендикулярной П1 так как АВ || П4 и образует с ней новую систему плоскостей проекций П1/П4.
Построения на комплексном чертеже:
1) провести новую ось проекций х14 || А1В1;
2) построить проекции точек А и В на плоскости П4, взяв координаты точек из плоскости П2;
3) заменить плоскость П1 на новую П5, которая будет ⊥ А4В4. Для этого нужно провести новую ось проекций х4,5.
Так как расстояния точек А и В до плоскости П4 одинаковы, то проекции их на плоскости П5 совпадут, А5 ≡ В5, прямая АВ (А5В5) в новой системе плоскостей проекций займёт проецирующее положение и станет горизонтально проецирующей.
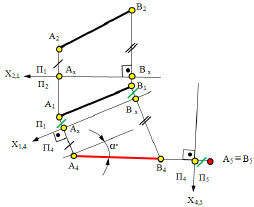
Рис. 5.3. Изображение преобразования прямой линии АВ общего положения
в прямую горизонтально-проецирующую линию.
Задача №3. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала проецирующей (рис. 5.4, 5.5).

Для решения задачи необходимо заменить плоскость П1 или П2исходной системы П2/П1 новой плоскостью П4, перпендикулярной плоскости (АВС).
Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости , преобразовать в проецирующую, то данная плоскость в новой системе плоскостей проекций станет проецирующей. Проще всего для этой цели воспользоваться линией уровня.
На рис. 5.4 плоскость (АВС) общего положения преобразована во фронтально-проецирующую путем преобразования её горизонтали h(h1,h2), во фронтально-проецирующее положение. В новой системе плоскостей проекций П1/П4 плоскость является фронтально проецирующей ( ⊥ П4), и поэтому её проекция на П4 вырождается в прямую линию 4 (С4, А4, В4).

В этом случае α° – величина угла наклона плоскости к плоскости П1.
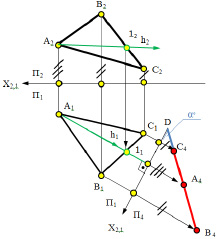
Рис. 5.4. Преобразование плоскости общего положения
в проецирующую плоскость для определения угла наклона α°к П1
Для определения угла наклона (β°), заданной плоскости к фронтальной плоскости проекций (П4), необходимо выполнить преобразования построения, аналогичные преобразованиям, рассмотренным выше (рис.5.5), используя фронталь.
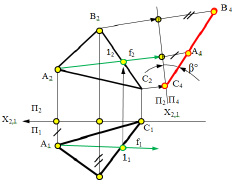
Рис. 5.5. Преобразование плоскости общего положения
в проецирующую плоскость для определения угла наклона β° к П2
В этом случае плоскость преобразуется в горизонтально проецирующую плоскость с помощью её фронтали, которая преобразуется в горизонтально – проецирующую линию.
Задача № 4. Преобразовать комплексный чертеж так, чтобы плоскость общего положения стала плоскостью уровня (параллельной одной из плоскостей проекций) новой системы (рис.5.6).
Плоскость общего положения преобразовать в плоскость уровня заменой только одной плоскости проекций нельзя, так как плоскость П4, параллельная ей, не будет перпендикулярна ни одной из старых плоскостей проекций и, следовательно, не образует ни с одной из них прямоугольной системы плоскостей проекций.
Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить две последовательные замены плоскостей проекций. В начале решения плоскость необходимо преобразовать в проецирующую, т. е. решить задачу 3 на преобразование комплексного чертежа, а затем проецирующую плоскость преобразовать в плоскость уровня.
На рис. 5.6 показан алгоритм преобразования плоскости Δ(АВС) в плоскость уровня.
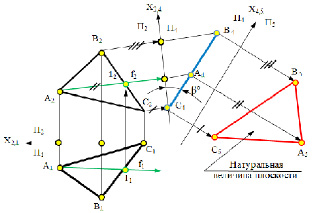
Рис. 5.6. Решение задачи на преобразование плоскости общего положения
в плоскость уровня.
Рассмотрим ещё один возможный вариант (рис. 5.7). Допустим, что необходимо определить натуральную величину фронтально проецирующей плоскости Г(ΔАВС). Для этого заменим плоскость П1 новой плоскостью проекций П4, параллельной плоскости Г(ΔАВС) и, перпендикулярной незаменяемой плоскости П1. В новой системе плоскостей проекций П2/П4 плоскость Г(АВС) станет плоскостью уровня новой плоскости проекций.
Построения на комплексном чертеже:
1) провести новую ось проекций х2,4 параллельно А2С2 на произвольном от нее расстоянии;
2) построить проекции точек А, В и С на плоскость П4;
3) треугольник А4В4С4 является проекцией плоскости треугольника АВС на плоскость П4.
Примечание. Так как плоскость треугольника АВС параллельна П4, значит отображение этого треугольника на П4 величина натуральная. Значит, третья задача на преобразование плоскости уже решена и для решения четвёртой задачи необходимо выполнить одну замену плоскостей проекций. Необходимо горизонтальную плоскость проекций заменить на плоскость П4 и создать новую систему П2 /П4.
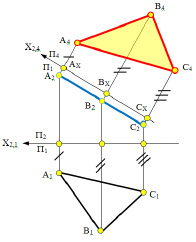
Рис. 5.7. Решение четвертой задачи на преобразование фронтально проецирующей плоскости в плоскость уровня
Иногда недостаточно ввести одну или две дополнительные плоскости проекций, тогда исходную систему плоскостей проекций последовательно дополняют тремя или даже большим числом дополнительных плоскостей.

Рассмотрим случай введения одной дополнительной плоскости. Такой подход применяется для определения натуральной величины отрезка (что равносильно задаче о преобразовании прямой общего положения в прямую частного положения). На рис. 5.4 в системе двух плоскостей проекций щ и щ изображены две проекции отрезка А В прямой общего положения — Л В' и Л" В". Дополнительная плоскость располагается так, чтобы она была параллельна отрезку ЛВ, а новая ось проекций Ахх параллельна горизонтальной проекции отрезка Л'В'. Далее на чертеже производят следующие построения:
О от концов отрезка Л В' восстанавливаются перпендикуляры так, чтобы они пересекали новую ось проекций Ахх;
О на перпендикулярах от новой оси Ахх откладывают расстояния, равные расстояниям от старой оси Ах до т. А" и В", и получают соответственнот. Axw Вх
О соединяют полученные точки и получают отрезок АХВХ, который по длине равен отрезку АВ (решение задачи определения натуральной длины отрезка АВ), а угол ср равен углу наклона отрезка АВ к горизонтальной плоскости проекций щ.
Введя еще одну дополнительную плоскость, можно сделать так, что проекция прямой будет точкой, следовательно, в новой системе плоскостей проекций прямая станет проецирующей.
Введение двух дополнительных плоскостей требуется при решении задачи об определении натуральных размеров треугольника, лежащего в плоскости общего положения (что равносильно преобразованию плоскости общего положения в плоскость частного положения).
Пусть имеется треугольник АВС, принадлежащий плоскости общего положения. Для определения его натуральных размеров вводят две дополнительные плоскости:
О первую дополнительную плоскость вводят таким образом, чтобы в полученной системе плоскостей проекций плоскость треугольника АВС оказалась бы проецирующей; при этом одна из проекций треугольника будет прямой линией;
О вводя еще одну дополнительную плоскость так, чтобы относительно новой системы плоскостей проекций плоскость треугольника была бы плоскостью уровня; при этом одна из проекций становится равной по форме и по размерам исходному треугольнику АВС.

На чертеже построения, соответствующие введению дополнительных плоскостей, проводятся следующим образом (рис. 5.5):
О в исходной системе плоскостей проекций даны две проекции треугольника ЛВС — Л В'С и А" В" С”. Через т. А" проводят горизонталь (линию, параллельную оси Ах) до пересечения с отрезком В"С” и получают т. D";
О по линии связи определяют положение проекции D';
О перпендикулярно отрезку A'D' строят новую ось Ах, при этом координаты вершин треугольника относительно этой оси сохраняются — остаются такими же, как и относительно оси Ах. В результате получают отрезок СВи являющийся проекцией исходного треугольника в полученной после введения дополнительной плоскости системе. Плоскость треугольника АВС (плоскость общего положения) в новой системе плоскостей проекций является фронтально проецирующей;
О вводят вторую дополнительную плоскость, для чего параллельно отрезку С В проводят дополнительную ось проекций Лх2;
О перпендикулярно Лх2 проводят линии связи, на которых откладывают отрезки, равные расстояниям от соответствующих точек до первой дополнительной оси Ах;
О соединяют прямыми построенные точки и получают треугольник А2В2С2, который по форме и размерам равен исходному треугольнику АВС.
Плоскости, перпендикулярные к плоскостям проекции, называют проецирующими.
горизонтально-проецирующая плоскость α⊥H;

фронтально-проецирующая плоскость α⊥V;

профильно-проецирующая плоскость α⊥W;

Проецирующая плоскость имеет одно важное свойство , заключающееся в том, что проекция точек, а следовательно, и любых геометрических фигур, принадлежащих горизонтально проецирующей плоскости, принадлежат горизонтальному следу этой плоскости.
Аналогичное утверждение справедливо и для фронтально проецирующей и для профильно проецирующей плоскостей.
Плоскости, перпендикулярные одной из плоскостей проекций, называются проецирующими.
Горизонтально-проецирующая плоскость δ(δ1)⊥ П1 – плоскость, перпендикулярная горизонтальной плоскости проекций П1 (рис. 35, 36). Горизонтально-проецирующая плоскость задается горизонтальным следом плоскости δ1 , который является геометрическим местом горизонтальных проекций всех точек, принадлежащих данной плоскости.



Рис. 36. Комплексный чертеж горизонтально-проецирующей плоскости δ(δ1):
Углы наклона горизонтально-проецирующей плоскости к П2 и П3 проецируются на горизонтальную плоскость проекций в натуральную величину
Фронтально-проецирующая плоскость γ(γ2)⊥ П2 – плоскость, перпендикулярная фронтальной плоскости проекций П2, задается фронтальным следом плоскости γ2 (рис. 37, 38).



Рис. 38. Комплексный чертеж фронтально-проецирующей плоскости γ(γ2):
Проекции всех линий и точек, лежащих во фронтально-проецирующей плоскости, совпадают с фронтальным следом этой плоскости. Углы наклона фронтально-проецирующей плоскости к П1 и П3 проецируются на фронтальную плоскость проекций в натуральную величину.
Профильно-проецирующая плоскость σ(σ3)⊥ П3 – плоскость, перпендикулярная профильной плоскости проекций П3 , задается профильным следом плоскости σ3 (рис. 39, 40).



Рис. 40. Комплексный чертеж профильно-проецирующей плоскости(σ3):
Читайте также:


