Как сделать пешеходный переход в anylogic
Есть ли какой-то конкретный способ (кроме написания функций самостоятельно) для расчета пройденного расстояния объекта ped в пешеходной библиотеке, что-то вроде метода getDistanceDriven() в библиотеке дорожного движения?
Я почти уверен, что ничего не поделаешь . начни кодить сам :)
Mohammad Hasan N.
Ответы 1

Интересный момент, и, вероятно, я буду использовать его в будущем, но сейчас мне нужны эти данные для конкретного ped , выбранного пользователем, а пока мне нужен способ достичь этого значения в моей модели как для расчетов, так и для отображения. Есть ли какая-нибудь форма этого журнала? P.S. Хотя кажется, что это самокодирование, это намного проще.
Mohammad Hasan N.
вы не можете определить, какие отдельные агенты нужно регистрировать, только какой класс (в свойствах класса). Вы можете достичь значений с помощью обычных операторов SQL, но я не уверен, обновляются ли журналы постоянно на протяжении всей модели или только в конце, вам нужно будет это проверить. Но я согласен: самокодирование могло бы быть намного проще.
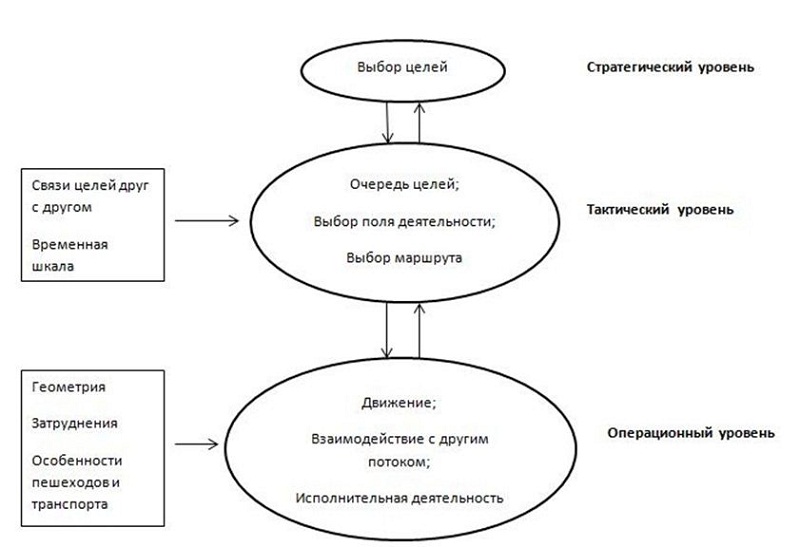
На уровне стратегии пешеход решает, каких целей он хочет добиться и в каком порядке он будет их выполнять. Тактический уровень отвечает за выбор краткосрочных решений – таких как выбор оптимального маршрута в соответствии с особенностями местности, интенсивности движения. Уровень операций описывает непосредственно движение пешехода, т.е. немедленные решения, необходимые, чтобы избежать столкновений и т.п.
Схему принятия решения можно представить в следующем виде:
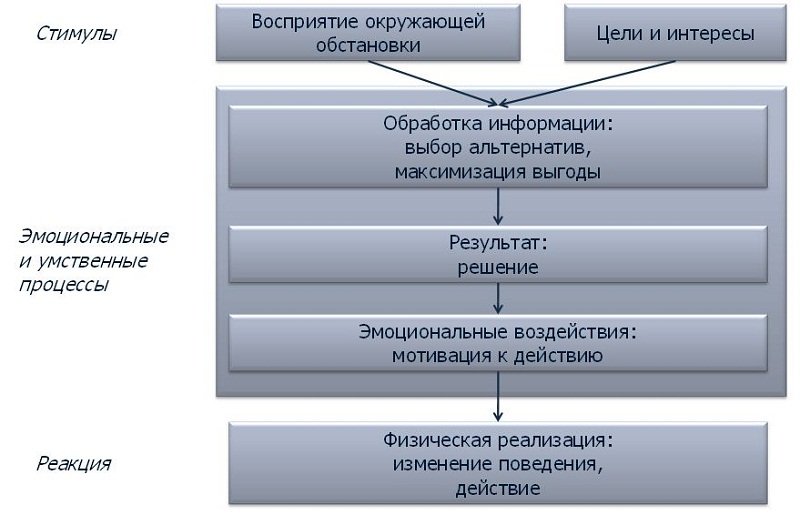
• Выбор микроскопической или макроскопической модели. В представлении микроскопической модели можно выделить некоторое количество пешеходов, определить их характеристики, проследить их маршрут. В макроскопической модели нельзя выделить отдельного пешехода, основополагающими являются пешеходные потоки.
• Дискретная или непрерывная модель.
• Детерминированная или стохастическая модель. В детерминированной модели все возможные реакции определены и неизменны. В стохастической модели пешеход может по-разному реагировать на одну и ту же ситуацию.
Среди существующих моделей пешеходных потоков можно выделить:
• Модель притягивающихся сил: в ней пешеходы представлялись в виде электрических зарядов, находящихся в магнитном поле. Пешеходы и препятствия представляются как положительные заряды, а цели движения как отрицательные заряды;
• Модели, использующие теорию очередей для описания движения пешеходов с использованием вероятностных функций;
• Клеточные автоматы: в них всё пространство представляют собой сетку, в которой каждый пешеход может занимать только одну ячейку. Движение моделируется как перемещение людей между клетками по определенным правилам;
• Газо-кинетическая модель: здесь пешеходы представляются как молекулы в сжиженном газе. Точная скорость и положение пешеходов-молекул неизвестны, вместо этого известно статистическое распределение частиц, исходя из уравнения Больцмана;
• Модель социальных сил: использует Ньютоновскую механику для описания движения пешеходов. Силы порождаются социальными взаимодействиями;
• Расчетные модели: большая часть параметров разово рассчитывается на основании данных практического эксперимента, составляются таблицы зависимости этих параметров от числа пешеходов и размеров помещения. В дальнейшем эти данные используются для описания движения пешеходного потока.
Рассмотрим принципы работы данных моделей более подробно.
1. Модель притягивающихся сил (Magnetic force model)
Достоинства модели:
• Простота реализации;
• Высокая скорость работы модели.
Недостатки модели:
• Невозможность индивидуализации пешехода (определение роста, веса и т.п.);
• Невозможность учета таких явлений как паника, хамство, чрезвычайные ситуации (когда поведение человека становится непредсказуемым);
• Нельзя задать иную линию поведения пешехода, кроме как стремления достичь цели и избежать столкновений с другими пешеходами или препятствиями.
2. Модель обслуживания очередей (Queueing model)
В теории организации очередей движение описано с точки зрения функций плотности вероятности. Пешеходы прибывают с определенной вероятностью в сервер, обслуживаются и встают в очередь. Три главных элемента в системе организации очередей — прибытие, обслуживающий механизм и организация очереди (то есть FIFO). Ласло Ловас предложил стохастическую модель, где пешеходный поток в здании может быть смоделирован как процесс организации сети очередей. В процессе, каждого пешехода рассматривают как единственный объект потока, который взаимодействует с другими объектами. Узлы в созданной сети очередей представляют собой комнаты, а связи рассматриваются как двери. В процессе движения человек выбирает новый узел согласно определенной вероятности, приводящей к новому уравнению, которое описывает изменение в количестве пешеходов со времени t к наступлению момента t+h. Из полученного уравнения можно оценить эффективность эвакуации людей из помещения (то есть ожидаемое оставшееся число людей в узле и ожидаемое число эвакуировавшихся людей).
3. Клеточные автоматы (Cellular automata model)

Клеточные автоматы являются простым и быстрым способом моделирования пешеходного потока. В клеточной модели автоматов всё пространство представляет собой сетку.
Каждая клетка сетки может быть занята одним единственным пешеходом. Движение смоделировано как изменение клеток, где несколько правил применены к автоматам (пешеходам). Эти наборы правил отличаются в различных реализациях данной модели. Некоторые реализации модели будут обсуждены далее.
Блю и Адлер выделили два элемента пешеходного движения: движение вперед и разрешение конфликтов. Движение вперед указывает на желание пешехода достигнуть определенной цели и сводится к определению скорости и ускорения каждого пешехода. Разрешение конфликтов означает желание избежать физического контакта.
Набор правил, предложенных Блю и Адлером, состоит из шести правил, которые применяются на четырех различных этапах. Первый этап применяет правила изменения маршрута. На втором этапе всем пешеходам назначается новая клетка. На третьем этапе правила продвижения применяются для каждого пешехода. На последнем этапе пешеходы скачкообразно перемещаются в новые клетки.
Изменение маршрута в этой модели регулируется пятью правилами. Изменение возможно, только если смежная клетка доступна и не занята пешеходом.
1. Определите, доступны ли клетки непосредственно справа и слева
2. Решение противоречиво, если смежная клетка доступна, но на эту клетку претендует два маршрута. На этом этапе рандомно определяют, какой пешеход получит доступ к клетке.
3. Завершите изменение маршрута, если обе смежных клетки недоступны.
4. Вычислите незанятое расстояние для активных и незанятых смежных маршрутов. Если расстояние уникально и максимально, присвойте пешехода этому маршруту. Это значит, что пешеход выберет путь, у которого нет никаких противоречий на максимально большом участке. Если никакое уникальное максимальное расстояние не найдено, присвойте маршрут согласно правилу пять.
5. Если три маршрута приводят к максимальному расстоянию, применяют разделение 80/10/10 для текущего маршрута и двух смежных маршрутов. Если два маршрута приводят к максимальному расстоянию, применяют разделение 50/50.
После определения маршрута пешеход перемещается по присвоенному ему маршруту. Это осуществляется на втором этапе. На третьем этапе пешеходам присваивается скорость перемещения. Во время этого этапа пешеходы могут поменяться местами с определенной вероятностью. Это может произойти, если два пешехода движутся друг на друга. На этапе четыре все пешеходы перемещаются.
Модель была применена к однонаправленным пешеходным аллеям и двунаправленному потоку, в котором число двигающихся в одном направлении пешеходов много больше пешеходов, двигающихся в обратном направлении.
Дейкстра, Йессурун и Тиммерманс предложили модель с фокусом на перемещение пешеходов в аллее. Во время перемещения пешехода выделены четыре шага:
1. Проверьте, передал ли пешеход решение (конец действия или узел базовой сети). Если это — истина, переходите к шагу три. В противном случае переходите на шаг два.
2. Если пешеход находится в ячейке решения (узел сети), исследуйте поведение пешехода и поверните пешехода в требуемом направлении. Таким образом, решение будет принято.
3. Если новая выбранная ячейка пуста, переместите пешехода в ячейку. В противном случае переходите к шагу четыре.
4. Если ячейка слева или справа не занята, переместитесь налево или направо.
В этой модели перемещение направлено к цели и изменено только в моментах принятия решения. Взаимодействие с другими пешеходами не рассматривалось.
Янг Лижонг и др. разработали модель клеточных автоматов для пожарной эвакуации. Они представили специальные правила для расчета маршрута при пожаре (степень опасности). Эта степень опасности состоит из степени опасности позиции (определенной расстоянием до самого близкого выхода) и степени опасности возгорания (определенной расстоянием до огня). В их модели определены три этапа.
1. Каждый пешеход выбирает ячейку с самой маленькой степенью опасности, относительно его собственного представления. Если все смежные ячейки — заняты или имеют более высокую степень опасности, житель не перемещается.
2. Если больше чем один житель хочет переместиться в ту же самую ячейку, один из желающих выбирается случайным образом. Остальные на этом этапе должны ожидать.
3. Каждый житель обновляет степень опасности.
4. Газокинетическая модель (Gas-kinetic model)
5. Модель социальных сил (Social force model)
Модель социальных сил была разработана Хелбингом и Молнаром. В этой модели различные побуждения и влияния пешехода описаны различными видами силы. Эта модель основывается, главным образом, на Ньютоновской динамике, но масса равна 1. Это приводит к модулю для сил. Эта модель в состоянии воссоздать несколько природных явлений, которые происходят во время пешеходного перемещения:
1. Пешеходы обычно выбирают самый быстрый маршрут;
2. Пешеходы перемещаются с индивидуальной скоростью, принимая во внимание ситуацию, пол, возраст, окружающую среду, и т.д. Скорость представляет собой Гауссово распределение.
Рассмотрим силы и параметры, используемые в данной модели (приведу описание без математического аппарата, т.к. статья все же больше обзорная):
1) Самая очевидная сила — так называемая движущая сила, которая отражает побуждение пешехода, чтобы переместиться к цели с требуемой скоростью.
2) Самое важное взаимодействие между пешеходами — стремление сохранить определенное расстояние до других пешеходов. Чтобы описать это поведение, в модели социальных сил реализовано отталкивание. Отталкивание — зависимо от расстояния между пешеходами — оно имеет самое высокое значение на близком расстоянии (но не вне максимального предела) и стремится к нулю с увеличением расстояния между пешеходами. Это может быть реализовано, с использованием показательной функции, приводя к силе, описывающей взаимодействия между пешеходами.
3) Обычно пешеходное перемещение является анизотропным. Это означает, что действия перед пешеходом более важны чем действия, происходящие позади него. У людей есть возможность предвидеть действия других людей, и таким образом они могут реагировать на действия, предпринятые другими людьми. Чтобы реализовать это в модели социальных сил, действия, происходящие в поле зрения пешехода, должны иметь большую степень влияния, чем действия пешеходов производимые все поля зрения. Чтобы описать подобное поведение, форм-фактор поля зрения реализован так, что он зависит от угла между требуемым направлением перемещения и направлением пешехода, проявляющего отталкивающую силу.

Если лямбда меньше 1, то пешеходное движение может рассматриваться как анизотропное — пешеходы будут неодинаково реагировать на объекты. Объекты впереди оказывают большее влияние на поведение, чем боковые или находящиеся позади пешехода.
4) Сила трения скольжения является результатом того, что пешеходы пытаются избежать столкновения с другими пешеходами, которые движутся с высокой скоростью на маленьких расстояниях.
5) Аттракторы могут влиять на поведение пешеходов. Окна или специальные аттракторы например могут привлечь пешехода, и он переместится к аттрактору, а некоторые (пожар, предупредительная табличка) — отпугнуть. Привлекательность аттрактора зависима от времени и линейно уменьшается к нулю. Аттракторы могут быть смоделированы таким же образом, как и социальная сила между пешеходами
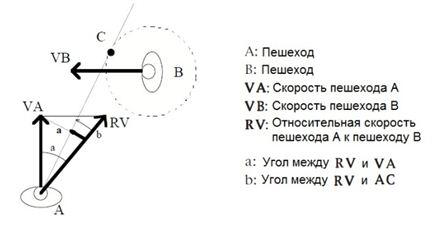
6) Пешеходы часто ходят в группах. После того, как они разделяются (например, если пешеходы должен избежать столкновения с препятствием), отдельные пешеходы пытаются снова преобразовать группу. Это осуществляется под воздействием силы притяжения, действующей от пешехода А к пешеходу Б.
7) Всем пешеходам присуще индивидуальное поведение, и таким образом их перемещение может отличаться от принятых законов. Это поведение представлено колебанием. Колебания нормально распределены и перпендикулярны вектору, указывающему на требуемое направление.
Модель социальных сил состоит из большого количества сил, которые представляют различные влияния, воздействующие на пешехода в реальности. Сумма всех сил описывает перемещение и направление пешехода.
В зависимости от моделируемого случая все силы не обязательно должны рассматриваться (например, физической силой можно пренебречь, если никакой процесс паники или эвакуации не моделируется).
К слову, именно модель социальных сил используется для моделирования пешеходных потоков в PTV VISION VISSIM.
6. Расчетные модели
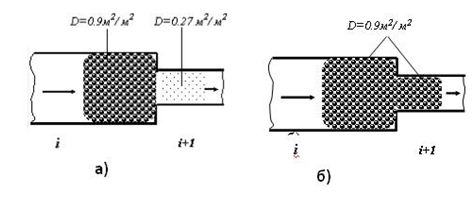
Где а) реальное разуплотнение пешеходного потока, а б) по ГОСТ 12.1.004-91.
На этом я бы хотел закончить данную статью. Данная тематика достаточно большая и интересная, а математики я не касался в ней сознательно. Статья распухла бы, как минимум, в полтора раза, а для вводной статьи и текущая версия вышла достаточно объемной. На данный момент, публикаций на русском языке, посвященных данной теме практически нет, и если моя статья пробудит интерес — то я буду этому только рад.
Есть ли какой-то конкретный способ (кроме написания функций самостоятельно) для расчета пройденного расстояния объекта ped в пешеходной библиотеке, что-то вроде метода getDistanceDriven() в библиотеке дорожного движения?
Я почти уверен, что ничего не поделаешь . начни кодить сам :)
Mohammad Hasan N.
Ответы 1

Интересный момент, и, вероятно, я буду использовать его в будущем, но сейчас мне нужны эти данные для конкретного ped , выбранного пользователем, а пока мне нужен способ достичь этого значения в моей модели как для расчетов, так и для отображения. Есть ли какая-нибудь форма этого журнала? P.S. Хотя кажется, что это самокодирование, это намного проще.
Mohammad Hasan N.
вы не можете определить, какие отдельные агенты нужно регистрировать, только какой класс (в свойствах класса). Вы можете достичь значений с помощью обычных операторов SQL, но я не уверен, обновляются ли журналы постоянно на протяжении всей модели или только в конце, вам нужно будет это проверить. Но я согласен: самокодирование могло бы быть намного проще.

На уровне стратегии пешеход решает, каких целей он хочет добиться и в каком порядке он будет их выполнять. Тактический уровень отвечает за выбор краткосрочных решений – таких как выбор оптимального маршрута в соответствии с особенностями местности, интенсивности движения. Уровень операций описывает непосредственно движение пешехода, т.е. немедленные решения, необходимые, чтобы избежать столкновений и т.п.
Схему принятия решения можно представить в следующем виде:

• Выбор микроскопической или макроскопической модели. В представлении микроскопической модели можно выделить некоторое количество пешеходов, определить их характеристики, проследить их маршрут. В макроскопической модели нельзя выделить отдельного пешехода, основополагающими являются пешеходные потоки.
• Дискретная или непрерывная модель.
• Детерминированная или стохастическая модель. В детерминированной модели все возможные реакции определены и неизменны. В стохастической модели пешеход может по-разному реагировать на одну и ту же ситуацию.
Среди существующих моделей пешеходных потоков можно выделить:
• Модель притягивающихся сил: в ней пешеходы представлялись в виде электрических зарядов, находящихся в магнитном поле. Пешеходы и препятствия представляются как положительные заряды, а цели движения как отрицательные заряды;
• Модели, использующие теорию очередей для описания движения пешеходов с использованием вероятностных функций;
• Клеточные автоматы: в них всё пространство представляют собой сетку, в которой каждый пешеход может занимать только одну ячейку. Движение моделируется как перемещение людей между клетками по определенным правилам;
• Газо-кинетическая модель: здесь пешеходы представляются как молекулы в сжиженном газе. Точная скорость и положение пешеходов-молекул неизвестны, вместо этого известно статистическое распределение частиц, исходя из уравнения Больцмана;
• Модель социальных сил: использует Ньютоновскую механику для описания движения пешеходов. Силы порождаются социальными взаимодействиями;
• Расчетные модели: большая часть параметров разово рассчитывается на основании данных практического эксперимента, составляются таблицы зависимости этих параметров от числа пешеходов и размеров помещения. В дальнейшем эти данные используются для описания движения пешеходного потока.
Рассмотрим принципы работы данных моделей более подробно.
1. Модель притягивающихся сил (Magnetic force model)

Достоинства модели:
• Простота реализации;
• Высокая скорость работы модели.
Недостатки модели:
• Невозможность индивидуализации пешехода (определение роста, веса и т.п.);
• Невозможность учета таких явлений как паника, хамство, чрезвычайные ситуации (когда поведение человека становится непредсказуемым);
• Нельзя задать иную линию поведения пешехода, кроме как стремления достичь цели и избежать столкновений с другими пешеходами или препятствиями.
2. Модель обслуживания очередей (Queueing model)
В теории организации очередей движение описано с точки зрения функций плотности вероятности. Пешеходы прибывают с определенной вероятностью в сервер, обслуживаются и встают в очередь. Три главных элемента в системе организации очередей — прибытие, обслуживающий механизм и организация очереди (то есть FIFO). Ласло Ловас предложил стохастическую модель, где пешеходный поток в здании может быть смоделирован как процесс организации сети очередей. В процессе, каждого пешехода рассматривают как единственный объект потока, который взаимодействует с другими объектами. Узлы в созданной сети очередей представляют собой комнаты, а связи рассматриваются как двери. В процессе движения человек выбирает новый узел согласно определенной вероятности, приводящей к новому уравнению, которое описывает изменение в количестве пешеходов со времени t к наступлению момента t+h. Из полученного уравнения можно оценить эффективность эвакуации людей из помещения (то есть ожидаемое оставшееся число людей в узле и ожидаемое число эвакуировавшихся людей).
3. Клеточные автоматы (Cellular automata model)

Клеточные автоматы являются простым и быстрым способом моделирования пешеходного потока. В клеточной модели автоматов всё пространство представляет собой сетку.
Каждая клетка сетки может быть занята одним единственным пешеходом. Движение смоделировано как изменение клеток, где несколько правил применены к автоматам (пешеходам). Эти наборы правил отличаются в различных реализациях данной модели. Некоторые реализации модели будут обсуждены далее.
Блю и Адлер выделили два элемента пешеходного движения: движение вперед и разрешение конфликтов. Движение вперед указывает на желание пешехода достигнуть определенной цели и сводится к определению скорости и ускорения каждого пешехода. Разрешение конфликтов означает желание избежать физического контакта.
Набор правил, предложенных Блю и Адлером, состоит из шести правил, которые применяются на четырех различных этапах. Первый этап применяет правила изменения маршрута. На втором этапе всем пешеходам назначается новая клетка. На третьем этапе правила продвижения применяются для каждого пешехода. На последнем этапе пешеходы скачкообразно перемещаются в новые клетки.
Изменение маршрута в этой модели регулируется пятью правилами. Изменение возможно, только если смежная клетка доступна и не занята пешеходом.
1. Определите, доступны ли клетки непосредственно справа и слева
2. Решение противоречиво, если смежная клетка доступна, но на эту клетку претендует два маршрута. На этом этапе рандомно определяют, какой пешеход получит доступ к клетке.
3. Завершите изменение маршрута, если обе смежных клетки недоступны.
4. Вычислите незанятое расстояние для активных и незанятых смежных маршрутов. Если расстояние уникально и максимально, присвойте пешехода этому маршруту. Это значит, что пешеход выберет путь, у которого нет никаких противоречий на максимально большом участке. Если никакое уникальное максимальное расстояние не найдено, присвойте маршрут согласно правилу пять.
5. Если три маршрута приводят к максимальному расстоянию, применяют разделение 80/10/10 для текущего маршрута и двух смежных маршрутов. Если два маршрута приводят к максимальному расстоянию, применяют разделение 50/50.
После определения маршрута пешеход перемещается по присвоенному ему маршруту. Это осуществляется на втором этапе. На третьем этапе пешеходам присваивается скорость перемещения. Во время этого этапа пешеходы могут поменяться местами с определенной вероятностью. Это может произойти, если два пешехода движутся друг на друга. На этапе четыре все пешеходы перемещаются.
Модель была применена к однонаправленным пешеходным аллеям и двунаправленному потоку, в котором число двигающихся в одном направлении пешеходов много больше пешеходов, двигающихся в обратном направлении.
Дейкстра, Йессурун и Тиммерманс предложили модель с фокусом на перемещение пешеходов в аллее. Во время перемещения пешехода выделены четыре шага:
1. Проверьте, передал ли пешеход решение (конец действия или узел базовой сети). Если это — истина, переходите к шагу три. В противном случае переходите на шаг два.
2. Если пешеход находится в ячейке решения (узел сети), исследуйте поведение пешехода и поверните пешехода в требуемом направлении. Таким образом, решение будет принято.
3. Если новая выбранная ячейка пуста, переместите пешехода в ячейку. В противном случае переходите к шагу четыре.
4. Если ячейка слева или справа не занята, переместитесь налево или направо.
В этой модели перемещение направлено к цели и изменено только в моментах принятия решения. Взаимодействие с другими пешеходами не рассматривалось.
Янг Лижонг и др. разработали модель клеточных автоматов для пожарной эвакуации. Они представили специальные правила для расчета маршрута при пожаре (степень опасности). Эта степень опасности состоит из степени опасности позиции (определенной расстоянием до самого близкого выхода) и степени опасности возгорания (определенной расстоянием до огня). В их модели определены три этапа.
1. Каждый пешеход выбирает ячейку с самой маленькой степенью опасности, относительно его собственного представления. Если все смежные ячейки — заняты или имеют более высокую степень опасности, житель не перемещается.
2. Если больше чем один житель хочет переместиться в ту же самую ячейку, один из желающих выбирается случайным образом. Остальные на этом этапе должны ожидать.
3. Каждый житель обновляет степень опасности.
4. Газокинетическая модель (Gas-kinetic model)
5. Модель социальных сил (Social force model)
Модель социальных сил была разработана Хелбингом и Молнаром. В этой модели различные побуждения и влияния пешехода описаны различными видами силы. Эта модель основывается, главным образом, на Ньютоновской динамике, но масса равна 1. Это приводит к модулю для сил. Эта модель в состоянии воссоздать несколько природных явлений, которые происходят во время пешеходного перемещения:
1. Пешеходы обычно выбирают самый быстрый маршрут;
2. Пешеходы перемещаются с индивидуальной скоростью, принимая во внимание ситуацию, пол, возраст, окружающую среду, и т.д. Скорость представляет собой Гауссово распределение.
Рассмотрим силы и параметры, используемые в данной модели (приведу описание без математического аппарата, т.к. статья все же больше обзорная):
1) Самая очевидная сила — так называемая движущая сила, которая отражает побуждение пешехода, чтобы переместиться к цели с требуемой скоростью.
2) Самое важное взаимодействие между пешеходами — стремление сохранить определенное расстояние до других пешеходов. Чтобы описать это поведение, в модели социальных сил реализовано отталкивание. Отталкивание — зависимо от расстояния между пешеходами — оно имеет самое высокое значение на близком расстоянии (но не вне максимального предела) и стремится к нулю с увеличением расстояния между пешеходами. Это может быть реализовано, с использованием показательной функции, приводя к силе, описывающей взаимодействия между пешеходами.
3) Обычно пешеходное перемещение является анизотропным. Это означает, что действия перед пешеходом более важны чем действия, происходящие позади него. У людей есть возможность предвидеть действия других людей, и таким образом они могут реагировать на действия, предпринятые другими людьми. Чтобы реализовать это в модели социальных сил, действия, происходящие в поле зрения пешехода, должны иметь большую степень влияния, чем действия пешеходов производимые все поля зрения. Чтобы описать подобное поведение, форм-фактор поля зрения реализован так, что он зависит от угла между требуемым направлением перемещения и направлением пешехода, проявляющего отталкивающую силу.

Если лямбда меньше 1, то пешеходное движение может рассматриваться как анизотропное — пешеходы будут неодинаково реагировать на объекты. Объекты впереди оказывают большее влияние на поведение, чем боковые или находящиеся позади пешехода.
4) Сила трения скольжения является результатом того, что пешеходы пытаются избежать столкновения с другими пешеходами, которые движутся с высокой скоростью на маленьких расстояниях.
5) Аттракторы могут влиять на поведение пешеходов. Окна или специальные аттракторы например могут привлечь пешехода, и он переместится к аттрактору, а некоторые (пожар, предупредительная табличка) — отпугнуть. Привлекательность аттрактора зависима от времени и линейно уменьшается к нулю. Аттракторы могут быть смоделированы таким же образом, как и социальная сила между пешеходами
6) Пешеходы часто ходят в группах. После того, как они разделяются (например, если пешеходы должен избежать столкновения с препятствием), отдельные пешеходы пытаются снова преобразовать группу. Это осуществляется под воздействием силы притяжения, действующей от пешехода А к пешеходу Б.
7) Всем пешеходам присуще индивидуальное поведение, и таким образом их перемещение может отличаться от принятых законов. Это поведение представлено колебанием. Колебания нормально распределены и перпендикулярны вектору, указывающему на требуемое направление.
Модель социальных сил состоит из большого количества сил, которые представляют различные влияния, воздействующие на пешехода в реальности. Сумма всех сил описывает перемещение и направление пешехода.
В зависимости от моделируемого случая все силы не обязательно должны рассматриваться (например, физической силой можно пренебречь, если никакой процесс паники или эвакуации не моделируется).
К слову, именно модель социальных сил используется для моделирования пешеходных потоков в PTV VISION VISSIM.
6. Расчетные модели

Где а) реальное разуплотнение пешеходного потока, а б) по ГОСТ 12.1.004-91.
На этом я бы хотел закончить данную статью. Данная тематика достаточно большая и интересная, а математики я не касался в ней сознательно. Статья распухла бы, как минимум, в полтора раза, а для вводной статьи и текущая версия вышла достаточно объемной. На данный момент, публикаций на русском языке, посвященных данной теме практически нет, и если моя статья пробудит интерес — то я буду этому только рад.
Читайте также:


