Как сделать перпендикулярные прямые
2) \u043e\u0442\u043c\u0435\u0447\u0430\u0435\u043c \u043d\u0430 \u043d\u0435\u0439 \u043f\u0440\u043e\u0438\u0437\u0432\u043e\u043b\u044c\u043d\u043e \u0442\u043e\u0447\u043a\u0438 \u0410 \u0438\u0412
3) \u0441 \u043f\u043e\u043c\u043e\u0449\u044c\u044e \u0446\u0438\u0440\u043a\u0443\u043b\u044f \u043f\u0440\u043e\u0432\u043e\u0434\u0438\u043c \u0434\u0432\u0435 \u043e\u043a\u0440\u0443\u0436\u043d\u043e\u0441\u0442\u0438 \u0441 \u0446\u0435\u043d\u0442\u0440\u0430\u043c\u0438 \u0432 \u0442\u043e\u0447\u043a\u0430\u0445 \u0410 \u0438 \u0412 \u0440\u0430\u0434\u0438\u0443\u0441\u043e\u043c \u0431\u043e\u043b\u044c\u0448\u0435 \u043f\u043e\u043b\u043e\u0432\u0438\u043d\u044b \u043e\u0442\u0440\u0435\u0437\u043a\u0430 \u0410\u0412
4) \u0441\u043e\u0435\u0434\u0438\u043d\u044f\u0435\u043c \u0442\u043e\u0447\u043a\u0438 \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0435\u043d\u0438\u044f \u043e\u043a\u0440\u0443\u0436\u043d\u043e\u0441\u0442\u0435\u0439 \u0441 \u043f\u043e\u043c\u043e\u0449\u044c\u044e \u043b\u0438\u043d\u0435\u0439\u043a\u0438 - \u044d\u0442\u043e \u0438 \u0435\u0441\u0442\u044c \u043f\u0440\u044f\u043c\u0430\u044f \u043f\u0435\u0440\u043f\u0435\u043d\u0434\u0438\u043a\u0443\u043b\u044f\u0440\u043d\u0430\u044f \u043f\u0440\u044f\u043c\u043e\u0439 \u0410\u0412">]" data-testid="answer_box_list">

1) с помощью линейки чертим прямую
2) отмечаем на ней произвольно точки А иВ
3) с помощью циркуля проводим две окружности с центрами в точках А и В радиусом больше половины отрезка АВ
4) соединяем точки пересечения окружностей с помощью линейки - это и есть прямая перпендикулярная прямой АВ

Новые вопросы в Геометрия
Средняя линия равнобедренного треугольника, параллельная боковой стороне, равна 9. Найдите пожалуйста длину основания этого треугольника, если его пер … иметр равен 60. Объяснение не обязательно, но было бы полезным.
Скільки можна утворити пар вертикальних кутiв, що мають можна провести? спільну вершину в заданій точці?
Перпендикулярные прямые.
Пусть а и b — прямые, пересекающиеся в точке А (рис. 1). Каждая из этих прямых точкой А делится на две полупрямые. Полупрямые одной прямой образуют с полупрямыми другой прямой четыре угла. Пусть альфа — один из этих углов. Тогда любой из остальных трех углов будет либо смежным с углом альфа, либо вертикальным с углом альфа.
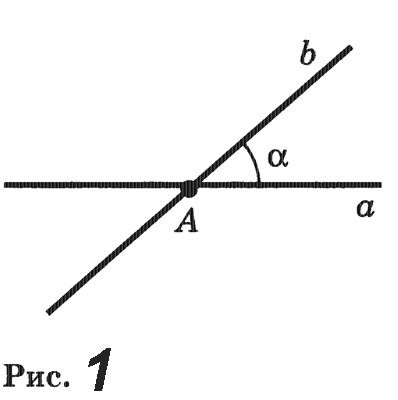
Отсюда следует, что если один из углов прямой, то остальные углы тоже будут прямые, В этом случае мы говорим, что прямые пересекаются под прямым углом.
Определение.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом (рис. 2).
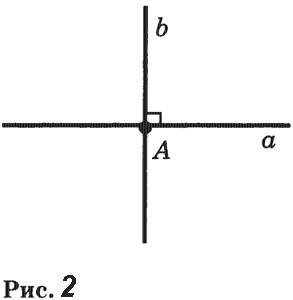
Перпендикулярность прямых обозначается знаком ⊥ Запись а ⊥ b читается: Прямая а перпендикулярна прямой b.
Теорема.
Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Доказательство.
Пусть а — данная прямая и А — данная точка на ней. Обозначим через ах одну из полупрямых прямой а с начальной точкой А (рис. 3). Отложим от полупрямой а1 угол (a1b1), равный 90°.
Тогда прямая, содержащая луч b1, будет перпендикулярна прямой а.
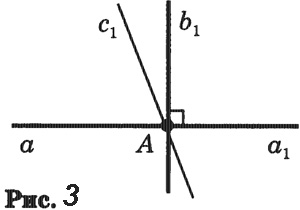
Допустим, что существует другая прямая, проходящая через точку А и перпендикулярная прямой а. Обозначим через с1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b2. Углы (a1b1) и (a1c1), равные каждый 90°, отложены в одну полуплоскость от полупрямой а1. Но от полупрямой а1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не может быть другой прямой, проходящей через точку А и перпендикулярной прямой а. Теорема доказана.
Определение.
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
На рисунке 4 перпендикуляр АВ проведен из точки А к прямой а. Точка В — основание перпендикуляра.
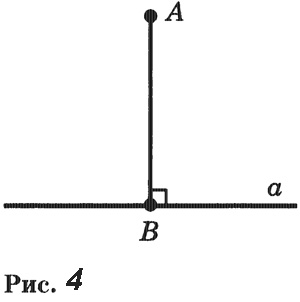
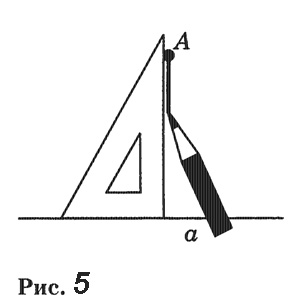
Для построения перпендикуляра пользуются чертежным угольником (рис. 5).
Построение прямых углов на местности
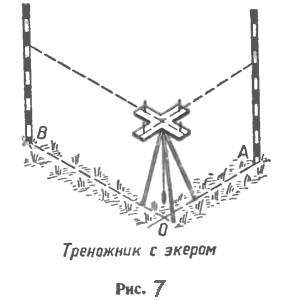
Для построения прямых углов на местности применяют специальные приборы, простейшим из которых является экер. Экер представляет собой два бруска, расположенных под прямым углом и укрепленных на треножнике (рис. 7). На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны. Чтобы построить на местности прямой угол с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (прямая ОВ на рисунке 7). Получается прямой угол АОВ.
В геодезии для построения прямых углов используются более совершенные приборы, например теодолит.
По горизонтали:
3. Отрезок прямой, соединяющий точку окружности с ее центром. 6. Утверждение, не требующее доказательства. 9. Конструкция, система мысли. 10. Вид четырехугольника. 15. Отрезок прямой, соединяющий две точки кривой. 16. Мера длины. 17. Тригонометрическая функция. 18. Точка пересечения диаметров окружности. 19. Тригонометрическая функция. 20. Часть окружности. 21. Старинная мера длины.
По вертикали:
1. Символ какого-либо алфавита. 2. Вид параллелограмма. 4. Хорда, проходящая через центр окружности. 5. Геометрический элемент. 7. Луч, делящий угол пополам. 8. Символ греческого алфавита. 10. Сумма длин сторон треугольника. 11. Вспомогательное предложение, используемое для доказательства. 12. Элемент прямоугольного треугольника. 13. Одна из замечательных линий треугольника. 14. Тригонометрическая функция.
Интересная задача
Есть такая задача:
В Заколдованном Лесу било 10 заколдованных источников - номер 1, 2, 3. 10. Вода каждого источника была неотличима на цвет, вкус и запах от обычной воды, но являлась сильнейшим ядом. Выпивший её был обречён - если только в течение часа после этого не пил воды источника с бОльшим номером (например, от яда источника 3 спасали источники 4-10; яд 10-го источника не оставлял шансов на спсасение). Первые 9 источников были общедоступны, но источник 10 был в пещере Кащея Бессмертного, и доступ к нему имел только Кащей.
И вот однажды Иван-Дурак вызвал Кащея на поединок. Условия были простыми: каждый приносит с собой по стакану некоторой жидкости, соперники обмениваются стаканами и выпивают их содержимое. А дальше - справляются, как могут.
Кащей был доволен. Ещё бы: он даст Ивану яд номер 10, и Ивана ничто не сможет спасти. А сам он яд, данный Иваном, запьёт водой 10-го источника - и будет спасён.
Попробуйте разработать план дуэли для Ивана. Задача - остаться жить самому и прикончить Кащея.
Ответ 1. Угробить Кащея. Ему нужно дать не яд, а чистую воду. Он запьёт её своим ядом - и он обречён.
Ответ 2. Не угробиться самому. Любой яд, кроме номера 1, может являться и противоядием. Перед тем, как придти на дуэль, нужно выпить яд малого номера. И тогда яд номер 10, полученный от Кащея на дуэли, не убьёт, а спасёт.
Вообще, идея-то тривиальная. Не всегда можно взвесить поступок изолированно. Одно и то же действие может оказаться и ядом, и противоядием. Многое зависит от фона. Не буду говорить, что всё - но, несомненно, многое.
И когда вы слышите, что кто-то из ваших знакомых совершил Такую-То и Такую-То Гадости, не спешите вешать ярлыки. Уверены ли вы, что это именно гадости? Не может ли быть, что они просто выглядят так? Уверены ли вы, что фон этих действий вам известен?
Построение перпендикулярной прямой
Сейчас мы с вами с помощью циркуля попробуем построить перпендикулярную прямую. Для этого у нас есть точка О и прямая а.
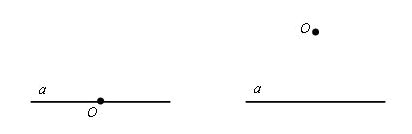
На первом рисунке изображена прямая на которой лежит точка О, а на втором данная точка не лежит на прямой а.
Теперь давайте по отдельности рассмотрим эти оба варианта.
1-й вариант
Вначале мы берем циркуль, ставим его в центр точки О и чертим окружность с произвольным радиусом. Теперь мы видим, что данная окружность пересекает прямую а в двух точках. Пускай это будут точки А и В.
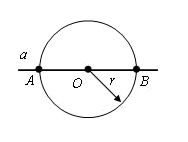
Далее, мы берем и проводим окружности из точек А и В. Радиус этих окружностей будет АВ, а вот точка С будет точкой пересечения этих окружностей. Если вы помните, то в самом начале мы с вами получили точки А и В, когда чертили окружность и брали произвольный радиус.
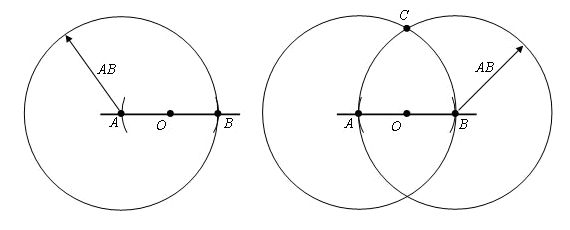
В итоге мы видим, что искомая перпендикулярная прямая проходит через точки С и О.
Доказательство
Для данного доказательства нас нужно провести отрезки AC и CB. И мы видим, что образовавшиеся треугольники равны: Δ ACO = Δ BCO, это следует из третьего признака равенства треугольников, то есть у нас выходит, что AO = OB, AC = CB, а СО общая по построению. Образовавшиеся углы ∠ COA и ∠ COB равны и оба имеют величину, равную 90 °. Из этого следует, что прямая CO перпендикулярна AB.
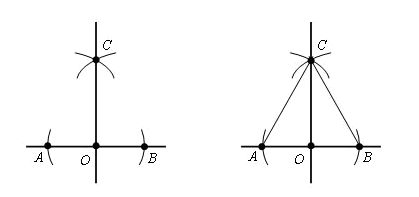
Отсюда мы можем сделать вывод, что углы, образованные при пересечении двух прямых являются перпендикулярными в том случае, если хотя бы один из них перпендикулярен, а это значит, что такой угол равен 90 градусам и является прямым.
2-й вариант
А сейчас давайте рассмотрим вариант построения перпендикулярной прямой, где данная точка не лежит на прямой а.
В этом случае мы с помощью циркуля из точки О проводим окружность с таким радиусом, чтобы эта окружность пересекала прямую а. А точки А и В пускай будут точками пересечения этой окружности с данной прямой а.
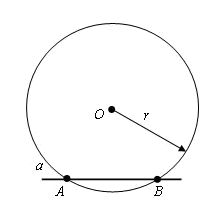
Далее, мы берем такой же радиус, но проводим окружности, центром которых будут точки A и B. Смотрим на рисунок и видим, что у нас появилась точка О1, которая также является точкой пересечения окружностей и лежит в полуплоскости, но отличной от той, в которой находится точка О.
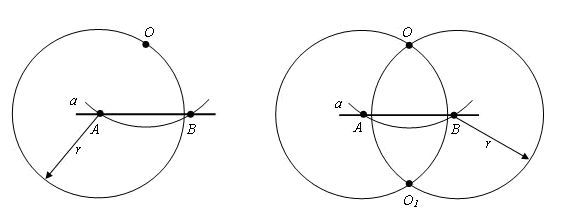
Следующее, что мы сделаем, так это через точки O и O1проведем прямую. Это и будет та перпендикулярная прямая, которую мы искали.
Доказательство
Припустим, что точкой пересечения прямых OO1 и AB является точка С. Тогда треугольники AOB и BO1A равны по третьему признаку равенства треугольников и AO = OB = AO1 = O1B, а АВ является общей по построению. Из этого следует, что углы OAС и O1AC равны. Треугольники OAC и O1AC, следуя из первого признака равенства треугольников AO равняется AO1, а по построению, углы OAС и O1AC равны при общей AС. Следовательно, что угол OСA равен углу O1CA, но а так как они смежные, то значит прямые. Поэтому, делаем вывод, что OC является перпендикуляром, который опущенный из точки O на прямую a.
Вот так, только с помощью циркуля и линейки, можно легко построить перпендикулярные прямые. И не важно, где находится точка, через которую должен проходит перпендикуляр, на отрезке или вне этого отрезка, главное в этих случаях верно найти и обозначить первоначальные точки А и В.

На этом уроке мы вспомним понятие прямого угла. Сформируем представления о перпендикулярных прямых. Введем понятия перпендикулярных прямых, перпендикулярных отрезков (или лучей). Узнаем, как определить, что прямые перпендикулярны. А также научимся строить перпендикулярные прямые.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Перпендикулярные прямые"

Разобраться с этой темой нам поможет уже известный вам прямой угол. Напоминаем, что прямой угол – это угол, градусная мера которого равна .

Определение
Две прямые линии, образующие при пересечении прямые углы, называются перпендикулярными.


прямые АВ и СD пересекаются, но не являются перпендикулярными, так как не образуют 4 прямых угла.
А вот прямые AB и EF пересекаются и образуют 4 прямых угла.
Прямые AB и EF называются перпендикулярными.

В математике вы уже не раз встречались с перпендикулярными прямыми.
Например, если продлить смежные (то есть соседние) стороны прямоугольника, то полученные прямые будут перпендикулярны.

Убедиться в том, что две прямые перпендикулярны можно с помощью чертёжного треугольника и с помощью транспортира.

Кроме того строители иногда проверяют перпендикулярность стены основанию дома с помощью грузика, подвешенного на тонкой гибкой нити, т.е. отвеса.
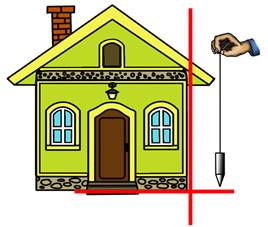
Кстати, латинское “перпендикулярис” означает “отвесной”.
Чтобы убедиться в том, что две прямые перпендикулярны, не обязательно измерять все 4 угла.
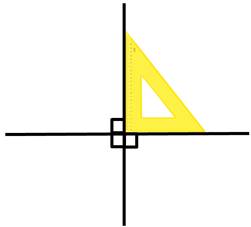
Если один прямой угол, то и три остальных угла тоже будут прямыми.
Например, прямая AD пересекается прямой BC в точке О.
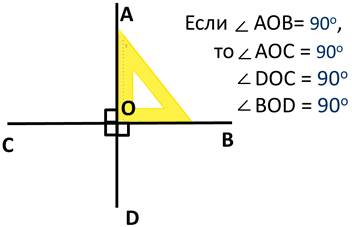
И если угол АОВ прямой, то углы AOC, DOC, BOD прямые.
Построить перпендикулярные прямые не сложно.
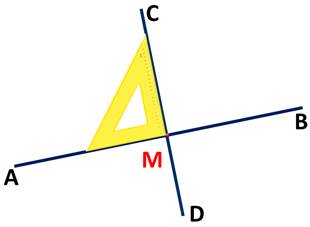
Например, для построения перпендикулярной прямой через точку, лежащую на данной прямой необходимо:
1) построить произвольную прямую АВ, потом отметить на прямой произвольную точку М;
2) взять чертёжный треугольник и совместить сторону прямого угла чертёжного треугольника с прямой АВ, а вершину прямого угла чертежного треугольника с точкой М;
3) провести прямую СD вдоль второй стороны прямого угла чертежного треугольника.
Построение двух перпендикулярных прямых, через точку, лежащую на данной прямой закончено.
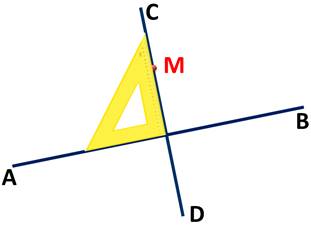
Для построения перпендикулярной прямой через точку, НЕ лежащую на данной прямой необходимо:
1) построить произвольную прямую; отметить точку вне прямой;
2) приложить чертёжный треугольник;
3) провести перпендикулярную прямую.
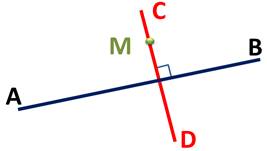
что через любую точку плоскости можно провести единственную прямую, перпендикулярную данной.
Определение
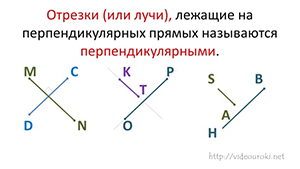
Отрезки (или лучи), лежащие на перпендикулярных прямых называются перпендикулярными.
Например
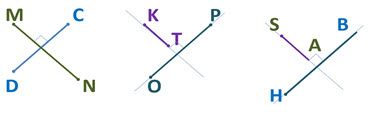
Отрезки MN и CD перпендикулярны.
Отрезки KT и OP тоже перпендикулярны, т.к. через них можно провести перпендикулярные прямые.
Лучи SA и HB лежат на перпендикулярных прямых, а значит перпендикулярны.
Если две прямые перпендикулярны, то при пересечении они образуют углы 90 градусов.
И наоборот, если при пересечении прямые образуют углы 90 градусов, то эти прямые перпендикулярны.

Ключевые слова конспекта: перпендикулярные прямые, перпендикуляр к данной прямой, основание перпендикуляра, существование и единственность перпендикулярной прямой, перпендикулярность и параллельность, существование и единственность перпендикуляра к прямой, расстояние от точки до прямой, расстояние между параллельными прямыми, углы с соответственно перпендикулярными сторонами.
Перпендикулярные прямые — две прямые, которые пересекаются под прямым углом.
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Перпендикуляр к данной прямой — отрезок прямой, перпендикулярной данной прямой, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называют основанием перпендикуляра.
Существование и единственность перпендикулярной прямой.
Через каждую точку прямой можно провести перпендикулярную ей прямую, причем только одну.
Через каждую точку вне данной прямой можно провести перпендикулярную к ней прямую и к тому же только одну.
Перпендикулярность и параллельность.
Две прямые, перпендикулярные третьей, параллельны между собой.
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямой.
Существование и единственность перпендикуляра к прямой.
Из любой точки, не лежащей на данной прямей, можно опустить на эту прямую перпендикуляр и только один.
Расстояние от точки до прямой.
Расстояние от точки до прямой — длина перпендикуляра, опущенного с данной точки на прямую.
Расстояние между параллельными прямыми.
Расстояние между параллельными прямыми — расстояние от любой точки одной прямой до другой прямой.
Углы с соответственно перпендикулярными сторонами.
Углы с соответственно перпендикулярными сторонами или равны, или в сумме составляют 180°.
Перпендикуляр к прямой
Читайте также:


