Как сделать парадокс
Парадокс – это всегда занятная ситуация, которая во многом себе противоречит. Явление, которое может существовать в реальности, но не имеет логического объяснения. Здравый смысл чужд парадоксам, которые нас окружают, тем не менее они очень ценны для развития критического мышления. Мы находим новые пути объяснения различных таинственных явлений, всё дальше продвигаясь к знаниям о мире. Дразнить свой ум и задавать сложные вопросы – это часть большой интеллектуальной деятельности. И чем пристальней ты посмотришь на окружающие тебя вещи, тем больше найдешь удивительного и необъяснимого.
Вот некоторые из самых захватывающих парадоксов на сегодняшний день, о которых ты должен знать. Наслаждайся! Если знаешь ещё какие-нибудь, делись в комментариях.
1. Парадокс Ферми
С одной стороны, выдвигаются многочисленные аргументы о том, что во Вселенной должно существовать значительное количество технологически развитых цивилизаций. С другой стороны, отсутствуют какие-либо наблюдения, которые бы это подтверждали. Ситуация является парадоксальной и приводит к выводу, что или наше понимание природы, или наши наблюдения неполны и ошибочны.
2. Парадокс корабля Тесея
Если описать кратко, то звучит он следующим образом: объект, все компоненты которого заменены, может ли оставаться тем же объектом?
Этот парадокс классический, был пересказан Плутархом. Согласно мифам, корабль, на котором Тесей вернулся с Крита в Афины, хранился афинянами до эпохи Деметрея Фалерского и ежегодно отправлялся со священным посольством на Делос. Но вот в чём суть. Каждый раз перед отправкой в нём заменяли доски. И вот между античными философами возник спор, тот ли это корабль, на котором бороздил моря Тесей, или уже нет? А если построить из старых досок такой же корабль, то тогда какой из них будет настоящим?
3. Парадокс убитого дедушки
Писатель-фантаст Рене Бержавель любил строчить про путешествие во времени, но однажды, в 1943 году, он описал следующий парадокс.
Давай сначала предположим, что путешествие во времени возможно, и у тебя есть специальная машина времени для этого. Ты отправился назад в прошлое и убил своего биологического деда до того, как он встретил твою бабушку. Зачем тебе это делать, мы не знаем. Возможно, ты психически нездоровый психопат, который ненавидит всех людей, которым больше 60. Но не в этом суть. Так вот, ты убил своего дедулю, в результате чего один из твоих родителей никогда не был рождён, а значит и ты не был рождён. Получается, что в конечном итоге ты не смог бы путешествовать во времени, ведь тебя нет, а значит твой дед остался бы жив, а ты, соответственно, был бы рожден, и это позволило бы тебе путешествовать во времени, а значит убить своего деда. Такой вот взрыв мозга.
4. Парадокс всемогущего Бога
Вообще, таких парадоксов целое семейство, но все они сводятся к тому, что может сделать всемогущее существо, и может ли его всемогущество ограничить способность выполнения действий Бога?
Ричард Докинз тем временем отмечает, что всемогущество и всезнание Бога также вступают друг с другом в конфликт: либо Бог знает, что он сделает завтра, либо он имеет свободу (возможность) сделать, что угодно.
5. Парадокс Лжеца
6. Парадокс цирюльника
Очень похож на предыдущий парадокс, да и по сути является интерпретаций парадокса Рассела, который демонстрирует противоречивость логической системы Фреге, что является ранней попыткой формализации наивной теории множеств Г. Кантора. Но не будем углубляться в логику и философию, а раскроем суть парадокса через ситуацию, которую предложил сам Рассел.
7. Парадокс Карри
Ход мыслей, который ведёт к парадоксу, следующий:

Парадоксы — интересная штука и существуют они со времен древних греков. Однако, говорят, что при при помощи логики можно быстро найти фатальный недостаток в парадоксе, который и показывает, почему, казалось бы невозможное, возможно или что весь парадокс просто построен на недостатках мышления.
Опровергнуть парадокс конечно не потяну, мне бы хотя бы понять полностью суть каждого. Это не всегда просто. Вот проверьте…
12. Парадокс Ольберса
В астрофизике и физической космологии парадокс Ольберса – это аргумент, говорящий о том, что темнота ночного неба конфликтует с предположением о бесконечной и вечной статической Вселенной. Это одно из свидетельств нестатической Вселенной, такое как текущая модель Большого взрыва. Об этом аргументе часто говорят как о “темном парадоксе ночного неба”, который гласит, что под любым углом зрения с земли линия видимости закончится, достигнув звезды. Чтобы понять это, мы сравним парадокс с нахождением человека в лесу среди белых деревьев. Если с любой точки зрения линия видимости заканчивается на верхушках деревьев, человек разве продолжает видеть только белый цвет? Это противоречит темноте ночного неба и заставляет многих людей задаться вопросом, почему мы не видим только свет от звезд в ночном небе.
11. Парадокс всемогущества
Парадокс состоит в том, что если существо может выполнять какие-либо действия, то оно может ограничить свою способность выполнять их, следовательно, оно не может выполнять все действия, но, с другой стороны, если оно не может ограничивать свои действия, то это что-то, что оно не может сделать. Это, судя по всему, подразумевает, что способность всемогущего существа ограничивать себя обязательно означает, что оно действительно ограничивает себя. Этот парадокс часто формулируется в терминологии авраамических религий, хотя это и не является обязательным требованием. Одна из версий парадокса всемогущества заключается в так называемом парадоксе о камне: может ли всемогущее существо создать настолько тяжелый камень, что даже оно будет не в состоянии поднять его? Если это так, то существо перестает быть всемогущим, а если нет, то существо не было всемогущим с самого начала. Ответ на парадокс заключается в следующем: наличие слабости, такой как невозможность поднять тяжелый камень, не попадает под категорию всемогущества, хотя определение всемогущества подразумевает отсутствие слабостей.
10. Парадокс Сорита
Парадокс состоит в следующем: рассмотрим кучу песка, из которого постепенно удаляются песчинки. Можно построить рассуждение, используя утверждения: — 1000000 песчинок – это куча песка — куча песка минус одна песчинка – это по-прежнему куча песка. Если без остановки продолжать второе действие, то, в конечном счете, это приведет к тому, что куча будет состоять из одной песчинки. На первый взгляд, есть несколько способов избежать этого заключения. Можно возразить первой предпосылке, сказав, что миллион песчинок – это не куча. Но вместо 1000000 может быть сколь угодно другое большое число, а второе утверждение будет верным при любом числе с любым количеством нулей. Таким образом, ответ должен прямо отрицать существование таких вещей, как куча. Кроме того, кто-то может возразить второй предпосылке, заявив, что она верна не для всех “коллекций зерна” и что удаление одного зерна или песчинки все еще оставляет кучу кучей. Или же может заявить о том, что куча песка может состоять из одной песчинки.
9. Парадокс интересных чисел
Утверждение: не такого понятия, как неинтересное натуральное число. Доказательство от противного: предположим, что у вас есть непустое множество натуральных чисел, которые неинтересны. Благодаря свойствам натуральных чисел, в перечне неинтересных чисел обязательно будет наименьшее число. Будучи наименьшим числом множества его можно было бы определить как интересное в этом наборе неинтересных чисел. Но так как изначально все числа множества были определены как неинтересные, то мы пришли к противоречию, так как наименьшее число не может быть одновременно и интересным, и неинтересным. Поэтому множества неинтересных чисел должны быть пустыми, доказывая, что не существует такого понятия, как неинтересные числа.
8. Парадокс летящей стрелы
Данный парадокс говорит о том, что для того, чтобы произошло движение, объект должен изменить позицию, которую он занимает. В пример приводится движение стрелы. В любой момент времени летящая стрела остается неподвижной, потому как она покоится, а так как она покоится в любой момент времени, значит, она неподвижна всегда. То есть данный парадокс, выдвинутый Зеноном еще в 6 веке, говорит об отсутствии движения как таковом, основываясь на том, что двигающееся тело должно дойти до половины, прежде чем завершить движение. Но так как оно в каждый момент времени неподвижно, оно не может дойти до половины. Этот парадокс также известен как парадокс Флетчера. Стоит отметить, что если предыдущие парадоксы говорили о пространстве, то следующий парадокс – о делении времени не на сегменты, а на точки.
7. Парадокс Ахиллеса и черепахи
В данном парадоксе Ахиллес бежит за черепахой, предварительно дав ей фору в 30 метров. Если предположить, что каждый из бегунов начал бежать с определенной постоянной скоростью (один очень быстро, второй очень медленно), то через некоторое время Ахиллес, пробежав 30 метров, достигнет той точки, от которой двинулась черепаха. За это время черепаха “пробежит” гораздо меньше, скажем, 1 метр. Затем Ахиллесу потребуется еще какое-то время, чтобы преодолеть это расстояние, за которое черепаха продвинется еще дальше. Достигнув третьей точки, в которой побывала черепаха, Ахиллес продвинется дальше, но все равно не нагонит ее. Таким образом, всякий раз, когда Ахиллес будет достигать черепаху, она все равно будет впереди. Таким образом, поскольку существует бесконечное количество точек, которых Ахиллес должен достигнуть, и в которых черепаха уже побывала, он никогда не сможет догнать черепаху. Конечно, логика говорит нам о том, что Ахиллес может догнать черепаху, потому это и является парадоксом. Проблема этого парадокса заключается в том, что в физической реальности невозможно бесконечно пересекать поперечно точки – как вы можете попасть из одной точки бесконечности в другую, не пересекая при этом бесконечность точек? Вы не можете, то есть, это невозможно. Но в математике это не так. Этот парадокс показывает нам, как математика может что-то доказать, но в действительности это не работает. Таким образом, проблема данного парадокса в том, что происходит применение математических правил для нематематических ситуаций, что и делает его неработающим.
6. Парадокс Буриданова осла
Это образное описание человеческой нерешительности. Это относится к парадоксальной ситуации, когда осел, находясь между двумя абсолютно одинаковыми по размеру и качеству стогами сена, будет голодать до смерти, поскольку так и не сможет принять рациональное решение и начать есть. Парадокс назван в честь французского философа 14 века Жана Буридана (Jean Buridan), однако, он не был автором парадокса. Он был известен еще со времен Аристотеля, который в одном из своих трудов рассказывает о человеке, который был голоден и хотел пить, но так как оба чувства были одинаково сильны, а человек находился между едой и питьем, он так и не смог сделать выбора. Буридан, в свою очередь, никогда не говорил о данной проблеме, но затрагивал вопросы о моральном детерминизме, который подразумевал, что человек, столкнувшись с проблемой выбора, безусловно, должен выбирать в сторону большего добра, но Буридан допустил возможность замедления выбора с целью оценки всех возможных преимуществ. Позднее другие авторы отнеслись с сатирой к этой точке зрения, говоря об осле, который столкнувшись с двумя одинаковыми стогами сена, будет голодать, принимая решение.
5. Парадокс неожиданной казни
Судья говорит осужденному, что он будет повешен в полдень в один из рабочих дней на следующей неделе, но день казни будет для заключенного сюрпризом. Он не будет знать точную дату, пока палач в полдень не придет к нему в камеру. После, немного порассуждав, преступник приходит к выводу, что он сможет избежать казни. Его рассуждения можно разделить на несколько частей. Начинает он с того, что его не могут повесить в пятницу, так как если его не повесят в четверг, то пятница уже не будет неожиданностью. Таким образом, пятницу он исключил. Но тогда, так как пятница уже вычеркнута из списка, он пришел к выводу, что он не может быть повешенным и в четверг, потому что если его не повесят в среду, то четверг тоже не будет неожиданностью. Рассуждая аналогичным образом, он последовательно исключил все оставшиеся дни недели. Радостным он ложится спать с уверенностью, что казни не произойдет вовсе. На следующей неделе в полдень среды к нему в камеру пришел палач, поэтому, несмотря на все его рассуждения, он был крайне удивлен. Все, что сказал судья, сбылось.
4. Парадокс парикмахера
Предположим, что существует город с одним мужским парикмахером, и что каждый мужчина в городе бреется налысо: некоторые самостоятельно, некоторые с помощью парикмахера. Кажется разумным предположить, что процесс подчиняется следующему правилу: парикмахер бреет всех мужчин и только тех, кто не бреется сам. Согласно этому сценарию, мы можем задать следующий вопрос: парикмахер бреет себя сам? Однако, спрашивая это, мы понимаем, что ответить на него правильно невозможно: — если парикмахер не бреется сам, он должен соблюдать правила и брить себя сам; — если он бреет себя сам, то по тем же правилам он не должен брить себя сам.
3. Парадокс Эпименида
Этот парадокс вытекает из заявления, в котором Эпименид , противореча общему убеждению Крита, предположил, что Зевс был бессмертным, как в следующем стихотворении: Они создали гробницу для тебя, высший святой Критяне, вечные лжецы, злые звери, рабы живота! Но ты не умер: ты жив и будешь жив всегда, Ибо ты живешь в нас, а мы существуем. Тем не менее, он не осознавал, что называя всех критян лжецами, он невольно и самого себя называл обманщиком, хотя он и “подразумевал”, что все критяне, кроме него. Таким образом, если верить его утверждению, и все критяне лжецы на самом деле, он тоже лжец, а если он лжец, то все критяне говорят правду. Итак, если все критяне говорят правду, то и он в том числе, а это означает, исходя из его стиха, что все критяне лжецы. Таким образом, цепочка рассуждений возвращается в начало.
2. Парадокс Эватла
Это очень старая задача в логике, вытекающая из Древней Греции. Говорят, что знаменитый софист Протагор взял к себе на учение Эватла, при этом, он четко понимал, что ученик сможет заплатить учителю только после того, как он выиграет свое первое дело в суде. Некоторые эксперты утверждают, что Протагор потребовал деньги за обучение сразу же после того, как Эватл закончил свою учебу, другие говорят, что Протагор подождал некоторое время, пока не стало очевидно, что ученик не прикладывает никаких усилий для того, чтобы найти клиентов, третьи же уверены в том, что Эватл очень старался, но клиентов так и не нашел. В любом случае, Протагор решил подать в суд на Эватла, чтобы тот вернул долг. Протагор утверждал, что если он выиграет дело, то ему будут выплачены его деньги. Если бы дело выиграл Эватл, то Протагор по-прежнему должен был получить свои деньги в соответствии с первоначальным договором, потому что это было бы первое выигрышное дело Эватла. Эватл, однако, стоял на том, что если он выиграет, то по решению суда ему не придется платить Протагору. Если, с другой стороны, Протагор выиграет, то Эватл проигрывает свое первое дело, поэтому и не должен ничего платить. Так кто же из мужчин прав?
1. Парадокс непреодолимой силы
Парадокс непреодолимой силы представляет собой классический парадокс, сформулированный как “что происходит, когда непреодолимая сила встречает неподвижный объект?” Парадокс следует воспринимать как логическое упражнение, а не как постулирование возможной реальности. Согласно современным научным пониманиям, никакая сила не является полностью неотразимой, и не существует и быть не может полностью недвижимых объектов, так как даже незначительная сила будет вызывать небольшое ускорение объекта любой массы. Неподвижный предмет должен иметь бесконечную инерцию, а, следовательно, и бесконечную массу. Такой объект будет сжиматься под действием собственной силы тяжести. Непреодолимой силе потребуется бесконечная энергия, которая не существует в конечной Вселенной.
Вот еще некоторые интересные парадоксы, которые мы уже с вами обсуждали: вот например Парадокс Монти Холла, вот Парадокс фитопланктона и муравей на резиновом тросе. Вот еще Занимательные логические парадоксы и C-парадокс. Мало кто верит в Парадокс дней рождения и в подборочку … и гений парадоксов друг !
Парадокс — это утверждение, которое, по-видимому, противоречит само себе и, тем не менее, может быть правдой. Большинство логических парадоксов, как известно, являются неверными аргументами, но, несмотря на это, они важны для продвижения критического мышления. Ниже представлены десять парадоксов, которые совершенно точно удивят вас.

1. Парадокс ценности: Почему вода дешевле, чем бриллианты, ведь для выживания людям нужна вода, а не бриллианты?
Парадокс ценности (также известный как парадокс воды и алмазов, или парадокс Смита) является явным противоречием, состоящим в следующем: несмотря на то, что вода куда более полезна для выживания человека, бриллианты обладают намного более высокой ценой на рынке. На низших уровнях потребления, вода обладает гораздо более высокой предельной полезностью, чем бриллианты, и таким образом, является более ценной. Люди используют воду в больших количествах, чем они используют бриллианты, таким образом, предельная полезность и цена воды ниже, чем у бриллиантов.
При объяснении парадокса алмазов, ученые, изучающие предельную полезность, разъясняют, что в расчёт берётся не общая польза бриллиантов или воды, а польза каждой единицы воды и бриллиантов по отдельности. Абсолютно верно, что совокупная полезность воды имеет огромное значение для людей, так как они нуждаются в ней, чтобы выжить. Однако исходя из того, что воды в мире очень много, предельная полезность воды на самом деле низкая. Другими словами, каждую дополнительную единицу воды, которая становится доступной, можно использовать в менее критических целях, так как основная потребность воды (для выживания) удовлетворена.
Поэтому, любая отдельная единица воды теряет свою ценность из-за того, что в мире есть огромное её количество. С другой стороны бриллиантов в мире очень мало. Их настолько мало, что польза от одного бриллианта во много раз превышает пользу стакана воды, которой в мире очень много. Таким образом, бриллианты обладают гораздо большей ценностью для людей. Поэтому, те люди, которые хотят получить бриллианты согласны платить за них гораздо большую цену, чем за стакан воды, а продавцы бриллиантов устанавливают на каждый бриллиант стоимость, которая намного превышает стоимость стакана воды.
Предполагая наличие причинно-следственной связи между настоящим и будущим путешественника во времени, парадокс убитого дедушки, который нарушает эту связь, может рассматриваться как невозможный (таким образом, предотвращая самовольную переделку чьей-то судьбы). Тем не менее, для избегания парадокса был теоретически допущен ряд гипотез, таких как идея о том, что прошлое нельзя изменить, поэтому дедушка, должно быть, пережил попытку его убийства (как было заявлено ранее). Другая гипотеза состоит в том, что путешественник во времени создаёт или попадает в альтернативную временную линию или параллельную вселенную, в которой сам путешественник никогда не родился.
Вариантом парадокса убитого дедушки является парадокс Гитлера или парадокс убийства Гитлера, довольно часто встречающийся троп в научной фантастике, в котором главный герой отправляется назад во времени, чтобы убить Адольфа Гитлера до того, как он спровоцирует Вторую мировую войну. Вместо того, чтобы обязательно предотвратить путешествие во времени, само действие убирает любую причину это делать, наряду с любой информацией о том, что причина для путешествия во времени когда-либо существовала, изначально убирая, таким образом, любую необходимость в путешествии во времени.
Корабль Тесея (Theseus) это парадокс, который поднимает следующий вопрос: остаётся ли предмет, в котором заменили все составные части, по сути, тем же предметом?
Основываясь на истории можно сделать вывод, что то тело, которое мы видим в зеркале, является абсолютно другим телом по сравнению с тем, что мы видели семь лет назад или ранее, так как клетки человеческого тела регенерируются примерно каждые семь лет.
Первое состоит в том, что некоторые числа являются квадратами, в то время как другие числа ими не являются. Таким образом, всех чисел, включая квадраты и не квадраты, должно быть больше чем просто квадратов. Тем не менее, для каждого квадрата существует одно положительное число, которое является его квадратным корнем, и для каждого положительного числа существует только один квадрат, соответственно, одних не может быть больше, чем других. Это раннее использование, хотя и не первое, идеи о взаимно однозначном соответствии в контексте бесконечного множества. Галилей пришел к выводу, что идеи меньшего, равного, большего относятся к ограниченным, а не бесконечным множествам.

5. Парадокс бережливости: Если все попытаются экономить во время рецессии, совокупный спрос упадет, и общая сумма сэкономленная населением будет меньше
Парадокс бережливости состоит в том, что если все попытаются сэкономить деньги во время экономической рецессии, совокупный спрос упадёт и, в свою очередь, снизит общую сумму, сэкономленную населением, из-за снижения спроса в потреблении и в экономическом росте. Проще говоря, парадокс бережливости, заключается в следующем: общая сумма сэкономленная населением будет меньше, даже в том случае, когда индивидуальные сбережения увеличатся. В более широком смысле, это увеличение индивидуальных сэкономленных сбережений может быть вредоносным для экономики, так как, несмотря на то, что индивидуальная бережливость по общему утверждению является положительной для экономики, в соответствии с парадоксом бережливости – коллективная бережливость может оказать негативное воздействие на экономику. Теоретически, если все люди будут экономить свои сбережения, их объёмы увеличатся, но будет наблюдаться тенденция спада в макроэкономическом статусе.
В этом заключается парадокс брадобрея, который был введён математиком, философом и человеком, отказавшимся исполнять воинскую повинность из Великобритании, по имени Бертран Рассел (Bertrand Russell) в начале двадцатого века. Этот парадокс представил собой огромную задачу, которая изменила всё направление математиков двадцатого века.
По этой и другим причинам, самым популярным решением парадокса Рассела является так называемая аксиоматизация теории множеств Цермело - Френкеля (Zermelo-Fraenkel). Эта аксиоматизация ограничивает предположение наивной теории множеств, согласно которой при наличии условия, всегда можно создать множество, собрав именно те предметы, которые ему соответствуют. Вместо этого, нужно начинать с индивидуальных вещей, создавая множества из них и работая в порядке возрастания. Это означает, что вам не нужно пытаться разделить это множество на те множества, которые содержат самих себя и на те, которые самих себя не содержат. Вам всего лишь нужно сделать это разделения для элементов любого множества, которое вы создали из индивидуальных вещей посредством определённого количества шагов.
Ещё одно возможное (сексистское) решение парадокса заключается в следующем: просто сделайте брадобрея женщиной.

8. Парадокс дней рождения: Как в такой маленькой группе могут быть два человека, родившихся в один день?
Парадокс дней рождения состоит в вероятности того, что во множестве случайно выбранных людей, будут два человека, родившихся в один и тот же день. Согласно принципу Дирихле (pigeonhole principle), эта вероятность достигает 100 процентов, когда количество людей достигает 367 (исходя из того, что существует 366 возможных вариантов дат дней рождения, включая 29 февраля). Тем не менее, вероятность в 99 процентов, достигается, когда множество состоит всего лишь из 57 людей, и 50 процентов, если было собрано 23 человека. Эти выводы включают предположение, что каждый день в году (кроме 29 февраля) в равной степени является вероятной датой дня рождения.
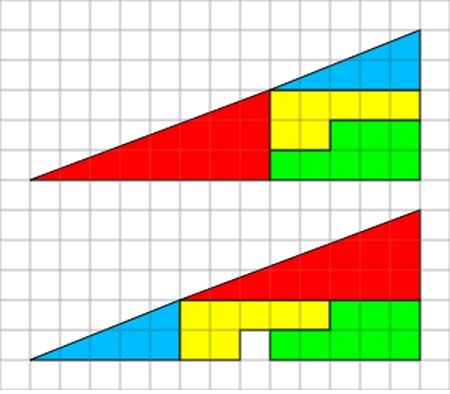
10. Исчезновение клетки: Почему квадрат появляется без видимой причины?
Парадокс исчезновения клетки это оптическая иллюзия, используемая на математических лекциях, чтобы помочь студентам понять геометрические фигуры. Он состоит в описании двух расположений фигурок, состоящих из похожих форм, немного разной конфигурации.

В широком смысле слово парадокс – это явление, ситуация, событие, кажущиеся невероятными и не соответствующие привычным представлениям людей о реальности в силу необычного контекста.
Парадокс — это когда невозможное возможно
Суть парадоксального суждения заключается в том, что начав его рассматривать и исследовать, вы постепенно найдете в нем логику, здравое зерно и придете к умозаключению, что невозможное возможно.
Для лучшего понимания какого-либо термина необходимо обратиться к его антониму (что это такое?). Таковым для парадокса является слово ортодокс – что значит традиционность, постоянство, проверенность. В этом же смысле парадокс описывается как неожиданный, оригинальный, непривычный.
Чтобы предвосхитить путаницу, также следует научиться отличать парадокс от апории. Если первое – это нелогичная правда, то второе – логичная выдумка.
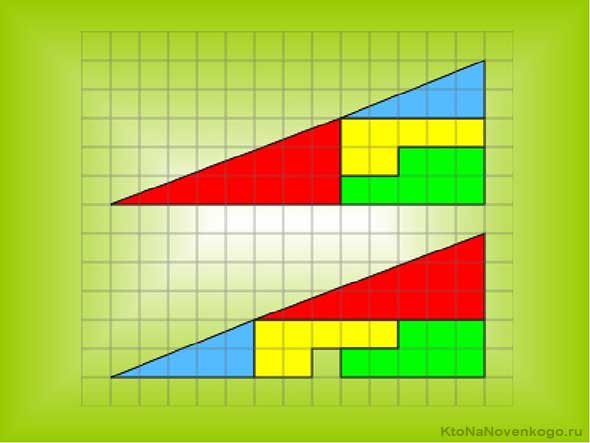
P.S. Если вы не знаете ответ на приведенную выше геометрическую загадку, то не спешите относить ее к теме сегодняшней статьи. Таки нет, это всего лишь апория (ловкий трюк, вводящий в заблуждение). Подробности смотрите ниже (пункт 5 в примерах).
-
В любой науке инструментом для познания и теоретических доказательств является логическое мышление. Экспериментаторы часто обнаруживают парадоксы вследствие появления двух и более результатов исследования, которые противоречат друг другу.
Правда, в некоторых случаях такие расхождения – это всего лишь ошибки, допущенные в ходе экспериментального опыта. Поэтому в научной среде парадокс представляет собой полезное явление, так как мотивирует ученых искать дополнительные методы для изучения теории, минимизировать искажение реальности.
- музыкальные – заключаются в использовании непривычных звуков в отдельности или их фрагментов, резко отличающихся от традиционных;
- художественные – используют писатели, художники, поэты, актеры кино, цирковые деятели, журналисты.
- литературные — например, используемые в тексте или заголовках оксюмороны (словесные парадоксы — несовместимые вещи)
Примеры парадоксов
Чтобы еще лучше понять и усвоить значение этого понятия приведу классические, известные во всем мире примеры.
Далее Ахиллесу нужно преодолеть этот метр, но черепаха уже продвинулась дальше. Каждый раз, когда человек будет достигать крайнюю точку, в которой находилось животное, последнее будет находиться уже в следующей. А так как существует бесконечное число точек, то следуя этой логике, догнать черепаху не представляется возможным.
Эта статья относится к рубрикам:
Комментарии и отзывы (8)
Медицина у нас бесплатная, а без денег не лечат. Образование в стране бесплатное, но каждый месяц нужно платить. А что говорят власти по этому поводу: это парадокс, такого не может быть!)
Я заметила, что люди особенно любят находить парадоксы в том, что касается качества жизни. К примеру, не работает, а деньги всегда есть.
Для меня парадокс — это некая загадка, которой трудно найти логическое объяснение.
Наша жизнь полна парадоксов, а явление это прекрасно тем, что хоть где-то сохраняется интрига))
Юлия, а нет парадокса в том, что люди работают много и получают при этом мало! Они ведь сами настраивают себя на то, что такое положение вещей неизбежно и оно будет всегда. Только сами этого не осознают.
Нет никакого парадокса и в том, что большие деньги зарабатываются легко, так как зарабатывающий их настраивает себя на получение высокой прибыли и верит в то, что по-другому не бывает.
Раньше любил такого рода загадки, но со временем понял, что они только отнимают время и ничего не дают.
1. Курица или яйцо? Процесс установления – генетическая мутация, следовательно первой явилась курица, так как мутация в эмбриональной клетке вероятнее, чем в клетках всей курицы. Курица могла появиться из яйца, но не совсем куриного.
3. Парадокс неожиданной казни. Нарушение логики, а не парадокс. Исключение пятницы предполагает прожитые понедельник — среду и четверг. Не прожил четверг – бойся.
10. Куча – это форма, а не количество.
11. Движение – это изменение положения в промежуток времени. Не в момент, а между двумя моментами.
Читайте также:


