Как сделать открытие в математике
Методы исследования: сбор и анализ информации по теме, составление и решение задач ,обобщение материала. Теоретическая часть исследовательской работы. Составление задач. Практическая часть исследовательской работы. Решение этих задач
если бросать бумажки на дорогу по 5 бумажек в день и не убираться на этой дороге ,то через 365 дней на дороге будет 1825 бумажек.
В лесу примерно 3000 деревьев если их вырубать по 50 деревьев в день то за 2 месяца лес опустеет и останутся только пеньки
в лесу примерно 500 животных если их истреблять по 2 животного в день то через 250 дней животных не останется
В озере примерно 100 рыб если каждый день вылавливать по 5 рыб то через 20 дней их не останется
Если за квартиру надо оплачивать примерно 5000 рублей в месяц и не делать этого, то через 12 месяцев накопится долг в 60000 рублей.
если люди каждый год будут сажать по 367 деревьев то за 8 лет лесу станет 2936 деревьев
если строить по 58 домов в год то через 7 лет вырастет деревня состоящая из 406 домов
Интересные задачи- открытия
Задача №1 Дежурные ушли из класса плохо закрыв кран. Зная, что за 1 секунду вытекает 10г воды, посчитайте, сколько воды утечёт за 1час?
1 час=3600 секунд 36000г=36кг=3 больших ведра На протяжении всей своей истории человечество время от времени страдало из-за нехватки воды. Чтобы не испытывать недостатка в воде даже во время засух, во многих городах и районах стараются ее запасать в водохранилищах и подземных коллекторах, но необходимы и дополнительные сберегающие воду мероприятия, а также её бережный расход. Вывод: Бережем запасы чистой воды.
Задача№2 На школьной аллее 10 молодых деревьев, на каждом дереве 15 веток. Если пятеро друзей будут ежедневно в течении сентября ломать каждый по одной ветке, сколько веток останется на всех деревьях?
15х10-5х30=0 Вывод: Этого допустить нельзя.
А если мы с вами будем любить математику, беречь природу, сажать деревья и цветы, соблюдать чистоту то мир вокруг нас будет вот такой
Выводы: Мир необъятен. Хочется узнавать все больше и больше. А затем все эти полученные знания применить для жизни. Из каждой решенной задачи следует ,что нужно уважать математику как науку ,так как она помогает путем математических расчетов понять как надо жить, а именно :любить и беречь природу, сажать деревья и цветы, соблюдать чистоту и тогда мир вокруг нас будет замечательным. Практическая значимость работы заключается в том, что материалы работы могут быть использованы на уроках математики, биологии, экологии и внеклассных занятиях для учащихся в школе.
По теме: методические разработки, презентации и конспекты
КАК СДЕЛАТЬ УРОКИ МАТЕМАТИКИ НЕСКУЧНЫМИ.
Что же нужно знать тому, кто стремится создать на своих уроках положительную эмоциональную обстановку? Прежде всего, то, что на уроках такой строгой науки, как математика, сделать.
Можно ли сделать уроки математики нескучными

Помогает внимательно слушать рассказ взрослого, отвечать на вопросы по содержанию сказки, не перебивать говорящего, обогощать словарь за счет звукоподражания,воспитывать уверенность в себе.

Открытое занятие "Сделай правильный выбор"
Занятие по здоровому образу жизни, где учащиеся должны приобрести устойчивый навык неприятия к алкоголю, уметь активно противостоять пагубным привычкам; способствовать развитию творческих способ.
Открытое занятие "Как мы Солнцу помогли"
Занятие для инклюзивной группы детей старшего дошкольного и младшего школьного возраста по теме развитие эмпатии.

Открытый урок "Сделаем планету лучше"
Кромсаем лед,Меняем рек теченье,Твердим о том, что дел невпроворот. Но мы еще придем просить прощеньеУ этих рек,БархановИ болот,У самого гигантского восхода,У самого мельчайшего малька. Пока об этом.
Палеонтология, или может ли ребенок сделать открытие
В презентации рассматривается вопрос участия детей в палеонтологических исследованиях и их достижения в этой области.

Временами нам всем было трудно решать математические задачи и запоминать длинный список формул. Но задумывались ли вы когда-нибудь, существует ли этот предмет во Вселенной, ожидая своего открытия? Или кто-то специально придумал его, чтобы наказывать детей? Что ж, ответ на этот вопрос так же сложен, как и математические задачи.
Хотите, верьте, хотите нет, но математика - это центр нашего современного мира. Она также является причиной работы наших смартфонов, автомобилей, зданий и даже погоды. Несмотря на то, что математика существует уже очень давно, между теоретиками математики до сих пор ведутся споры, главным вопросом которых является: была ли математика изобретена или открыта?
Некоторые считают, что математика существует внутри нас, и объекты математики - это наше творение. Другие философы считают, что математика существует независимо от наших мыслей, вне нас. Но не лежит ли истина где-то между этими двумя мнениями: быть изобретенной или открытой? Чтобы узнать истину, давайте разберемся, сколько лет математике?
Сколько лет математике?
История математики так же стара, как и человечество. Она прошла путь от простой математики, такой как подсчет скота, до сложного изучения объекта через абстрактные понятия, которые мы знаем сегодня. Только в 600 г. до н.э., когда возникли цивилизации и появились различные занятия, математика начала свое начальное развитие. Она использовалась для измерения участков, расчета налогов с людей и т.д. Позже, в 500 году до нашей эры, появились римские цифры, которые до сих пор используются для обозначения чисел.
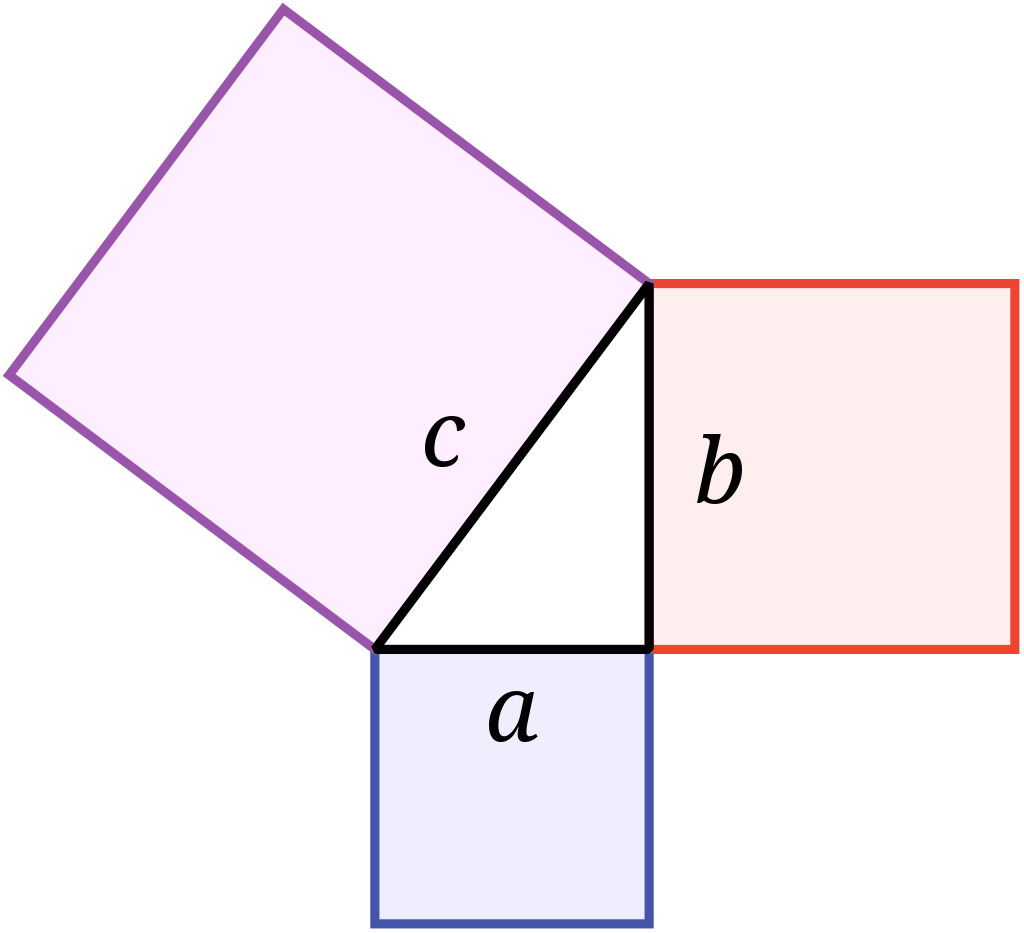
Ученые считают, что тысячи лет назад основные математические функции, такие как сложение и вычитание, могли появиться одновременно в разных местах, таких как Индия, Египет и Месопотамия. Развитая математика появилась в Греции более 2500 лет назад, когда математик Пифагор дал свое знаменитое уравнение. Оно касалось сторон прямоугольного треугольника, которое мы сейчас изучаем как теорему Пифагора.
С тех пор все больше математиков стали работать над расширением своего понимания математики. Однако никто не мог найти единственно верный ответ на главный вопрос.
Существовала ли математика уже во Вселенной?
В прошлом были моменты, когда люди открывали что-то уже существующее, занимаясь математикой, а также времена, когда люди думали, что изобрели уравнения и методы, чтобы записать то, что вертелось у них в голове.
Некоторые люди утверждают, что, в отличие от лампочки, математика была не изобретением, а открытием. Идея заключается в том, что математика существует в разуме Бога или в платоновском мире идей, а мы лишь открываем ее - позиция, известная как платонизм. Она получила свое название от имени древнегреческого мыслителя и математика Платона. Он считал, что математические сущности абстрактны и существуют независимо в своем мире, вне пространства и времени.

Платон - древнегреческий философ и математик.
Некоторые математические идеи настолько фундаментальны, что, даже если бы вы не открыли их, кто-то другой открыл бы их. Математика - это язык науки, и ее структуры являются врожденными для природы. Даже если бы завтра вселенная исчезла, вечная математическая истина все равно бы существовала. Мы должны открыть ее, понять ее функционирование и, опираясь на наши знания, найти решения для физических явлений, которыми мы стремимся управлять.
Многие математики поддерживают эту точку зрения. Они открыли множество вечных истин, не зависящих от разума, который их обнаружил. Например, не существует наибольшего простого числа, число "пи", выраженное в десятичных дробях, может продолжаться бесконечно.
Математика проявляется в природе и дает ответы на многие универсальные вопросы. Одним из примеров того, как математику можно найти в природе, является золотое сечение.
Золотое сечение и последовательность Фибоначчи
Золотое сечение описывает наиболее предсказуемые закономерности во Вселенной. Оно описывает все - от атомов, формы урагана, лица и человеческого тела до галактики. Золотое сечение - это когда отношение частей (a) и (b) равно (a + b), деленное на большую часть (a). Она имеет значение около 1,618 и обозначается греческим алфавитом фи, Φ. Она также известна как божественная пропорция.
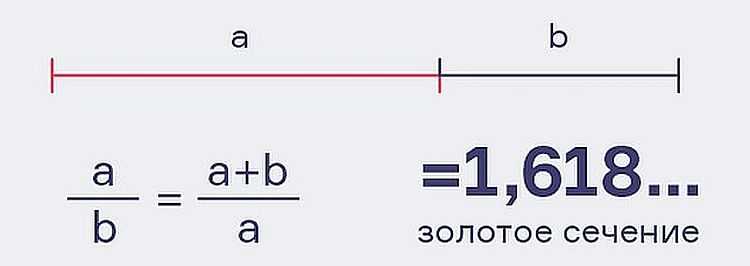
Золотое сечение было получено из последовательности Фибоначчи, названной в честь итальянского математика Леонардо Фибоначчи. На протяжении сотен лет последовательность Фибоначчи очаровывала многих математиков, ученых и художников. Таким образом, последовательность будет выглядеть следующим образом: 0,1,1,2,3,5,8,13,21,34,55. и так далее.
Последовательность Фибоначчи можно увидеть в различных предметах вокруг нас, например, в ракушках, животных, пирамидах и других неожиданных местах.

Золотое сечение в природе
Лепестки цветов также следуют последовательности Фибоначчи. Если вы понаблюдаете, то количество лепестков в цветке будет одним из следующих: 3,5,8,13,21,34 или 55. Например, у лилии 3 лепестка, у космеи 8 лепестков, у ноготков 13 лепестков, у цикория и маргаритки 21 лепесток, а у дикой астры 55 лепестков. Это подтверждает аргумент о том, что математические функции существовали в природе, а мы лишь открыли их.
Была ли математика нашим творением?
Некоторые люди выступают против идеи о том, что математика была открыта. Они принадлежат к антиплатонической школе мысли, которая считает, что математика была изобретена. Они считают, что математика - это человеческое изобретение, созданное таким образом, чтобы адекватно описывать физический мир. Чтобы удовлетворить наши потребности, человеческий разум продолжает создавать математические понятия.
Если бы завтра исчезла Вселенная, то исчезли бы все выдуманные идеи, такие как футбол, шахматы или любое другое занятие, придуманное нами, исчезла бы и математика.
Люди поняли принцип работы Вселенной, просто наблюдая за закономерностями, которые появляются в природе. Мы придумали математические понятия, абстрагируя такие элементы, как формы, линии, группы и т.д. из окружающего нас мира, и установили связи между этими понятиями либо для достижения какой-то цели, либо просто для развлечения.
Геометрия и арифметика были разработаны благодаря нашей способности наблюдать и различать такие формы, как круги, треугольники и т.д. А также различать прямые и кривые линии.
Вначале мы использовали натуральные числа - 1,2,3. - для подсчета окружающих нас предметов. Позже мы придумали дополнительные понятия, такие как отрицательные целые числа, рациональные и иррациональные числа, комплексные числа и многие другие. Эти расширения математики были разработаны, чтобы служить нашим целям.
Допустим, температура на ртути опустилась ниже 0. Чтобы проиллюстрировать число ниже нуля, мы используем отрицательные целые числа и пишем -10 °С или -25 °С. Благодаря этому процессу изобретения новых идей на основе того, что мы видим вокруг себя, не будет неправильным сказать, что математика родилась из наших представлений и мысленных картин.
Спор между теми, кто считает математику открытием, и теми, кто считает ее изобретением, может продолжаться вечно. Учитывая, что проблема существует уже 2 300 лет, вряд ли эта загадка разрешится в ближайшее время. Но правда остается в том, что математике просто все равно, верим ли мы, что она была изобретена, открыта или оба сыграли роль в ее существовании. Независимо от наших убеждений, она будет объективно выполнять свою функцию.

Осуждённый на 25 лет тюрьмы парень, затосковав в одиночной камере, нашёл отдушину в цифрах и всерьёз увлёкся математикой. За несколько лет заключения он настолько преисполнился в своём познании, что сделал математическое открытие. Теперь арестант — без пяти минут учёный, причём без аттестата об окончании средней школы.
Кристофер Хевенс, отбывающий 25-летний срок за убийство в исправительном учреждении Вашингтона, стал автором математического открытия, пишет Popular Mechanics. Парень был осуждён ещё в 2011 году и, сидя в одиночной камере, увлёкся цифрами, открыв для себя своё истинное призвание.
В тюрьме у Кристофера не было ни подходящих учебников, ни учителей, а до ареста он не занимался научной деятельностью. Поэтому заключённому пришлось искать помощь извне.
В январе 2013 года мой партнёр Мэтью Карго, который был в то время выпускающим редактором журнала Mathematical Science Publishers, получил пересланное письмо от коллеги, — вспоминает доктор химии из Университета Торонто Марта Черрути.

Это было одно из писем, которые рассылал Кристофер, чтобы получить доступ к научному математическому журналу Annals of Mathematics.
Для тех, кого это может интересовать, я ищу дополнительную информацию о подписке на журнал Annals of Mathematics для личного использования. На данный момент я отбываю 25-летний срок в исправительном учреждении Вашингтона, и я решил использовать это время для самосовершенствования. Я учусь исчислению и теории чисел, потому что работа с цифрами стала моей миссией. Не могли бы вы, пожалуйста, прислать мне информацию о вашем журнале? — написал заключённый.
В постскриптуме парень добавил, что обучаться без нужных материалов и учителей не так уж и легко, поэтому ему приходится иногда подолгу задерживаться на некоторых темах. Кристофер спросил, не мог бы кто-нибудь из математиков периодически с ним переписываться, и заранее поблагодарил адресатов.
После этого начался его путь к успеху. Мэтью Карго помог заключённому связаться с родителями Марты Черрути, которые были математиками.
Изначально мой отец Умберто Черрути, теоретик чисел, который был профессором в Туринском Университете, согласился помочь Кристоферу только потому, что тот попросил. Мой отец думал, что Кристофер был одним из тех чудаков, которые влюбляются в числа и строят ошибочную теорию.
Чтобы проверить знания заключённого, Умберто отправил ему задачу для решения и был очень удивлён, когда получил в ответ лист бумаги длиной в 120 сантиметров. В этом письме была длинная и сложная формула, но выяснилось, что старался Кристофер не зря.
Мой отец ввёл формулу в свой компьютер, и, к его удивлению, результаты оказались верными.
После этого Умберто привлёк заключённого к работе над проблемой, связанной с непрерывными дробями, которой занимался сам. И не пожалел об этом. Спустя годы обмена идеями с учёным арестант стал автором математического открытия. Его выводы были опубликованы в журнале Researcher in Number Theory в январе 2020 года.
В этой работе впервые были показаны некоторые закономерности аппроксимации огромного класса чисел. Кристофер выявил их с помощью ручки и бумаги, а также благодаря возможности обмениваться письмами с соавторами из Италии.
После того как научная статья, где в списке авторов первым числится Кристофер, увидела свет, заключённый пообщался с Мартой Черрути и рассказал, как вообще пришёл к математике.
Парень рассказал, что до тюрьмы он не был большим фанатом учёбы и даже аттестат об окончании школы не получил.
Образование давалось мне с трудом. Я не окончил среднюю школу — наркоман без работы и без места, которое мог назвать домом. Образование трудно получить в тюрьме. Поэтому я искал за её пределами. Я стараюсь строить мосты и развивать свои отношения с людьми снаружи. Потому что это моё образование.
Кристофер видит в математике свой способ отдать долг обществу, в то же время понимая, что за такое преступление нельзя расплатиться и до конца жизни.
Я наметил долгосрочный план жизни, чтобы приспособиться к выплате долга, у которого нет цены. Может быть, это прозвучит глупо, но я отбываю свой срок в обществе души своей жертвы. Я посвящаю ему большую часть своих самых крупных достижений, — рассказал он Марте по телефону.
После тюрьмы Кристофер планирует продолжить заниматься наукой. В настоящее время он поступает в университет, который может помочь ему получить степень доцента онлайн.
Среди заключённых, как показывает практика, немало умных парней, но применяют свои способности они далеко не всегда в соответствии с законом. Арестант придумал, как использовать медицинскую маску для побега, и лайфхак оказался настолько гениален, что беглеца так и не поймали.
Но иногда даже гениев подводят мелочи. Другой заключённый создал идеальный план по собственному освобождению, но исполнить его помешала маленькая орфографическая ошибка.
Кто-то уже давно назвал математику основой всех наук. С этим трудно поспорить, ведь без математических знаний невозможно описать ни движение планет, ни полёт бабочки. Более того, без этих знаний трудно даже подсчитать, на что потратить свои карманные деньги, или сколько дней осталось до очередного отпуска! Если хоть чуточку задуматься, величие и всеохватность математических знаний поражают. Кто же они — великие математики и их открытия, кто подарил человечеству эту науку?
Отцы-основатели
Эвклид

Пифагор
Если Эвклид — отец геометрии, то Пифагора величают отцом математики. Он также жил в Греции, за полторы сотни лет до Эвклида. Создал собственную математическую школу, впервые в истории человечества сделал математику прикладной наукой, вводя её элементы в повседневный обиход. Кстати, далеко не все историки согласны с тем, что именно он доказал свою знаменитую тригонометрическую теорему.

Архимед

Математики Возрождения
После заката эллинической культуры математика Европы пережила несколько веков стагнации, пока новая плеяда умов не вдохнула в эту науку новые идеи. Назвать выдающихся математиков того времени намного сложнее, потому что их оказалось значительно больше, чем в Древней Греции.
Леонардо Пизанский
В европейской науке более известен как Фибоначчи. Жил и умер в городе Пиза (последняя треть XII - первая четверть XIII веков). Его отец, известный торговец, страстно хотел, чтобы сын продолжил семейное дело, поэтому брал юношу в далёкие поездки на Ближний Восток и даже в Северную Индию.
Здесь Леонардо познакомился с индийской и арабской математическими школами, которые в эти века значительно превосходили уровень европейской математики.

Исаак Ньютон (1642 — 1727 гг.)

Готфрид Лейбниц (1646 — 1716 гг.)
Этот немецкий учёный жил и творил в одно время с Ньютоном, и, независимо от последнего, создал основы математического анализа, опирающиеся на понятия бесконечно малых величин. Лейбниц представлял себе матанализ алгебраически, а не кинематически, как это делал Ньютон.

Леонард Эйлер (1707 — 1783 гг.)
В специальной литературе нередко можно встретить утверждение, что этот швейцарец является самым выдающимся математиком всех времён. Между прочим, он много лет прожил в России, в Петербурге, и даже многие свои работы написал на русском языке, который выучил в совершенстве всего за год!

Рене Декарт (1596 — 1650 гг.)
Когда мы говорили, что Ньютон и Лейбниц разработали основы математического анализа, справедливо было бы вспомнить, что их изыскания базировались не на пустом месте. Начальные идеи были известны ещё до работ этих учёных, а разработал их почти легендарный француз, Рене Декарт.

Жозеф Луи Лагранж (1736 — 1813 гг.)

Пьер-Симон Лаплас (1749 — 1827 гг.)
Много работал как астроном, но в математике известен как один из тех, кто разрабатывал теорию вероятностей. Специалистам известны уравнения его имени и преобразование Лапласа. Ввёл важное понятие математического ожидания.

Иоганн Гаусс (1777 — 1855 гг.)

Российские математики
В заключение хотелось бы подчеркнуть, что свой вклад, причём значительный, внесли в европейскую математическую науку и российские учёные. Вспомним хотя бы о некоторых их них.
Николай Лобачевский (1792 — 1856 гг.)
Создал особый раздел в геометрии, до сих пор называемый неэвклидовой геометрией, или попросту, геометрией Лобачевского. Его труды, не признанные современниками, опередили своё время, изменили традиционное представление о пространстве и заложили фундамент для работ Эйнштейна. Также уточнил понятие непрерывной функции, разработал несколько остроумных теорем о тригонометрических рядах.

Софья Ковалевская (1850 — 1891 гг.)
Первая женщина в России, ставшая профессором математики. Много работала в области небесной механики и математической физики, описывала вращение твёрдого тела, решила одну из так называемых задач Коши.

Андрей Колмогоров (1903 — 1987 гг.)
Один из тех учёных, кто разработал теорию вероятностей в её современном виде. В своих трудах добился фундаментальных результатов в функциональном анализе, теориях множеств, мере и приближение функций.


На вопросы Научной России отвечали:
— доктор физико-математических наук, сотрудник МФТИ, РЭШ, ЦЭМИ РАН, автор более ста научно-популярных курсов по математике Алексей Савватеев.
Сложности популяризации математики
Несмотря на то, что все мы в школе, хотели мы того или нет, занимались математикой очень много, мы не изучили и сотой доли всех тех понятий и даже общих закономерностей, что существует в этой науке. А значит, уже начав разбираться с каким-то исследованием, мы натолкнемся на то, что не понимаем даже слов, что употребляет ученый.
Еще одна сложность, о которой говорят многие математики, занимающиеся популяризацией — страх перед этой наукой, укоренившийся у многих еще со школы. Отчасти он связан с проблемами преподавания математики в школе, а отчасти со вполне объективной сложностью этой науки.
Революция, которую никто не замечает
Итак, великие открытия, которые мы не заметили — это Проблема четырех красок, Великая теорема Ферма, Гипотеза Пуанкаре и проблема узлов. Памятуя о сложностях перевода с математического языка на русский обывательский, попробуем хотя бы кратко рассказать о том, что это за открытия.

Теорема о четырех красках была сформулирована в 1852 году и доказана только в 1976 году, став, кстати, первой значимой теоремой, доказанной при помощи компьютера. Согласно этой теореме, всякую расположенную на сфере карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета.
Читайте также:


