Как сделать остроугольный треугольник

В школьном курсе геометрии изучают разные виды треугольников. В задачах очень часто рассматривают остроугольный треугольник, поэтому стоит особенно пристально изучить свойства этой фигуры.

Определение понятия
Треугольником называют фигуру, состоящую из трех точек, и трех отрезков их соединяющих. В зависимости от углов треугольник может быть:
- Прямоугольным, если один из углов равен 90 градусов;
- Тупоугольный, если один из углов тупой, т.е. больше 90 градусов;
- Остроугольным, если все углы треугольника острые.
Для решения задач с остроугольными треугольниками часто приходится использовать теорему синусов или косинусов.
Еще в Древней Греции математики изучали треугольники. Именно греки разработали основы современной геометрии, куда входит и множество теорем о треугольниках. Например, автор теоремы Пифагора родом из Древней Греции.
Характеристики
В остроугольном треугольнике каждый угол меньше 90 градусов. Но сумма углов в треугольнике всегда равна 180. В любой фигуре вершины обозначают заглавными латинскими буквами.
Одним из элементов треугольника, вместе со сторонами и углами, является внешний угол. Внешний угол это угол, смежный с внутренним углом треугольника.
У любого треугольника 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым.
Линии остроугольного треугольника
Остроугольный треугольник обладает рядом свойств.
Медиана геометрической фигуры будет делить сторону, на которую она опущена, пополам. Причем можно провести этот отрезок с любой вершины. Медианы пересекаются в одной точке, и эта точка делит каждую из них в отношении 2:1.

Рис. 1. Медианы в остроугольном треугольнике
Известно, что если провести три высоты в остроугольном треугольнике, то они будут пересекаться в одной точке, которую называют ортоцентром. Эти отрезки опускают под прямым углом к противоположным сторонам. Высоты в остроугольном треугольнике разделяют эту фигуру на прямоугольные треугольники.
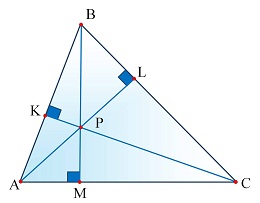
Рис. 2. Высоты в остроугольном треугольнике
Биссектрисы в остроугольном треугольнике не только делят углы пополам. Эти отрезки пересекаются в точке, которая является центром вписанной окружности.
Также биссектриса разделяет сторону остроугольного треугольника на две части, которые пропорциональны соответствующим боковым сторонам. Данное утверждение нужно запомнить, чтобы решать некоторые задачи.
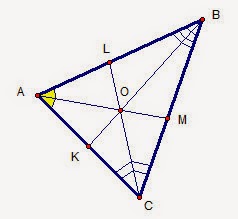
Рис. 3. Биссектрисы в остроугольном треугольнике
Свойства
Если суммировать числовые значения любых двух сторон остроугольного треугольника, то обязательно получим цифру, которая будет больше третьего отрезка данной геометрической фигуры.
Средняя линия в остроугольном треугольнике параллельна одной из сторон данной фигуры и равна ее половине.
Что мы узнали?
В остроугольном треугольнике каждый угол меньше 90 градусов. Общая сумма углов здесь также равняется 180 градусов. Нельзя забывать о характерных линиях треугольника. Поскольку с их помощью легко вычислить стороны данной треугольной фигуры или центр определенной окружности. А если в условиях задач по геометрии указаны углы, то можно воспользоваться тригонометрическими функциями.
9. Начертите остроугольный треугольник АВС. Постройте тупоугольный треугольник с основанием АС и тупым углом при вершине С, такой, чтобы его высота, опущенная на прямую АС, была равна высоте данного треугольника, проведенной из вершины В.

9. Начертите остроугольный треугольник АВС. Продлите сторону
АС за точку С на CF = АС В точке F восставьте перпендикуляр FK,
равный ВН (ВН ⊥ АС). Соедините точки К и А. ∆АСК — искомый

На данном уроке мы даём определения остроугольному, прямоугольному и тупоугольному треугольникам. Более подробно останавливаемся на прямоугольном треугольнике. И как всегда решаем задачи, применяя полученные теоретические знания.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Остроугольный, прямоугольный и тупоугольный треугольники"
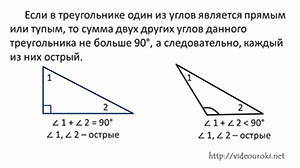
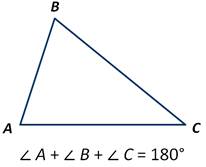
Теорема о сумме углов треугольника:
Сумма углов треугольника равна 180 градусов.
Из теоремы следует, что если в треугольнике один из углов является прямым или тупым, то сумма двух других углов данного треугольника не больше 90 градусов, а следовательно, каждый из них острый.
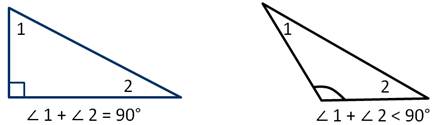
По величине углов выделяют следующие виды треугольников.
Остроугольный треугольник - это треугольник, у которого все три угла острые.
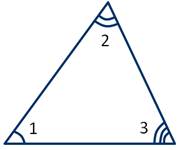
Тупоугольный треугольник - это треугольник, у которого один из углов тупой.
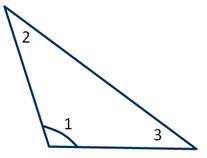
Прямоугольный треугольник - это треугольник, у которого один из его углов является прямым.
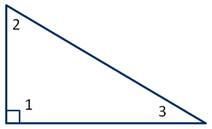
Нужно знать, что стороны прямоугольного треугольника имеют специальные названия.
Итак, две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
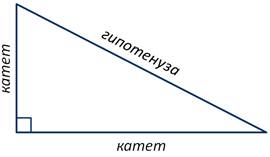
Если взять прямоугольный лист бумаги и разрезать его, получим:

Получим две модели прямоугольного треугольника.
Доказать, что угол с вершиной на окружности, опирающийся на диаметр, - прямой.
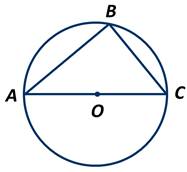
Для начала соединим точку В с точкой О, которая является центром нашей окружности. Так как отрезки ОА, ОВ и ОС равны как радиусы окружности, то треугольники АОВ и ВОС являются равнобедренными. А значит, у них углы при основаниях равны. Обозначим градусные меры этих углов m и n. Тогда ∠АОВ=2n, так как он является внешним углом треугольника ВОС, смежным с ∠ВОС. А нам известно, что внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
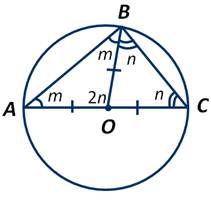
А так как сумма углов треугольника равна 180 градусов, то:
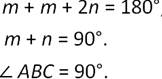
Что и требовалось доказать.
Доказать, что если в равнобедренном треугольнике АВС один из углов равен 60 градусов, то он равносторонний.
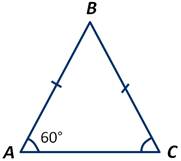
Если ∠А при основании равнобедренного треугольника АВС равен 60 градусов, то и второй ∠С при основании равен 60 градусам. Получаем:
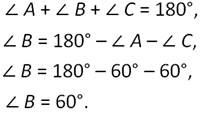
Следовательно, треугольник АВС равносторонний.
Пусть ∠В при вершине равнобедренного треугольника АВС равен 60 градусам. Тогда получим:
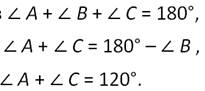
А так как углы А и С- углы при основании равнобедренного треугольника, то они равны между собой и равны 60 градусам. А следовательно, и в этом случае треугольник АВС является равносторонним. Что и требовалось доказать.
Доказать, что в прямоугольном треугольнике АВС медиана, проведённая к гипотенузе АВ, равна половине гипотенузы.
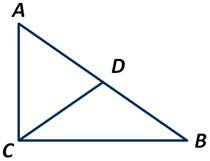
Отложив ∠2=∠1, получаем:
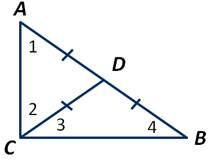
Треугольник ADC является равнобедренным. А следовательно, отрезок DA=DC.
Так как по условию угол АВС - прямой, то:
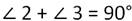
Известно, что сумма острых углов прямоугольного треугольника равна 90 градусов, то есть:
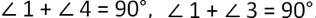
Тогда из равенств получаем:
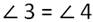
Из этого следует, что ВСD равнобедренный треугольник, у которого стороны DB и DC равны.
Следовательно, СD - медиана и СD равняется половине гипотенузы АВ. Что и требовалось доказать.
Треугольники различаются между собой по характеру углов и по характеру сторон.
Виды треугольников по углам
- Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
- Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°.

Виды треугольников по сторонам
- Разносторонний треугольник – это треугольник, у которого все стороны имеют разную длину.
- Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой.
Читайте также:


