Как сделать оси в аксонометрии с помощью циркуля
Публикации для людей, интересующихся наукой и техникой
Мысленное воспроизведение формы и размеров сложной детали, изделия, сборочной единицы не всегда достигается по проекционному чертежу. В этом случае на помощь проекционному чертежу приходят аксонометрические проекции, т.е. изображения, на которых деталь, изделие, сборочная единица воспринимаются наглядно, объемно.
Известно, что предметы окружающего нас мира являются трехмерными, имея некоторые размеры по высоте, длине, ширине. При построении ортогонального проекционного изображения одно из измерений всегда вырождается, поскольку направление проецирования совпадает с одним из направлений мерности. Поэтому ортогональный проекционный чертеж позволяет судить о двух измерениях.
Кроме того, плоские контуры, изображаемых в проекционном чертеже геометрических образов, часто выглядят отрезками прямых, что также затрудняет мысленное воспроизведение формы. Аксонометрические проекции лишены этого недостатка, ибо геометрический образ проецируется на плоскость так, что ни одно из измерений не вырождается в точку и изображение дает все три измерения (высоту, длину, ширину), что приводит к объемному восприятию. Объемное изображение в большей степени передает информацию о форме и пропорциях детали, изделия, сборочной единицы, нежели проекционный чертеж.
Аксонометрические проекции не заменяют проекционного чертежа, а только его дополняют. Аксонометрия – не самоцель, её построение весьма сложно, и она требуется лишь тогда, когда по проекционному чертежу весьма трудно представить форму изображенного геометрического образа.
При выполнении рабочих чертежей деталей, вопрос о необходимости исполнения той или иной детали в аксонометрии решается ведущим преподавателем. При конструировании же новых деталей машин и механизмов аксонометрические проекции используются обязательно.
Вполне очевидно, что умение правильно выбрать вид аксонометрии, знать различные приемы построения в аксонометрии и, наконец, обладать навыками построения деталей машин и механизмов в аксонометрии совершенно необходимы будущему инженеру.
Очень часто в практике проецирования, наряду с изображением предмета в системе ортогональных проекций, возникает необходимость наглядных видов.

Аксонометрия поможет лучше понять форму конструкций, их взаимодействие, а также общую форму здания и его внешний вид. Поэтому любой грамотный инженер–конструктор должен хорошо владеть техникой построения аксонометрии и уметь пользоваться ею.
Аксонометрический чертеж только тогда будет обратимым, если для любой точки изображенного на нем объекта можно построить ее основание (вторичную проекцию). Плоскость, на которую проецируется заданный объект, называется аксонометрической плоскостью проекций. Плоскость проекций можно выбирать вполне произвольно. Направление проецирования также выбирается произвольно. Например, мы можем проецировать заданный объект лучами, перпендикулярными к выбранной плоскости проекций. В этом случае аксонометрия называется ортогональной.

ВИДЫ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
Аксонометрические проекции называют прямоугольными если направление проецирования и проецирующие прямые перпендикулярны плоскости, на которую они проецируются, и косоугольными если направление проецирования не перпендикулярно плоскости аксонометрических проекций. Проекции аксонометрических осей на плоскость называют аксонометрическими осями, а проекции единицы измерения по осям – аксонометрическими единицами измерения.
В зависимости от положения предмета и осей координат относительно плоскости проекций, а также в зависимости от направления проецирования единицы измерения проецируются в общем случае с искажением. Искажаются и размеры проецируемых предметов. Отношение длины аксонометрической единицы к ее истинной величине называют показателем или коэффициентом искажения для данной оси координат.
Аксонометрические проекции называют изометрическими, если коэффициенты искажения по всем осям равны; ди метрическими, если коэффициенты искажения по двум осям равны и триметрическими, если все коэффициенты различны. Для аксонометрических изображений предметов применяют пять видов аксонометрических проекций: прямоугольные – изометрические и ди метрические, косоугольные – фронтальные ди метрические, фронтальные изометрически и горизонтальные изометрические.
ХАРАКТЕРНЫЕ ПОСТРОЕНИЯ В АКСОНОМЕТРИИ
Реальные детали машин и механизмов представляют собой, как правило, комбинации и сочетания различных геометрических образов, которые при взаимном пересечении образуют линии перехода. Эти линии могут быть как пространственными, так и плоскими. Умение строить эти линии в аксонометрии является совершенно необходимым, ибо в противном случае нельзя правильно передать форму изображаемой детали. Чтобы построить наглядное изображение линии перехода двух геометрических образов, прежде всего необходимо построить проекции этой линии. Общие точки искомой линии находятся, как правило, с помощью вспомогательных секущих плоскостей, чаще всего – плоскостей уровня. Разумеется, что секущие плоскости нужно выбрать так, чтобы они пересекали конкурирующие поверхности по простейшим линиям (прямым или окружностям).
В рассматриваемом примере линии среза в пространстве являются гиперболами, аксонометрические проекции которых тоже являются гиперболами.
Во всех остальных случаях, аксонометрическая проекция линии среза строится с помощью дополнительных сечений, а если поверхность вращения является линейчатой – с помощью образующих.


Получить консультацию или заказать выполнение задания по аксонометрическим и изометрическим проекциям можно здесь.
ВИД ПРАВИЛЬНЫХ И НЕПРАВИЛЬНЫХ ГЕОМЕТРИЧЕСКИХ ТЕЛ В АКСОНОМЕТРИИ
Геометрические образы правильной формы (многогранники и поверхности вращения – прямой круговой цилиндр, прямой круговой конус, сфера, правильные призмы и пирамиды) часто встречаются в реальных деталях машин и механизмов. Правильные геометрические тела характеризуется наличием в них различных осей и плоскостей симметрии, что позволяет строить аксонометрические изображения этих тел по принципу симметрии.
Допустим, требуется построить аксонометрическое изображение прямой шестигранной пирамиды. Прежде всего отнесем рассматриваемый геометрический образ к системе прямоугольных координат, выбрав положение осей так, чтобы они лежали в соответствующих плоскостях симметрии. При таком положении осей видно, что элементы геометрического образа располагаются симметрично относительно плоскостей Р и Q и, следовательно, относительно осей ОХ и ОУ. Строим аксонометрические оси (например, для ортогональной изометрии) и на этих осях откладываем точки 1, 4 по оси OX и a, b по оси OY.

На горизонтальной проекции геометрического образа эти точки располагаются симметрично относительно осей ОХ и ОY (или относительно начало осей точки О). Следовательно, в аксонометрии они располагаются таким же образом.
Строим стороны основания 23 и 56, которые параллельны оси ОХ, так как их проекции параллельны этой же оси. Найдя аксонометрическое положение вершины S, строим полную аксонометрическую проекцию данного геометрического образа.
Принцип симметрии используется для построения наглядных изображений любых правильных многогранников Построение наглядных изображений правильных поверхностей вращения несколько отлично от рассмотренного, т.к. в основе этих поверхностей лежат окружности, аксонометрические проекции которых изображаются эллипсами.
Выполнение деталей в аксонометрии поясним на примере выполнения корпуса вентиля. Даны вертикальная и горизонтальная проекции детали. Построение аксонометрического изображения начинаем с выбора вида аксонометрической проекции. Для данного геометрического образа удобнее использовать изометрию, так как все окружности, лежащие в различных плоскостях, будут изображаться одинаковыми по форме эллипсами. Построение начинаем с вычерчивания осей Х, Y, Z. По оси Х симметрично точке О1 откладываем отрезок 12, который соответствует длине корпуса, т.е. определяем положение левого и правого торцов боковых фланцев. Из начала координат проводим окружность, радиус которой равен 1,22 радиуса центральной внешней сферы корпуса, а по оси Z – расстояние 03', это будет центр верхнего торца корпуса, проецирующего тоже в эллипс, большая ось которого будет перпендикулярна оси Z1.

Далее и соответственно по оси Х1 и Z1 строим внутренние торцы фланцев, с помощью отрезков 14, 25, 36 находим центры искомых эллипсов. И, наконец, пристраиваем цилиндрические патрубки фланцев, примыкающие к сферической части корпуса. Изображаемая деталь требует построения разреза в аксонометрии, который может быть выполнен двумя парами секущих плоскостей: 1-ая пара – фронтальная и профильная плоскости, 2-ая пара – фронтальная и горизонтальная плоскости. Остановимся на первом варианте (введем плоскости S1 и S2).

Плоскость S1 пересекает цилиндрические поверхности фланцев и патрубков по образующим АВ и CD…, а сферическую поверхность по окружностям (эллипсам). Плоскость S2 пересекает сферическую поверхность также по окружностям (эллипсам), а вертикальный патрубок и горизонтальный фланец по образующим.
Как начертить изометрию?

Практически все, кому довелось изучать черчение и инженерную графику сталкивались с необходимостью произвести построение изометрической проекции детали. В этом уроке мы попробуем разобрать основные моменты, которые нужно знать, чтоб начертить изометрию. Уверен, что повторив указанные в этом уроке шаги, вы сможете самостоятельно выполнить и более сложное задание. В вашей детали может быть большее количество построений, но основные принципы останутся неизменными. Но при этом оговорюсь, что построение изометрии скорее всего будет вам не под силу, если вы еще не освоили построение третьего вида и построение простого разреза. Вы должны уже уметь хорошо ориентироваться в трех видах на чертеже.
Начнем с того, что определимся с направлением осей в изометрии.
На следующей схеме показано соответствие направлений, по которым откладываются размеры в изометрии по отношению к размерам на чертеже. Интересный момент: как показал опыт, этот рисунок кому-то помогает понять принцип построения, а кого-то - наоборот - ставит в тупик. Поэтому, если вас эта схема скорее смущает, нежели просветляет, не зацикливайтесь на нем и читайте дальше - вполне вероятно, что там все будет понятно.
На этом закончим вступительную часть и начнем непосредственно построение изометрической проекции детали. Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.
Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.
Мы получили верхнюю грань фигуры. Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом - в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. Изображение окружностей на всех трех плоскостях я описал в отдельном уроке, а пока лишь скажу, что в изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b - вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм).
Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра - по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена - не хватает только прямоугольного сквозного отверстия.
Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия - по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.
На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху - в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.
Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).
Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!
Следующий шаг в черчении: Уникальный урок на тему "Как начертить диметрию детали?"
Вы можете сказать "спасибо!" автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект "White Bird. Чертежи Студентам"
или запишите наш телефон и расскажите о нас своим друзьям - кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки - и кто-то еще сможет освоить черчение.
А вот это - не реклама. Это напоминание, что каждый из нас может сделать. Если хотите - это просьба. Мы действительно им нужны:
Автор комментария: светка
Дата: 2010-09-08
пипец. я ни чего не понимаю. а завтра экзамен. ((((
Мы стараемся. Правда. Но в то же время мы понимаем, что написать понятно для всех не сможем. Что поделаешь. Однако, мы стремимся оформлять статьи по начертательной геометрии, а так же статьи по инженерной графике в максимально информативном и доступном виде.
Автор комментария: гринкс
Дата: 2010-09-28
хорошо что у меня завтра не экзамен. а лишь занятие по черчению. Со второго прочтения разобрался и смог начертить изометрию своей детали, надеюсь что правильно :))) Спасибо
Автор комментария: Антон
Дата: 2010-10-14
В музыкальном колледже требуют изометрический чертёж.Я бы лучше концерт сыграл.Черчение для меня-полная тьма.
Да уж. Неисповедимы пути. Я бы тоже концерт сыграл. Но вот к сожалению черчу лучше, чем музицирую. Не отчаивайтесь! Звоните, если не разберетесь. Удачи! Антон.
Автор комментария: Елена
Дата: 2010-10-21
замечательно.всё так понятно и просто
Автор комментария: Андрес
Дата: 2010-11-28
Огромное вам спасибо, вспомнил азы=)
Автор комментария: Диана
Дата: 2011-11-25
помогите начертить изометрию
Автор комментария: Диана
Дата: 2011-11-25
Антон спасибо большое за внимание. я уже все поняла. а вы физику хорошо знаете??
Автор комментария: оля
Дата: 2012-02-17
тут хоть понятно)
Автор комментария: михаил
Дата: 2012-06-09
здравствуйте ! нужен чертеж спичечьного коробка в изометрической и диметрической проекции !
Эх, жаль ваш вопрос пришел в момент когда я был в отпуске. Изометрия спичечного коробка еще не встречалась мне в заданиях, хоть это и несложно, но все же какое-никакое разнообразие.
Автор комментария: Андрей
Дата: 2012-06-19
Блин завтра экзамен . Эту то деталь я понял как начертить, а вот смогу ли я начертить деталь из билета .
Андрей, надеюсь у вас все получилось. Но пожалуй, действительно, пришла пора сделать второй урок объясняющий построение изометрии детали приближенной к заданиям среднего уровня сложности. Жаль, что вам это уже не пригодится, но благодаря вам многим станет легче.
Автор комментария: Виктор
Дата: 2012-09-15
Спасибо, что напомнил. Я сто лет уже изометрию не чертил, хотя и работаю инженером
Автор комментария: Яна
Дата: 2012-11-18
надо ли чертить все отверстия если они одинаковые? например 5 отверстий под винты. Или достаточно обозначить их оси?
На учебные чертежи нет ГОСТов. Есть разрешенные допущения. И их количество в каждом ВУЗе свое. В вашем случае правильным будет согласовать с преподавателем, либо выполнить все отверстия.
Автор комментария: Свелана
Дата: 2012-11-19
Статья отличная,большое спасибо, всё прояснилось) Скажите, вы писали выше в коментариях, что нужно сделать изометрию детали средней сложности, не появилась ещё?
Светлана, все произошло немного по-другому. Я взял среднюю деталь, имеющую несколько окружностей в своих формах и создал по ней урок. "Как начертить диметрию?" :))) Ссылка на него находится в самом конце статьи, до комментариев. Я считаю, что он может серьезно углубить ваши знания в части понимания, как чертить аксонометрические проекции разных деталей.
Автор комментария: 9th
Дата: 2012-12-26
Офигенно. Спасибо, с первого раза всё понял.
Автор комментария: Семен
Дата: 2013-02-10
Вы маги чтоль? как вы смогли обьяснить столь бестолковому человеку такую не простую вещь?))
Семен, хотел ответить, что "нет, я только учусь!" Но это больно уж избито :) Маги? Нет. Просто мне хочется сделать жизнь вокруг меня хоть немного лучше. И если у меня есть возможность хоть немного повлиять на количество покупаемых студенческих работ, заменив уставших и разлюбивших свою работу преподавателей - я пытаюсь это сделать. Ну а вам - всего наилучшего!
Автор комментария: Александр
Дата: 2013-03-03
Ребят спасибо! Объяснено очень доходчиво, более лучшего объяснения не встречал!
Хорошо, коль так! Учитесь на здоровье!
Автор комментария: Золушка
Дата: 2013-03-05
СпасиБо! Можно двигаться дальше благодаря Вам! Появился свет в конце тоннеля!;)))
Автор комментария: Кирюха
Дата: 2013-03-17
Спасибо, все отлично написано, понятно. Особый респект автору. Еще хотелось бы узнать как показать резбу на валу в изометрической проекции.
Автор комментария: Лена
Дата: 2013-04-21
Спасибо большое. Все очень ясно изложено)
Автор комментария: Ольга
Дата: 2013-05-05
Спасибо огромное. Теперь все стало понятно, и я начертила деталь по контрольной.
Автор комментария: Серёга
Дата: 2013-06-02
Спасибо, что-то понял.
Автор комментария: MARUFJN
Дата: 2013-07-20
Автор комментария: АЙОГА
Дата: 2014-02-20
Автор комментария: Пётр
Дата: 2014-02-28
Скажите пожалуйста это в каком учебном заведении ещё есть черчение Я учусь в техническом Вузе и черчения нету
Петр, напишу в ответ следующее: МГТУ им. Н.Э Баумана, МИФИ, МАМИ, МАДИ, РХТУ, МИРЭА, МЭИ, МГУГиК, МГСУ, МАТИ, РУДН, РГУ Нефти и Газа им. Губкина, МГУПИ, МГОУ, МИСИ - вот неполный список московских ВУЗов, в которых не забыли, что такое подготовка полноценного инженера. Удачи!
Автор комментария: Татьяна
Дата: 2014-03-13
Спасибо вам большое,очень помогли,без вашего урока бы не справилась,все объяснено доходчиво и по существу,очень благодарна)))
Автор комментария: Вита
Дата: 2014-05-15
очень хорошая статья, не могли бы вы добавить изометрию шестиугольной призмы?очень надо!
Автор комментария: Марина
Дата: 2014-05-21
Большое спасибо. Знаю автокад для геологии, а черчение для меня вообще Луна, в вузе не было. Но благодаря объяснениям смогла сделать. Побольше бы таких толковых авторов. Еще раз огромное спасибо, спасли мне оценки ребенка
Автор комментария: Хама
Дата: 2014-11-04
Туфта! Размеры граней откладываются с коэффициентом 0,82 сторона не 50 мм а уже будет 0,82*50=41 хаваете инфу за должное.
ОК, расшифрую замечание внимательного читателя. В прямоугольной изометрической проекции действительные искажения по осям (по всем трем) и в самом деле равны 0,82. Но поскольку мы не оторваны от земли, и разбираемся с тем, как начертить домашнее задание, а не пишем реферат по черчению (!), то мы используем приведенные коэффициенты, равные единице. Я за 18 лет практики не встречал ни одного ВУЗа в нашей стране, где бы требовались коэффициенты 0,82. Поэтому рисуем с коэффициентом искажения по осям 1, но для энциклопедических знаний запоминаем 0,82. Не исключено, что этот вопрос когда-то будет задан в какой-нибудь телевикторине.
Автор комментария: Алексей
Дата: 2014-12-22
Начертите изометрию куба со стороной 80 мм и в каждой видимой гране впишите овал
Замечательное задание из замечательного ИКСИ? Так там же ничего сложного - просто аккуратно выполняете построения - только циркуль и только линейка.
Автор комментария: Антон
Дата: 2014-12-24
Огромное спасибо. Чудесное объяснение. Даже я понял. :)
Автор комментария: Человек
Дата: 2015-01-15
Автор комментария: Альбина
Дата: 2015-02-08
Большое спасибо, очень помогли! Сыну нужно было начертить изометрию, на уроке ничего не понял, я уже все забыла. Вместе с ним разобрались благодаря вашим объяснениям, очень доступно.
Автор комментария: Денис
Дата: 2015-03-11
Нужно ли заштриховывать ребро жесткости при сечении?
Денис, в изометрии всегда штрихую разрез вне зависимости от того, идет ли он через ребро жесткости. Так учили меня в свое время на кафедре черчения. Я готов предположить, что кто-то из преподавателей в каком-либо ВУЗе может считать иначе. В любом случае, стереть тонкие линии штриховки не составит труда. Но скорее всего стирать их не придется.
Автор комментария: Дмитрий
Дата: 2015-04-15
Очень бы хотелось видеть данный урок в pdf или doc формате. А в общем спасибо за урок!
Автор комментария: николай
Дата: 2015-11-17
Пользуйтесь на здоровье!
Автор комментария: Асхат Сабен
Дата: 2015-11-27
Я учусь в 9 классе. У нас есть урок черчения. Я №1 в классе по ЧЕРЧЕНИЯ! Я хочу стать архитектором. По этому я хочу узнать все подробности.
Вы один из очень небольшого количества современных школьников, кому довелось встретить черчение до ВУЗа. Поверьте, вам будут завидовать все ваши одногруппники на первом курсе :) А в целом - наличие цели и желание ее добиться - это здорово. Я поделился чем смог - пользуйтесь и добрым словом поминайте :)
Автор комментария: Михаил
Дата: 2015-11-30
Автор комментария: Анатолий
Дата: 2015-12-01
Это не изометрия, а аксонометрия.Есть ещё и диметрия.
Анатолий, на всякий случай попробую систематизировать ваши знания. Смотрите. Есть такая штука, называется аксонометрические проекции. Оно же аксонометрия. К ним относятся такие виды проекций как изометрия и диметрия. И еще несколько их подвидов. Но в целом - это же хорошо, что вы ищете. Главное - не перепутать ничего и правильно запомнить.
Автор комментария: Михаил
Дата: 2015-12-09
Ваш сайт первый по запросу в гугле. Что ж, совсем не зря! И разобрали как раз мой вариант. Спасибо за вашу работу!
Вот это я понимаю, вот это повезло :) А ведь деталь из головы брал! Но, как я понимаю, вы еще и суть теперь знаете, а это очень хорошо! Да, не зря я работал над оптимизацией, не зря!
Автор комментария: Сергей
Дата: 2016-01-10
Здравствуйте! А моему мнению,в чертеже с вырезанной четвертью, допущена неточность!
Сергей, приветствую! На картинке с вырезанной четвертью наверняка есть "неточности". Например нет штриховки, какие-то разноцветные линии, торчащие не по ГОСТу осевые. Но урок-то был о другом. Пусть пока остается как есть.
Автор комментария: Светлана
Дата: 2016-04-27
Хочу сказать спасибо за работу.Вы мне очень помогли .Ещё раз спасибо.
Спасибо, всё поняла (хотя черчение проходила в школе лет 40 назад))). Сейчас помогаю сыну. Предлагаю и Вам помощь: редактировать тексты перед публикацией на предмет знаков препинания (для лучшего понимания такой полезной информации!). С уважением! Успехов.
Автор комментария: Зоя
Дата: 2016-12-16
Давно уже не чертила изометрию, все забыла. Благодарю за отличный урок!
Автор комментария: Дан
Дата: 2017-01-08
Спасибо за это объяснение, лично мне аксанометрия нравится, но в отверстиях на плоскости малек туплю,блин архитектору это нужно. Спасибо вам)
Спасибо за объяснение,все четко показано
Спасибо огромное. Учителя объясняют тему не понятно, а здесь всё ясно и понятно
Спасибо большое! Хоть вспомнил правила изометрии. А то работаю авиационным инженером, завтра самолет строить, а я позабыл изометрические коэффициенты)))
такая себе хорактеристика азаметрий
Автор комментария: Андрей
Дата: 2019-07-10
Я, конечно, изучал изометрию почти 15 лет назад, но у Вас в финальном чертеже с разрезом есть ошибка. По условиям вертикальное отверстие сквозное, а на чертеже сделано не правильно. У вас это отверстие "уходит" дальше размеров самой детали. Как-то так.
Автор комментария: Андрей
Дата: 2019-07-10
Поправочка: всё правильно. Совпадают вертикальные линии задней стенки с разрезом. Изометрия такая изометрия. Пока не измерил в живую, не увидел. Конечно перспектива в этом плане более информативна.
Автор комментария: Владимир
Дата: 2020-07-31
ого, я уже забыл все что мы проходили на уроках черчения в школе, оказывается.
Автор комментария: LeOn4iK
Дата: 2020-11-15
Очень круто, мне понравилось!
Автор комментария: Александр
Дата: 2021-03-20
Сам учился в строительном, со временем что-то забывается, 30 лет прошло. Для детей и внуков приходится заглядывать. БлагоДарствую за толковое разъяснение, даже для школьников
Бро, это было 11 лет назад.
Добавьте свой комментарий:
Наша страница в ВК:
Антон, у вас офис только в Москве? или в других городах тоже есть?
Валерий, в настоящее время мы не имеем региональных представительств. Хорошо это или нет - не знаю. Сейчас для удаленных пользователей доступны только услуги по выполнению чертежей в электронном виде
MorozArt Studio © 2005 • 2011 • Москва • Удаленная работа
При публикации статей с сайта активная ссылка на оригинал обязательна.
Аксонометрические проекции применяют, чтобы передать на чертеже представление о форме предмета с разных сторон. При этом вид предмета с разных сторон проецируется на плоскости куба. Наклон плоскостей в аксонометрической проекции придает окружности форму эллипса. Из-за трудности построения эллипсов на практике их заменяют овалами.
- Как построить окружность в аксонометрии
- Как строить аксонометрию
- Как построить окружность в изометрии
- Лист бумаги, карандаш, циркуль, транспортир, линейка или угольник.
Построить окружность в аксонометрии помогает квадрат, в который вписана заданная окружность. На плоскости под наклоном квадрат принимает форму ромба. Поэтому сначала постройте в нужной плоскости ромб. Его стороны должны быть равны диаметру окружности и параллельны соответствующим осям проекции. Центр ромба должен совпадать с центром окружности.
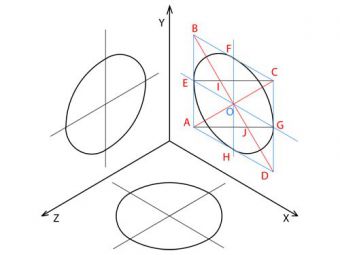
Последовательно обозначьте углы построенного ромба точками A, B, C и D. При этом точка A должна располагаться в том углу ромба, который наиболее близок к точке пересечения осей на аксонометрической проекции.
Начертите диагонали получившегося ромба, соединив отрезками точки A и C, а также B и D. Диагональ AC образует малую ось овала, а диагональ BD – большую.
Проведите через центр ромба O две линии, которые параллельны осям проекции и разделяют ромб на 4 части.
Последовательно обозначьте точки, в которых линии параллельные осям проекции пересекают стороны ромба буквами E, F, G и H. Точка E должна следовать за точкой A в том же направлении, в котором последовательно обозначались углы ромба.
Обозначьте точки, в которых большая ось ромба пересекает отрезки AG и EC буквами I и J. При этом точка I должна лежать на отрезке EC, а точка J на отрезке EC.
С помощью циркуля начертите дугу между точками E и F. Центр окружности для дуги расположен в точке I, а её радиус равен длине отрезка EI. Аналогично начертите дугу между точками G и H.
Начертите две дуги, которые закончат построение овала на проекции. Первая дуга с центром окружности в точке A соединяет точки F и G. Радиус первой дуги равен длине отрезка AG. Вторая дуга с центром окружности, который расположен в точке C, соединяет точки E и H. Ее радиус равен отрезку EC. Когда вы закончите чертить вторую дугу, вы получите построенную окружность на плоскости аксонометрической проекции.
Лекальная кривая строится по точкам, которые затем плавно соединяются от руки или при помощи лекала (способ 1).
Циркульная кривая строится при помощи циркуля как кривая, состоящая из четырёх сопрягающихся дуг окружностей (способы 2, 3).
Рассмотрим построение эллипса в аксонометрической плоскости х'О'у'. Аналогичными будут построения в других плоскостях. Только необходимо учитывать ориентацию осей эллипса. Возьмём окружность произвольного радиуса и построим её прямоугольную изометрию и диметрию разными способами, заготовив предварительно треугольники пропорциональности (рис. 84).
Способ L Лекальная кривая. Строим аксонометрию по восьми точкам, которыми будут являться концы осей и сопряжённых диаметров.


В прямоугольной изометрии (рис. 85, а) приведённые коэффициенты искажения по всем осям равны 1. Поэтому на осях х' и у' от центра О' откладываем радиус 7? окружности, на оси г' - малую полуось эллипса 0,717?, на прямой, перпендикулярной z', - большую его полуось 1,22R.
Для определения размеров большой и малой полуосей эллипса откладываем на натуральной шкале (1:1) треугольника пропорциональности для изометрии радиус окружности R, и из точки А проецируем его на остальные шкалы. На верхней шкале получаем размер 1,227?, на нижней - 0,71 R.
В прямоугольной диметрии (рис. 85, 6) по осям х' и z' коэффициент искажения равен 7, по оси у-0,5. Поэтому на оси х' откладываем радиус R. Остальные размеры определяем при помощи треугольника пропорциональности для диметрии. На натуральной шкале (1:1) откладываем радиус R и через точку А и конец этого отрезка проводим проецирующий луч. На шкале 0,5 получаем размер 0,57? для оси у на шкале 0,35 - размер 0,357? малой полуоси эллипса, который откладываем на z'. Размер 1,067? большой полуоси берём со шкалы 1,06 и откладываем его на прямой, перпендикулярной z'.
Полученные восемь точек в обоих случаях предпочтительнее соединить при помощи лекала.

Примечание. Размеры осей эллипса для прямоугольной изометрии можно определить и графически (рис. 86). Для этого из концов С и D взаимно перпендикулярных диаметров окружности проводим дуги радиусом CD до взаимного пересечения в точках А и В. Соединив точки А и В, получим большую ось эллипса, равную 1,22D, а отрезок CD будет его малой осью, равной 0,7 Ш.
Способ 2. Коробовая кривая. Коробовая кривая является циркульной кривой, состоящей из четырёх дуг окружностей (рис. 87). Ею можно заменить эллипс. Строится она по его осям.
На рис. 87 коробовая кривая построена в прямоугольной изометрии. Малая ось CD направлена вдоль аксонометрической оси z большая АВ ей перпендикулярна. Построение выполняем в определённой последовательности.
- • Соединяем концы большой и малой полуосей (отрезок A Q.
- • Находим разность большой и малой полуосей (отрезок СЕ). Для этого из центра О' радиусом О'А проводим дугу до пересечения с прямой, проходящей через CD, в точке Е.
- • Откладываем СЕ от точки С на АС. Получаем точку F.
- • Строим срединный перпендикуляр к отрезку AF и отмечаем точки пересечения его с прямыми линиями, проходящими через оси эллипса. 0 и 02 - центры двух дуг окружностей.
- • Замеряем расстояния от 0 и 02 до О'и откладываем их по другую сторону от центра эллипса 2 = 0'04). Получаем ещё два центра 03 и 04.
- • Соединяем попарно центры и проводим дуги из центра 0 радиусом 0А, из 02 - радиусом 02С, из 03 - радиусом 02В и из 04 - радиусом 04D. Точки сопряжения дуг находятся на линиях центров.
На рис. 88 построена прямоугольная диметрия окружности в плоскости x'O'z' в виде коробовой кривой. Малая ось CD направлена вдоль оси у' и равна 0,95D. Большая ось АВ ±у' и равна 1,060. Последовательность построения та же, что была рассмотрена выше для изометрии.
Этот метод является универсальным и может применяться не только для построения аксонометрии окружности, но и любого эллипса или овала, если известны размеры его большой и малой оси, чем широко пользуются при конструировании технических деталей.
Способ 3. Овал. Построим прямоугольную изометрию окружности в плоскости х'О'у', заменяя эллипс овалом (рис. 89)
Задаём аксонометрические оси х', у', z' и направление большой оси эллипса (перпендикулярно z'). Из центра эллипса проводим окружность радиусом, равным радиусу той окружности, аксонометрию которой строим. На пересечении этой окружности с направлением малой оси эллипса (осью z') получаем два центра дуг 0 и 02. Проводим прямые через 0 и точки Е, L (или через 02 и точки К, F) пересечения окружности с осями х', у'. На пересечении их с направлением большой оси получаем ещё два центра - 03 и 04. Затем последовательно проводим из центра 0 дугу EL радиусом 0Е, из центра 04 - дугу LF радиусом Оф?, из 02 - дугу FK радиусом 02F, из 03 - дугу КЕ радиусом 02К. Построенный овал неточно повторяет форму эллипса. У них имеются небольшие расхождения в размерах. Таким приёмом можно построить овал только в прямоугольной изометрии.
На рис. 90 показано построение овала, заменяющего эллипс в прямоугольной диметрии. Овал строится по осям и пригоден только для эллипсов, у которых малая ось в три раза меньше большой оси (в плоскостях х'О'у'иг'ОУ). Рассмотрим построение овала в плоскости х'О'у'.
Проводим две взаимно перпендикулярные прямые. Одну вертикально (параллельно z% другую горизонтально. Точка пересечения прямых будет центром О эллипса. Отрезки АВ и CD - соответственно большая и малая ось эллипса. По обе стороны от центра О на прямой, проходящей через малую ось CD, откладываем отрезки, равные длине большой оси АВ эллипса. Получаем центры 0 и 02 двух дуг окружностей. Центры 03 и 04 двух других дуг окружностей удалены от концов А и В большой оси эллипса на расстояние 1/4CD. Соединяем попарно центры и между линиями центров проводим дуги: из 0 радиусом Оф, из 04 радиусом О4В, из 02 радиусом 02С, из 03 радиусом 6М. Как следует из построений, радиусы сопрягающихся дуг равны R = АВ + 1/2CD, г = 1/4CZ).
Коробовая кривая и овал представляют собой кривые, приближенные к эллипсу. Существуют и другие способы построения эллипса.
Лист 1. Тема урока: Построение окружности в аксонометрии.
Лист 2. Фронтальная диметрическая проекция (см. рис. 18.1).


Рис. 18.1 Рис. 18.2
Лист 3. Изометрическая проекция (см. рис. 18.2).
Лист 4. Центровые оси (см. рис. 18.3). Для выполнения построений учащимся выдаются распечатанные заготовки (см. приложение 8).


Рис. 18.3 Рис. 18.4
Лист 5. Обозначения осей для построения овала в плоскости V, W, H (см. рис. 18.4).


Рис. 18.5 Рис. 18.6
Лист 6-7. Построение овала в горизонтальной плоскости проекции. Обозначение оси Z – главная ось (см. рис. 18.5), на пересечении окружности и осевой обозначаем точки (см. рис. 18.6), из них проводим вспомогательные радиусы (синие стрелки) до пересечения с осевыми линиями (см. рис. 18.7).


Рис. 18.8 Рис. 18.9


Рис. 18.10 Рис. 18.11
Строим две малые дуги овала. Центры малых дуг лежат на пересечении двух левых и двух правых стрелок. Радиус равен остатку стрелки (см. рис. 18.10). Овал в горизонтальной плоскости построен (см. рис. 18.11).
Лист 15 – 20. Построение овала во фронтальной плоскости проекции. Обозначение оси Y – главная ось (см. рис. 18.12), на пересечении окружности и осевой обозначаем точки (см. рис. 18.13), из них проводим вспомогательные радиусы до пересечения с осевыми линиями (см. рис. 18.14). Строим большие дуги овала (см. рис. 18.15). Затем малые дуги овала (см. рис. 18.16).


Рис. 18.12 Рис. 18.13



Рис.18.14 Рис.18.15 Рис. 18.16
Лист 21 – 25. Построение овала в профильной плоскости проекции. Обозначение оси X – главная ось, на пересечении окружности и осевой обозначаем точки, из них проводим вспомогательные радиусы до пересечения с осевыми линиями.


Рис. 18.17 Рис. 18.18



Рис. 18.19 Рис. 18.20 Рис. 18.21
Лист 26. Домашнее задание (см. рис. 18.22).
Читайте также:


