Как сделать октаэдр
В данной статье мы рассмотрим, как собрать бумажный октаэдр, что эта фигура собой представляет и чем она может быть полезна для каждого из нас. Возможно, кто-то найдет себя в подобном виде творчества или же наконец-то получит вариант самодельного подарка близкому человеку. Инструкция по изготовлению этой стереометрической фигуры проста, и с ней справится даже ребенок дошкольного возраста, поэтому поехали.

Начинаем собирать фигуру
Многие, глядя на октаэдр в развертке, недоумевают, как правильно соединить между собой все его грани и стороны, чтобы фигура приобрела правильный внешний вид. Попробуем раскрыть эту геометрическую тайну и понять, как собрать бумажный октаэдр. Для начала нам понадобится сама фигура в развертке. Ее можно переснять из книги или же распечатать изображение, которое приложено к статье. Можно сказать, что это есть готовая схема. Как сделать октаэдр самостоятельно? Это также несложно. За основу возьмите любую величину, которая вам потребуется. Это будет длина каждой грани фигуры. Затем прорисуйте шесть равносторонних треугольников так, как вы их видите на рисунке, а к ним дорисуйте еще два.
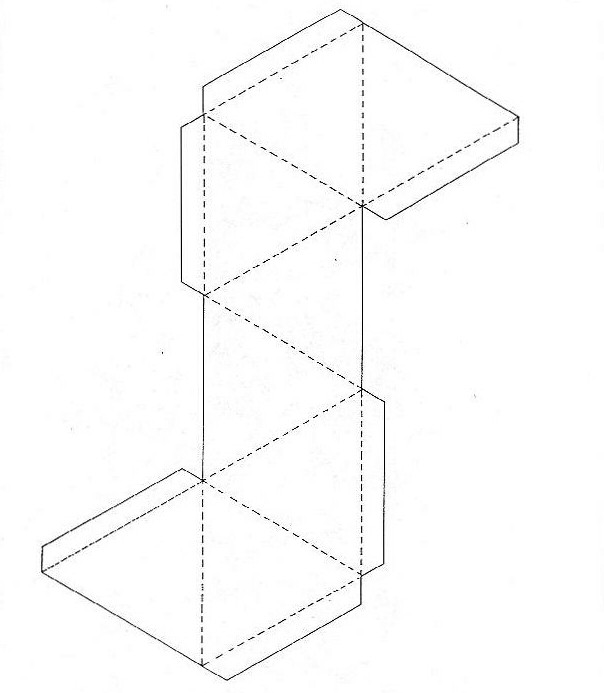
Особенности монтажа граней
Многие даже после того, как построят развертку фигуры, не понимают, как собрать бумажный октаэдр так, чтобы он получился правильным. Для этого нужно, вырезая фигуру, оставить припуски для склеивания. Они имеют скошенные края, и на одном из рисунков они изображены. Теперь наносим на эти припуски клей и собираем стереометрическую фигуру по линиям сгиба. Важно, чтобы вы предварительно проделали четкие сгибы в месте пересечения всех граней фигуры. Так ваша поделка будет иметь более красивый и точный, с геометрической точки зрения, внешний вид.
Нужные навыки
Когда вы знаете, как собрать бумажный октаэдр, вам проще работать с более сложными геометрическими фигурами. Некоторым людям это необходимо для работы, другие просто пополняют свой багаж знаний и расширяют творческий диапазон таким образом. Стоит отметить, что собирать эту поделку можно из обыкновенной тонкой бумаги, если вы тренируетесь. Когда октаэдр нужен для каких-либо других целей, желательно использовать ватман или плотный картон.

Полезные геометрические сувениры
Обучение и хобби
Во многих дошкольных заведениях детей учат тому, как рисовать стереометрические фигуры в развертке, а после этого собирать их и склеивать. Если вы видите, что у вашего ребенка подобных навыков нет, обучите его всему этому на дому. Также если в данной области пробелы имеются у вас, вы всегда можете наверстать упущенное и, распечатав приложенную схему, собрать бумажный октаэдр с помощью обычного канцелярского набора.
Октаэдр - один из пяти выпуклых правильных многогранников.

Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.
Википедия расскажет вам о вычислении площади октаэдра и других Платоновых телах.

Или сохраните развёртки октаэдра в jpg-формате:
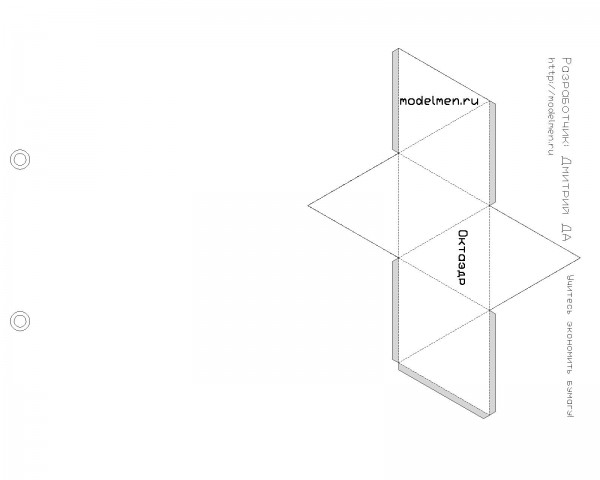
КОММЕНТАРИИ
у меня получилось, спс большое,только было бы лучше если можно было бы распичатать по честям
ничего не получилась!! не октаэдр,а какой-то прямоугольник у которого одна часть больше другой.
У меня получился довольно таки симпотяшный октаэдр и довольно просто его было сделать спс большое. Александр если руки и одного сета и мозгов нету то тогда тебе не одна инструкция и формула не поможет.
Отличный получился октаэдр :) Спасибо большое!
норм вийшло спс
Классный октаэдр, всё довольно легко и быстро) Спасибо огромное;))
Все получилось , спасибо за чертеж , а у которых не получается значит руки кривые .
Развертка норм, но потратил часа полтора
Спасибо огромное! Всё делал сам, чертил, вырезал и клеил!) Отличный получился октаэдр! Такой же, как на картинке! Сделал за 25 минут.
как его сделать
Отстой,углы вообще не сходятся.
Я ищу я делаю А вы как там
вы народ сколько там сантиметров пожалеть Подскажите
Круто!! Всё получилось
Спасибо большое. Скачивать не стала, стало интересно начертить самостоятельно . Все получилось идеально!
Чтобы понять как нарисовать октаэдр, нужно представлять что есть октаэдр. Октаэдр это многогранник имеющий 8 граней. В качестве граней в октаэдре выступают правильные (равносторонние) треугольники. Нарисовать октаэдр не сложно и сейчас я вам покажу как нарисовать октаэдр в тетради по шагам.
Так же в конце статьи вы найдёте ссылку для скачивания pdf-файла с развёрткой октаэдра для склейки на листе формата A4. Переходите на домашнюю страницу Страны советов, чтобы узнать больше интересных историй.
Пошаговый туториал
Шаг 1
Нарисуйте вспомогательные линии, точка пересечения будет центром нашего октаэдра.
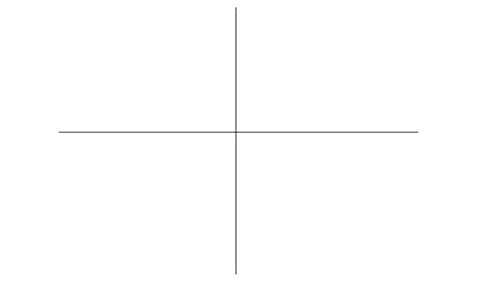
Шаг 2
Нарисуйте круг с центром в точке пересечения вспомогательных линий. Стоит сказать, что октаэдр является геометрической фигурой, которую можно вписать в шар таким образом, что каждая вершина октаэдра будет иметь общую точку с поверхностью шара. Но так как мы рисуем октаэдр в двумерном пространстве, мы нарисуем круг.
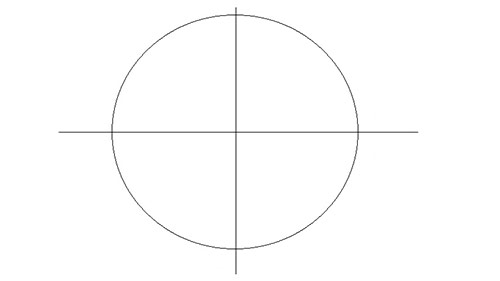
Шаг 3
Нарисуйте эллипс. Если представить его в трёхмерном виде, то это будет горизонтальная плоскость разделяющая шар на две равных полусферы.
Существует несколько способов определить площадь поверхности октаэдра. Он представляет собой один из пяти правильных многоугольников или так называемых Платоновых тел. Имеет восемь одинаковых граней (поверхностей) в виде равносторонних треугольников, к каждой из его вершин прилагается по четыре грани. Рассмотрим, что собой представляет тело, где встречается в природе, как вычисляется его площадь и объём.
Что такое октаэдр
- 6 вершин, из которых выходит по 4 грани;
- 12 рёбер;
- 8 поверхностей.

Свойства октаэдра
- Вписывается в тетраэдр, при этом:
- 4 из 8 граней совмещаются с поверхностями тетраэдра;
- 6 вершин совмещается с центрами рёбер тетраэдра.
- Октаэдр вписывается в куб, при этом все его вершины располагаются в центре граней куба.

- В тело вписывается куб, вершины которого находятся в центрах граней куба.

- Симметрия куба и вписанного (описанного) октаэдра совпадают.
- Двойственен кубу.
- Является полным усечением тетраэдра.
- Имеет равные ребра и диагонали.
- Состоит из равносторонних треугольников.
- Диагонали тела взаимоперпендикулярны, в точке пересечения делятся на равные отрезки.
- Октаэдр симметричен, причём 3 оси пролегают через противоположные вершины, 6 – через центры ребер.
- Центр симметрии тела расположен в точке пересечения диагоналей.
- Ребра равны по длине, поверхности – по площади.
Математические характеристики тела
Как вычислить площадь поверхности октаэдра
Площадь октаэдра равна сумме площадей составляющих его треугольников:
Здесь Sтреуг – площадь треугольника.
После подстановки значения получится требуемый результат.
Если известна длина ребра, придётся вычислить площадь треугольников.
Подставляем значение в первое выражение:
Упрощаем: после сокращения дроби на четыре получается формула площади поверхности октаэдра:
2. S = 8 * Sтреуг = 2 \sqrt a^2.
Существует ещё один способ проведения вычислений. Он менее точный чем предыдущие, однако позволяет обойтись без калькулятора. При приблизительном подсчёте 2 \sqrt равняется 3,464 или 3,46.
3. S = 3,464 a^2.
Здесь a – длина стороны треугольника (равны).
Для примера, имеется фигура октаэдр с длиной стороны 5 см.
S=2\sqrt a^2=2*\sqrt *5^2=2*\sqrt *25=50\sqrt \approx 86,6 см.
Как вычислить объём правильного октаэдра
Объём показывает размер внутреннего пространства геометрического тела. Объем правильного октаэдра вычисляется, если знаете длину ребра геометрического тела, по формуле:
После проведения приблизительных расчётов \frac \approx 0,47 формула принимает следующий вид :
Рассчитаем двумя методами на примере правильного многоугольника с гранью, равной 5 см:
V= 0,47 * a^3 = 0,47*125 \approx 58,93
Значения совпали, во втором случае нужно выполнять гораздо меньше операций. Подходит он только, если не требуется исключительная точность – при округлении до 4-5 знаков после запятой точность снизится.
Развёртка
Октаэдр, как большинство гомерических тел, имеет развёртку поверхности – это плоская фигура, полученная путём совмещения поверхности модели с одной плоскостью без пересечения либо наложения граней друг на друга.
Рисунок развёртки октаэдра.

В природе насчитывается 11 разновидностей развёртки октаэдра, позволяющих создать его модель из бумаги или картона. Наиболее распространённая выглядит как восемь одинаковых треугольников. Шесть из них размещено в ряд, к третьему и четвёртому основаниям прилегает ещё по одному, их вершины направлены в противоположные стороны.
Октаэдр в природе
Октаэдр — один из 5-ти выпуклых правильных многогранников - Платоновых тел.
У октаэдра 8 треугольных граней, 12 рёбер, 6 вершин, к каждой его вершине сходятся 4 ребра.
На примере октаэдра легко проверить формулу Эйлера 6в+8г-12р=2. В каждой из вершин октаэдра сходятся 4 треугольника, т.о., сумма плоских углов у вершины октаэдра равна 240°. Из понятия правильного многогранника делаем вывод, что каждое ребра октаэдра имеет одинаковую длину, а грань - одинаковую площадь.
Обозначим длину ребра октаэдра как а, значит площадь полной поверхности октаэдра (S) и объём октаэдра (V) найдем из таких формул:


Радиус описанной сферы около октаэдра:

Радиус вписанной сферы около октаэдра:
Сумма длин всех ребер равна 24а.

Двугранный угол: α=2ϕ≈109,47°, где .
Свойства октаэдра.
Октаэдр легко вписывается в куб (гексаэдр), при этом каждая из 6-ти вершин октаэдра совместится с центрами 6-ти граней куба.
У правильного октаэдра есть симметрия Oh, которая совпадает с симметрией куба.
Развёртка октаэдра.

Симметрия октаэдра.
3 из девяти осей симметрии октаэдра проходят сквозь противолежащие
вершины, 6 - квозь середины ребер.
Центр симметрии октаэдра - точка пересечения осей симметрии октаэдра.
3 из девяти плоскостей симметрии тетраэдра проходят сквозь все 4 вершины октаэдра, которые лежат в одной плоскости.
6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.
Читайте также:


