Как сделать округление в маткаде
Основная нагрузка, если можно так выразиться, в процессе решения практически любой задачи ложится на ядро из стандартных математических функций, которые приведены и кратко описаны в табл. 22.2 .
Арккосинус от z
Гиперболический арккосинус от z
Арккотангенс от z
Гиперболический арккотангенс от z
Арккосеканс от z
Гиперболический арккосеканс от z
Гиперболический арксеканс от z
Гиперболический арксинус от z
Арктангенс от z
Функцией в качестве результата возвращается угол (в радианах) между
осью Ох и прямой, проходящей через начало координат иточку с коор-
динатами х и у. Другими словами, atan2(x,y) = atan(y/x)
Гиперболический арктангенс от z
Гиперболический косинус от z
Гиперболический котангенс от z
Гиперболический косеканс от z
Показательная функция ( е ≈ 2.72 в степени z)
Гамма-функция Эйлера от z. Вычисляется как Г(z) = ∞ ∫ t z − 1 exp( − t ) dt
Логарифм натуральный от z
Логарифм натуральный от гамма-функции Эйлера с аргументом z.
Символ Г можно ввести так: сначала ввести большую литеру G (ком-
бинация клавиш + ), после чего нажать комбинацию клавиш
Математическое программное обеспечение. Учебное пособие
22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.11. Стандартные математические функции
Окончание табл. 22.2
Логарифм от z по основанию b, если второй аргумент функции не ука-
зан, логарифм вычисляется по основанию 10
Функция, значение которой вычисляется по формуле sinc(z) = sin(z)/z
Синус гиперболический от z
Тангенс гиперболический от z
Примеры вызова некоторых функций см. на рис. 22.14 .
В рабочих документах MathCad допустимы не только действительные числа, но и комплексные. Они могут быть, в частности, аргументом (или аргументами) для большинства стандартных математических функций. Кроме того, в MathCad есть функции, предназначенные для работы именно с комплексными числами, причем в некоторых случаях возвращаемое функцией значение, в силу ее определения в MathCad, несколько отличается от того, которое можно было бы ожидать исходя из общематематических представлений. Например, функцией signum( ) в качестве значения возвращается в общем случае комплексное число, равное отношению числа-аргумента функции к модулю этого аргумента. Если аргумент у функции нулевой, функцией возвращается значение 1. Таким образом, для действительного аргумента функция возвращает его знак. В некотором родстве к ней (если так можно
Математическое программное обеспечение. Учебное пособие
22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.12. Математические функции
сказать о функции) находится функция csgn ( ). Однако возвращаемое этой функцией значение всегда действительно. Алгоритм его вычисления довольно замысловат. Функцией возвращается знак действительной части аргумента. Если число мнимое (т. е. действительная часть равна нулю), функция возвращает знак мнимой части аргумента. Для нулевого аргумента значение функции равно нулю. Поэтому для действительных аргументов различие функций signum( ) и csgn( ) состоит лишь в том, что первая для нуля возвр а- щает значение 1, а вторая – 0.
Функции вычисления действительной и мнимой частей комплексного числа в MathCad имеют общепринятые математические названия: Re ( ) для вычисления действительной части и Im( ) – для мнимой. Наконец, аргумент комплексного числа (это угол между действительной осью и вектором, направленным из начала системы координат к точке на комплексной плоскости) можно определить с помощью функции arg ( ) . Здесь уместно напомнить, что для задания комплексного числа достаточно знать два параметра. Это могут быть действительная и мнимая части комплексного числа либо его модуль и аргумент. Модуль комплексного числа можно вычислить, заключив число в прямые скобки.
22.13. Работа с комплексными числами
Пример функций с комплексными аргументами см. на рис. 22.15 .
22.14. Функции округления численных значений
Группа функций MathCAD, предназначенная для преобразования и округления численных значений, приведена в табл. 22.3 . Эти функции собраны в категории Truncation and Round Off диалогового окна вставки функций
Математическое программное обеспечение. Учебное пособие
22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.14. Функции округления численных значений
Функцией в качестве значения возвращается наименьшее
кратное числа у, не меньшее числа х
Функцией возвращается наименьшее целое число, которое
больше либо равно х
Возвращается наибольшее кратное у, не превышающее х
Значением функции является наибольшее возможное целое
число, не превышающее х
Значение х округляется до ближайшего числа, кратного вто-
рому аргументу функции у. Это значение и возвращается
функцией, при этом значение переменной х не меняется
Число х округляется до n знаков после десятичной точки. Если
второй аргумент функции не указан, то округление выполня-
ется до целочисленного значения. При отрицательном значе-
нии n абсолютное значение второго аргумента определяет ко-
личество разрядов округления в целой части числа
Функцией в качестве значения возвращается результат умно-
жения второго аргумента функции (т. е. у) на целую часть от-
ношения первого аргумента (т. е. х) ко второму
Функцией возвращается целая часть числа х
22.15. Символьный результат
При попытке вычислить значение функции в символьном виде, т. е. когда аргументами указаны не числа, а символы (названия переменных, которым не присвоены численные значения) с помощью ввода знака равенства после названия функции, результат будет негативным. Однако сделать это можно, если вместо знака равенства ввести оператор вычисления символьного значения (стрелка вправо). Причем в качестве аргументов можно указывать не только отдельные названия, но и целые выражения.
Инструкция
Что вам понадобится:
1 шаг
Щелкнуть по результату левой кнопкой мышки. Появится синий уголок.
2 шаг
3 шаг
4 шаг
5 шаг
Если нужно изменить формат вывода сразу всех результатов в одном маткадовском документе – выделите левой кнопкой мышки несколько результатов (вокруг них появятся прямоугольники из черных штриховых линий). Далее последовательность действий такая же, как и при форматировании только одного результата.
Ваш комментарий
Запросить инструкцию
Не нашли нужную пошаговую инструкцию?
Возможно, что кто-то из посетителей сайта сможет помочь. Оставьте запрос прямо сейчас, если Вы уверены, что эта тема ещё не освещена на нашем проекте!
Пример 1. Составить программу для вычисления корней квадратного уравнения: ax 2 + bx + c = 0 по известной формуле:
Алгоритм (1) является линейным и фрагмент документа MathCAD содержит конструкции, приведенные на рис 1.
П рограммирование разветвляющихся алгоритмов
Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких возможных ветвей вычислений. Выбор конкретной ветви зависит от выполнения (или не выполнения) заданных условий на значения переменных алгоритма.
Пример 2. Значение переменной y зависит от значений переменной x и определяется выражением:
Для реализации разветвляющегося алгоритма необходимо использовать:
· конструкции, проверяющие выполнение заданных условий;
· конструкции, выбирающие нужную ветвь вычислений в зависимости от результатов проверки заданных условий.
Для проверки заданных условий в MathCAD используется: выражение отношений, логические операции и логические выражения.
Выражением отношений (или просто отношением) называется конструкция вида:
где , - произвольные арифметические выражения, - любая из следующих операций: (здесь вертикальные чёрточки являются разделительным символом при перечислении).
Для ввода знаков операций отношений можно использовать палитру Булево (приведённую на рис.3) или использовать клавиши, обозначения которых приведены в таб. 1.

Палитра инструментов БУЛЕВО
Внимание! Не следует путать знак операции сравнения = с похожим знаком вывода значений переменных. Знак операции = имеет больший размер и более жирное начертание.
Выражение отношений принимает одно из двух значений: 1 - если заданное отношение выполняется или 0 – в противном случае. Значение 1 можно интегрировать как значение истина, а 0 – как ложь .
Задание 1 . Пусть значения целой переменной x =3 . Определить значение следующих выражений отношений:
Для проверки более сложных условий используются четыре логических операций, обозначение которых приведены в табл. 2
Таблица 2
Логическое отрицание ( NOT )
Логическое ИЛИ ( OR )
Логическое И ( AND )
Исключающее ИЛИ ( XOR )
Знаки этих операций вводится с палитры Булево . Результат выполнения этих операций, приведен в табл. 3.
Логическим выражением называется конструкция, состоящая из выражений отношений, логических операций и круглых скобок. Логическое выражение принимает только одно из двух значений: 1 или 0; вычисляется слева направо с учетом приоритета входящих в выражение операции. Наивысший приоритет круглые скобки, а затем по убыванию: AND , OR и XOR – одинаковый приоритет и самый низкий приоритет выражения отношений.
Задание 2 . Определите порядок вычисления значений логических выражений в документе MathCAD , приведенных на рисунке 3
Рис. 3 Примеры логических выражений
Пример 2. Записать логическое выражение, принимающее значение 1 при попадании точки с координатами ( x , y ) в первую четверть.
Логическое выражение имеет вид
Для выбора нужной ветви разветвляющегося алгоритма используется конструкция, названная условной функцией if , записывается в виде:
if ( , , ),
где имя функции if вводится с клавиатуры.
Если логическое выражение равно 1, то значение функции определяется выр.1, в противном случае – выр. 2. Блок-схема этой функции приведена на рис. 4.
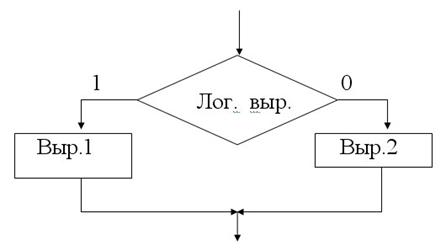
Рис. 4. Блок-схема функции if
При программировании разветвляющихся алгоритмов с тремя и более вычислительных ветвей на месте выр. 1 и выр. 2 вновь может использоваться функция if .
Пример 3. Используя условную функцию if запрограммировать два разветвляющихся алгоритма:
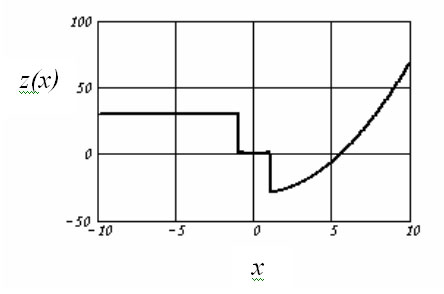
Рис. 5. Реализация разветвляющихся алгоритмов
В MathCAD имеется ряд встроенных функций, которые возвращают результат, зависящий от знака или величины аргумента и которые могут использоваться при программировании разветвляющихся алгоритмов. Приведем некоторые из них:
· ceil ( x ) – наименьшее целое, большее или равное x ;
· trunc ( x ) – целая часть вещественного числа x ;
· floor ( x ) – наибольшее целое, меньшее или равное x ;
· round ( x , n ) – округленное значение вещественного x с точностью до n знаков после десятичной точки;
· Ф( x ) – функция Хевисайда – равна 0 при x и 1 в противном случае;
· sign ( x ) – функция знака (равна 0 если x = 0; -1, если x и 1 , если x >0 );
· signum ( x ) – возвращает 1, если x = 0 и в остальных случаях.
Программирование циклических алгоритмов
Типы циклов. П о способам организации цикла можно выделить:
а) цикл типа арифметической прогрессии;
б) итерационный цикл.
Программирование цикла типа арифметической прогрессии
Особенностью цикла типа арифметической прогрессии является изменение параметра цикла по закону арифметической прогрессии и поэтому можно, не выполняя цикла, определить количество повторений цикла.
Параметр такого цикла задается дискретной переменной и тогда конструкции, входящие в тело цикла располагаются, начиная от этого описания и до конца документа MathCAD или до конструкции, переопределяющей дискретную переменную – параметр цикла.
Этот цикл имеет уже два параметра: i – параметр, определяющий номер строки; j – параметр, определяющий номер столбца матрицы. Заметим, что такой цикл называется двойным циклом.
Заметим, что если параметр цикла не входит в индексные выражения элементов массива, то он может принимать вещественные значения.
Заметим, что во фрагментах, приведенных на рисунках системная переменная ORIGIN =1.
Основная нагрузка, если можно так выразиться, в процессе решения практически любой задачи ложится на ядро из стандартных математических функций, которые приведены и кратко описаны в табл. 22.2 .
Арккосинус от z
Гиперболический арккосинус от z
Арккотангенс от z
Гиперболический арккотангенс от z
Арккосеканс от z
Гиперболический арккосеканс от z
Гиперболический арксеканс от z
Гиперболический арксинус от z
Арктангенс от z
Функцией в качестве результата возвращается угол (в радианах) между
осью Ох и прямой, проходящей через начало координат иточку с коор-
динатами х и у. Другими словами, atan2(x,y) = atan(y/x)
Гиперболический арктангенс от z
Гиперболический косинус от z
Гиперболический котангенс от z
Гиперболический косеканс от z
Показательная функция ( е ≈ 2.72 в степени z)
Гамма-функция Эйлера от z. Вычисляется как Г(z) = ∞ ∫ t z − 1 exp( − t ) dt
Логарифм натуральный от z
Логарифм натуральный от гамма-функции Эйлера с аргументом z.
Символ Г можно ввести так: сначала ввести большую литеру G (ком-
бинация клавиш + ), после чего нажать комбинацию клавиш
Математическое программное обеспечение. Учебное пособие
22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.11. Стандартные математические функции
Окончание табл. 22.2
Логарифм от z по основанию b, если второй аргумент функции не ука-
зан, логарифм вычисляется по основанию 10
Функция, значение которой вычисляется по формуле sinc(z) = sin(z)/z
Синус гиперболический от z
Тангенс гиперболический от z
Примеры вызова некоторых функций см. на рис. 22.14 .
В рабочих документах MathCad допустимы не только действительные числа, но и комплексные. Они могут быть, в частности, аргументом (или аргументами) для большинства стандартных математических функций. Кроме того, в MathCad есть функции, предназначенные для работы именно с комплексными числами, причем в некоторых случаях возвращаемое функцией значение, в силу ее определения в MathCad, несколько отличается от того, которое можно было бы ожидать исходя из общематематических представлений. Например, функцией signum( ) в качестве значения возвращается в общем случае комплексное число, равное отношению числа-аргумента функции к модулю этого аргумента. Если аргумент у функции нулевой, функцией возвращается значение 1. Таким образом, для действительного аргумента функция возвращает его знак. В некотором родстве к ней (если так можно
Математическое программное обеспечение. Учебное пособие
22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.12. Математические функции
сказать о функции) находится функция csgn ( ). Однако возвращаемое этой функцией значение всегда действительно. Алгоритм его вычисления довольно замысловат. Функцией возвращается знак действительной части аргумента. Если число мнимое (т. е. действительная часть равна нулю), функция возвращает знак мнимой части аргумента. Для нулевого аргумента значение функции равно нулю. Поэтому для действительных аргументов различие функций signum( ) и csgn( ) состоит лишь в том, что первая для нуля возвр а- щает значение 1, а вторая – 0.
Функции вычисления действительной и мнимой частей комплексного числа в MathCad имеют общепринятые математические названия: Re ( ) для вычисления действительной части и Im( ) – для мнимой. Наконец, аргумент комплексного числа (это угол между действительной осью и вектором, направленным из начала системы координат к точке на комплексной плоскости) можно определить с помощью функции arg ( ) . Здесь уместно напомнить, что для задания комплексного числа достаточно знать два параметра. Это могут быть действительная и мнимая части комплексного числа либо его модуль и аргумент. Модуль комплексного числа можно вычислить, заключив число в прямые скобки.
22.13. Работа с комплексными числами
Пример функций с комплексными аргументами см. на рис. 22.15 .
22.14. Функции округления численных значений
Группа функций MathCAD, предназначенная для преобразования и округления численных значений, приведена в табл. 22.3 . Эти функции собраны в категории Truncation and Round Off диалогового окна вставки функций
Математическое программное обеспечение. Учебное пособие
22. ПЕРЕМЕННЫЕ И ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ОПЕРАЦИИ В MATHCAD
22.14. Функции округления численных значений
Функцией в качестве значения возвращается наименьшее
кратное числа у, не меньшее числа х
Функцией возвращается наименьшее целое число, которое
больше либо равно х
Возвращается наибольшее кратное у, не превышающее х
Значением функции является наибольшее возможное целое
число, не превышающее х
Значение х округляется до ближайшего числа, кратного вто-
рому аргументу функции у. Это значение и возвращается
функцией, при этом значение переменной х не меняется
Число х округляется до n знаков после десятичной точки. Если
второй аргумент функции не указан, то округление выполня-
ется до целочисленного значения. При отрицательном значе-
нии n абсолютное значение второго аргумента определяет ко-
личество разрядов округления в целой части числа
Функцией в качестве значения возвращается результат умно-
жения второго аргумента функции (т. е. у) на целую часть от-
ношения первого аргумента (т. е. х) ко второму
Функцией возвращается целая часть числа х
22.15. Символьный результат
При попытке вычислить значение функции в символьном виде, т. е. когда аргументами указаны не числа, а символы (названия переменных, которым не присвоены численные значения) с помощью ввода знака равенства после названия функции, результат будет негативным. Однако сделать это можно, если вместо знака равенства ввести оператор вычисления символьного значения (стрелка вправо). Причем в качестве аргументов можно указывать не только отдельные названия, но и целые выражения.
Читайте также:








