Как сделать одинаковый знаменатель у дробей с буквами
Вспомним, что общий знаменатель дробей делиться на знаменатели данных нам дробей. Чтобы сравнить дроби с разными знаменателями, нужно привести их к общему знаменателю, а потом сравнивать числители. Из двух дробей с одинаковыми знаменателями больше будет та дробь, числитель которой больше.
Нам даны две дроби 1/2 и 4/5. Выберем больший знаменатель и проверим, будет ли он делиться на меньший знаменатель: 5 на 2 не делится. Умножим больший знаменатель на 2 и посмотрим, делится ли новое число на меньший знаменатель: 5 × 2 = 10.
10 делится на 2. Значит меньший общий знаменатель этих дробей равен 10.
Чтобы в знаменатели дроби 1/2 появилось число 10, умножим и числитель и знаменатель на 5:
1/2 = (1 × 5) / (2 × 5) = 5/10.
Чтобы в знаменатели дроби 4/5 появилось число 10, умножим и числитель и знаменатель на 2:
Для нахождения разницы 2х дробей с одинаковыми знаменателями, необходимо вычесть из числителя 1й дроби числитель 2й дроби, а знаменатель обоих дробей оставить не изменяя. Вычитание обыкновенных дробей:

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь, которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной, единицу переводят к виду неправильной дроби, у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7, т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.
Правила вычитания дробей – правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби – выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей.
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ), и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители, то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители; все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:

Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Дробь — это доля числа. Она представлена в виде \frac mn, где m и n — любые натуральные числа. В данной записи m является числителем, а n — знаменателем.
Для того чтобы производить операции с дробями, необходимо знать их основное свойство. Оно состоит в следующем: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Одно и то же количество можно выразить разными эквивалентными дробями.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если числитель и знаменатель дроби \(\frac12\) умножить на 2, получится равная ей дробь \(\frac24.\)
Основные правила, операции без преобразования
Сложение (вычитание) дробей — это упрощение выражений вида \(\frac ab\pm\frac cb\) или \(\frac ab\pm\frac cd\) , где \(c\neq d.\)
Главное правило сложения и вычитания дробей заключается в том, что операции можно проводить только между дробями с одинаковым знаменателем.
Если знаменатели двух дробей одинаковы, то можно сразу сложить или вычесть, в зависимости от задачи, числители этих дробей, а знаменатель оставить прежним. Если это возможно, дробь нужно сократить.
Общее правило сложения и вычитания дробей с одинаковым знаменателем выглядит следующим образом:
где a, b и с — натуральные числа, \(b\neq0.\)
Если знаменатели разные, дроби необходимо заменить на эквивалентные с одинаковым знаменателем. Выполнить операцию необходимо уже с этими новыми дробями. Распространяется это как на положительные, так и на отрицательные дроби.
Сложение и вычитание алгебраических дробей
Приведение алгебраических дробей к общему знаменателю
Для каждой дроби существует бесконечное количество эквивалентных дробей. Это значит, что обязательно есть знаменатель, являющийся одинаковым для двух или более дробей, с которыми производится действие. Такой знаменатель называют общим.
Чтобы упростить вычисления, обычно используют метод наименьшего общего кратного.
Наименьшее общее кратное (НОК) — это такое наименьшее натуральное число, которое делится одновременно на оба числа. В данном случае это числа, стоящие в знаменателях двух дробей.
Для чисел 2 и 3 произведение и НОК = 6; для чисел 5 и 10 произведение равно 50, а НОК = 10; произведение чисел 4 и 6 равно 24, а их НОК = 12.
Как видно из последних двух примеров, НОК зачастую меньше, чем производное двух данных чисел. Благодаря НОК можно значительно сократить запись решения, поскольку отпадает нужда в ненужном сокращении дробей.
Чтобы найти НОК, необходимо разложить знаменатели обеих дробей на простые множители, а затем выбрать в разложении наименьшего знаменателя множители, не вошедшие в разложение большего знаменателя, и добавить их туда. После чего перемножить все полученные множители.
Найдем НОК чисел 12 и 18.
В разложение наименьшего знаменателя 12 вошли множители 3, 2 и 2. А в разложении наибольшего знаменателя 18 множитель 2 встречается только один раз, в нем не хватает еще одного множителя 2. Поэтому мы добавляем его к множителям числа 18. Получаем:
Чтобы привести дроби к общему знаменателю, необходимо найти не только НОК, но и дополнительный множитель. Это такой множитель, на который необходимо умножить каждую из дробей. Для этого необходимо поделить НОК на знаменатель каждой дроби.
Найдем дополнительный множитель для дробей \(\frac1\) и \(\frac5.\)
НОК для этих дробей уже известно и равно 36. Тогда:
Следовательно, дополнительный множитель для первой дроби равен 3, а для второй – 2.
Затем каждую дробь необходимо умножить на дополнительный множитель и произвести действия с полученными дробями с одинаковыми знаменателями.
Найдем значения выражений \( \frac1+\frac5\) и \(\frac5-\frac1.\)
Таким образом, можно сформулировать алгоритм сложения и вычитания алгебраических дробей с разными знаменателями.
- Найти наименьшее общее кратное знаменателей дробей.
- Найти дополнительный множитель для каждой дроби.
- Умножить изначальные дроби на дополнительный множитель, чтобы привести их к общему знаменателю, преобразовав в эквивалентные дроби.
- Провести операцию сложения или вычитания между числителями, а знаменатель оставить неизменным. При возможности дробь сократить.
С помощью формул сокращенного умножения
Иногда в знаменателе находится не простое число, а выражение, так что найти НОК не удается. В таких случаях стоит присмотреться к выражению в знаменателе: возможно, там будет формула сокращенного умножения. К таким формулам относят:
- квадрат суммы: \(^2=a^2+2ab+b^2\)
- квадрат разности: \(^2=a^2-2ab+b^2\)
- разность квадратов: \(a^2-b^2=(a-b)(a+b)\)
- куб суммы: \(^3=a^3+3a^2b+3ab^2+b^3\)
- куб разности: \(^3=a^3-3a^2b+3ab^2-b^3\)
- сумма кубов: \(a^3+b^3=(a+b)(a^2-ab+b^2)\)
- разность кубов: \(a^3-b^3=(a-b)(a^2+ab+b^2)\)
С вынесением общего множителя за скобки
При нахождении общего знаменателя может понадобиться разложить исходный сложный знаменатель на множители, чтобы упростить его.
С одночленом или числом
Если необходимо сложить (вычесть) дробь и натуральное число, необходимо представить это число в виде дроби с тем же знаменателем. Результатом вычисления может получиться неправильная дробь — в таком случае необходимо преобразовать ее в смешанное число.
Если число не целое, а смешанное, то работать нужно отдельно с целыми и дробными частями.
В случае с одночленами, то есть выражениями с одной переменной, действия производятся так же, как и с целыми числами. Одночлен необходимо представить в виде дроби.
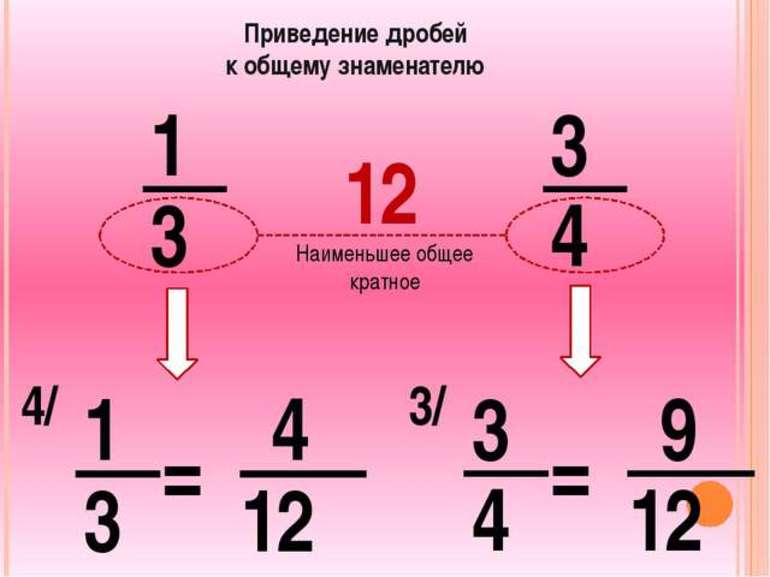
Одна из важных тем в математике, которую проходят в 5 классе, — приведение дробей к общему знаменателю. Обыкновенные дроби состоят из двух частей — числителя (верхней) и знаменателя (нижней). Знаменатели в дробях может быть одинаковым — это и называется общий, а могут быть разными, и в таком случае их можно привести к общему с помощью определенных действий.

Общий знаменатель
Самый простой способ, как привести дробь к общему знаменателю, — верхнюю и нижнюю части первой дроби умножить на значение в знаменателе второй, а верхнюю и нижнюю часть второго дробного числа — на значение в знаменателе первой. Проверочное правило, действующее в этом случае: дробь не меняется, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Даны две дроби: 3/13 и 3/7. После выполнения необходимых действий получится: 3/13*7 = 21/91, 3/7*13 =39/91.
Общий знаменатель (ОЗ) — это любое натуральное число, которое является всеобщим кратным всех данных дробей. Иными словами, это значит, что ОЗ может быть любое число из натуральных, которое обязательно будет делиться на знаменатель каждого дробного числа. Допустим, есть две обычных дробных соотношения 4/8 и 5/10. ОЗ в этом случае может быть любым значением, кратным 8 и 10. А конкретно, это значения: 80, 160, 240, 320, 400 и так далее.
Дано 3 дробных значения: 1/5, 3/10 и 9/15. Вопрос: может ли ОЗ быть числом 330? Ответ: да, потому что оно делится на знаменатель каждого соотношения без остатка: 330/5 = 66, 330/10 = 33, 330/15 = 22.
НОЗ и НОК
При работе с дробями используются наименьший общий знаменатель (НОЗ) — это наименьшее натуральное число среди всех ОЗ ряда дробных чисел и наименьшее общее кратное (НОК) — это самый меньший общий делитель данного ряда чисел.
Наименьшее общее кратное — это НОЗ этого ряда. К нему можно прийти поиском НОК.
Например, необходимо провести следующую операцию для двух дробных значений: 7/16, 19/6. Нужно узнать, какой НОК у 16 и 6. Простые множители этих чисел:
НОК (16, 6) =8*2*3= 48.
Число 48 и есть искомый НОЗ.

Существует простое правило о том, как перевести дробное число к НОЗ. Вычисления проводятся по порядку:
- Найти НОК.
- Для каждого дробного числа из ряда определить дополнительный множитель. Определить его можно с помощью деления НОЗ на знаменатель каждой из дробей.
- Умножить обе части каждой дроби на их дополнительные множители.
Пример. Есть 2 дробных значения: 3/14 и 18/30. Теперь можно воспользоваться правилом, для того чтобы найти НОЗ:
- Найти НОК: 14 = 2*7; 30 = 5*2*3; НОК (14,32) = 5*2*7*3 = 210;
- Найти дополнительные множители: 210/14 = 15; 210/30 = 7;
- Перемножить верхнюю и нижнюю части с дополнительными множителями: 3*15/14*15 = 45/210; 18*7/30*7 = 126/210.
Примеры с несколькими дробями
Правило поиска ОЗ и НОЗ действует также и в отношении нескольких дробных чисел в ряде. Есть три значения: 3/9, 8/11 и 10/12. Для того чтобы переводить их, нужно совершать те же действия, которые представлены в правиле:
НОК (9; 11) = 99; НОК (99; 12) = 39; НОК (9; 11; 12) = 396;
396/9 = 44; 396/11 = 36; 396/12 = 33;
3*44/9*44 = 132/396; 8*36/11*36 =288/396; 10*33/12*33 =330/396;
Приводить дробные соотношения к ОЗ требуется во многих случаях. Вычисление этой величины необходимо, чтобы получить разность дробей, провести их сложение, умножение или деление, а также при решении задач на доли и проценты, так как процентные соотношения — это обыкновенные выражения, которые содержат дробные соотношения.
Читайте также:


