Как сделать обратную пропорциональность
1) - периметр квадрата, - его сторона.
= 4.
Если = 1 см, то = 41 = 4 (см).
Если = 2 см, то = 42 = 8 (см).
Если = 4 см, то = 44 = 16 (см).
Получаем, что каждый раз, увеличивая сторону квадрата в 2 раза, его периметр также будет увеличиваться в 2 раза. Аналогично, если сторону квадрата будем уменьшать в какое-то число раз, то и периметр квадрата будет уменьшаться в это же число раз. Следовательно, величины и прямо пропорциональны. Можно сказать еще и так: "величина прямо пропорциональна величине " или "зависимость между величинами и является прямой пропорциональностью".
2) При движении с постоянной скоростью, пройденный путь и время движения прямо пропорциональны, т.к. пройденный путь равен произведению скорости и времени движения.
Пусть скорость движения пешехода 8 км/ч.
Если = 1 ч, то = 81 = 8 (км).
Если = 3 ч, то = 83 = 24 (км).
Если = 9 ч, то = 89 = 72 (км).
Получаем, что каждый раз, увеличивая время в пути в 3 раза, путь также будет увеличиваться в 3 раза, а это и говорит о том, что зависимость между величинами и является прямой пропорциональностью, при условии движения с постоянной скоростью.
Свойство прямо пропорциональных величин:
| Если две величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу. |
В рассмотренных выше примерах для величин и это число равно 4, т.к. : = 4 : 1 = 8 : 2 = 16 : 4 = 4, а для величин и это число равно 8, т.к. : = 8 : 1 = 24 : 3 = 72 : 9 = 8.
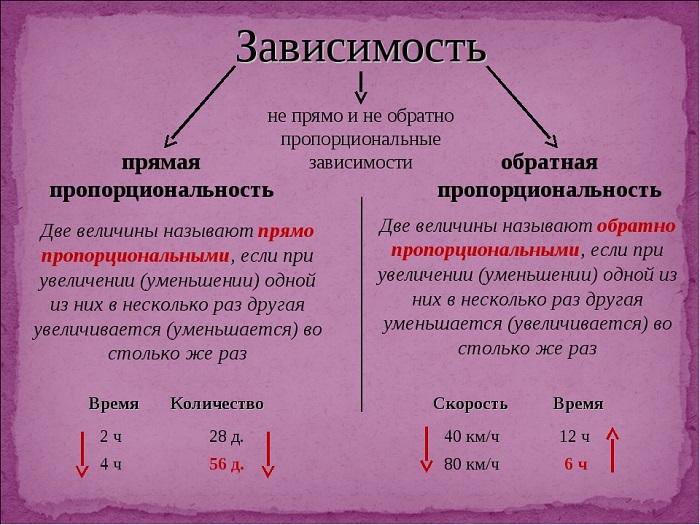
Обратная пропорциональная зависимость
| Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. |
Примеры:
1) Если расстояние является постоянной величиной, то скорость и время движения обратно пропорциональны, т.к. время движения равно частному от деления расстояния на скорость движения.
Пусть расстояние равно 80 км.
Если = 10 км/ч, то = 80 : 10 = 8 (ч).
Если = 20 км/ч, то = 80 : 20 = 4 (ч).
Если = 40 км/ч, то = 80 : 40 = 2 (ч).
Получаем, что каждый раз, увеличивая скорость движения в 2 раза, время движения будет уменьшаться в 2 раза, а это и говорит о том, что зависимость между величинами и является обратной пропорциональностью, при том условии, что расстояние нужно проехать одинаковое.
2) и - стороны прямоугольника, а его площадь 36 см 2 .
Если = 3 см, то = 36 : 3 = 12 (см).
Если = 6 см, то = 36 : 6 = 6 (см).
Получаем, что величины и обратно пропорциональны, т.к. увеличивая (уменьшая) одну сторону прямоугольника в 2 раза, чтобы его площадь не изменилась, вторую сторону нужно уменьшить (увеличить) в 2 раза.
Свойство обратно пропорциональных величин:
| Если две величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу. |
В рассмотренных выше примерах для величин и это число равно 80, т.к. = 108 = 204 = 402 = 80, а для величин и это число равно 12, т.к. = 312 = 66 = 36.
Не всякие величины являются прямо пропорциональными или обратно пропорциональными. Например, размер обуви человека увеличивается при увеличении его возраста, но эти величины не являются пропорциональными, т.к. при удвоении возраста размер обуви человека не удваивается.
Пусть нам дана задача:
Украшение состоит из белого и желтого золота массой 192 г. При этом масса белого золота относится к массе желтого золота как 5 : 7. Надо найти массу белого и желтого золота, из которых сделано украшение.
Мы можем считать, что все украшение состоит из 5 + 7 = 12 частей одинаковой массы. По условию масса украшения равна 192 г, а значит, масса одной части украшения равна 192 : 12 = 16 г.
Белое золото соответствует 5 частям, то есть имеет массу 5 16 = 80 г, а желтое золото соответствует 7 частям, то есть имеет массу 7 16 = 112 г.
Итак мы получили, что украшение состоит из 80 г белого золота и 112 г желтого золота.
То есть мы число 192 (масса украшения) представить в виде суммы двух слагаемых - 80 и 112, отношение которых равно 5 : 7.
В этом случае говорят, что число 192 разделили в отношении 5 : 7, или по-другому, число 192 представили в виде суммы двух слагаемых, пропорциональных числам 5 и 7.
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным. [1] . Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно, длина стороны квадрата зависит от его площади.
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина весят 1,6 кг, 5 л весят 4 кг, 7 л весят 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой [1] .
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
f(x) = ax,a = const
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
Математически обратная пропорциональность записывается в виде формулы:

Свойства функции:
См. также
Источники
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое "Обратная пропорциональность" в других словарях:
обратная пропорциональность — atvirkštinis proporcingumas statusas T sritis fizika atitikmenys: angl. inverse proportionality vok. umgekehrte Proportionalität, f rus. обратная пропорциональность, f pranc. proportionnalité inverse, f … Fizikos terminų žodynas
ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова
Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова
пропорциональность — и; ж. 1. к Пропорциональный (1 зн.); соразмерность. П. частей. П. телосложения. П. представительства в парламенте. 2. Матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент пропорциональности. Прямая п. (при которой с… … Энциклопедический словарь
пропорциональность — и; ж. 1) к пропорциональный 1); соразмерность. Пропорциона/льность частей. Пропорциона/льность телосложения. Пропорциона/льность представительства в парламенте. 2) матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент… … Словарь многих выражений
Прямая пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
МИКРОФОТОГРАФИЯ — МИКРОФОТОГРАФИЯ, получение при помощи светописи изображений микроскоп. объектов, обыкновенно наблюдаемых субъективно через окуляр микроскопа. Основные достоинствам., это точность и объективность даваемых ею изображений, сравнительная быстрота и… … Большая медицинская энциклопедия

Функцией прямой пропорциональности является частный случай линейной функции. Если линейная функция это y = k*x + b, то для прямой пропорциональности это выглядит так: y = k*x, гдеk называется коэффициентом пропорциональности, и это всегда не равно нулю число. Вычислитьk легко – он находится как частное функции и аргумента: k = у/х.
Чтобы было нагляднее, возьмем еще один пример. Представьте, что из пункта А в пункт Б движется автомобиль. Его скорость – 60 км/ч. Если предположить, что скорость движения остается постоянной, то ее можно принять за константу. И тогда запишем условия в виде: S = 60* t , и эта формула аналогична функции прямой пропорциональности y = k * x . Проведем параллель дальше: если k = у/х, то и скорость автомобиля можно вычислить, зная расстояние между А и Б и затраченное на дорогу время: V = S / t .
А теперь от прикладного применения знаний о прямой пропорциональности вернемся обратно к ее функции. К свойствам которой относится:
областью ее определения является множество всех действительных чисел (а также его подмножества);
изменение переменных прямо пропорционально осуществляется по всей длине числовой прямой.
Видео
Исследование функции прямой пропорциональности и ее график
Функция, которая обладает видом y = kx, где k — число (k≠0), является функцией прямой пропорциональности.
Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции
y = kx + m, если m=0
График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.
Прямая пропорциональность характеризуется следующими свойствами:
- областью определения является множество действительных чисел: D(y): x∈(-∞;+∞) (или x∈R);
- областью значений является множество действительных чисел: D(y): y∈(-∞;+∞) (или y∈R);
- нуль функции (y=0) при x=0;
- если k>0, функция y = kx возрастает, а при k 0, график функции пересекает первую и третью координатные четверти. Функция будет обладать положительными значениями, если значения аргумента положительные:
Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:
Если k 0 при x 0.
Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.
В качестве примера можно рассмотреть такие функции:
- y = 2x в виде прямой пропорциональности;
- y = 2x + 1 в виде линейной функции;
- y = 2x – 1 в виде линейной функции.
Можно построить график рассматриваемых функций. Каждая из них обладает коэффициентом k = 2. Для первой функции m = 0, для второй: m = 1, для третьей: m = -1. Данные величины вытекают из стандартной записи линейного уравнения:
Необходимо представить данные в виде таблицы:
График примет такой вид:
Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

a и d называются крайними членами, b и c — средними.
Основное свойство пропорции
Произведение крайних членов равно произведению средних членов.
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
- при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
- периметр квадрата и его сторона — прямо-пропорциональные величины;
- стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
- Вспомним формулу для определения пути через скорость и время: S = V * t.
- Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7
- Найдем скорость второго автомобиля: V = 70 * 2/7 = 20
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
- х = 1 (блогер) * 30 (раз) : 12/8 (дней).
- х = 1 * 30 : 12/8
- х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.

Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:

где k – любое действительное число, кроме 0.
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).

Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:

Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график

Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.

Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k 0;

Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:

Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
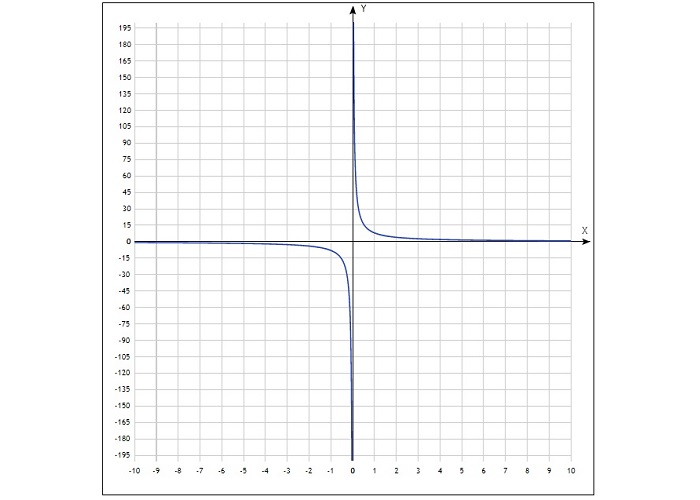
Свойства функции обратной пропорциональности

области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
оси координат 0х и 0у - это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Читайте также:


