Как сделать обратную матрицу

Обновлено: 24.01.2025

, главная диагональ - единицы, остальные элементы нули.

Если Δ ≠ 0 , то матрица называется невырожденной или неособенной; иначе, если равен нулю - вырожденной или особенной.

Теорема. Чтобы имела обратную матрицу, необходимо и достаточно, чтобы ее детерминант был отличен от нуля.

Для не квадратных и вырожденных обратных матриц не существует.

Обратная матрица для , обозначается через -1 , так что В = -1 вычисляется по формуле

где - алгебраические дополнения элементов a_ij , Δ = ||. Для не квадратной Δ, обратная матрица -1 не существуют.

Вычисление -1 по формуле (1) если имеет высокий порядок трудоёмко, поэтому удобнее найти обратную с помощью метода элементарных преобразований (ЭП). Любую неособенную путём ЭП только столбцов (или только строк) можно привести к единичной Е.

Если совершённые над ЭП в том же порядке применить к единичной Е, то результатом будет обратная матрица -1 . Проще совершать ЭП над и Е одновременно, записывая обе рядом через черту | E. Если нужно вычислить А -1 , то следует использовать только строки или только столбцы.

Свойства обратной матрицы

det(A -1 ) = 1/det(A), det обозначает определитель матрицы.
(AB) -1 = A -1 B -1 для двух квадратных обратимых A и B.
(A -1 ) T = (A T ) -1 ;
(kA) -1 = A -1 /k;
(A -1 ) -1 = A;
E -1 = E;
Решение системы линейных уравнений Ax = b (b - ненулевой вектор), x - искомый вектор, если A -1 существует, то x = A -1 b.

Вычисления обратной матрицы с помощью алгебраических дополнений

Алгоритм вычисления обратной А -1 :

Надо вычислить определитель |A|, если он не равен 0, то обратная А -1 существует.
Определяем * , матрица алгебраических дополнений _ij соответствующих элементов a_ij исходной матрицы . Сначала рассчитываем миноры M_ij - это определители, которые получаются вычёркиванием строки i и столбца j , _ij=(-1) i+j M_ij.
* = <> транспонируем - строки заменяем столбцами, *T - это союзная матрица (присоединённая, взаимная).
*T делим на |A|, обратная -1 = *T /Δ.

Пример_1. Дана 2×2 второго порядка, ? Найти обратную .

Найдём ||, он не равен 0, значит обратную -1 существует.
Вычислим алгебраические дополнения каждого элемента матрицы : для первой строки, , для второй строки , .
Составим , транспонируем её (строки заменяем столбцами) .
*T делим на Δ = -2. . Проверка

. Получена E, следовательно, обратная матрица

-1 вычислена верно.

Пример 2. Дана 3×3 третьего порядка, -1 ?.

Решение. det()?
он не равен 0, следовательно, обратная матрица -1 существует, ее можно вычислить по формуле: , где (i,j=1,2,3) - алгебраические дополнения элементов а_ij исходной . Вычислим их:

, * = , присоединённая *T = Искомая обратная матрица -1 = *T /Δ,

Вычисления обратной матрицы с помощью элементарных преобразований (метод Гаусса-Жордана)

Пример 3. Методом элементарных преобразований вычислить -1 если = .

Решение. Приписываем к исходной справа единичную того же порядка: . С помощью элементарных преобразований столбцов приведём левую “половину” к единичной, совершая одновременно точно такие преобразования над правой "половиной".
Поменяем местами 1 со 2 столбцы: ~. К третьему прибавим первый, ко второму - первый, × на -2: . Из первого вычтем удвоенный второй, из третьего - × на 6 второй; . Прибавим третий к первому и второму: . Умножим последний на минус один: . Справа от вертикальной черты квадратная таблица размером 3х3
.

Применение обратной матрицы

Решение систем линейных уравнений

Пример 4 Решить систему.

В матричной форме она примет вид: AX = B. Умножим это уравнение на -1 слева,

||== 2 + 2 -1 -1 + 4 -1 = 5. Так как он не равен 0, то - невырожденная, значит обратная -1 существует. Вычислим элементы * :

Составим , транспонируем её (строки заменяем столбцами) , делим ее на |A|= 5.

. Корни системы определим по формуле X = -1 B =

= x = =, исходная система решена x₁= 4, x₂= 2, x₃=1.

Обращение матрицы в Excel

Эта операция выполняется с помощью функции МОБР(). Сначала введем заполним ячейки A2:C4 исходные данные. Затем выделим ячейки под результат A7:C9 и нажмем комбинацию клавиш + + . В Excel всегда при матричных операций выделяется место под результат и вводится указанная комбинация клавиш.

В данной публикации мы рассмотрим, что такое обратная матрица, а также на практическом примере разберем, как ее можно найти с помощью специальной формулы и алгоритма последовательных действий.

Определение обратной матрицы

Для начала вспомним, что из себя представляют обратные значения в математике. Допустим, у нас есть число 7. Тогда обратное ему будет равняться 7 -1 или 1 /₇. Если умножить данные числа, в результате получится один, т.е. 7 · 7 -1 = 1.

Почти то же самое и с матрицами. Обратной называется такая матрица, умножив которую на исходную, мы получим единичную. Обозначается она как A -1 .

Алгоритм нахождения обратной матрицы

Для нахождения обратной матрицы нужно уметь вычислять определитель матрицы, а также иметь навыки выполнения определенных действий с ними.

Сразу отметить, что найти обратную можно только для квадратной матрицы, а делается это по формуле ниже:

| A | – определитель матрицы;
A T _M – транспонированная матрица алгебраических дополнений.

Примечание: если определитель равен нулю, то обратной матрицы не существует.

Пример
Давайте найдем для матрицы A ниже обратную ей.

Решение
1. Для начала найдем определитель заданной матрицы.

2. Теперь составим матрицу миноров, которая имеет те же самые размеры, что и исходная:

Нам нужно выяснить, какие числа должны стоять на месте звездочек. Начнем с верхнего левого элемента матрицы. Минор к нему находится путем зачеркивания строки и столбца, в котором он находится, т.е. в обоих случаях под номером один.

Число, которое останется после зачеркивания, и является требуемым минором, т.е. .

Аналогичным образом находим миноры для оставшихся элементов матрицы и получаем такой результат.

3. Определяем матрицу алгебраических дополнений. Как их посчитать для каждого элемента мы рассмотрели в отдельной публикации.

Например, для элемента a₁₁ алгебраическое дополнение считается так:

4. Выполняем транспонирование полученной матрицы алгебраических дополнений (т. е. поменяем столбцы и строки местами).

5. Остается только воспользоваться формулой выше, чтобы найти обратную матрицу.

Ответ можем оставить в таком виде, не деля элементы матрицы на число 11, так как в этом случае получится некрасивые дробные числа.

Проверка результата

Чтобы убедиться в том, что мы получили обратную исходной матрицу, мы можем найти их произведение, которое должно равняться единичной матрице.

Недавно мы начали говорить о линейной алгебре и матрицах. Сначала всё было хорошо и легко:

Но начав заниматься линейной алгеброй, бывает трудно остановиться. Сегодня мы познакомимся с обратной матрицей и научимся её вычислять. Это навык, который в будущем нам пригодится для решения матричных уравнений.

С точки зрения арифметики материал не сложный. Но он требует вдумчивого чтения для понимания правил. В итоге статья довольно большая, мозги кипят и танки наши быстры.

Читать ли эту статью?

❌ Если вам нужны простые быстрые решения для жизни — нет, можно объявить, что у вас сегодня выходной.

✅ Если вашему мозгу не хватает вызова и новых горизонтов — велком ту зе матрикс.

Обратное — это как?

В математике есть взаимно обратные числа. Они получаются так: вы берёте какое-то число, добавляете отрицательную степень и получаете обратное число:

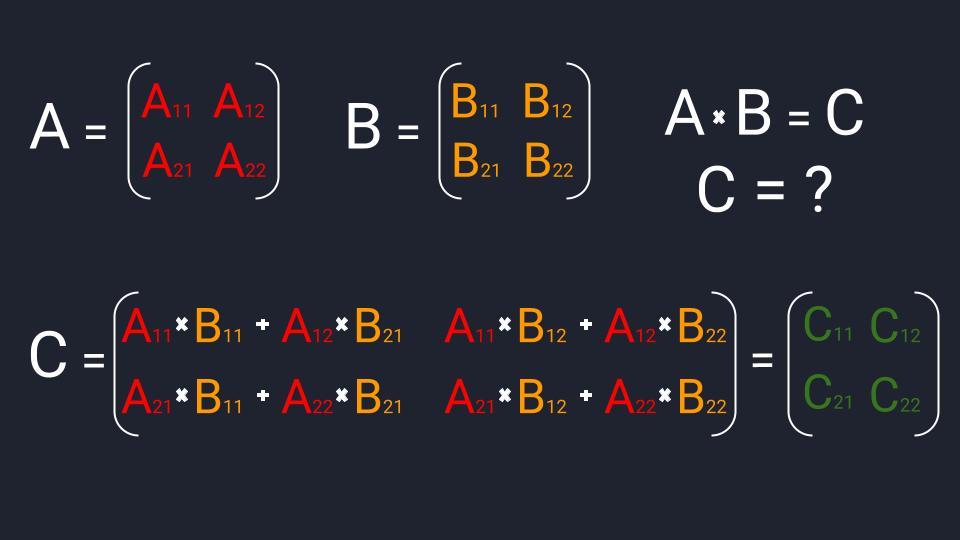
Обратные числа при умножении друг на друга всегда дают единицу:

Обратная матрица

В линейной алгебре есть обратные матрицы. По свойствам они напоминают обратные числа: если обычную матрицу умножить на обратную к ней, получится единичная матрица.

Единичная матрица работает как единица с числами: если умножить любое число на единицу, получится исходное число; если умножить любую матрицу на единичную матрицу — получится исходная матрица:

Единичная матрица состоит из единиц и нулей: на диагонали находятся единицы; остальные элементы — нули. Единичные матрицы не используются при расчёте обратных матриц, но без них не получится решать матричные уравнения.

Пример квадратной единичной матрицы размером 5×5. Единичная матрица может быть любого размера — состоять из любого количества строк и столбцов

Как рассчитать обратную матрицу

Для расчёта обратной матрицы нужно выполнить три действия. Пока что не обращайте внимание на термины:

Разделить единицу на матричный определитель.
Найти транспонированную матрицу алгебраических дополнений.
Перемножить полученные значения.

Далее мы по порядку во всём разберёмся.

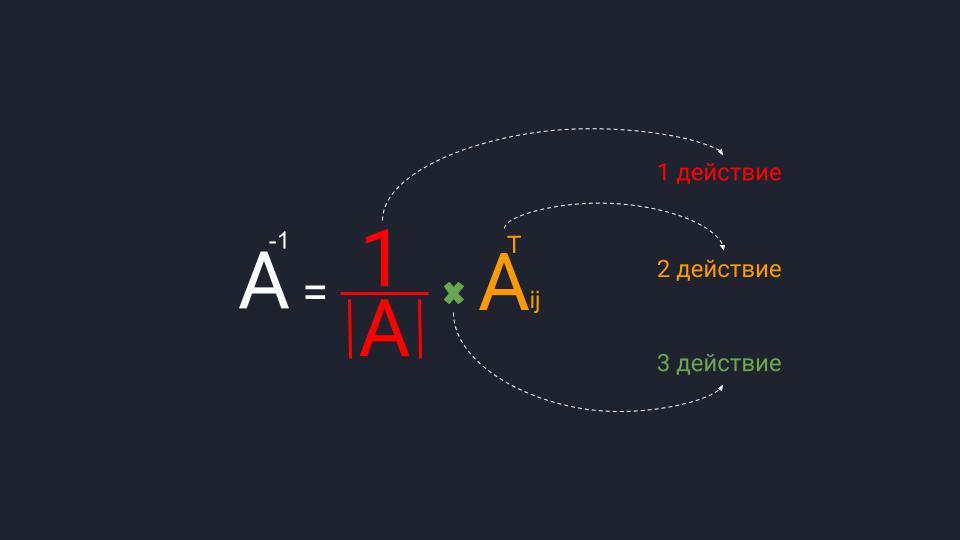
Формула расчёта обратной матрицы: |A| — матричный определитель; Aᵀᵢⱼ — матрица алгебраических дополнений

Порядок вычисления определителя зависит от размера матрицы, которому он соответствует — чем больше матрица, тем сложнее считать определитель. Мы только знакомимся с матрицами, поэтому остановимся на определителях второго и третьего порядка — они подходят для квадратных матриц размером 2×2 и 3×3.

Чтобы найти определитель второго порядка, нам достаточно умножить элементы главной диагонали и вычесть из значения произведение чисел второй диагонали.

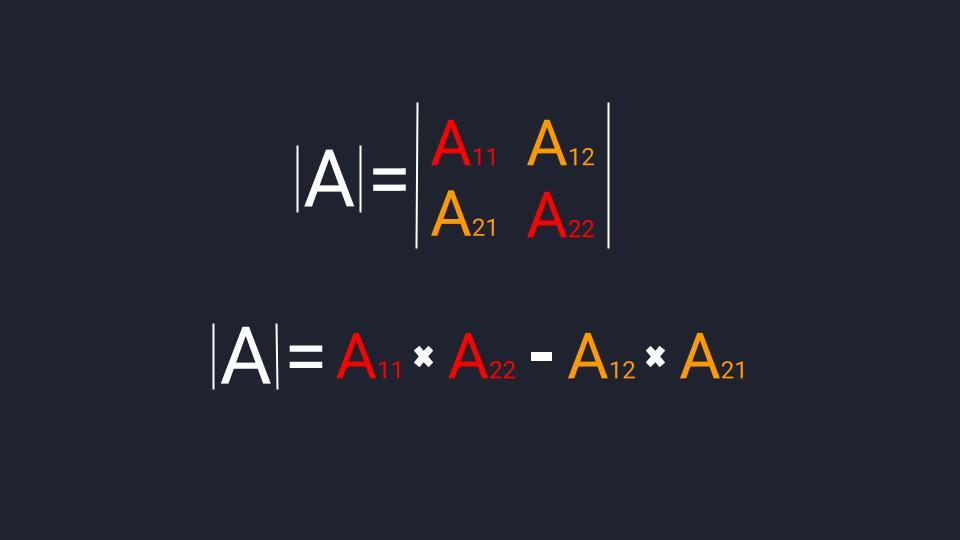
Формула для расчёта определителя второго порядка

Пример расчёта определителя второго порядка

Определитель третьего порядка находится путём умножения диагоналей на треугольники. Здесь много операций, поэтому формулу соберём по частям.

Сначала работаем по главной диагонали: идём от верхнего левого элемента и движемся к правому нижнему элементу. Перемножаем элементы между собой.

Считаем определитель третьего порядка: 1-й этап — главная диагональ

Прибавляем к произведению элементов первой диагонали произведение первого треугольника. Основание первого треугольника находится параллельно главной диагонали и состоит из элементов А₂₁ и А₃₂. Вершина — элементА₁₃.

Считаем определитель третьего порядка: 2-й этап — первый треугольник

Прибавляем к полученному результату произведение второго треугольника, в котором основание состоит из элементов А₁₂ и А₂₃, а вершина — А₃₁.

Считаем определитель третьего порядка: 3-й этап — второй треугольник

Вычитаем из полученного значения произведение элементов второй диагонали. Вторая диагональ начинается в левом нижнем углу и идёт в правый верхний угол.

Считаем определитель третьего порядка: 4-й этап — вторая диагональ

Вычитаем произведение элементов третьего треугольника, в котором основание — элементы А₁₂ и А₂₁, а вершина — А₃₃.

Считаем определитель третьего порядка: 5-й этап — третий треугольник

Последний шаг: вычитаем произведение четвёртого треугольника, с основанием из элементов А₂₃ и А₃₂ и вершиной А₁₁.

Считаем определитель третьего порядка: 6-й этап — четвёртый треугольник

Общий вид формулы для расчёта определителя третьего порядка

Пример расчёта определителя третьего порядка

Транспонированная матрица алгебраических дополнений вычисляется в три шага:

Мы из исходной матрицы находим матрицу миноров.
Меняем в матрице миноров знак некоторых элементов и получаем матрицу алгебраических дополнений.
Находим транспонированную матрицу из матрицы алгебраических дополнений.

Алгоритм вычислений матрицы миноров и матрицы алгебраических дополнений зависит от размера исходной матрицы — чем она больше, тем сложнее формула расчёта. Поэтому мы рассматриваем только матрицы второго и третьего порядка.

Чтобы найти матрицу миноров второго порядка, нам нужно последовательно зачеркнуть три элемента исходной матрицы:

Вычёркиваем первую строку и первый столбец исходной матрицы — получаем первый элемент первой строки матрицы миноров.
Вычёркиваем первую строку и второй столбец — получаем второй элемент первой строки матрицы миноров.
Вычёркиваем вторую строку и первый столбец — получаем первый элемент второй строки матрицы миноров.
Вычёркиваем вторую строку и второй столбец — получаем второй элемент второй строки матрицы миноров.

Когда матрица миноров составлена — меняем знаки элементов второй диагонали и получаем матрицу алгебраических дополнений. Теперь берём эту матрицу и проводим транспонирование — меняем расположение строк и столбцов. Готово.

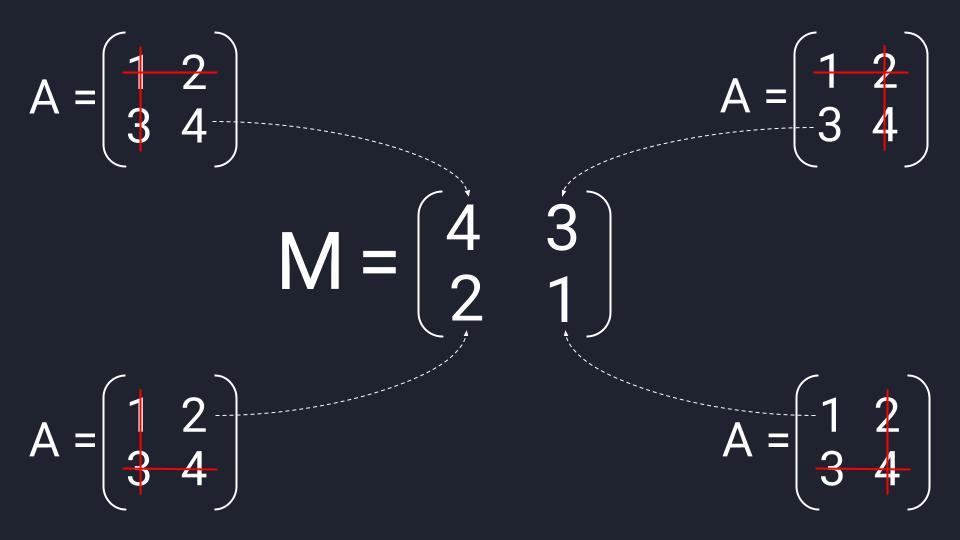
Пример вычисления матрицы миноров из матрицы второго порядка

Пример вычисления матрицы алгебраических дополнений (Aᵢⱼ ) из матрицы миноров второго порядка

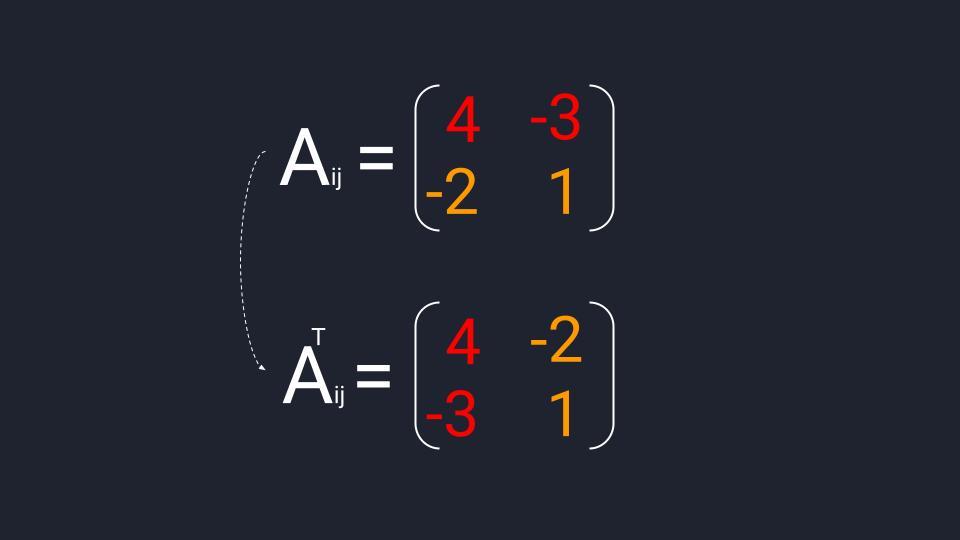
Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров второго порядка

Матрица миноров третьего порядка рассчитывается по следующему принципу:

Последовательно вычёркиваем строки и столбцы.
Получаем четыре элемента и считаем определитель.
Записываем результат в матрицу миноров третьего порядка.

Чтобы не запоминать порядок вычёркивания элементов — попробуйте схему:

Определите элемент, который вы ищете для матрицы. Пусть это будет A₁₁.
Найдите этот же элемент в исходной матрице и отметьте его точкой.
Проведите от этой точки две линии: вдоль строки и вдоль столбца.

После вычёркивания останется квадратная двухразмерная матрица, определитель которой равен разности произведений двух диагоналей.

Пример вычисления первого элемента матрицы миноров из матрицы третьего порядка. Треугольник, или греческая дельта, — это обозначение определителя вне матрицы

Матрицу миноров третьего порядка удобно находить на бумаге с помощью ручки, карандаша и ластика — записываете исходную матрицу, карандашом вычёркиваете линии, считаете определитель, вытираете линии и повторяете процедуру. Рекомендуем попробовать и сверить результат с нашими расчётами.

1-я строка 1-й элемент:

1-я строка 2-й элемент:

1-я строка 3-й элемент:

2-я строка 1-й элемент:

2-я строка 2-й элемент:

2-я строка 3-й элемент:

3-я строка 1-й элемент:

3-я строка 2-й элемент:

3-я строка 3-й элемент:

Считаем матрицу алгебраических дополнений: берём матрицу миноров и меняем на противоположный знак в четырёх элементах — изменяем А₁₂, А₂₁, А₂₃ и А₃₂. Транспонируем полученную матрицу и можем переходить к последнему действию.

Получаем из матрицы третьего порядка матрицу миноров

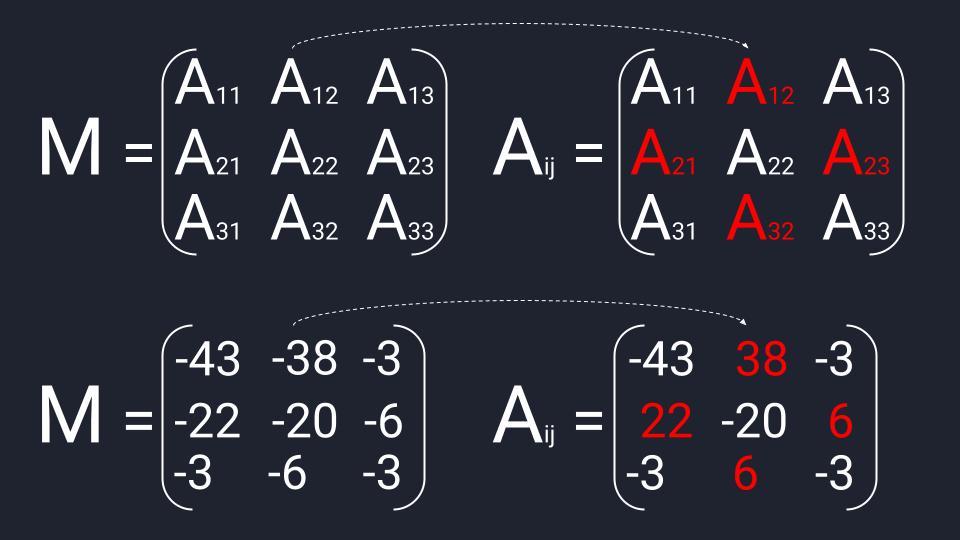
Меняем знаки в матрице миноров и получаем матрицу алгебраических дополнений (Aᵢⱼ)

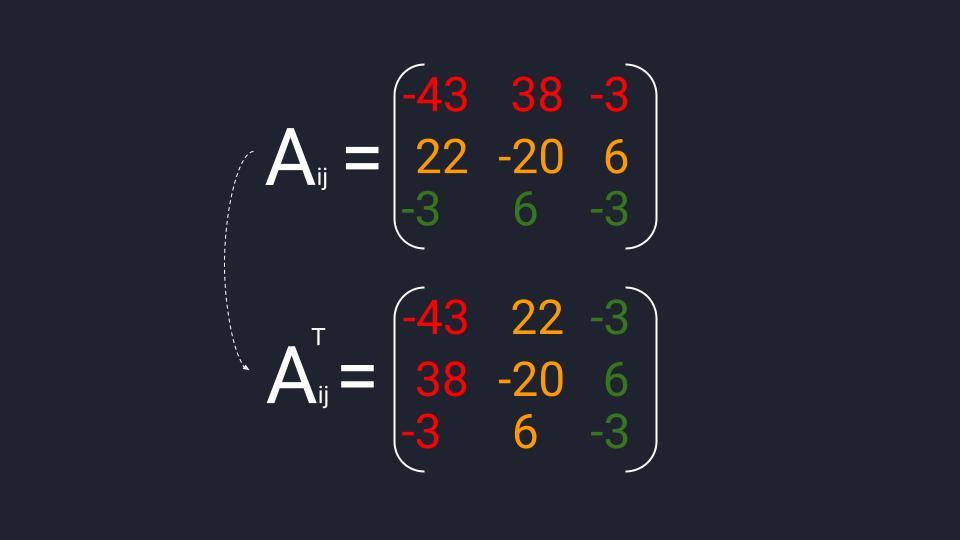
Пример вычисления транспонированной матрицы алгебраических дополнений (Aᵀᵢⱼ), полученной из матрицы миноров третьего порядка

Мы нашли все компоненты для вычисления обратной матрицы. Осталось их подставить в формулу, перемножить и записать ответ:

Пример вычисления обратной матрицы второго порядка: мы внесли дробь в матрицу, но могли этого не делать — просто так захотелось

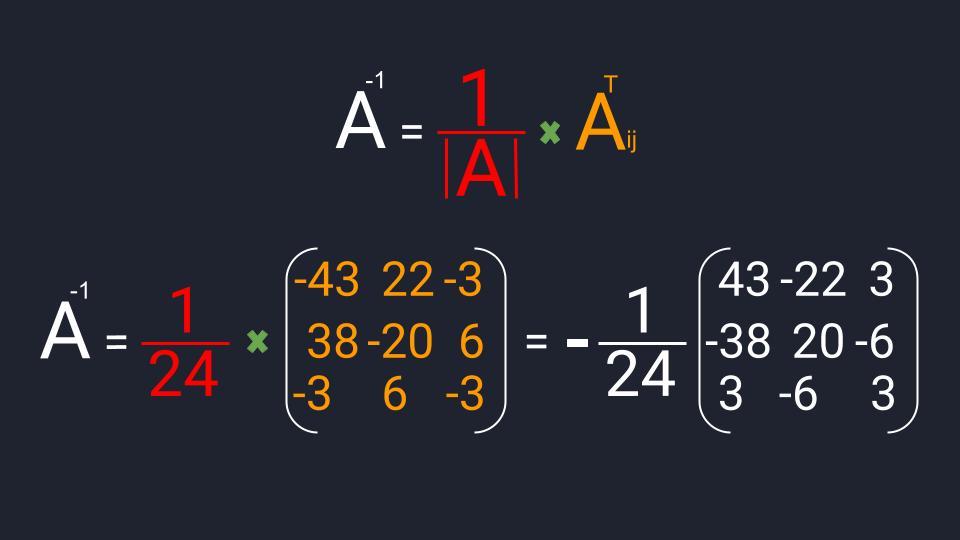
Пример вычисления обратной матрицы третьего порядка: мы оставили дробь за пределами матрицы и вынесли из матрицы минус. Матрица — это таблица с числами, поэтому не обращайте внимание, если числа получаются большими или неудобными

Господи, зачем всё это?

Мы понимаем, что это всё кажется совершенно оторванным от жизни. Какие-то миноры, детерминанты, о чём вообще речь?

для которой справедливо равенство

$A\cdot A^ =A^\cdot A =E$

Для существования обратной матрицы " width="32" height="16" />
необходимо и достаточно, чтобы матрица была невырожденной, то есть, чтобы Пусть задана квадратная матрица a_ & a_ & \ldots & a_ \\ a_ & a_ & \ldots & a_ \\ \ldots & \ldots & \ldots & \ldots \\ a_ & a_ & \ldots & a_ \\ \end \right) ," width="235" height="90" />
тогда обратную к ней матрицу " width="32" height="16" />
можно вычислить по формуле

$A^<-1> =\frac <<\left( \beginA_ & A_ & \ldots & A_ \\ A_ & A_ & \ldots & A_ \\ \ldots & \ldots & \ldots & \ldots \\ A_ & A_ & \ldots & A_ \\ \end \right)>^>=\frac\left( \begin A_ & A_ & \ldots & A_ \\ A_ & A_ & \ldots & A_ \\ \ldots & \ldots & \ldots & \ldots \\ A_ & A_ & \ldots & A_ \\ \end \right)$

где =<<\left( -1 \right)>^>_>" width="143" height="24" />
– алгебраическое дополнение к элементу ." width="26" height="14" />

Примеры вычисления обратной матрицы

$A=\left( \begin 2 & 3 & 7 \\ 1 & -5 & 2 \\ 3 & -1 & 9 \\ \end \right)$

соответствующих элементов матрицы :

$A_<11> =<<\left( -1 \right)>^>\cdot \left| \begin -5 & 2 \\ -1 & 9 \\ \end \right|=-45+2=-43 ; \qquad A_=<<\left( -1 \right)>^>\cdot \left| \begin 1 & 2 \\ 3 & 9 \\ \end \right|=-\left( 9-6 \right)=-3$

$A_<31> =<<\left( -1 \right)>^>\cdot \left| \begin 3 & 7 \\ -5 & 2 \\ \end \right|=6+35=41 ; \qquad A_=<<\left( -1 \right)>^>\cdot \left| \begin 2 & 7 \\ 1 & 2 \\ \end \right|=-\left( 4-7 \right)=3$

$A_<33> =<<\left( -1 \right)>^>\cdot \left| \begin 2 & 3 \\ 1 & -5 \\ \end \right|=-10-3=-13$

составленную из алгебраических дополнений элементов матрицы

$A^<*> =\left( \begin -43 & -3 & 14 \\ -34 & -3 & 11 \\ 41 & 3 & -13 \\ \end \right)$

$A^<-1> Далее запишем обратную матрицу согласно формуле =\frac\cdot <<\left( A^<*>> \right)>^ ,$
получим

$A^<-1> =\frac\cdot \left( \begin -43 & -34 & 41 \\ -3 & -3 & 3 \\ 14 & 11 & -13 \\ \end \right)=\left( \begin \frac\; & \frac\; & \frac\; \\ -1 & -1 & 1 \\ \frac\; & \frac\; & \frac\; \\ \end \right)$

Метод Гаусса для нахождения обратной матрицы

методом Гаусса необходимо:

1) построить вспомогательную матрицу приписав к столбцам матрицы справа столбцы единичной матрицы того же порядка, что и матрица :

$M=\left( \begin a_ & a_ & \ldots & a_ \\ a_ & a_ & \ldots & a_ \\ \ldots & \ldots & \ldots & \ldots \\ a_ & a_ & \ldots & a_ \\ \end\left| \begin 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & 1 \\ \end \right. \right)$

2) элементарными преобразованиями строк привести матрицу к матрице, в левой части которой стоит единичная матрица:

$N=\left( \begin 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & \ldots & 1 \\ \end\left| \begin b_ & b_ & \ldots & b_ \\ b_ & b_ & \ldots & b_ \\ \ldots & \ldots & \ldots & \ldots \\ b_ & b_ & \ldots & b_ \\ \end \right. \right)$

3) матрица, стоящая в правой части полученной матрицы и будет обратной матрицей

$A^<-1> =\left( \begin b_ & b_ & \ldots & b_ \\ b_ & b_ & \ldots & b_ \\ \ldots & \ldots & \ldots & \ldots \\ b_ & b_ & \ldots & b_ \\ \end \right)$

$A=\left( \begin 2 & 3 & 7 \\ 1 & -5 & 2 \\ 3 & -1 & 9 \\ \end \right)$

$M=\left( \begin 2 & 3 & 7 \\ 1 & -5 & 2 \\ 3 & -1 & 9 \\ \end\left| \ \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end \right. \right)$

и приведем её, с помощью элементарных преобразований, к матрице, в которой единичная матрица будет слева. Переставим местами первую и вторую строки

$M=\left( \begin 2 & 3 & 7 \\ 1 & -5 & 2 \\ 3 & -1 & 9 \\ \end\left| \ \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end \right. \right)\tilde\left( \begin 1 & -5 & 2 \\ 2 & 3 & 7 \\ 3 & -1 & 9 \\ \end\left| \ \begin 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end \right. \right)$

Прибавим ко второй строке первую строку, умноженную на а к третьей строке первую, умноженную на

$\left( \begin 1 & -5 & 2 \\ 2 & 3 & 7 \\ 3 & -1 & 9 \\ \end\left| \ \begin 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end \right. \right)\tilde\left( \begin 1 & -5 & 2 \\ 0 & 13 & 3 \\ 0 & 14 & 3 \\ \end\left| \ \begin 0 & 1 & 0 \\ 1 & -2 & 0 \\ 0 & -3 & 1 \\ \end \right. \right)$

Прибавим ко второй строке третью, умноженную на

$\left( \begin 1 & -5 & 2 \\ 0 & 13 & 3 \\ 0 & 14 & 3 \\ \end\left| \ \begin 0 & 1 & 0 \\ 1 & -2 & 0 \\ 0 & -3 & 1 \\ \end \right. \right)\tilde\left( \begin 1 & -5 & 2 \\ 0 & -1 & 0 \\ 0 & 14 & 3 \\ \end\left| \ \begin 0 & 1 & 0 \\ 1 & 1 & -1 \\ 0 & -3 & 1 \\ \end \right. \right)$

Умножим вторую строку на

$\left( \begin 1 & -5 & 2 \\ 0 & -1 & 0 \\ 0 & 14 & 3 \\ \end\left| \ \begin 0 & 1 & 0 \\ 1 & 1 & -1 \\ 0 & -3 & 1 \\ \end \right. \right)\tilde\left( \begin 1 & -5 & 2 \\ 0 & 1 & 0 \\ 0 & 14 & 3 \\ \end\left| \ \begin 0 & 1 & 0 \\ -1 & -1 & 1 \\ 0 & -3 & 1 \\ \end \right. \right)$

Прибавим к первой строке вторую, умноженную на а к третьей вторую, умноженную на

$\left( \begin 1 & -5 & 2 \\ 0 & 1 & 0 \\ 0 & 14 & 3 \\ \end\left| \ \begin 0 & 1 & 0 \\ -1 & -1 & 1 \\ 0 & -3 & 1 \\ \end \right. \right)\tilde\left( \begin 1 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \\ \end\left| \ \begin -5 & -4 & 5 \\ -1 & -1 & 1 \\ 14 & 11 & -13 \\ \end \right)$

Разделим третью строку на 3

$\left( \begin 1 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \\ \end\left| \ \begin -5 & -4 & 5 \\ -1 & -1 & 1 \\ 14 & 11 & -13 \\ \end \right. \right)\tilde\left( \begin 1 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end\left| \ \begin -5 & -4 & 5 \\ -1 & -1 & 1 \\ \frac\; & \frac\; & \frac\; \\ \end \right)$

К первой строке прибавим третью, умноженную на

$\left( \begin 1 & 0 & 2 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end\left| \ \begin -5 & -4 & 5 \\ -1 & -1 & 1 \\ \frac\; & \frac\; & \frac\; \\ \end \right. \right)\tilde\left( \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end\ \ \left| \ \begin \frac\; & -\frac\; & \frac\; \\ -1 & -1 & 1 \\ \frac\; & \frac\; & \frac\; \\ \end \right. \right)$

Читайте также: