Как сделать нормировку в эксель
Обычно выраженность некоторого качества пытаются описать числом. Чаще всего такое число х формируется как сумма баллов. Насколько это правомерно — вопрос другой. Мы же предположим, что такое число х получено и осмысленно.
Обычно х меняется от некоторого минимального значения xmin (отражающего отсутствие качества) до некоторого максимального значения xmax (крайняя степень проявления, наличия, выраженности, …).
Его получение решает проблему сравнения двух объектов, но только по этому показателю. Впрочем, и здесь дело не очень хорошо. Надо всегда помнить, в каких пределах меняется показатель. А эти диапазоны — самые разнообразные… Да еще и оценивать, насколько близко конкретное значение к краям диапазона или к его середине. В общем, чистая морока.
Если же речь идет о сравнении по двум различным показателям — дело совсем швах. Конечно, нельзя сравнивать качества непосредственно. Для этого сравниваемые числа должны быть безразмерными. А ведь именно показатель обычно интерпретируется как степень выраженности некоторого качества. И вот это сравнивать можно. Но для этого их следует привести к одной шкале так, чтобы начала и концы двух шкал совпадали.
Но почему только этих двух? Давайте сделаем такое преобразование для всех показателей! Оно и называется нормировкой (не путать с нормализацией!). После этого мы можем сравнивать разнообразные показатели, полученные различными методиками.
2. Типы показателей
При всем разнообразии числовых характеристик объектов (или респондентов) из них можно выделить два широких класса:
3. Нормировка униполярного показателя
Давно сложилось в науке так, что величины нормируются на диапазон от 0 до 1.
Для этого функция преобразования y=f(x) должна обладать следующими свойствами:
Любая функция с такими свойствами м.б. использована для нормировки. Например, если xmax , то можно выбрать функцию
Легко видеть, что за счёт выбора соответствующей функции можно учесть разнообразные эффекты искажения оценок. Например, склонность респондента к крайним оценкам. При этом, возможно, следует применять для различных респондентов и различные функции преобразования, учитывающие особенности их личности, статуса и т.п. Примерные графики таких функций — на рис. 1.
Рис. 1. Графики функции нормировки
Наиболее часто применяется линейное преобразование:
Если полагать, что увеличение х описывает как возрастание выраженности качества А, так и убывание степени некоторого другого качества В, то нормированной мерой качества В может служить просто разность y´=1–y. Таковы, например, родственные по смыслу качества ‘близость’ и ‘дистанция’. Их метризация выявляет плохо осознаваемую ранее, но вполне четкую дополнительность и даже противоположность.
4. Нормировка биполярного показателя
Обычно такой показатель представляет собой ‘склейку’ двух взаимопредполагающих и антонимичных униполярных качеств А и В.
Пусть величина х оценивает степень выраженности обоих качеств (с соответствующим обозначением, например, ‘очень люблю’ или ‘слегка ненавижу’). Нормировку можно проводить при помощи любой функции, удовлетворяющей условиям (1). В частности, это м.б. и линейное преобразование:
Очевидно, что y[–1; +1].
Обе формулы (2) и (3) описывают линейное преобразование вида y=k·x+b. Поэтому все статистические выводы относительно величин x и y полностью совпадают.
5. Особенности балльных шкал
При использовании балльной шкалы имеется несколько тонкостей, которые часто упускаются из виду:
При нормировке балльной шкалы надо всего лишь принять, что х = S, где S сумма набранных баллов по полученным ответам (а не заданных вопросов!). Соответственно, Smin и Smax — минимальная и максимальная суммы баллов, которые можно набрать при полученных ответах.
Здесь bmin и bmax — наименьшее и наибольшее значения баллов. При этом у меняется в диапазоне от 0 до 1. Границы ‘0’ он достигает при всех ответах, равных bmin, а ‘1’ — равных bmax.
Для нормировки балльного показателя на дипазон [-1; 1] надо пользоваться формулой:
Нормально делай – нормально будет: нормализация на практике – методы и средства Data Preparation
Нормально делай – нормально будет: нормализация на практике - методы и средства Data Preparation
Мы уже рассказали, что такое нормализация данных и зачем она нужна при подготовке выборки (Data Preparation) к машинному обучению (Machine Learning) и интеллектуальному анализу данных (Data Mining). Сегодня поговорим о том, как выполняется нормализация данных: читайте в нашем материале о методах и средствах преобразования признаков (Feature Transmormation) на этапе их генерации (Feature Engineering).
Нормализация данных: методы и формулы
Существует множество способов нормализации значений признаков, чтобы масштабировать их к единому диапазону и использовать в различных моделях машинного обучения. В зависимости от используемой функции, их можно разделить на 2 большие группы: линейные и нелинейные. При нелинейной нормализации в расчетных соотношениях используются функции логистической сигмоиды или гиперболического тангенса. В линейной нормализации изменение переменных осуществляется пропорционально, по линейному закону.

На практике наиболее распространены следующие методы нормализации признаков [1]:
- Минимакс – линейное преобразование данных в диапазоне [0..1], где минимальное и максимальное масштабируемые значения соответствуют 0 и 1 соответственно;
- Z-масштабирование данных на основе среднего значения и стандартного отклонения: деление разницы между переменной и средним значением на стандартное отклонение;
- десятичное масштабирование путем удаления десятичного разделителя значения переменной.
На практике минимакс и Z-масштабирование имеют похожие области применимости и часто взаимозаменяемы. Однако, при вычислении расстояний между точками или векторами в большинстве случае используется Z-масштабирование. А минимакс полезен для визуализации, например, чтобы перенести признаки, кодирующие цвет пикселя, в диапазон [0..255] [2].
Как нормализовать данные для машинного обучения и Data Mining
Чтобы выполнить нормализацию данных, нужно точно знать пределы изменения значений признаков: минимальное и максимальное теоретически возможные значения. Этим показателям будут соответствовать границы интервала нормализации. Когда точно установить пределы изменения переменных невозможно, они задаются с учетом минимальных и максимальных значений в имеющейся выборке данных [3].
На практике data scientist нормализует данные с помощью уже готовых функций интегрированных сред для статистического анализа, например, IBM SPSS, SAS или специальных библиотек: Scikit-learn, Auto-sklearn, pandas и т.д. Кроме того, аналитик данных может написать собственный код на языке R или Python для почти любой операции Data Preparation [4].

Синтаксис
Формула нормального распределения в Excel включает 4 аргумента.
- ИКС: Это обязательный аргумент для функции НОРМРАСП в excel. Это значение, необходимое нам для расчета нормального распределения в Excel.
- Значить: Это среднее значение распределения, т.е. Среднее значение.
- Среднеквадратичное отклонение: Это стандартное отклонение распределения точек данных.
- Накопительный: Это логическое значение. Упоминая TRUE или FALSE, мы должны указать тип распределения, которое мы собираемся использовать. TRUE означает кумулятивную функцию нормального распределения, а FLASE означает функцию нормальной вероятности.
- Заметка: В Excel 2010 и более ранних версиях вы можете увидеть нормальное распределение в Excel, но в 2010 и более поздних версиях оно заменено функцией НОРМРАСП в Excel. Хотя нормальное распространение в Excel все еще существует в последних версиях, оно может быть недоступно позже. Он по-прежнему существует для поддержки совместимости.
Как использовать НОРМРАСП в Excel? (с примерами)
У меня есть данные о курсах акций одной из компаний. Их установленная цена акций составляет 115, общая средняя цена акций — 90, а значение SD — 16.
Нам нужно показать вероятность того, что цена акции находится на уровне 115.
Позвольте мне применить кумулятивный НОРМРАСП в Excel.
X мы выбрали начальную цену акции, а в качестве среднего мы взяли общую среднюю цену, а для SD мы рассмотрели значение ячейки B4 и использовали TRUE (1) в качестве типа распределения.
Результат равен 0,9409, что означает 94% графика цены акции в этом диапазоне.
Если я изменю тип распределения на нормальное распределение (FALSE — 0), мы получим следующий результат.
Это означает 0,74% от цены акции в этом диапазоне.
Позвольте мне рассмотреть приведенные ниже данные для нормального распределения в Excel.
- Выборка совокупности, т. Е. X равно 200
- Среднее или Среднее значение 198
- Стандартное отклонение 25
Применение кумулятивного нормального распределения в Excel
Значение нормального распределения Excel составляет 0,53188, т. Е. 53,18% — это вероятность.
Некоторые методы обработки многомерных статистических данных требуют предварительной нормировки данных. Нормировка данных состоит в преобразовании данных к новой форме представления. Такие преобразования позволяют исключить влияние на результаты анализа принятых единиц измерения. Рассмотрим наиболее распространенные способы нормировки:
- нормировка по максимальному значению;
- нормировка по минимальному значению;
- нормировка по среднему значению.
Приведем формулы для выполнения нормировок (5.1)-(5.4):
Рассмотрим пример выполнения нормировки признаков X и Y. Исходные значения признаков приведены на рис. 5.1.
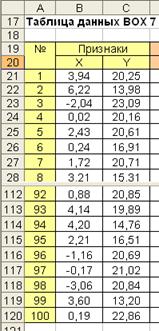
Рис. 5.1. Исходные значения признаков X и Y
Результаты расчета параметров признаков X и Y приведены на рис. 5.2. Коэффициент корреляции равен -0, 62. Результаты выполнения операции нормировки приведены на рис. 5.3.
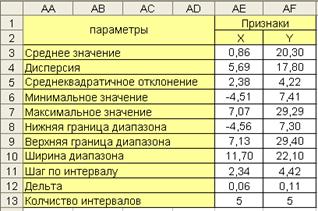
Рис. 5.2. Расчет параметров признаков X и Y
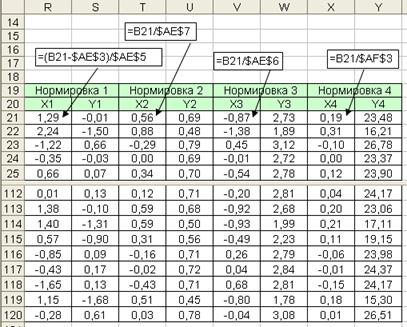
Рис. 5.3. Результаты нормировки признаков X и Y
Нормировка центрирование может быть выполнена с помощью функции EXCEL НОРМАЛИЗАЦИЯ (рис. 5.4).
Читайте также:


