Как сделать наклонный цилиндр

Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. ( Вспомните : наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть. )
Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180 ° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники .
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).
Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).
б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB 1 A 1 и его ось OO 1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O 1 и осями — отрезки АВ и A 1 В 1 . Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.



в) Касательная плоскость к цилиндру.
Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).

Говорят, что плоскость α касается цилиндра ( цилиндрической поверхности ) по образующей DD 1 , каждая точка образующей DD 1 является точкой касания плоскости α и данного цилиндра.
Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.
17.3. Развёртка и площадь поверхности цилиндра

Развёртку цилиндра мы также введём на интуитивном уровне.
Пусть R — радиус основания, h — высота цилиндра.


Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.
За площадь боковой поверхности цилиндра принимается площадь её развёртки , т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:
Таким образом, доказана следующая теорема.

Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼
Площадь круга радиуса R равна π R 2 , поэтому S осн = π R 2 . Тогда для нахождения площади полной поверхность цилиндра справедливо:
S полн = S бок + 2 S осн = 2 π Rh + 2 π R 2 = 2 π R ( R + h ) .

Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156) . Тогда
S бок = 2 π DC • BC . (1)

Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: S бок = 2 π EF • AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.
Это следствие найдёт своё применение в п. 19.7.
17 . 4 . Призмы, вписанные в цилиндр и описанные около цилиндра
Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.
Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.
Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).

Цилиндр в этом случае называют описанным около призмы.
Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.
Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.

Цилиндр при этом называют вписанным в призму (рис. 158).
Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим , соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.
При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.
Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.

На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а ); правильная четырёхугольная призма (рис. 159, б ); правильная треугольная призма (рис. 159, в ); правильная шестиугольная призма (рис. 159, г ).

ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a . Найти площади боковой и полной поверхностей правильной призмы, вписанной в этот цилиндр, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.

Решени е. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA 1 B 1 C 1 (рис. 160); CDD 1 C 1 — осевое сечение; OO 1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.

Так как цилиндр — равносторонний, то CDD 1 C 1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD 1 С 1 находим CD = = a = h.
Далее, △ АВС — правильный, вписанный в основание, радиус которого R = = . Значит, сторона АВ и высота СЕ этого треугольника равны: АВ = R = , СЕ = R = a. Откуда
S осн = = ;
S бок = 3 S ABB 1 A 1 = 3 AB • BB 1 = 3 • • a = .
S полн = S бок + 2 S осн = + 2 • = .
Ответ: a) ; .

ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решени е. Рассмотрим случай б). Пусть ABCDA 1 B 1 C 1 D 1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO 1 цилиндра и скрещивающейся с ней (почему?) диагональю АB 1 боковой грани ABB 1 A 1 данной призмы.
Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.
Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB 1 и OO 1 равно расстоянию между плоскостью грани ABB 1 A 1 и параллельной ей (почему?) плоскостью сечения EFF 1 E 1 . Это расстояние равно длине отрезка ОK (где точка K — середина АВ ), так как OK ⟂ ( ABB 1 ) и ( ABB 1 ) || ( EFF 1 ) .
Поскольку данный цилиндр — равносторонний, то BDD 1 B 1 — квадрат со стороной BD = ВВ 1 = a. Тогда АВ = = . Значит, ОK = АЕ = = — искомое расстояние между прямыми ОО 1 и АВ 1 .
Обозначим ∠ ( OO 1 ; AB 1 ) = ϕ , M = AB 1 ∩ A 1 B. Для нахождения угла ϕ проведём в грани ABB 1 A 1 прямую KK 1 || OO 1 . Тогда ϕ = ∠ ( OO 1 ; AB 1 ) = ∠ ( KK 1 ; AB 1 ) . Так как KK 1 || OO 1 , OO 1 ⟂ ( ABC ) , то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = , KМ = . Значит, tg ϕ = = , откуда ϕ = arctg .
Ответ: б) , arctg .

Во многих пособиях по геометрии за площадь боковой поверхности цилиндра принимают предел последовательности площадей боковых поверхностей правильных вписанных в цилиндр (или описанных около цилиндра) n- угольных призм при n → + ∞ .

Действительно, S бок. пов. призм = h • P осн. призм , где Р осн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: S бок = 2 π Rh.
17.5. Объём цилиндра
Напомним принятое нами соглашение, основанное на принципе Кавальери.

Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π • R 2 : R 2 = π : 1. Тогда и для объёмов этих тел справедливо: V цил : V парал = π : 1 или V цил : ( R 2 • h ) = π : 1, откуда
V цил = π • R 2 • h.
Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле



Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = π • R 2 • h.
Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:

V= π • R 2 • ( a + b ),

где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.

Дано: Пересечение конуса и цилиндра - две пересекающиеся поверхности - поверхность прямого конуса и цилиндра - линия их пересечения.
Необходимо: Сделать развертку цилиндра и нанести на ней линию их пересечения.
В предыдущем видеоуроке "Развертка конуса" мы построили приближенную развертку конуса, вписав в конус правильную 12 гранную пирамиду. Построение развертки цилиндра также сделаем приближенно, разделив основание цилиндра на 12 частей.
Как сделать развертку цилиндра (алгоритм)
Решение задач по начертательной геометрии я произвожу в системе автоматизированного проектирования Автокад и Автокад 3D. Данный прием обучения позволит развить пространственное мышление и закрепить владение Автокад.
- Строим развертку боковой поверхности цилиндра.
- Делим основание цилиндра на 12 равных частей.
- Измеряем хорду между двумя любыми соседними точками деления окружности основания и откладываем это расстояние по нижней стороне развертки цилиндра.
Построение развертки боковой поверхности цилиндра
Развертка боковой поверхности прямого цилиндра представляет из себя прямоугольник. Высота прямоугольника равна высоте цилиндра, а его длина равна длине окружности основания.
![Боковая развертка поверхности прямого цилиндра.]()
![Развертка боковой поверхности цилиндра пересекающегося с конусом.]()
Так как нам требуется построить развертку боковой поверхности цилиндра пересекающегося с конусом, то данная развертка будет представлять из себя прямоугольник с вырезами.
Будем использовать упрощенный способ пострения развертки боковой поверхности цилиндра. Для этого разделим его основание на 12 равных частей на фронтальной плоскости проекции. Это можно сделать, вписав правильный многоугольник в окружность.
Отметим характерные точки пересечения вершин двенадцатиугольника с окружностью. На рисунке эти точки обозначены засечками-крестиками. Соединяем эти точки отрезками - хордами.
Начертите развертку боковой поверхности цилиндра, взяв высоту прямоугольника из горизонтальной плоскости проекции цилиндра. Длину прямоугольника возмите из фронтальной плоскости проекции цилиндра, которая будет равна длине 12 хорд. Измерьте длину любой хорды и отложите ее 12 раз на развертке поверхности цилиндра.
Как сделать развертку основания прямого цилиндра
Основанием прямого цилиндра является круг. Цилиндр имеет два основания: верхнее и нижнее. Следовательно возьмите радиус основания цилиндра на фронтальной или горизонтальной его плоскости проекции и присоедините его к боковой развертке цилиндра, как показано на рисунке.
Построение линии пересечения прямого цилиндра с конусом на развертке поверхности цилиндра
Так как образующие цилиндра проецируются в натуральную величину на горизонтальной плоскости проекции (цилиндр фронтально проецирующий), то мы будем брать на ней координаты точек от его основания до линии пересечения и переносить на развертку цилиндра по порядку. Нумерацию образующих цилиндра смотрите на рисунке (вы можете выбрать для себя любую последовательность снятия координат их линии пересечения для развертки цилиндра, главное не запутаться).
Я покажу принцип снятия координат нескольких точек линии их взаимного пересечения и нанесения их на боковую развертку цилиндра, остальные сделаете по подобию.
Вы уже имеете 12 образующих цилиндра, которые получили при построении его боковой развертки и по сути можете на них опираться, чтобы не запутаться в образующих цилиндра. Также уже есть характерные точки линии их пересечения на фронтальной и горизонтальной плоскости проекции, требуется только их перенести на боковую развертку поверхности цилиндра!
Определите первую крайнюю опорную точку пересеченя цилиндра с конусом. Она находится на определенном расстоянии от 3 образующей цилиндра, которое можете измерить на фронтальной плоскости проекции и отложить от 3 образующей на развертке цилиндра. Далее на его развертке чертите дополнительную образующую и откладывайте данную точку. Эта точка лежит на оси симметрии боковой поверхности цилиндра, середине образующей.
Вы можете построить дополнительную линию на развертке боковой поверхности цилиндра, которая будет делить ее пополам. Это необходимо для удобства проставления координат симметриченых точек линии пересечения цилиндра с конусом на развертке, чтобы не откладывать каждую точку от основания цилиндра, а от "оси симметрии".
Нанесите следующие точки линии их пересечения на боковую разветку цилиндра. Они лежат на определенном расстоянии от 4 образующей цилиндра и проецируются на фронтальную плоскость проекции в одну точку, так как цилиндр форонтально проекцирующий. Измерьте это расстоняение и отложите его на развертке цилиндра от 4 образующей. Проведите вспомогательную образующую на развертке. Теперь на этой образующей цилиндра необходимо проставить точки линии их пересечения координаты которых, вы можете взять на горизонтальной плоскости проекции.
Таким образом вы переносите все точки линии пересечения цилиндра и конуса на развертку поверхности цилиндра и соединяете их плавной линией.
29 декабря, 2013 Анна Веселова
![Cilindr usechennihyj]()
![kursy kompas 3d v20]()
Здравствуйте друзья! На этом уроке мы будем строить сечение цилиндра плоскостью и развертку усеченного цилиндра.
За основу возьмем модель цилиндра, построенного на втором уроке по 3d моделированию.
Последовательность построения усеченного цилиндра
Пункты 1 — 4 аналогичны пунктам построения чертежа усеченной призмы .
5. От оси симметрии цилиндра откладываем расстояние до следа секущей плоскости – 32 мм, проводим след секущей плоскости Pv под углом 60º.
6. Обозначаем несколько точек пересечения поверхности цилиндра со следом плоскости. Находим их на проекциях цилиндра. Соединяем точки при помощи кривой Безье. Получаем искаженные фигуры сечений.
![]()
Для того, чтобы найти точки 2 и 3 разделите окружность на горизонтальной проекции цилиндра на 12 равных частей. И только потом по линиям связи находите их проекции на фронтальной!
![peresechenie ploskostjyu cilindra]()
7. Построим натуральный вид сечения
Построение натурального вида сечения цилиндра
8, 9 Построение аналогично построению сечения призмы
![naturaljnihyj vid secheniya cilindra]()
Развертка усеченного цилиндра
10. Развертку цилиндра будем строить на одной линии с осями x и y1.
![razvertka usechennogo cilindra]()
11. Откладываем отрезок длиной l=π*D=3,14*40=125,6 мм.
12. Делим этот отрезок на 12 равных частей, нумеруем.
13. Переносим высоты отрезков с фронтальной проекции цилиндра. Соединяем полученные вершины при помощи кривой Безье. Натуральный вид сечения переносим копированием и поворотом. Достраиваем нижнее основание цилиндра.
Построение изометрии цилиндра
14. Наглядное изображение цилиндра сделаем при помощи рисунка. Для этого необходимо пересечение плоскостью цилиндра (3d модели).
15. Открываем деталь, в дереве модели выбираем плоскость xy. Строим эскиз, показанный на рисунке.
![peresechenie cilindra sekutheyj ploskostjyu]()
![izometriya cilindra]()
17. Сохраняем деталь в формате рисунка и вставляем его в чертеж. Оформляем чертеж.
![Cilindr usechennihyj]()
Для лучшего понимания материала советую посмотреть небольшое видео по теме.
![]()
Как видите, построение сечения цилиндра плоскостью и развертки усеченного цилиндра, не такая уж и сложная задача вообще, а в Компасе построение идет гораздо проще.
![]()
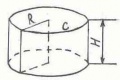
Цилиндр - это, к примеру, консервная банка из-под зелёного горошка. Если мы открывашкой по кругу вскроем до конца оба донышка, а потом то, что осталось, - боковину - разрежем по вертикали и распрямим на плоскости, то как раз и получится развёртка цилиндра - развёрнутые в прямоугольник боковые стенки и два донышка-кругляшка.
![]()
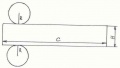
Если же развёртку нужно делать из бумаги, поступаем следующим образом. Строим с помощью циркуля два круга одинакового радиуса R. Это будут основания цилиндра. Затем строим боковую поверхность цилиндра. Она, как мы уже знаем из опыта с банкой, представляет собой прямоугольник. Длина этого прямоугольника будет такой же, как длина окружности оснований L. А длина окружности, согласно формуле, будет равна: L = 2πR, где R - радиус оснований, а π=3,14. Высота прямоугольника будет равна высоте нашего цилиндра - обозначим её как h.
Если требуется реальная выкройка для склеивания цилиндра, то вдоль сторон L боковой поверхности делаем припуск на склейку в виде полос, которые вырезаем зубцами, для приклеивания донышек. А вдоль одной стороны h делаем припуск в виде сплошной полосы для склеивания боковой поверхности цилиндра.
Ну, а если мы уже разучились чертить с помощью циркуля и прочих старинных инструментов, можно всё вышеперечисленное выполнить на компьютере, скажем, в программе Autocad.
Поверхность цилиндра состоит из двух равных кругов радиуса R и прямоугольника, ширина которого равна высоте цилиндра, длина вычисляется по формуле С=2пR , где п=3,14. Изображение цилиндра и его развертка на рисунках:
![]()
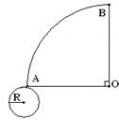
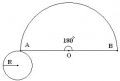
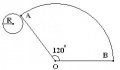
Поверхность конуса состоит круга радиуса R и сегмента круга радиуса OA. Дуга АВ=2пR. Изображение конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга АВ=2пR, надо чтобы АО=4R
б) Когда угол развернутый имеем половину круга. Чтобы дуга АВ=2пR, надо чтобы АО=2R
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AB=2пR, надо чтобы АО=3R
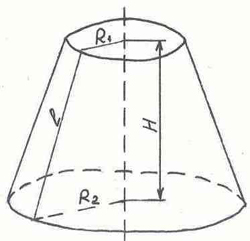
Поверхность усеченного конуса состоит двух кругов радиуса R1 , R2 и сегмента круга радиуса OA. Дуга AB=2пR. Изображение усеченного конуса и его разверток показаны на рисунках:
а) Когда угол прямой имеем четверть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=4R1, В1О=4R2
б) Когда угол развернутый имеем половину круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=2R1, В1О=2R2
в) Когда угол 120 градусов имеем треть круга. Чтобы дуга AA1=2пR1, и дуга BB1=2пR надо чтобы А1О=3R1, В1О=3R2
Читайте также: