Как сделать мультиплексор logisim
В настоящее время я учусь в старших классах средней школы, и меня интересует компьютерная / электротехника, в частности, разработка микропроцессоров. Я прочитал Code Чарльза Петцольда и начал читать Wikibook Design Microprocessor Design (который кажется неполным). Благодаря чтению Code я понимаю основную логику ЦП и начал строить ее в LogiSim. Глава 17 в Кодексе подробно описывает процессор, который я хочу построить, но в схемах отсутствуют ключевые компоненты - тактовые сигналы и декодирование команд. Некоторые из тактовых сигналов кажутся довольно очевидными (кажется, что ПК нужен устойчивый тактовый сигнал), но другие (например, как зафиксировать значения оперативной памяти) мне пришлось продумать и попытаться начать работать.
Я могу построить работающий аккумулятор (он не может быть точно назван ALU, я думаю, потому что в нем отсутствует L-часть), который переключается между сложением и вычитанием с помощью одного входа, и я понимаю, что это все, что мне нужно для арифметической части - как только я получу коды операций перехода, я могу реализовать умножение и деление в коде. Часть, с которой я борюсь - это декодирование команд. Посредством некоторых поисков в Google я вижу, что каждый код операции должен интерпретироваться как множественные микроинструкции, но я теряюсь в том, как мне нужно, чтобы это работало. В настоящее время мой декодер команд представляет собой просто схему комбинационного анализа с одним двоичным выходом для каждого кода операции - всего 13.
Я чувствую, что мне не хватает большой информации о декодировании команд и о том, как мне нужно делать тактовые сигналы .
PetzoldMk5 является основным процессором, который полагается на другие файлы, которые будут импортированы как библиотеки.
Вот список кодов операций (все двоичные):
Зато сам сделал.
Так как блог личный, то и пишу почти для себя. Давней мечтой, идеей фикс (с того самого времени как меня заинтересовала электроника), было желание спроектировать свой процессор, CPU. Вот что пока получилось, можно наблюдать ниже. Оказывается это очень просто! Сделано в программе Logisim, которая хоть и не без недостатков, но позволяет легко симулировать цифровую электронику.

Данный процессор разрабатывался в рамках создания узкоспециализированного сопроцессора одного, в дальнейшем после доработок будет перенесен в квартус под мелкую кплд. Архитектура – что-то типа CISC. Он не обязательно должен быть сверхпроизводительным, но обязательно уметь быстро считать, точнее включать отдельный блок, который производит все аппаратные вычисления за 2.5 такта беря данные с двух регистров и помещая их в аккумулятор (первый — A, второй — B). Здесь, для наглядности вместо него обыкновенный сумматор. Понимаю, что можно было более оптимально все сделать, на меньшем количестве логических элементов, например, объединить вместе ИЛИ подтверждения инкрементирования адреса и т.д., но пока и так сойдет. Процессор способен выполнять ~8 команд, нераспознанные опкоды трактуются как NOPE. Команды хранятся в ПЗУ.
Команды и их коды:
LDA – 0a – загрузить в регистр A константу.
LDB – 0b – скопировать в регистр B данные из регистра A.
IN – 31 – загрузить в регистр A данные из ОЗУ.
OUT – 32 – загрузить данные из регистра A в ОЗУ.
FUNC – 21 – обработать регистры A и B и поместить результат в A.
BREQ – 70 – перейти по адресу если регистр А равен нулю.
GOTO – 77 – безусловный переход.
HALT – 80 – останов.
Федеральное государственное бюджетное образовательное учреждение
высшего образования
"МИРЭА - Российский технологический университет"
РТУ МИРЭА
Выполнил студент группы ИВБО-01-18
Схемы, реализующие логическую функцию на мультиплексорах требуемыми способами ………………………………………………..4
Реализация логической функции на мультиплексоре 16-1. …….4
Реализация логической функции на мультиплексорах 4-1…………….………………………………………………………. 7
Реализация логической функции на комбинации мультиплексоров 4-1 и 2-1…………………………………………..
Постановка задачи и персональный вариант.
Схемы, реализующие логическую функцию на мультиплексорах требуемыми способами
Реализация логической функции на мультиплексоре 4-16
Реализация логической функции на мультиплексорах 4-1
Реализация логической функции на комбинации мультиплексоров 4-1 и 2-1
–используя один мультиплексор 16-1;
–используя минимальное количество мультиплексоров 4-1;
–используя минимальную комбинацию мультиплексоров 4-1 и 2-1.
Протестировать работу схем и убедиться в их правильности. Подготовить отчет о проделанной работе и защитить ее.
Преобразуем ее в двоичную запись: – получаем столбец значение логической функции, который необходим для восстановления полной таблицы истинности (см. табл.1)
Таблица 1
a | b | c | d | F |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 1 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 1 |
Для реализации заданной функции на мультиплексоре 16-1 выполним следующее.
Разместим мультиплексор на рабочей области лабораторного комплекса и сделаем ему следующие настройки:
На адресные (выбирающие) входы мультиплексора подадим при помощи шины значения логических переменных. Несмотря на использование шины, следует помнить, что младшая переменная подается на младший адресный вход, а старшая –на старший.

Собранная и протестированная схема показана на рис. 1. Тестирование подтвердило правильность работы схемы.
Рис. 1 Тестирование схемы, реализующей логическую функцию на мультиплексоре 16-1
Тестирование показало, что схема работает правильно.
Однако мы можем в качестве адресных переменных выбрать любые три из имеющихся, а оставшуюся четвертую рассматривать наравне с логическими константами как элемент исходных данных для информационных входов.
Удобнее всего в качестве адресных переменных взять три старшие переменные нашей функции, т.е. a, b, c. Тогда пары наборов, на которых эти переменные будут иметь одинаковое значение, будут располагаться в соседних строчках таблицы истинности и поэтому можно будет легко увидеть, как значение логической функции для каждой пары наборов соотносится со значением переменной d(рис. 2).
Например, из рис. видно, что для первой строчки . Всего же для
разных пар наборов же может быть четыре случая: , , , .
a | b | c | d | F |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 0 | 1 | 1 |
0 | 0 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 1 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 1 |
Разместим на рабочей области новый мультиплексор, установим ему количество выбирающих (адресных) входов равным трем, и выполним необходимые соединения (рис. 3)

Рассмотрим реализацию заданной функции на минимальном количестве мультиплексоров 4-1.
Мультиплексор 4-1 имеет 2 адресных входа и 4 информационных. Это означает, что мы должны разбить исходную таблицу истинности на 4 фрагмента, за реализацию каждого из которых в принципе должен отвечать отдельный мультиплексор (назовем его операционным). Однако, необходимо учесть требования минимальности по отношению к количеству используемых мультиплексоров и ставить их только там, где без них нельзя обойтись. Также нам нельзя в рамках данной работы использовать другие логические схемы, за исключением отрицания.
По аналогии с реализацией на дешифраторах 2-4 (см. предыдущую работу), нам обязательно потребуется управляющий мультиплексор, который будет выбирать один из вариантов, предлагаемых операционными мультиплексорами (либо один из очевидных вариантов, если без операционных мультиплексоров можно обойтись).
Разобьем исходную таблицу истинности на зоны ответственности между операционными мультиплексорами, а заодно посмотрим, нельзя ли в некоторых случаях обойтись вообще без операционного мультиплексора (рис. 4).
Первый операционный мультиплексор работает, когда “ ab” равны 00
Второй, когда “ab” равны 01
Третий, когда “ab” равны 10
Четвертый, когда “ab” равны 11
Без первого можно обойтись , поскольку на данном фрагменте F=d
Второй операционный мультиплексор нужен
Третий операционный мультиплексор нужен
Четвертый операционный мультиплексор нужен
a | b | c | d | F |
0 | 0 | 0 | 0 | 1 |
0 | 0 | 0 | 1 | 0 |
0 | 0 | 1 | 0 | 1 |
0 | 0 | 1 | 1 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 0 | 1 | 1 |
0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 0 | 1 | 1 |
1 | 0 | 1 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 0 | 0 |
1 | 1 | 0 | 1 | 1 |
1 | 1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 | 0 |
Рис. 4 Разбиение исходной таблицы истинности на зоны ответственности для потенциальных операционных мультиплексоров
Как видно из рис. 3, в одном случае из четырех без операционного мультиплексора можно вполне обойтись. С учетом только что сказанного, схема логической функции на минимальном количестве мультиплексоров 4-1 будет такой, как показано на рис. 5

Реализуем логическую функцию, используя минимальную комбинацию мультиплексоров 4-1 и 2-1. В качестве отправной точки рассмотрим результаты, полученные в предыдущей реализации. Управляющий мультиплексор нельзя заменить на мультиплексор 2-1, поскольку у него на входах уникальные сигналы, а вот операционный заменить можно, поскольку он имеет дело с константами. Из рис. 4 выпишем отдельно фрагменты таблицы истинности, за который данные мультиплексоры отвечают (табл. 3,4,5).
Таблица 3
c | d | F |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Таблица 4
c | d | F |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Таблица 5
c | d | F |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 1 |
1 | 1 | 1 |

В результате получим схему, изображенную на рис.6.
В ходе лабораторной работы, я, Косенков Владислав Эдуардович, студент группы ИВБО-01-18 выполнил следующие задачи: восстановил таблицу истинности. По таблице истинности реализовал в лабораторном комплексе логическую функцию на мультиплексорах четырьмя способами:

Вы публикуете как гость. Если у вас есть аккаунт, авторизуйтесь, чтобы опубликовать от имени своего аккаунта.
Примечание: Ваш пост будет проверен модератором, прежде чем станет видимым.
Последние посетители 0 пользователей онлайн
Помогите подобрать микросхему, аналогичную по корпусу и разводке микросхемам TDA7297,TDA7266,TDA7377 но только с двухполярным напряжением питания.
Добрый день. Собираю зарядку по варианту Е, сейчас на стадии проектирования платы. В связи с маленьким размером корпуса, компоновка довольно плотная, поэтому обвязку TL94 делаю в СМД. Вопрос можно-ли применять керамические конденсаторы С2, С4, С5 и вместо электролитов С1 и С9 применить керамику, а вместо С16 тантал?


Похожий контент

Здраствуйте, учился создавать схемы на простой логике (хобби завел себе такое) и задался целью спроектировать эвм с собственными инструкциями.
Сделал, однако сейчас ломаю голову как ее воплотить в железо? Если кто может помочь в переводе схемы на реальный кремний или знает программы, куда я могу перенести или переписать свой эвм.
P.S. Проектировал в logisim.
P.P.S. Если кто может то подскажите что не так и как можно доработать схему. (она работает, но я любитель поэтому могу ошибаться).
Заранее благодарю за ответ.
компьютер один процесор.circ
Там простая схема. (в названии файла ошибка "процессор - алу")

В этой теме периодически буду предлагать компьютерное железо.
• 1.Офисная платформа LGA1155 (motherboard + CPU):
Asus P8H61 - MX (R2.0)
Intel Pentium G2020
Всё абсолютно исправно, планка I/O в комплекте, мало б/у, любые тесты по требованию, вплоть до видео, модуль DDR III 10600 2 GB и кулер (PWM) по желанию, отправка почтой или ТК ПЭК (предпочтительней) за счёт покупателя.
Ценник вижу в районе 5 000.
• 2.Gigabyte GTX650 1GDR5/128Bit, не играла, не майнила, не жарилась, не разбиралась, в полном порядке - 2 500
Обсуждаемо.

Приветствую, форумчане!
Перерыл весь интернет, информации по процу нет. Обращаюсь к вам за помощью, может у кого окажется.
Регистр, способный хранить один байт данных это уже неплохо, но как можно работать с более большими объемами информации? Для этого нам необходимо объединить несколько регистров в единую систему. Но помимо самих регистров в такой системе также должен присутствовать такой элемент как декодер. Сначала посмотрим на него в общих чертах.

Как видно, у него два входа и четыре выхода. Сходу кажется нелогичным. Давайте сначала вспомним, сколько комбинаций могут образовывать два бита? Четыре: 00, 01, 10, 11. То есть декодер на входе может иметь четыре возможные пары значений. Теперь посмотрим какой выход соответствует каждой из пар.

Как видно соблюдается следующий паттерн: на одном из выходов декодера всегда единица, а на остальных — ноль. На каком именно выходе будет единица, зависит от входа. То есть декодер так устроен, что каждой уникальной входной комбинации соответствует уникальная выходная комбинация. Поэтому, если декодер имеет два входа, он будет обязательно иметь четыре выхода.

Но декодер может принимать и больше входных значений. Например, три. Но три бита могут образовывать уже 8 комбинаций, поэтому в таком случае декодер должен иметь и восемь выходов. Если четыре входа, то 16 выходов и т.д.
Построение декодера

Теперь, построим такую штуку из логических элементов. Сначала для простоты начнем с декодера 2×4.
Итак, мы видим четыре провода. Значения, которые имеют первые два (A и B) задаются нами, значения notA и notB представляют собой отрицания значений A и B. Всего эти четыре провода могут нести четыре уникальных комбинаций.

0

Можно заметить, что в любой из возможных комбинаций два каких-либо провода всегда несут единицы, а два других всегда ноль. Используем это свойство для построения декодера. Применим логический гейт AND, который выдает единицу только когда на всех его входах подаются единицы.
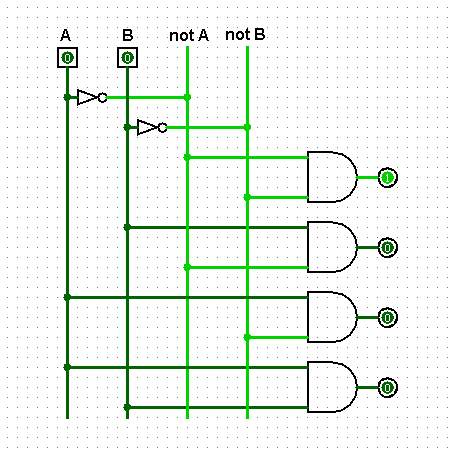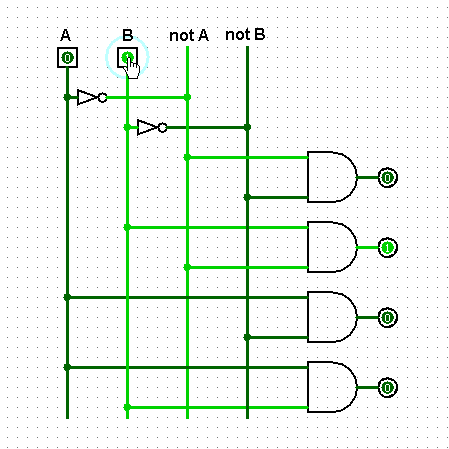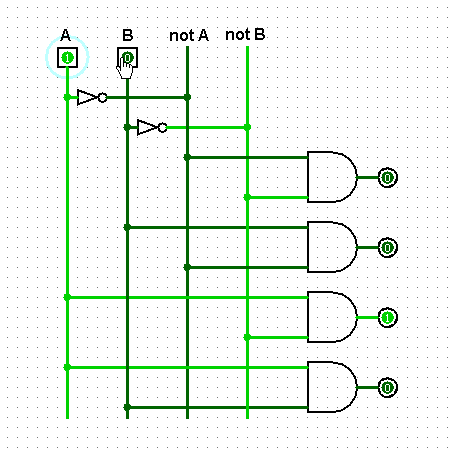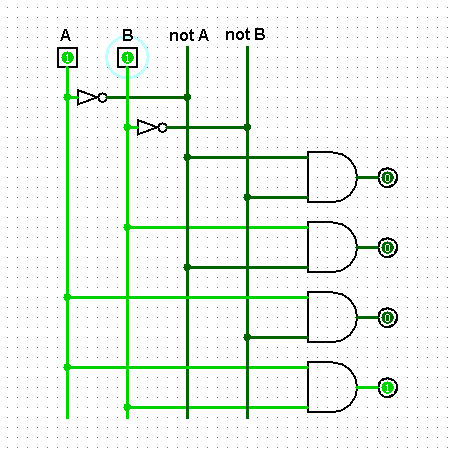
Итак, когда два каких-либо провода несут единицы они также передают эти единицы определенному AND-гейту и следовательно этот гейт на выходе будет иметь единицу. Другие же AND-гейты выдают в это время ноль, поскольку либо на одном либо на обоих проводах, с которых они берут входящие значения, будет присутствовать ноль.

Основываясь на этом же принципе можно построить декодер 3×8, но для этого нам также потребуется AND-гейт с тремя входами.
Смысл его работы такой же: он выдает единицу только, когда на всех (трех) его входах единицы, а в остальных случаях он выдает ноль.

Теперь посмотрим на декодер 3×8

Его отличие от предыдущего в том, что в нем три провода всегда будут нести единицу, а три других всегда ноль. Поэтому мы используем AND-гейт с тремя входами.

По такому же принципу работает декодер 4×16, который мы будем использовать в схеме оперативной памяти.
Структура оперативной памяти

Представим, что у нас есть 16 ячеек памяти по одному байту. Как нам с ними работать? Сначала сгруппируем их в виде таблицы 4×4. Потом добавим к каждой из низ два входа (горизонтальный и вертикальный). Потом берем два декодера 2×4 и подключаем их таким образом. Сами декодеры получает свои значения из блока памяти размером 4 бита.
Ячейка памяти

Сразу перейдем к схеме.
Читайте также:


