Как сделать многогранники тела вращения

Тип урока: изучение нового материала, практическая работа.
Метод урока: частично - поисковый.
Оборудование: геометрические тела, чертежные принадлежности, инструкционная карта, карточки задания.
Ход урока: І. Организационная часть.
Проверка готовности учащихся к уроку,
психологический настрой к учебной деятельности.
- Я в школе на уроке.
Сейчас я начну учиться.
Я радуюсь этому.
Внимание моё растет.
Я, как разведчик, все замечу.
Память моя крепка.
Голова мыслит ясно.
Я готов к работе.
- Ну что, настроились на урок, тогда начнем. Давайте повторим то что мы проходили на предыдущих уроках.
ІІ.Связь с педыдущими уроками.
* Какие бывают карандаши?
* Как определить твердость или мягкость карандаша?
* Как правильно затачивают карандаши?
* С какого карандаша начинаем чертеж?
3. Прямоугольник с ровными сторонами.
4. Один из самых необходимых инструментов для выполнения чертежа
1. Основной конструкторский документ.
2. Стержень карандаша.
3. Сторона в прямоугольном треугольнике.
3. Карточки- задания "Линий чертежей"
ІІІ.Формирование новых знаний и понятий.
Учитель: Ребята, посмотрите на разнообразные хорошо вам известные предметы, представленные на нашей выставке. Это геометрические тела. На какие части делятся геометрические тела? ( на многогранники и тела вращения). Давайте назовем их. ( ученики по очереди называют предметы).
Учитель: Посмотрите на эти геометрические тела внимательно, подумайте, что в них общего? ( Все предметы изготовлены из материала маленькой толщины и получены путем сгибания, сворачивания).
Как бы вы изготовили вот такую коробочку? ( путем вычерчивания по размерам; использования путем разворота образца как выкроику, которую надо вырезать из картона а затем ее согнуть). А как по- другому можно назвать выкройку? ( Развертка). Вот мы и определили тему нашего урока. Запишите ее в тетрадь.
Итак, ребята из объемного пространственного тела мы получили на плоскости что? ( фигуру). Попробуйте дать определение развертке. Что называется разверткой? (Разверткой называется плоская фигура, полученная путем соединения всех граней с плоскостью).
Развертка поверхности шестиугольной призмы.
Полная поверхность призмы состоит из боковой поверхности и двух равных основании (верхнего и нижнего). Боковая поверхность шестиугольной призмы состоит из шести прямоугольников с основанием равным, стороне правильного шестиугольника, и высотой, равной высоте призмы. Для получения полной развертки призмы необходимо к развертке боковой поверхности пристроить верхнее и нижнее основания. Таким же образом поступают треугольной призмой. ( Рисунок 1, рисунок 2, рисунок 3, рисунок 4, рисунок 5)
І? Практическая работа.
Выполнение развертки куба. ( по инструкционной карте).
? Проверка работ учащихся.
Самооценка учащихся с помощью фишек ( зеленная - 5, синяя -4, красная - 3).
?І. Рефлексия
Чемодан, мясорубка,корзина.
На доске вывешиваются рисунки чемодана, мясорубки, корзины.
Чемодан – всё, что пригодится в дальнейшем.
Мясорубка – информацию переработаю.
Корзина – всё выброшу.
Ученикам предлагается выбрать, как они поступят с информацией, полученной на уроке.
Д/З: Творческое задание - изготовить из бумаги необычный предмет, поделку, используя развертки геометрических тел (демонстрация примеров творческих работ).
Тема урока: Развертки геометрических тел.
Цель урока: 1.Формирование новых знаний и понятий, формирование
умений выполнять развертки геометрических тел.
2.Развитие пространственных представлений и
3.Воспитание аккуратности, внимательности, дисциплине
Тип урока: изучение нового материала, практическая работа.
Метод урока: частично - поисковый.
Оборудование: геометрические тела, чертежные принадлежности, инструкционная карта, карточки задания.
Ход урока: І. Организационная часть.
Проверка готовности учащихся к уроку,
психологический настрой к учебной деятельности.
- Я в школе на уроке.
Сейчас я начну учиться.
Я радуюсь этому.
Внимание моё растет.
Я, как разведчик, все замечу.
Память моя крепка.
Голова мыслит ясно.
Я готов к работе.
- Ну что, настроились на урок, тогда начнем. Давайте повторим то что мы проходили на предыдущих уроках.
ІІ.Связь с педыдущими уроками.
* Какие бывают карандаши? * Как определить твердость или мягкость карандаша? * Как правильно затачивают карандаши?
* С какого карандаша начинаем чертеж?
3. Прямоугольник с ровными сторонами.
4. Один из самых необходимых инструментов для выполнения чертежа
1. Основной конструкторский документ.
2. Стержень карандаша.
3. Сторона в прямоугольном треугольнике.
3. Карточки- задания "Линий чертежей"
ІІІ.Формирование новых знаний и понятий.
Учитель: Ребята, посмотрите на разнообразные хорошо вам известные предметы, представленные на нашей выставке. Это геометрические тела. На какие части делятся геометрические тела? ( на многогранники и тела вращения). Давайте назовем их. ( ученики по очереди называют предметы).
Учитель: Посмотрите на эти геометрические тела внимательно, подумайте, что в них общего? ( Все предметы изготовлены из материала маленькой толщины и получены путем сгибания, сворачивания). Как бы вы изготовили вот такую коробочку? ( путем вычерчивания по размерам; использования путем разворота образца как выкроику, которую надо вырезать из картона а затем ее согнуть). А как по- другому можно назвать выкройку? ( Развертка). Вот мы и определили тему нашего урока. Запишите ее в тетрадь.
Итак, ребята из объемного пространственного тела мы получили на плоскости что? ( фигуру). Попробуйте дать определение развертке. Что называется разверткой? (Разверткой называется плоская фигура, полученная путем соединения всех граней с плоскостью).
Развертка поверхности шестиугольной призмы.
Полная поверхность призмы состоит из боковой поверхности и двух равных основании (верхнего и нижнего). Боковая поверхность шестиугольной призмы состоит из шести прямоугольников с основанием равным, стороне правильного шестиугольника, и высотой, равной высоте призмы. Для получения полной развертки призмы необходимо к развертке боковой поверхности пристроить верхнее и нижнее основания. Таким же образом поступают треугольной призмой. ( Рисунок 1, рисунок 2, рисунок 3, рисунок 4, рисунок 5)
ІҮ Практическая работа.
Выполнение развертки куба. ( по инструкционной карте).
Ү Проверка работ учащихся. Самооценка учащихся с помощью фишек ( зеленная - 5, синяя -4, красная - 3).
ҮІ. Рефлексия
Чемодан, мясорубка,корзина.
На доске вывешиваются рисунки чемодана, мясорубки, корзины.
Чемодан – всё, что пригодится в дальнейшем.
Мясорубка – информацию переработаю.
Корзина – всё выброшу.
Ученикам предлагается выбрать, как они поступят с информацией, полученной на уроке.
Д/З: Творческое задание - изготовить из бумаги необычный предмет, поделку, используя развертки геометрических тел (демонстрация примеров творческих работ).
Большой выбор развёрток простых геометрических фигур.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров :)

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

Довольно интересная фигура – ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
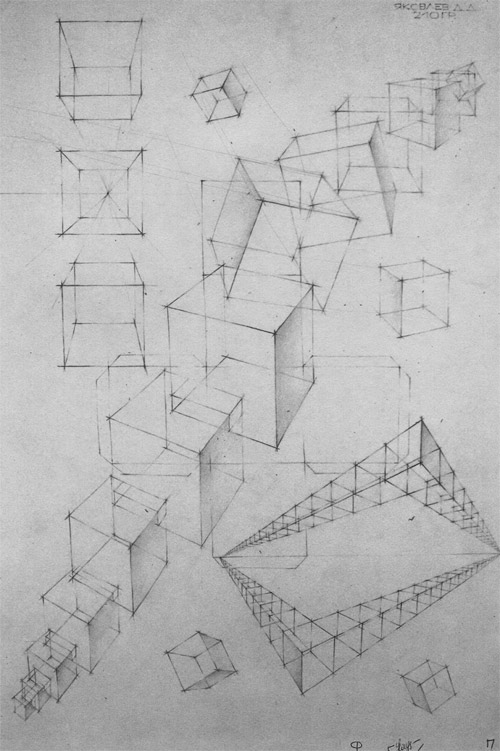
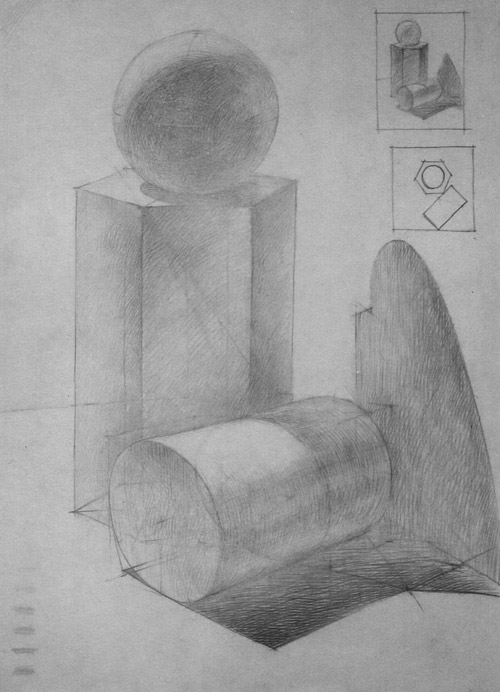
На рисунке приведены примеры выполнения рисунка многогранников. Рисовать их необходимо в следующей последовательности. Во-первых, надо установить положение многогранника в пространстве относительно рисующего. Если многогранник расположен фронтально, то следует переднюю грань рисовать без искажений и использовать одну точку схода. Следует строго соблюдать вертикальность и горизонтальность ребер. Проверять себя лучше всего, сравнивая нарисованные линии с краями листа бумаги.
Если многогранник расположен к рисующему углом, то и рисовать его надо с ближайшего угла. Намечаем вертикальное ближнее ребро и сами задаем его размер. Затем находим углы наклона ребер основания. Эти наклонные линии находим по отношению к горизонтальной линии, сравнивая их между собой. Только после этого находим степень сокращенности боковых граней относительно размера вертикального ребра и сравниваем их горизонтальные размеры между собой.
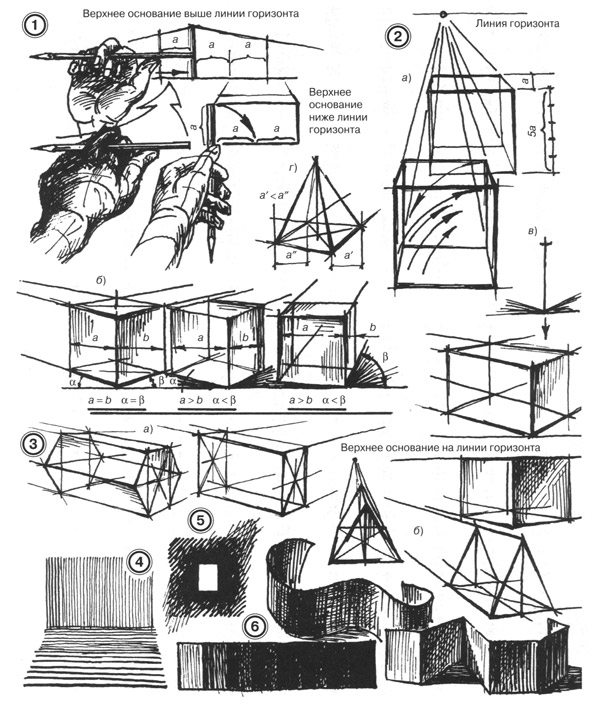
Главные задачи для рисующего:
- добиться впечатления в изображении той фигуры, которую рисуешь;
- твердо поставить ее на горизонтальную плоскость;
- правильно изобразить перспективные сокращения граней и ребер.
Рисовать обязательно прозрачно, а линии построения продолжать несколько дальше контуров предмета. Углы нижнего основания и размеры ширины боковых плоскостей взаимосвязаны и зависят от точки зрения наблюдателя. Если рисующий установил, что видимые ребра куба имеют у основания одинаковые углы, то боковые грани он может изображать с одинаковыми сокращениями. Чем сильнее сокращается грань, тем круче угол подъема ребра основания.
1 — метод визирования;
2 — рисование многогранников: а — куб во фронтальном положении, б — куб под углом, е — последовательность рисования фигуры под углом; г — построение пирамиды с квадратным основанием;
3 — последовательность работы над рисунком шестиугольной призмы (а), линейно-конструктивные рисунки треугольной призмы (б);
4 — методы штриховки вертикальных и горизонтальных плоскостей;
5 — краевой контраст: усиление тона штрихом, наслаивающимся на предыдущий;
6 — упражнения на плавное и ступенчатое усиление тона; тональный масштаб; упражнения на усиление тона от светлого к темному.
Прежде чем переходить к светотеневому рисунку, необходимо освоить приемы штрихования поверхностей.
Выполняя эти упражнения, рисующий должен:
- штрихи наносить, свободно двигая кистью руки в разных направлениях;
- стараться не отрывать грифель карандаша от плоскости рисунка;
- усиливая тон, не нажимать на карандаш, а накладывать новый ряд штрихов в том же направлении или под другим углом.
Рекомендуем упражнения на шриховку начинать с изображения вертикальных и горизонтальных плоскостей, вначале покрывая их равномерным тоном, а затем выявлять пространственные отношения, усиливая тон ближних планов. Далее нужно проработать приемы штриховки с тоновыми градациями от светлого к темному с плавным и ступенчатым переходами.
Завершить эту группу упражнений желательно тренировкой глаза на различие наибольшего количества тоновых градаций. Выполняя это упражнение, вы подводите себя к понятию тонального масштаба.
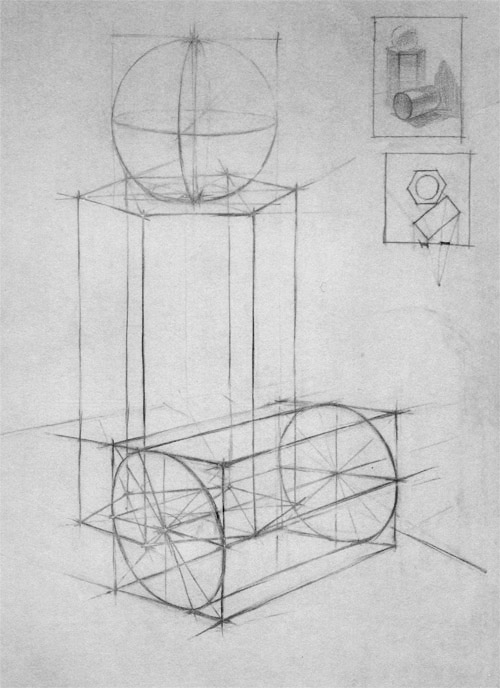
Изображение тел вращения
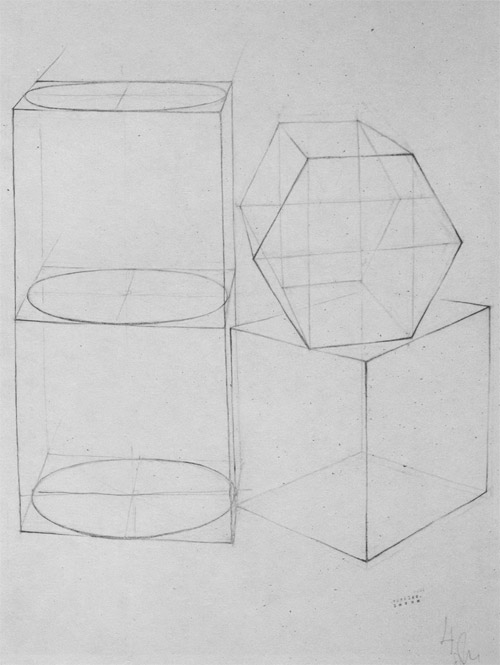
Прежде чем выполнять рисунки тел вращения, необходимо научиться рисовать круг в перспективе. На рисунке дана последовательность изображения фигуры, напоминающей форму эллипса, в горизонтальной и вертикальной плоскостях. Эта замкнутая фигура строится на двух взаимно перпендикулярных осях (малой и большой), которые вначале и намечают в рисунке. Далее прорисовывают боковые закругления, а уже потом рисуют фигуру целиком. В зависимости от линии горизонта ширина эллипса изменяется, а длина остается прежней. Для более точного изображения этой фигуры ее можно заключить в квадрат.
На рисунке приводится последовательность работы над рисунком тел вращения. Главная задача рисующего при построении оснований состоит в том, чтобы большая ось эллипса была перпендикулярна центральной оси тела вращения. Необходимо проследить также, чтобы основание предмета твердо стояло на горизонтальной плоскости и было изображено с учетом удаленности от линии глаз рисующего, и строго соблюдать пропорции общей формы и отдельных частей.
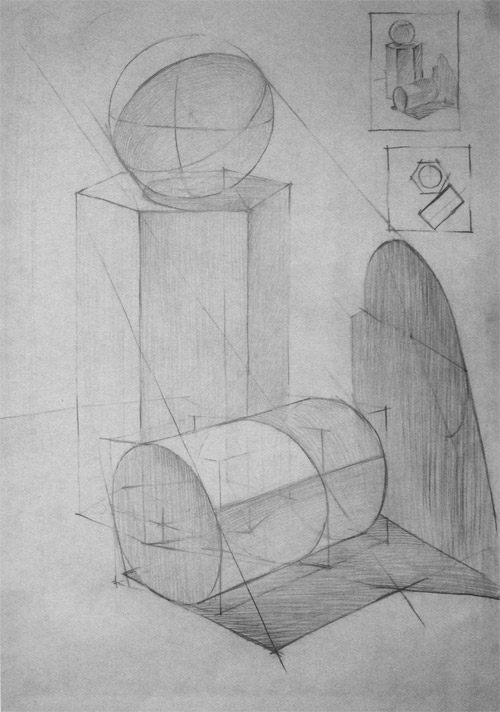
Линейно-конструктивный рисунок не заканчивается на построении контуров фигуры. Следует построить границы собственных и падающих теней. Строить тени в рисунке нужно визуально, но учитывая при этом источник света. Изображая собственные тени многогранников, следует помнить, что каждая грань отличается по тону. Внутри тень на гипсовых телах имеет различные тоновые градации. На ребрах, граничащих со светом, накапливается более темный тон.
Тела вращения имеют собственные тени с мягкими переходами тоновых градаций. Следует отметить, что лучи света, которые падают на поверхность гипсовой фигуры под прямым углом, делают ее самой светлой. Лучи света, скользящие по поверхности под углом, создают более затемненные места. Наконец, лучи не попадающие на поверхность, образуют глубокие тени. Отраженные от других поверхностей лучи, попадая в глубокую тень, высвечивают некоторые участки (рефлексы). Рефлексы всегда темнее освещенных мест предмета.
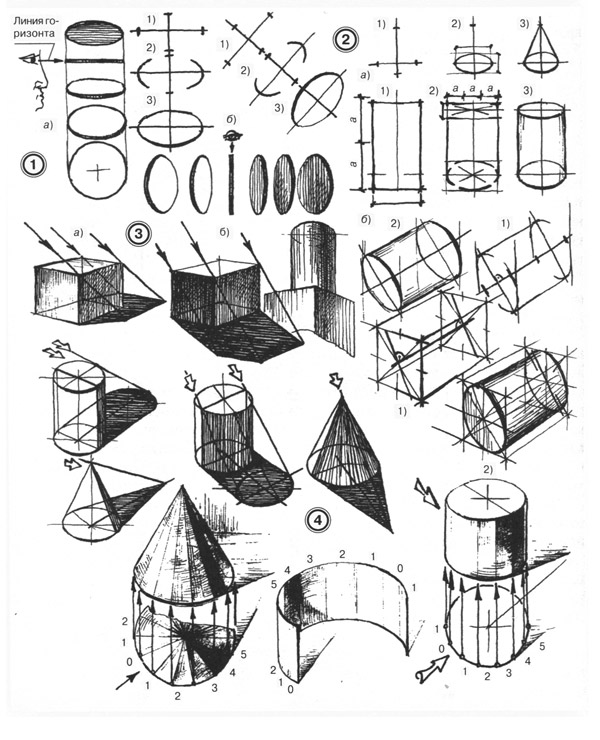
1 — изображение окружности в перспективе: а — изменение размеров эллипса при удалении от линии горизонта и точки зрения, б — последовательность построения эллипса;
2 — последовательность работы над рисунком тел вращения: а — построение конуса, б — два способа построения цилиндра;
3 — некоторые закономерности построения теней: а — источник света слева спереди, б — источник света сзади объекта;
4 — градации тона и фазы светотени на телах вращения: 0 —самое светлое место (блик), 1 — свет, 2 — полусвет, 3 — полутень, 4 — тень, 5 — рефлекс.
Конечно, слепо копировать различную технику не следует. Богатая техника вырабатывается только путем самостоятельного рисования с натуры. Надо искать свои приемы, которые бы отвечали собственному восприятию натуры.

Многогранники и тела вращения имеют красивые формы, например, правильные, звездчатые многогранники, тор. Они обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед, Платон, Аполлоний Пергский.
Названия правильных многогранников появились в Древней Греции, в них определяется число граней: " тетраэдр " - четырехгранник; " гексаэдр " - шестигранник; " октаэдр " - восьмигранник; " икосаэдр " - двадцатигранник; " додекаэдр " - двенадцатигранник. Платоновы тела или правильные многогранники являются уникальными геометрическими объектами, с ними связывали свое представление о гармонии Мироздания [10].
Первичные данные о свойствах тел вращения характерны к времени зарождения геометрии как дальнейшей математической науки. Строгие доказательства теорем, служащих для вывода формул тел вращения изложены в книге “Начал” Евклида. Труды Евклида и Архимеда после их перевода на арабский язык, а с арабского на латинский пробираются в Европу и формируют основу для составления учебников и книг для средних школ.
Актуальность нашего исследования состоит в том, что решение задач способствует развитию пространственных представлений, умения логически мыслить, углубляет и расширяет курс геометрии и показывает практическое применение геометрических знаний в реальной жизни . Тема "Комбинации геометрических тел" рассматривается как завершающая после повторения свойств многогранников и тел вращения. При решении задач на комбинации геометрических тел, кроме традиционных методов с использованием алгебры и тригонометрии, применяются и другие методы, например, векторный.
Комбинации геометрических тел — одна из самых трудных тем геометрии . Решение стереометрической задачи то и дело приводит к решению планиметрических задач, поэтому приходится возвращаться к планиметрии, основным определениям, теоремам, формулам, необходимые для решения данных задач. Поэтому именно задачи на комбинации геометрических тел были широко представлены среди геометрических задач повышенной трудности в ЕГЭ по профильной математике [21].
В нашей жизни мы часто встречаем предметы, которые строятся на базе определенных геометрических фигур либо на их комбинации. Данная тема имеет яркие приложения. Леонардо да Винчи , в частности , воодушевился теорией многогранников и нередко представлял их на своих картинах , а в архитектуре самые распространённые многогранники — прямые призмы.
Объект исследования : раздел элементарной математики, связанный с многогранниками и телами вращения.
Предмет исследования: методы и приемы решения задач на комбинацию многогранников и тел вращения.
Цель исследования: систематизация теоретического материала по теме
" Комбинации многогранников и тел вращения " и его применение к решению задач.
Задачи исследования:
Знакомство с историей возникновения многогранников и тел вращения.
Изучить теоретические положения, связанные с многранниками, телами вращения и комбинациями геометрических тел.
Рассмотреть решения задач на комбинацию многогранников и тел вращения.
Результаты исследования были представлены на конференциях:
Работа состоит из введения, двух глав и заключения. Список использованной литературы включает 23 наименований.
Глава I . Комбинации многогранников и тел вращения
Исторические сведения
Начальные сведения о свойствах геометрических тел люди обнаружили, рассматривая окружающий мир и в результате практической деятельности. За период с VII по III век до нашей эры греческие геометры не только пополнили геометрию многочисленными новыми теоремами, но сделали также значительные шаги к строгому ее обоснованию.
Особое внимание было к правильным многоугольникам и правильным многогранникам, которые с глубокой древности считались символами совершенства и красоты. Правильные многоугольники можно объединять в плоские фигуры, а также и в пространственные фигуры.
Известно еще множество совершенных тел, получивших название полуправильных многогранников или Архимедовых тел. Существует 13 полуправильных многогранников, открытие которых приписывается Архимеду. Множество Архимедовых тел можно разделить на несколько групп. Первую из них формируют пять многогранников, которые получаются из Платоновых тел в результате их усечения. Для Платоновых тел усечение может быть сделано таким образом, что и образующиеся новые грани, и остающиеся части прежних будут правильными многоугольниками. Таким путем могут быть получены пять Архимедовых тел [5].
Изучением звёздчатых многогранников занимались различные математики в разные времена. Их всегда привлекали особенные свойства симметрии, а также они считались символом красоты и совершенства. В 1811 году было установлено, что существуют всего 4 правильных звёздчатых тела Огюстеном Лу Коши. При этом они не являются соединениями Платоновых и звёздчатых тел. Отсюда и пошли звёздочные тела Кеплера — Пуансо. В 1619 году Иоганн Кеплер открыл малый звёздчатый додекаэдр и большой звёздчатый додекаэдр, а в 1809 году Луи Пуансо открыл большой додекаэдр и большой икосаэдр. Оставшиеся правильные звёздчатые многогранники являются соединениями Платоновых тел или соединениями тел Кеплера — Пуансо [7].
Вывод: В первом параграфе рассмотрена историческая справка о геометрических телах.
Общие сведения о многогранниках
Пространственные фигуры, изучаемые в стереометрии, называют телами или геометрическими телами. Наглядно тело надо представлять себе как часть пространства, занятую физическим телом и ограниченную поверхностью.
Определение 1. Многогранник — геометрическое тело, поверхность которого состоит из конечного числа плоских многоугольников.
Многогранник называется выпуклым , если он расположен по одну сторону плоскости каждого плоского многоугольника на его поверхности. Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника являются плоскими выпуклыми многоугольниками. Стороны граней называются ребрами многогранника, а вершины — вершинами многогранника.
Определение 2. Призма — многогранник, состоящий из плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.
1. Основания призмы равны.
2. Основания призмы лежат в параллельных плоскостях.
З. Боковые ребра параллельны и равны.
4. Боковые грани — параллелограммы.
Определение 3. Пирамида — многогранник, основание которого является многоугольник, а остальные грани — треугольники, имеющие общую вершину.
1. Боковые ребра равны, одинаково наклонены к плоскости основания.
2. Боковые грани — равные друг другу равнобедренные треугольники.
3. Апофемы равны и наклонены к плоскости основания под одним углом.
Определение 4. Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.
Свойства усеченной пирамиды:
Каждая боковая грань усеченной пирамиды является равнобокими трапециями одной величины.
Основания усеченной пирамиды являются подобными многоугольниками.
Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
Боковые грани усеченной пирамиды являются трапециями.
Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.
В таблице 1 показаны формулы, которые будут необходимы при решении задач на данную тему [12] .
Вывод: Во втором параграфе рассмотрены геометрические определения о многогранниках.
Читайте также:


