Как сделать минусовую степень в паскале
Репутация: 55
В FAQ рассмотрено возведение в целую степень отрицательных чисел.. А как быть с вещественными степенями?
Даже если в случае получения комплексного результата писать "ошибка" (ну типа по-школьному: из отрицательных чисел квадратный корень не извлекается).
Если говорить о степени, представленной в виде a/b, где a и b целые, то особых проблем нет: смотрим на четность b и делаем вывод о возможности вычислений, четность а даст знак. (ну например (-1)^(1/3)=-1, (-1)^(2/3)=1).
Но как к этому прийти, если есть число - конечная за счет ограниченности разрядной сетки десятичная дробь?
Рассматривать 1.234 как 1234/1000? А дальше - пытаться сократить и смотреть на четность? Бред какой-то.
MathCad ответа не дал: у него все просто (-1)^0.5=-1 (при этом корень из -1 равен i )
Репутация: 32
Репутация: 3
Репутация: 32
Репутация: 3
Репутация: 11
Если я не ошибаюсь, то рациональное число можно представить в виде дроби. Вот и определяй новый тип данных, дописывай новое определение функции возведения в степень, ну можно и перезагрузкой операторов заняться. Только ради чего это нужно?
Репутация: 32
Вот я тут придумал прикольный пример.
Если мы хотим ввести операцию возведения отрицательного числа хотя бы в рациональную степень, естественно ожидать от нее некоторого привычного поведения.
С одной стороны, (-1)^3 = -1 * -1 * -1 = -1
С другой, воспользуемся формулой a^(xy) = (a^x)^y:
(-1)^3 = (-1)^(2 * 1.5) = ((-1) ^ 2) ^ 1.5 = 1 ^ 1.5 = 1
Таким образом, даже не допуская в вычислениях непосредственного возведения отрицательных чисел в дробную степень, получаем противоречие.
Репутация: 55
ну вот.. совсем интересно получается
и не скажешь, что формула справедлива только для целых х,у:
(-1)^(2/3)=((-1)^(1/3))^2 (ну и в другом порядке то же самое.
в общем, запуталась
Репутация: 32
Репутация: 55
То есть ловить ситуации, когда вещественное число по сути целое (MathCad даже это игнорирует: -1^4.0=-1, -1^4=1) с какой-то точностью.. и все?
Репутация: 32
Ну наверное, да. Только это от того зависит, зачем это тебе. Я бы вообще запретил такое, если б, скажем, консоль какую-то писал.
Репутация: 55
Вообще-то это было задание сестры моей подруги. Учится она на первом курсе, специальность с ходу не назову. но что-то гуманитарное. Звучит в оригинале так:
Написать функцию для вычисления вещественной степени вещественного числа, а также основную программу, вызывающую эту подпрограмму.
При том, что остальные задания на уровне "найти максимум в одномерном массиве".
Видимо, просто не совсем корректная формулировка.
Репутация: 0
Стоп, написать эту функию на Паскале - нет проблем.
Репутация: 55
Репутация: 0
Ещё раз стоп. Отрицательного числа в вещественной степени не существует. Может в мнимых числах что-то и будет, но согласись: нелогично давать задачу, в которой входные данные - вещественные, а результат - то вещественный, то комплексный (то есть два вещественных числа). Да ещё и на первом курсе гуманитарного ВУЗа. Нет, не верю я в это.
P.S. Если я что-то не то сказал про мнимые числа, то, математики, поправте.
Репутация: 55
Даже если в случае получения комплексного результата писать "ошибка" (ну типа по-школьному: из отрицательных чисел квадратный корень не извлекается).
в общем, про (A^B)=exp(B*ln(A)) ты абсолютно не в тему написал. вопрос изначально был только про отрицательные числа.
И еще раз перечитай тему с самого начала. (-2) 2 тебе кто-то запретил делать? Нет. А теперь к результату применить res 1/3 Соображаешь? А ты говоришь, комплексные. Тебе результат показать, или сам посчитаешь? А что это, как не (-2) 2/3 .
Репутация: 32
Репутация: 159
Чего нету, того нету..
Доопределение операции возведения в степень на вещественные числа для отрицательных чисел по непрерывности произвести невозможно. И комплексные числу тут не помогут! Более того, даже (как заметила мисс_граффити еще в самом первом мессадже) для рациональных невозможно, не то что иррациональных. Пример Michael_Rybak неплох, но вот гляньте сюда:
-3 = (-3)^1 = (-3)^(2/2) = Sqrt((-3)^2) = |-3| = 3
Неплохой пример софистики, а? Кстати, как-то была такая тема..
Иными словами, область определения операции возведения в степень - это x>0. Можно считать, что это "по-школьному", а можно говорить, что Истина открылась еще на школьной скамье..
И даже для целых степеней, строго говоря, эта операция с отрицательным основанием некорректна. То есть ее можно рассматривать только не более, чем сокращение записи x*x*x*. *x (умножение n раз), как это, собственно, и было при введении степени. Но для положительных оснований это удалось расширить и довести до статуса операции, а для отрицательных оно так и осталось - сокращенная запись для многократного умножения..
Так что если вам предложат задачу, где в качестве основания стоит отрицательное число - считайте, что вам повезло. Решение этой задачи закончится, не начавшись..
Репутация: 55
Недавно обнаружил, что многие не знают, как возвести число в некоторую степень.
Самый легкий способ просто перемножать это число в цикле, т.к в паскале нет специальной функции возведения числа в степень.
Код:
st := 10;
rez := 1;
For i := 1 to st do
rez := rez * chislo;
st - необходимая степень,
chislo - данное число,
rez - результат.
Есть и другой вариант возведения, более быстрый с возможностью возведения в большую степень очень большого числа . Но об этом расскажу позже.
Чебурашка Активный пользователь
автор Чебурашка Сб Июл 03, 2010 2:31 am
По твоему примеру можно и назад считать!))
ВОт мой небольшой алгоритм
Код: k := n;
b := 1;
c := a;
while k <> 0 do begin
if k mod 2 = 0 then begin
k:= k div 2;
c:= c * c;
end else begin
k := k - 1;
b := b * c;
end;
end;
Нередко мы сталкиваемся с тем, что нам необходимо возвести число в какую-либо степень. Можно воспользоваться обычным калькулятором. Но это неинтересно и очень часто не подходит под условия поставленной задачи.
Понятие степени в математике
Стоит начать с пояснения математического смысла возведения в степень. Например, нам необходимо возвести некоторое число x в степень y. В математике эта запись выглядела бы так: x y = x ^ y. Это означает, что число x нужно умножить на себя y раз. Помните: какое бы вы число ни возводили в нулевую степень, получится единица, а также при возведении в первую степень мы получим наше исходное число. При возведении в отрицательную степень мы всего лишь переворачиваем полученный результат.
Возведение в степень на паскале
С математикой всё понятно. Но как же нам сделать такую программу, которая будет производить возведение в степень? Тут всё просто. Если нам необходимо возвести x в степень 5, то наш код примет вид: res:= x * x * x * x * x. Мы умножили число x на себя 5 раз, как нам и было необходимо, но что делать, если нам не известна степень, в которую необходимо возвести число? Далее мы рассмотрим, как производить возведение в степень. Паскаль предоставляет нам не очень много возможностей для этого, но мы обязательно что-нибудь придумаем. Например, использование стандартных функций и процедур или использование различных циклов.
Возведение числа в квадрат
Начнём, пожалуй, с возведения в квадрат. Возведение в квадрат является частным случаем возведения в степень. Для этого в паскале предусмотрена стандартная процедура sqr(x). Она возведёт наше число x в квадрат, эта запись равна записи x*x.

Очень часто этого вполне достаточно, но не всегда программа может ограничиться одним лишь возведением в квадрат. Как же возводить в более высокие степени? Об этом читаем далее и просвещаемся.
Использование стандартных операторов
В паскале существует два метода для возведения числа в степень: exp(ln(x)*y) и метод power(x, y). Процедура exp() имеет ограничение: x должно быть больше 0, т.к. нельзя извлечь натуральный логарифм из неположительного числа, но эта функция считается устаревшей и неудобной для использования, поэтому дальше мы о ней говорить не будем. Функция power() принимает два значения, первое число (x) - которое нужно возвести в степень, второе число (y) - степень, в которую нужно возвести и возвращает x в степени y. Следует помнить, что числа х и у - вещественные, то есть типа real.

Но тут есть один недостаток, эта функция есть не во всех версиях паскаля. Да и вообще, иногда возведение в степень должно производиться без использования операторов. Идём дальше и разбираем следующий способ.
Возведение в степень при помощи цикла for
Как мы уже поняли, возведение числа в степень - это последовательное умножение числа на само себя несколько раз. Повторить какое-то действие несколько раз в программировании гораздо легче, чем в жизни. Воспользуемся циклом for:

Разберемся, что и как тут работает. Для начала мы вводим два числа: x и y. Затем берём за результат единицу, для чего это - ниже. Выполняем цикл до модуля нашей степени, т.к. если степень будет отрицательной, то цикл не пойдёт. В цикле мы умножаем наш результат на само число x. Так зачем мы присваивали результату 1? Во-первых, если бы мы умножали на 0, то программа всегда выдавала бы 0. Во-вторых, наша степень может быть равна 0, тогда программа должна вернуть нам 1, т.к. любое число в 0 степени это 1. Затем мы проверяем, является степень отрицательным числом или положительным: если она отрицательна, то делим единицу на наш результат. Выполнение этой задачи при помощи цикла while делается почти так же.
Использование цикла while при возведении в степень
Использование цикла while более правильно, нежели for, но для понимания проще предыдущий вариант. Вряд ли можно стоит ограничиваться одним лишь циклом for, для понимания будет лучше посмотреть несколько примеров, да и задача бывает поставлена по-разному, кому-то одним циклом, кому-то другим, именно поэтому мы разберём ещё один способ возведения в степень.

Всё почти так же, как и раньше. Вводим два числа х и у. Присваиваем нашему результату значение единицы, чтобы возводить в нулевую степень. Затем создаём счётчик i и присваиваем ему значение модуля нашей степени. Цикл идёт до тех пор, пока счётчик не равен нулю, если степень с самого начала равна нулю, то цикл не будет выполняться, результат так и останется единицей, как и должно быть, ведь любое число в нулевой степени - это единица. В самом цикле мы всё так же считаем результат, умножая уже полученный результат на наше число х, не забываем вычитать из нашего счётчика единицу, иначе мы никогда не дойдём до нуля. Ну а затем так же, как выше, преобразование, если степень была отрицательной. Ничего сложного, как оказалось. Впрочем, никто и не сомневался.
Что же, с обычными числами мы закончили, но ведь есть не только такие числа.
Понятие комплексных чисел
Нам с самого начала школьного обучения объясняют только обычные числа, но есть ведь ещё и другие, например, комплексные числа. Они довольно сложны в представлении, особенно учитывая то, что нас почти нигде не знакомят с ними. В математической записи они имеют вид z = x + yi, где x и y - это некоторые числа, а i - мысленная единица. Вы сразу подумали: да это же обычное число, стоит просто провести операцию сложения. Но нет, не всё так просто. Это не сумма, это именно число. Другими словами, если попытаться представить это всё с точки зрения геометрии, то можно заменить знак сложения точкой с запятой, и получатся как бы координаты точки, x и y. И если построить нулевой вектор до этой точки, то мы сможем визуально увидеть всё это. Кажется, текста стало слишком много, давайте немного посмотрим:
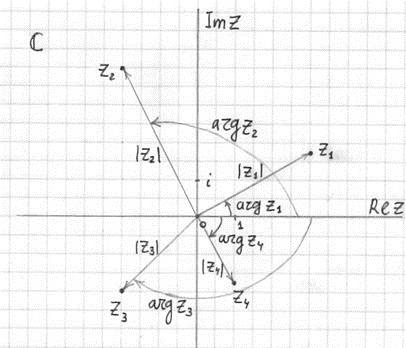
Если мы хотим показать, что наша плоскость комплексная, достаточно пометить её жирной буквой C, как тут. Затем мы можем видеть множество точек, давайте посмотрим на них и попытаемся понять, какая из них как записывается. Берём точку z1, опускаем проекцию на ось ReZ и получаем 3, затем на ось lmZ и получаем 1,75, в итоге имеем число z1=3 + 1.75i. Вроде всё понятно, давайте ещё раз, для закрепления. Точка z2, по горизонтальной оси - два, по вертикальной - четыре, в итоге имеем: z2=2 + 4i. Всё предельно понятно и просто.
С комплексными числами возможны все те же операции, что и с обычными. Сложение, вычитание, умножение, деление. Но в этой статье мы подробно остановимся на возведении комплексного числа в степень.
Возведение в степень комплексного числа
Что делать, если нужно возвести в степень комплексное число? Не паникуйте! Всё точно так же, как с обычными числами, но чуточку сложнее. Начнём с квадрата. Дано число z = 2 + 5i. Возводим в квадрат, получаем z 2 = (2 + 5i) 2 = (2 + 5i)(2 + 5i) - а это обычный двучлен, можно просто перемножить, привести подобные слагаемые и всё. Это очень просто, но что делать, когда нужно возвести в более высокую степень? Для начала следует представить наше число в тригонометрической форме, например:
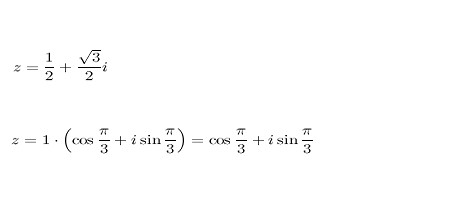
Затем необходимо воспользоваться формулой возведения комплексных чисел в тригонометрической форме: z n =|z| n * (cos(nx) + i * sin(nx)). Можно заметить, что при возведении комплексных чисел даже в очень большие степени они сильно не изменяются, так что не пугайтесь, это сложно, но с практикой всё придёт.
Таким образом, теперь вы знаете, как возводить числа в степень в математике, на языке программирования паскаль, также узнали, что такое комплексные числа и как их возводить в степень. Всё оказалось куда проще, чем вы думали. Не так ли? Остаётся лишь попробовать всё на своём опыте, и всё встанет на свои места. Любая задача, связанная с возведением в степень, теперь решается очень легко для вас.
Существует огромное число языков программирования, и Паскаль занимает среди них не последнее место. И если вы собираетесь в дальнейшем серьезно заниматься программированием, следует начинать знакомство с этим миром именно с изучения данного языка, так как он более прост в восприятии и, что немаловажно, программа абсолютно бесплатна.
В статье мы разберем такую непростую проблему, как возведение в степень. Паскаль, увы, не предоставляет нам для решения данной задачи, в отличие от других языков программирования, отдельного оператора. Так что здесь приходится, как говорится, выкручиваться подручными средствами, прибегая к циклам и математическим операторам - именно здесь мы можем дать волю нашей фантазии. Рассмотрим несколько методов решения данной проблемы.
Пусть нам дана самая простая задача, где некое число необходимо возвести в целую положительную степень. Допустим, число a возводим в 4 степень. Здесь выполняется простая математическая операция: b:=a*a*a*a.

В следующем шаге мы усложним задачу и составим универсальную программу, которая будет возводить любое число в любую целую положительную степень. Здесь есть возможность воспользоваться любым циклом, но мы рассмотрим более простой метод с использованием цикла со счетчиком. На изображении слева вы можете ознакомиться с полным текстом нашей программы, там же есть и пояснения выполняемых операций. Кстати, следует отметить, что возводимое число a необязательно задавать Integer, а можно, допустим, Real, что позволит возвести в степень дробное число.
Предыдущие примеры позволяют нам возводить числа только в целые положительнные степени. Но встречаются задачи, где необходимо возвести число в дробную степень. При написании такой программы нам необходимо знание свойств логарифмов. В частности: a b =e b ln a . Исходя из этого, нужный фрагмент нашей программы будет иметь вид: r:=exp(b*ln(a)). Но здесь мы сталкиваемся с тем, что этот оператор не работает с нулем и отрицательными числами. Для того, чтобы наша программа выполняла возведение в степень 0, нужно задать условие: If b=0 Then r:=1 Else r:=exp(b*ln(a)). Но как же для отрицательного числа выглядит возведение в степень?

Паскаль снова заставляет нас задуматься. Здесь приходится производить данную операцию с модулем нашего числа и брать данные с отрицательным результатом. Затем проверить четность степени: если наша степень была четной, тогда мы берем от результата модуль. В таком случае наша программа будет иметь вид: r:=(-1)*exp(b*ln(abs(a))); If Round(b/2)=b/2 Then r:=abs(r). Условие здесь проверяет, четная или нет степень.
В итоге мы подходим к более универсальной модели нашей программы, которая будет работать с любыми числами. То есть теперь мы должны объеденить в единое целое все вышеизложенное. В изображении справа вы можете ознакомиться с полным текстом нашей готовой программы. Обратите внимание на заданный тип данных. В отличие от первой программы, здесь используется Real, т.к. здесь мы уже работаем с любыми числами, а не только с целыми. Итак, возведение в степень действительных чисел нами полностью рассмотрено. Осталось рассмотреть лишь один вопрос.

Переходя к нему, следует отметить, что при решении данной задачи необходимы достаточно глубокие знания в программировании. Это возведение в степень комплексного числа. Здесь можно пробовать использовать различные варианты решения, допустим, формулу Муавра, но там есть трудности с переводом комплексного числа в тригонометрическую форму. Есть решение данной задачи в задании процедуры перемножения двух комплексных чисел и простого цикла со счетчиком, т.е. повторение этой процедуры равное степени число раз. На предоставленном примере вы можете более детально разобраться с текстом этой программы.
Читайте также:


