Как сделать механизм домино
Вы, наверняка, видели гигантские шахматы, которыми можно играть в парке или на даче. Так вы можете сочетать умственную и физическую активность. Но сделать такие шахматы своими руками очень сложно, а вот изготовить огромное домино можно без проблем. Именно это мы и предлагаем сделать.
Материалы и инструменты для изготовления домино:
- довольно широкие доски (зависит от того, насколько большое домино вы хотите изготовить)
- темная морилка
- белая краска
- малярная кисть
- циркулярная пила
- шлифмашина
Как сделать домино
Приготовьте необходимое количество досок. Длина каждой кости домино должна быть вдвое большее ширины доски. Таких костей должно быть 28 штук.
Распилите дощечки на одинаковые прямоугольники. С помощью шлифмашины ошкурьте все грани.
Обработайте дощечки морилкой. Если они получились недостаточно темными, морилку можно нанести повторно. Дайте морилке просохнуть.
Проведя полоску белой краской, разделите каждую кость на две половины.
Нанесите метки на кости:
- два нуля, а затем от 0/1 до 0/6
- две единицы, а затем от 1/2 до 1/6
- две двойки, а затем от 2/3 до 2/6
- две тройки, а затем от 3/4 до 3/6
- две четверки, а затем 4/5 и 4/6
- две пятерки и 5/6
- две шестерки.
Дайте краске высохнуть. Гигантские кости домино готовы.
Понравилась статья? Подпишитесь на канал, чтобы быть в курсе самых интересных материалов
Одна из первых действительно интересных задач по математике, с которыми я столкнулся формулируется так: "из шахматной доски вырезали две противоположные по диагонали угловые клетки, можно ли оставшуюся часть разрезать на "доминошки" — фигурки из двух клеток, у которых одна сторона общая?". У нее очень простая формулировка, в отличие от великой теоремы Ферма она имет простое, элегантное, но неочевидное решение (если вы знаете решение задачи, то попробуйте применить его к фигуре справа).


В этой статья я расскажу о нескольких алгоритмах, которые умеют покрывать доминошками произвольную клетчатую фигуру на плоскости, если это возможно, находить ситуации, когда это невозможно и считать количество возможных замощений доминошками.
Nota bene! Материал этой статьи — это усеченный вариант вот этого jupyter-notebook, все картинки и анимации, которые вы увидите в статье, сгенерированы кодом из этого ноутбука (правда анимаций не будет в github предпросмотре). К слову, картинки из заголовка также сгенерированы с помощью python/matplotlib
Сделать это невозможно, и этому есть красивое и простое объяснение:
- На оставшейся части доски 30 черных и 32 белых клетки
- Каждая доминошка состоит из одной черной и одной белой клетки
- Как бы мы не разрезали фигуру на доминошки, в итоге на доминошках будет равное число белых и черных клеток
Динамическое программирование по профилю
Про динамического программирования есть статья на хабре, которая даже содержит пример с покрытием доминошками, я немного расширю этот пример.
Основная суть динамического программирования заключается в том, чтобы придумать для исходной задачи какие-то промежуточные подзадачи так, чтобы их можно было легко друг через друга выразить. Например, если мы хотим вычислить двухсотое число Фибоначчи, то для этого можно последовательно вычислить все числа Фибоначчи вплоть до нужного нам применяя соотношение
Аналогично можно вычислить число "сочетаний" , воспользовавшись одним из следующих рекуррентных соотношений
Для задачи "можно ли замостить доминошками прямоугольник ?" к сожалению подобных простых соотношений не существует. Тем не менее, если мы рассмотрим более широкий класс фигурок, то такие соотношения уже станут возможными, главное чтобы это не были слишком маленькие классы и динамическое программирование не превратилось в банальный перебор.
Посмотрим на следующий класс фигурок: у нас есть прямоугольник , на строке присутствуют первые клеток, остальные задаются профилем, на строке первые клеток задаются профилем, остальные не участвуют. Профиль — это последовательность нулей и единичек длины : если на -ой позиции профиля единичка, это значит что в этой фигуре есть соответствующая клетка, всего профилей (красные клетки — единички, синие — нули).

Профиль однозначно задается числом (его бинарное представление вплоть до разрядов является последовательностей нулей и единичек).
Прямоугольник соответствует фигуре с , и нулевым профилем. На фигурках такого типа мы можем считать две основные функции
- Максимальное возможное число покрытых доминошками клеток в этой фигуре
- Количество способов полностью покрыть доминошками эту фигуру
Давайте обозначим за количество способов замостить такую фигурку, тогда и при этом выражается через сумму нескольких , по большому счету переход от к — это перебор трех случаев: поставить вертикальную доминошку, если это возможно
горизонтальную доминошку, если это возможно
и пропустить занятую клетку. В случае, если мы пытаемся понять, какое максимальное число клеток фигурки возможно замостить, то сумма заменяется на максимум и добавляется один несложный переход — пропуск свободной клетки. Важным моментом также является то, что мы можем заранее вырезать несколько клеток, принципиально от этого ничего не поменяется.
Давайте теперь попробуем реализовать это (кода будет много, так что большинство я вынесу в спойлер). Зададим интересующий нас прямоугольник как множество строк из точек и решеток (точка — свободная клетка, решетка — занятая), пока все клетки будут свободными, потом потихоньку будем какие-нибудь вырезать
Сверяемся с википедией, пока все в порядке. Давайте еще на всякий случай проверим, количество способов замостить полоску — должно получиться число Фибоначчи.
Что ж, поехали дальше, проверим на доске с вырезанными углами
Супер. Допустим вычислять количество мы научились, может найдем хотя бы одно конкретное замощение для наглядности?

Слишком просто, давайте вырежем несколько клеток

Попробуем теперь сделать тоже самое для замощения максимальной возможной части фигуры
И попробуем фигурку из заголовка

Опа! Не получилось, в общем так и должно было быть. Прежде, чем пойти дальше пару слов о сложности алгоритмов. Всего фигурок , все переходы константные, отсюда асимптотика , которая может быть улучшена до если добавить транспонирование в случае, если . Построение конкретного замощения в приведенных реализациях имеет сложность , но можно сделать так, чтобы было просто , но это банально больше кода.
Замощение с помощью решения задачи о максимальном паросочетании
Возвращаясь к черно-белой раскраске как на шахматной доске можно заметить интересную интерпретацию задачи замощения доминошками. Давайте посмотрим на граф, в котором клетки фигуры — это вершины, ребрами соединены клетки, имеющие общую сторону. Так вот, доминошка в этом графе — это как раз ребро. Если раскрасить граф в шахматном порядке, то внезапно можно обнаружить, что этот граф — двудольный, черные — одна доля, белые — другая. Если переформулировать задачу замощения наибольшего числа клеток в терминах этого графа, то получается, что нужно найти максимальное по размеру множество ребер такое, чтобы вершины являлись концом не более одного ребра. В общем то, это довольно известная задача о максимальном паросочетании. Давайте попробуем её применить для решения этой задачи, тут получится даже с анимацией, приведу базовый алгоритм Куна для нахождения максимального паросочетания.
Здесь даже получается проанимировать процесс
Суть алгоритма Куна (да и любого другого алгоритм для нахождения максимального паросочетания) заключается в нахождении "аугментирующих путей". В терминах доминошек это цепочка из доминошек, у которой рядом с доминошками на концах есть по свободной клетке, такие цепочки можно заменить на цепочки большей длины, охватывающие те же клетки и заполняя две свободные клетки рядом с концами цепочки. Более того, основное утверждение, на котором работают все алгоритмы нахождения максимального паросочетания, заключается в том, что если такой цепочки не удается найти, то значит большего замощения нам не получить.
UPD. Для последнего примера простое обоснование на основе черно-белой раскраски не работает. Насколько мне известно, есть два общих критерия для существования полного замощения:
Проверка условий этой теоремы вычислительно сложнее, чем построить максимальное паросочетание. про это я мало что знаю
Недавно меня навели на очень интересную статью про замощения, там в том числе описывается про использовании групп для доказательства невозможности различных замощений.
Бонус! Раскраска планарного графа в 5 цветов.
Для визуализации замощения я использовал отдельный цвет для каждой доминошки. К сожалению некоторые цвета не очень хорошо смотрятся, а некоторые плохо контрастируют друг с другом. В этом случае подобрать цвета для хорошего контраста не так уж просто, особенно если доминошек много. Зато можно использовать меньше цветов: доминошки, которые не находятся рядом друг с другом можно раскрасить в одинаковый цвет, тогда визуально все еще будет понятно, как именно выглядит покрытие. В общем то это классическая задача о раскраске вершин планарного графа. Любой планарный граф можно покрасить в 4 цвета, правда хорошего алгоритма для такой покраски нет. Зато есть довольно простой алгоритм для покраски в 5 цветов, когда правда все еще много, и я его мало тестировал (если необходим 5ый цвет, то возможны баги)
Если вы собираетесь использовать этот код, то обратите внимание, что там происходит отрисовка каждого шага — это было нужно для анимации, что сильно замедляет алгоритм. Если вам нужна только конечная покраска, то уберите весь код, задействующий переменную slices.
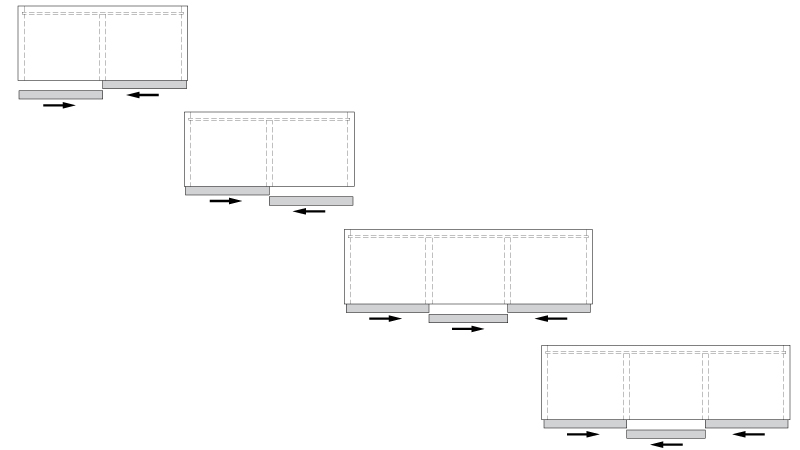
Domino – это система, предназначенная для изготовления отдельно стоящих шкафов-купе с раздвижными фасадами. Система рассчитана на изготовление шкафов шириной до 3-х метров.
Domino – это система, предназначенная для изготовления отдельно стоящих шкафов-купе с раздвижными фасадами. Система рассчитана на изготовление шкафов шириной до 3-х метров. Это единственная система развдижения с возможностью открывания центральной внешней двери в обоих направлениях. При этом шкаф может быть как трехдверным, так и двухдверным.
- Простота. Мы создали комплекты фурнитуры для двухдверного и для трехдверного решения, поэтому вам потребуется всего 2 минуты, чтобы определиться с набором фурнитуры для Вашего шкафа.
- Удобство монтажа. Для ускорения установки мы предлагаем адаптер быстрого крепления нижней скобки.
- Низкая цена при наивысшем качестве.
- Итальянский стиль и качество
Как правильно подобрать комплект?
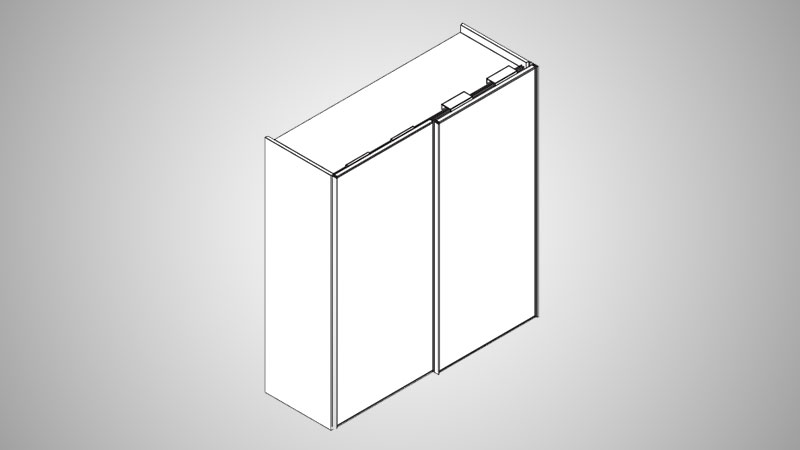
Для двухдверного шкафа
DOMINO – ДВУХДВЕРНЫЙ ВАРИАНТ:
- Выбираем направляющие
- Выбираем комплект фурнитуры, в зависимости от толщины фасада 16-21 мм или 22-28 мм
- Выбираем адаптер для крепления скобок нижних кареток (если необходимо)
- Выбираем комплект доводчиков для 2-х дверей в зависимости от веса фасада до 40 или до 60 кг (если необходимо)
DOMINO S – ДВУХДВЕРНЫЙ ВАРИАНТ:
- Выбираем направляющие
- Выбираем комплект фурнитуры, в зависимости от толщины фасада 16-21 мм или 22-28 мм
- Выбираем комплект доводчиков для 2-х дверей в зависимости от веса фасада до 40 или до 60 кг (если необходимо)

Для трехдверного шкафа
DOMINO – ТРЕХДВЕРНЫЙ ВАРИАНТ:
- Выбираем направляющие
- Выбираем комплект фурнитуры, в зависимости от толщины фасада 16-21 мм или 22-28 мм
- Выбираем адаптер для крепления скобок нижних кареток (если необходимо)
- Выбираем комплект доводчиков для 2-х дверей в зависимости от веса фасада до 40 или до 60 кг (если необходимо)
- Выбираем комплект доводчиков для центральной двери (если необходимо).
DOMINO S – ТРЕХДВЕРНЫЙ ВАРИАНТ:
- Выбираем направляющие
- Выбираем комплект фурнитуры, в зависимости от толщины фасада 16-21 мм или 22-28 мм
- Выбираем комплект доводчиков для 2-х дверей в зависимости от веса фасада до 40 или до 60 кг (если необходимо)
- Выбираем комплект доводчиков для центральной двери (если необходимо).
Таблица по подбору элементов системы в зависимости от конструкции шкафа
Шаг 1.
Выбираем артикул комплекта фурнитуры.
Шаг 2.
Выписываем верхнюю и нижнюю направляющие
Шаг 3.
Выбираем дополнительные опции
Для ускорения монтажа мы предлагаем адаптер быстрого крепления нижней скобки.
Вы, наверняка, видели гигантские шахматы, которыми можно играть в парке или на даче. Так вы можете сочетать умственную и физическую активность. Но сделать такие шахматы своими руками очень сложно, а вот изготовить огромное домино можно без проблем. Именно это мы и предлагаем сделать.

Материалы и инструменты для изготовления домино:
- довольно широкие доски (зависит от того, насколько большое домино вы хотите изготовить)
- темная морилка
- белая краска
- малярная кисть
- циркулярная пила
- шлифмашина
Как сделать домино
Приготовьте необходимое количество досок. Длина каждой кости домино должна быть вдвое большее ширины доски. Таких костей должно быть 28 штук.
Распилите дощечки на одинаковые прямоугольники. С помощью шлифмашины ошкурьте все грани.

Обработайте дощечки морилкой. Если они получились недостаточно темными, морилку можно нанести повторно. Дайте морилке просохнуть.

Проведя полоску белой краской, разделите каждую кость на две половины.

Нанесите метки на кости:
- два нуля, а затем от 0/1 до 0/6
- две единицы, а затем от 1/2 до 1/6
- две двойки, а затем от 2/3 до 2/6
- две тройки, а затем от 3/4 до 3/6
- две четверки, а затем 4/5 и 4/6
- две пятерки и 5/6
- две шестерки.

Дайте краске высохнуть. Гигантские кости домино готовы. Можно выйти во двор и поиграть с друзьями.
Читайте также:


