Как сделать матрицу в маткаде
ü осуществить действия над матрицами в среде MathCAD.
Обеспечение работы:
ü ПК с установленными необходимыми программами для работы (MathCad);
ü методические указания к выполнению работы (электронный вариант).
Порядок выполнения работы:
1. Ознакомиться с теоретическим материалом данных методических указаний;
2. Выполнить задания, приведенные в разделе II. Порядок выполнения работы;
3. Ответить на контрольные вопросы, сделать выводы.
4. Оформить отчет.
Содержание отчета:
ü тема, цель и порядок выполнения работы;
ü привести выполненные задания (скриншоты);
ü ответы на контрольные вопросы;
Теоретические положения
I. СОЗДАНИЕ ВЕКТОРОВ И МАТРИЦ В MATHCAD
В пакете MathCAD кроме матриц имеется особый класс переменных, который часто используется для замены так называемых управляющих структур (циклов). Этот класс носит название дискретные переменные. Эти переменные задаются двумя способами.
Способ 1. Используется для задания фиксированных целочисленных значений. Шаблон имеет вид:
Name := Nbegin .. Nend,
åv –получить сумму элементов,
x y × –скалярное произведение векторов,
x´y –векторное произведение векторов.
Система MathCAD также представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).
На рис. 2.4 представлены вычисления с использованием операций над матрицами.

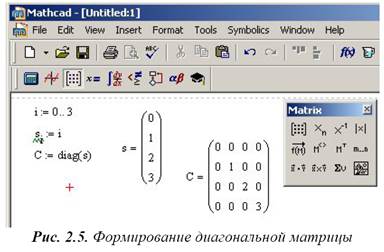
Пример 2.3.Требуется сформировать диагональную квадратную матрицу с(6x6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.
Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начинается с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 2.5.
Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 2.6.

Пример 2.5.Даны две матрицы A с размерностью 2.3 и В с размерностью 3.3. Требуется объединить эти матрицы в одну матрицу С(5.3), так чтобы в новой матрице в качестве первых строк располагались строки матрицы А, а за ними должны следовать строки матрицы В.

Пример 2.6.Дана матрица A с размерностью 5.5. Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2 по номер 4, и столбцах, начиная с номера 0 по номер 5.
Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет пять параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 2.8.

Пример 2.7.Дана матрица A(3.3). Требуется получить из заданной матрицы A два вектора. Первый вектор B должен совпадать с четвёртым столбцом матрицы А, второй вектор С – с третьей строкой матрицы А.

Пример 2.8.Из матрицы А(6.6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.
Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 2.10.
Использование матриц специального вида для выполнения матричных операций в системе MathCAD. Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i-й элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i-й строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементу i-ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
Пример 2.9.Дана матрица A(4x4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с нулевым столбцом матрицы А, а второй – с 3-м столбцом матрицы А.
Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1– с единичным значением в строке с номером 0, а второй вектор В2 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 2.11.

Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор-строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 2.10.Дана матрица A(4.4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц (рис. 2.12).

Пример 2.11.Дана матрица (4.4). Требуется найти сумму элементов в третьем столбце матрицы.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение (рис. 2.13).

Пример 2.12.Дана матрица: A(4.4). Требуется получить вектор, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение (рис. 2.14).

Указываем размерность матрицы, rows – количество строк, columns – количество столбцов. Жмем Ок.
Последний элемент матрицы равен (нумерация первого элемента начинается с нуля)
Найдем максимальное значение матрицы max(X)
Найдем минимальное значение матрицы min(X)
Среднее значение матрицы равно
Первая матрица-столбец равна
Транспонирование матрицы в Mathcad X T
Вычисление обратной матрицы

Вычисление определителя матрицы
Умножение матрицы на матрицу

Сложение матриц — сумма элементов матрицы Mathcad

Возведение матрицы в степень

Далее, создадим две матрицы в виде векторов 3×1 и 1×3
Здесь A – матрица-столбец; B – матрица-строка
Первый элемент вектора A (нумерация начинается с нуля) равен
Количество элементов в матрице-столбце через функцию length(A) равно
Найдем значения для функции ln x, подставив значения матрицы A
Сортировка вектора sort(А)
Количество элементов в векторе rows(A), cols(A)
Векторное произведение в Mathcad



Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 0 / 5. Количество оценок: 0
Оценок пока нет. Поставьте оценку первым.

1021
Вы здесь: Всё о Mathcad Всё о Mathcad Матричные вычисления
Решение системы линейных алгебраических уравнений матричным способом в Mathcad

Решение системы линейных алгебраических уравнений методом Крамера в Mathcad
В Mathcad метод Крамера также предназначен для решения системы n линейных уравнений с n неизвестными вида A*x =b на основе предварительного вычисления определителей системы, при условии, что определитель матрицы А отличен от нуля. Метод основан на формулах Крамера, вида , где – определитель матрицы, полученной из матрицы А системы заменой i –го столбца, т.е. столбца коэффициентов при неизвестном Xi вектором свободных членов, т.е. b. На листинге в Mathcad приведен пример решения системы линейных алгебраических уравнений методом Крамера.
Матрицы и векторы в Mathcad
Операции, выполняемые над векторами и матрицами в Mathcad, можно разбить на две большие группы. К первой группе относятся операции, которые применяются к отдельным векторам и матрицами. Например, транспонирование матрицы или вычисление обратной матрицы в Mathcad. Ко второй группе относятся операции, которые выполняются над группой векторов и матриц. Как правило, они выполняются над двумя матрицами или матрицей и вектором. Например, сложение, вычитание матриц, перемножение матриц или умножение матрицы и вектора. К векторам и матрицам в Mathcad, при выполнении операций над ними, могут предъявляться определенные требования в соответствии с требованиями классической математики. Например, при перемножении матрицы и вектора, количество столбцов матрицы должно быть равно количеству срок вектора. Поэтому при работе с векторами и матрицами пользователь должен иметь необходимую математическую подготовку. В таблице приведены основные операции, выполняемые над векторами и матрицами, используемые в Mathcad. В таблице приняты следующие обозначение: А – массив, под которым понимается вектор или матрица, М – матрица, z - скаляр, v – вектор.
Наиболее удобно выполнять матричные вычисления с использованием кнопок панели инструментов “Матрица”. По умолчанию индексация строк и столбцов элементов матрицы начинается с 0. Для того чтобы индексация начиналась с 1, необходимо системной переменной ORIGIN присвоить значение 1. На листинге приведен пример матричных вычислений в Mathсad.
Матричные функции в Mathcad
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Среди функций, предназначенных для создания матриц, следует выделить функцию matrix(L,N,f), где L – число строк матрицы, N – число столбцов матрицы, f – функция f(l,n) при . Другая функция из этой группы identity(n). Функция предназначена для создания единичной матрицы размерности n. Следующая функция geninv(M) позволяет осуществить обращение матрицы M, аналогично операции M -1 .
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
Матричные вычисления в Mathcad
Создание векторов и матриц реализовано в Mathсad различными способами. В данном разделе рассматриваются только функции и операции с векторами и матрицами, а так же прикладное использование векторов и матриц для решения некоторых задач.
Матричные функции
В Mathсad очень много функций, предназначенных для работы с матрицами и векторами.
Основные операции с матрицами и векторами
Операции, выполняемые над векторами и матрицами, можно разбить на разные большие группы.
Решение системы линейных алгебраических уравнений матричным способом
В Mathcad можно решать системы линейных алгебраических уравнений матричным способом.
Решение системы линейных алгебраических уравнений методом Крамера
Также предназначен метод Крамера для решения системы n линейных уравнений с n неизвестными.

Создать матрицу из 0 и 1
Необходимо создать матрицу (или вектор) определенной размерности, состоящую из 0 и 1, НО(!).

Создать матрицу по правилу
Матрица 10 на 10 _=\left\i+j, i\neq j\\ 1, i=j\end\right.
Как создать динамическую матрицу ?
Есть три таблицы хочу создать из них матрицу или три вектора но в матричной записи .

Создать матрицу значений заданного распределения
Нашел пример для нахождения значений координат для заданного распределения, но результипующая.
Читайте также:






