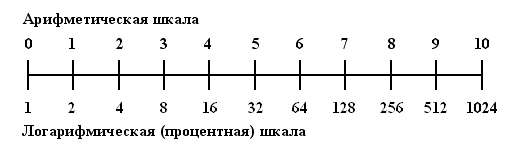
Как сделать логарифмическую шкалу
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Word 2016 Outlook 2016 PowerPoint 2016 Excel 2016 для Mac Word 2016 для Mac PowerPoint 2016 для Mac Excel 2013 Word 2013 Outlook 2013 PowerPoint 2013 Excel 2010 Word 2010 Outlook 2010 PowerPoint 2010 Excel 2007 Word 2007 Outlook 2007 PowerPoint 2007 Excel для Mac 2011 Word для Mac 2011 PowerPoint для Mac 2011 Excel Starter 2010 Больше. Основные параметры
По умолчанию Microsoft Office Excel задает при создании диаграммы минимальное и максимальное значения шкалы вертикальной оси (оси значений, или оси Y). Однако шкалу можно настроить в соответствии со своими потребностями. Если отображаемые на диаграмме значения охватывают очень широкий диапазон, вы также можете использовать для оси значений логарифмическую шкалу.
На диаграмме щелкните ось значений, которую вы хотите изменить, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
Щелкните в любом месте диаграммы.
Откроется вкладка Работа с диаграммами с дополнительными вкладками Конструктор и Формат.
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Элементы диаграммы, а затем щелкните Вертикальная ось (значений).

На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного.
В диалоговом окне Формат оси в разделе Параметры оси выполните одно или несколько из следующих действий:
Важно Эти параметры доступны только в том случае, если выбрана ось значений.
Чтобы изменить число, с которого начинается или заканчивается вертикальная ось (значений), в поле "Минимальное значение" или "Максимальное значение" введите другое число. При необходимости вы можете нажать кнопку "Сброс", чтобы вернуть исходное значение.
Чтобы изменить интервал делений и линий сетки диаграммы, для параметра "Основные единицы" или "Основные единицы" введите другое число в поле "Основные единицы" или "Мелкие единицы". При необходимости вы можете нажать кнопку "Сброс", чтобы вернуть исходное значение.
Чтобы изменить порядок значений, установите флажок Обратный порядок значений.
Примечание При изменении порядка значений на вертикальной оси (значений) подписи категорий по горизонтальной оси (категорий) зеркально отобразятся по вертикали. При изменении порядка категорий слева направо подписи значений зеркально отобразятся слева направо.
Чтобы применить к оси значений логарифмическую шкалу, установите флажок Логарифмическая шкала.
Примечание Логарифмическую шкалу нельзя использовать для представления отрицательных значений и нуля.
Чтобы изменить единицы, отображаемые для оси значений, выберите нужный вариант в списке Отображаемые единицы.
Для вывода подписи, описывающей единицы измерения, установите флажок Отображать на диаграмме.
Совет. Измените единицы, если значения являются большими числами, которые вы хотите сделать более краткими и понятными. Например, можно представить значения в диапазоне от 1 000 000 до 50 000 000 как значения от 1 до 50 и добавить подпись о том, что единицами являются миллионы.
Чтобы изменить положение делений и подписей оси, в разделе "Деления" выберите нужные параметры в полях Главные и Дополнительные.
Щелкните стрелку раскрывающегося списка в разделе Подписи и выберите положение подписи.
Для изменения точки, в которой горизонтальная ось (категорий) пересекает вертикальную (значений), в разделе Основание пересекает установите переключатель Значение оси и введите число в текстовое поле. Также можно установить переключатель Максимальное значение по оси, чтобы указать, что горизонтальная ось (категорий) пересекает вертикальную ось (значений) в самом большом значении.
Примечание При выборе параметра Максимальное значение по оси подписи категорий перемещаются на другую сторону диаграммы.

На диаграмме щелкните ось значений, которую вы хотите изменить, или выберите ее в списке элементов диаграммы с помощью указанных ниже действий.
Щелкните в любом месте диаграммы.
Откроется панель Работа с диаграммами с дополнительными вкладками Конструктор, Макет и Формат.
На вкладке Формат в группе Текущий фрагмент щелкните стрелку рядом с полем Элементы диаграммы, а затем щелкните Вертикальная ось (значений).
На вкладке Формат в группе Текущий фрагмент нажмите кнопку Формат выделенного фрагмента.
В диалоговом окне Формат оси в разделе Параметры оси выполните одно или несколько из следующих действий:
Важно Эти параметры доступны только в том случае, если выбрана ось значений.
Чтобы изменить число, с которого начинается или заканчивается вертикальная ось (значений), выберите параметр "Минимальное или максимальное значение" и введите другое число в поле "Минимальное значение" или "Максимальное значение".
Чтобы изменить интервал делений и линий сетки диаграммы, для параметра "Основные единицы" или "Основные единицы" нажмите кнопку "Фиксированная" и введите другое число в поле "Основные единицы" или "Основные единицы".
Чтобы изменить порядок значений, установите флажок Обратный порядок значений.
Примечание При изменении порядка значений на вертикальной оси (значений) подписи категорий по горизонтальной оси (категорий) зеркально отобразятся по вертикали. При изменении порядка категорий слева направо подписи значений зеркально отобразятся слева направо.
Чтобы применить к оси значений логарифмическую шкалу, установите флажок Логарифмическая шкала.
Примечание Логарифмическую шкалу нельзя использовать для представления отрицательных значений и нуля.
Чтобы изменить единицы, отображаемые для оси значений, выберите нужный вариант в списке Отображаемые единицы.
Для вывода подписи, описывающей единицы измерения, установите флажок Отображать на диаграмме.
Совет. Измените единицы, если значения являются большими числами, которые вы хотите сделать более краткими и понятными. Например, можно представить значения в диапазоне от 1 000 000 до 50 000 000 как значения от 1 до 50 и добавить подпись о том, что единицами являются миллионы.
Чтобы изменить положение делений и подписей оси, выберите нужные параметры в полях Основные, Промежуточные и Подписи осей.
Для изменения точки, в которой горизонтальная ось (категорий) пересекает вертикальную (значений), в разделе Горизонтальная ось пересекает щелкните Значение оси и введите число в текстовое поле. Также можно щелкнуть Максимальное значение по оси, чтобы указать, что горизонтальная ось (категорий) пересекает вертикальную ось (значений) в самом большом значении.
Примечание При выборе параметра Максимальное значение по оси подписи категорий перемещаются на другую сторону диаграммы.
Выбор типа шкал для графика, всегда казалось мне интуитивно понятной задачей. Однако, когда мне нужно было объяснить, чем они отличаются, то я не смог привести понятных аргументов. В интернете хорошей информации мне не попалось. Поэтому решил разобраться, откуда растут ноги у разных видов шкал и как их следует применять. Я решил рассмотреть три самых распространенных вида шкал — равномерную, логарифмическую и степенную.
Равномерная шкала

Самый распространенный и привычный вид шкал. Также их называют арифметическими или линейными шкалами. На такой шкале значения равноудалены друг друг от друга.
Например значения 100 и 200, и 200 и 300 отстают друг от друга на одно и тоже расстояние.
Например, на этом графике по оси Y — равномерная шкала с шагом в 20 лет средней продолжительности жизни, а по оси X — равномерная шкала с шагом 10 календарных лет.

Логарифмическая шкала

Этот вид шкал тоже используется достаточно часто, особенно когда речь идёт о научных исследованиях. Она используется для отображения широко диапазона величин, когда значения, которые попадают на график отличаются на много порядков. То есть когда мы хотим одновременно видеть и значения 0.1, 0.2 и значения 100, 200 на одном графике. Зачастую это связанно с физикой процесса. Так, например, в музыке ноты, различающиеся по частоте в два раза это ноты на октаву выше (Ля и Ля следующей октавы). Чтобы показать частоты двух нот будет удобно использовать логарифмическую шкалу.
Но бывает, что в наборе данных просто содержаться большой разброс данных. Например, как на этом графике из Beautiful Evidence Тафти, где он использует логарифмические шкалы для сравнения массы тела и мозга различных существ. Так как бывают и крошечные рыбки и огромные киты, то на таком графике удобно использовать логарифмические шкалы.

Чаще всего используются логарифмические шкалы с основанием 10. Это значит, что одинаковые расстояние на графике откладываются между значениями отличающимися на один порядок. Но бывают логарифмические шкалы с другими основаниями. Например 2.
Степенная шкала

Со степенной шкалой
С равномерной шкалой
То есть степенные шкалы используются когда данные смещены в ту или иную сторону.
Сравнение шкал
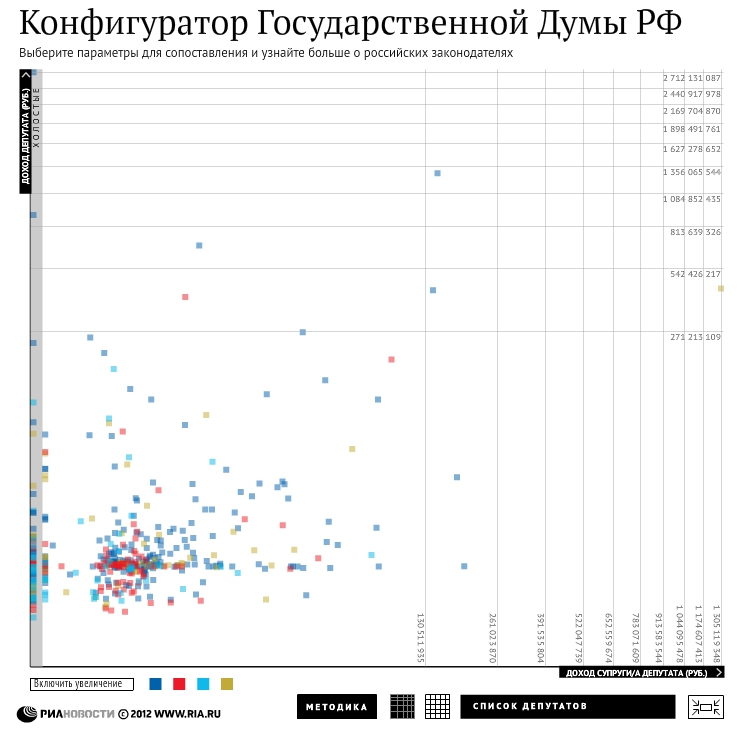
Чтобы удобно сравнить и понять как использовать ту или иную шкалу, я сделал небольшой инструмент. На нём можно выбрать разные наборы данных и понять, как они выглядят на разных шкалах.
Мы обычно думаем о количественных масштабах как о линейных, с равными количествами от одного помеченного значения до следующего. Например, количественная шкала от 0 до 1000 может быть разделена на равные интервалы по 100 каждый. Линейные масштабы кажутся нам естественными.
Оглавление
Логарифмы и их шкалы
Мы обычно думаем о количественных масштабах как о линейных, с равными количествами от одного помеченного значения до следующего. Например, количественная шкала от 0 до 1000 может быть разделена на равные интервалы по 100 каждый. Линейные масштабы кажутся нам естественными. Если бы мы проехали на машине 1000 миль, мы могли бы представить, что это расстояние разделено на десять сегментов по 100 миль. Маловероятно, что мы представили бы, что он разделен на четыре логарифмических сегмента, состоящих из 1, 9, 90 и 900-мильных интервалов. Точно так же мы думаем о проходе времени – также количественном – с точки зрения дней, недель, месяцев, лет, десятилетий, столетий или тысячелетий; интервалы, которые равны (или в случае месяцев, приблизительно равны) по продолжительности.
Логарифмы и их шкалы весьма полезны в математике, а иногда и в анализе данных, но они полезны только для представления данных в тех относительно редких случаях при обращении к аудитории, которая состоит из тех, кто был обучен мыслить логарифмами. С обучением мы можем научиться мыслить логарифмами, хотя я сомневаюсь, что это когда-нибудь будет так же легко и естественно, как мышление в линейных единицах.
В своих собственных аналитических целях я использую логарифмические шкалы, главным образом, для одной задачи: сравнивать скорости изменения. Когда два временных ряда отображаются на линейном графике, использование логарифмической шкалы позволяет нам легко сравнивать скорости изменения вдоль двух линий, сравнивая их наклоны, поскольку равные наклоны представляют равные скорости изменения. Это работает, потому что единицы измерения по логарифмической шкале увеличиваются на величину (например, в десять раз по сравнению с предыдущим значением для шкалы 10 на основе бревна или в два раза больше предыдущего значения для шкалы на основе 2 базы), а не на величину. Однако даже в этом случае я бы не стал сообщать другим о том, что я обнаружил о скоростях изменений, используя график с логарифмической шкалой, поскольку все, кроме нескольких человек, неправильно это поняли бы.

Самая темная линия, которая представляет распределение дохода на душу населения в мире в 2015 году, отмечена звездочкой на этом графике. Он имеет вид нормального колоколообразного распределения. Эта форма предполагает справедливое распределение доходов, но более внимательно. В частности, обратите внимание на шкалу доходов вдоль оси X. Хотя метки вдоль шкалы не всегда представляют логарифмические приращения – странные, но никогда не объясняемые – шкала действительно логарифмическая. Если бы использовалась линейная шкала, распределение дохода было бы значительно искажено с пиком ближе к нижнему концу и длинным хвостом, простирающимся вправо. Я не могу придумать никакой веской причины для использования логарифмической шкалы в этом случае. Линейная шкала в диапазоне от 0 долл. США в день на нижнем уровне до 250 долл. США в день или около того на верхнем уровне будет работать нормально. Обычно интервалы в 25 долларов будут работать хорошо для диапазона 250 долларов, разбивая шкалу на десять интервалов, но это не позволит определить порог крайней бедности, составляющий чуть менее 2,00 долларов, поскольку он будет скрыт в начальном интервале от 0 до 25 долларов. , Чтобы удовлетворить эту конкретную потребность, можно использовать крошечные интервалы по 2 долл. США каждый по всей шкале, что создает крайнюю нищету примерно в пределах первого интервала. В качестве альтернативы можно использовать более крупные интервалы, и процент людей, находящихся ниже порога крайней бедности, можно обозначить цифрой.
После тщательного изучения графика Пинкера у вас может возникнуть соблазн утверждать, что его логарифмическая шкала дает преимущество, заключающееся в более четкой картине распределения дохода в крошечном диапазоне от 0 до 2,00 долларов. Это, однако, не является его целью. Даже если этот уровень детализации относился к делу, информация, которая появляется в этом диапазоне, не является реальной. Исходные данные, на которых основан этот график, не достаточно точны, чтобы представить, как доход распределяется между $ 0 и $ 2,00. Если бы существовали надежные данные, и нам действительно нужно было четко показать, как распределяется доход от 0 до 2 долларов, мы бы создали отдельный график, чтобы показать только этот диапазон, и этот график будет использовать линейную шкалу.
Когда я заметил, что Пинкер получил график из Gapminder и приписал его Оле Рослингу, я решил посмотреть, ввел ли Пинкер логарифмическую шкалу или унаследовал ее в этой форме от Gapminder. Проверив, я обнаружил, что графики распределения богатства Gapminder’а действительно имеют логарифмическую шкалу. Если вы перейдете на ту часть веб-сайта Gapminder, которая позволяет вам использовать их инструменты визуализации данных, вы обнаружите, что вы можете только логарифмически просматривать распределение богатства. Хотя некоторые из графиков Gapminder предоставляют возможность переключения между линейным и логарифмическим масштабами, те, которые отображают распределение богатства, этого не делают. Вот график, связанный с состоянием по умолчанию, который можно просмотреть с помощью инструмента Gapminder:

Это обеспечивает удобное чувство справедливости в форме колокола, что не соответствует действительности.
Чтобы представлять данные четко и правдиво, мы должны понимать, что работает для человеческого мозга, и соответственно проектировать наши дисплеи. Люди не думают логарифмами. По этой причине обычно лучше избегать логарифмических масштабов, особенно при представлении данных широкой публике. Конечно, Пинкер и Рослинг знают это.
Позвольте мне отступить от логарифмов, чтобы выявить еще одну проблему с этими графиками. Не существует практического объяснения для гладких кривых, которые они показывают, если они основаны на фактических данных о доходах. Единственный раз, когда мы видим такие плавные кривые распределения, это когда они являются результатом математических вычислений, а не когда они основаны на реальных данных. Глядя на график выше, вы можете предположить, что когда данные о распределении по каждой стране были агрегированы для представления мира в целом, агрегация каким-то образом сглаживала данные. Возможно, это возможно, но это не то, что здесь произошло. Если вы внимательно посмотрите на график выше, в дополнение к кривым в верхней части каждого из четырех цветных участков, по одному для каждого региона мира, в каждом цветном разделе есть много светлых линий. Каждая из этих светлых линий представляет данные распределения конкретной страны. Имея это в виду, посмотрите на любую из этих светлых линий. Каждая отдельная строка гладкая за пределами практической возможности быть основанной на фактических данных о доходах. Некоторая неровность вдоль линий всегда будет существовать. Это говорит нам о том, что эти графики не отображают неизменных данных о доходах ни для одной из стран. То, что мы видим, каким-то образом манипулируется. Наличие таких манипуляций всегда вызывает у меня настороженность. Данные могут сильно отличаться от фактического распределения богатства в большинстве стран.
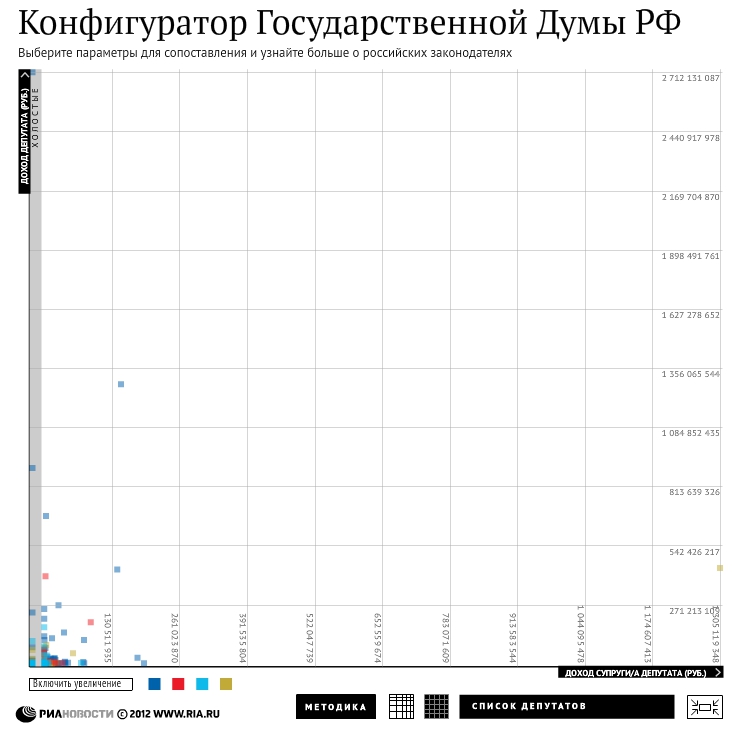
Моя настороженность усиливается, когда я изучаю данные о богатстве этого типа из давних времен. Вот график распределения доходов Gapminder за 1800 год:

Данные о доходах имеют большую неопределенность!
Есть много разных способов оценить и сравнить доход. Различные методы используются в разных странах и годах. К сожалению, не существует источника данных, который позволял бы проводить сравнения по всем странам, даже за один год. Gapminder удалось скорректировать картину для некоторых различий в данных, но по-прежнему есть большие проблемы при сравнении отдельных стран. Точную форму страны следует принимать с большим количеством соли.

Логарифмическая шкала - это шкала измерения , в которой используется логарифм физической величины вместо самой величины.
На простом примере логарифмической шкалы показаны равномерно расположенные деления на вертикальной оси графика, отмеченные цифрами 1, 10, 100, 1000, . вместо 0, 1, 2, 3, .
Представление данных в логарифмической шкале может быть полезно, когда данные охватывают широкий диапазон значений - логарифм сокращает их до более управляемого диапазона. Некоторые из наших чувств работают логарифмически ( закон Вебера-Фехнера ), что делает логарифмические шкалы особенно подходящими для представления этих величин. В частности, наш слух воспринимает равные отношения частот как равные различия в высоте тона . Кроме того, исследования маленьких детей и изолированных племен показали, что логарифмические шкалы могут быть наиболее естественным способом представления чисел людьми. [ 1 ]
Определение и основа

В логарифмической шкале с основанием 10 первые степени 10 (1, 10, 100, 1000,…) расположены с равными интервалами.

Еще одна логарифмическая шкала с основанием 10, с более высоким разрешением. Обратите внимание, что интервалы 10-20 и 10-30 эквивалентны интервалам 1-2 и 1-3 соответственно.
Логарифмические шкалы определяются как функция степеней базовой величины (базы), или вы должны согласиться измерять количество в фиксированных единицах.
Чаще всего используются основания логарифмов 10 (основание десятичных логарифмов ) и число e (основание натурального или натурального логарифма ).
Если представляемая величина не является целой степенью используемого логарифмического основания, для представления указанной меры в логарифмической шкале необходимо будет добавить аддитивную константу.
Также необходимо указать основание логарифмов, если только значение шкалы не рассматривается как размерная величина, выраженная в общих логарифмических единицах (неопределенное основание).
Примеры весов
На большинстве логарифмических шкал небольшие значения (или отношения) базовой величины (базы) соответствуют отрицательным значениям логарифмической меры. Известными примерами таких шкал являются:
Некоторые логарифмические шкалы разработаны таким образом, что большие значения (или отношения) базовой величины соответствуют малым значениям логарифмической меры. Примеры таких шкал:
-
для измерения кислотности и щелочности ; Шкала звездной величиныяркости звезд ;
- Шкала Крамбейна размеров частиц в геологии . света прозрачными образцами .
Логарифмические единицы
Логарифмические единицы - это абстрактные математические единицы, которые могут использоваться для выражения величин (физических или математических), которые определены в логарифмической шкале, то есть пропорциональны значению логарифмической функции. В этой статье некоторая логарифмическая единица будет обозначаться с помощью записи [log n], где n - положительное действительное число, а [log] здесь обозначает неопределенную функцию логарифма Log ().
Есть величины, которые определяются как абсолютные логарифмические шкалы , которые соответствуют общему выражению:
и другие относительные логарифмические шкалы , относящиеся к величине, которая используется в качестве эталона и принимает общую форму: [ 2 ]
Q знак равно k ⋅ бревно а Икс 2 Икс р е ж \ over x _ >> \ quad> Пример: громкость или звуковая мощность сигнала в децибелах.
Примеры
Примерами логарифмических единиц являются общие единицы информации , такие как бит [log 2] и байт 8 [log 2] = [log 256], а также nat [log e] и ban [log 10]; единица энтропии ( Дж / К ), единицы измерения относительной силы сигнала, такие как дБ , 0,1 [log 10] и bel [log 10], Neper [log e], и другие единицы логарифмической шкалы, такие как точка по шкале Рихтера [log 10] или (в общем) единица соответствующего порядка величины, иногда называемая множителем десять или десятилетие (в этом смысле эквивалентно [log 10], а не 10 годам).
Мотивация
Мотивация концепции логарифмических единиц заключается в том, что мы можем определить величину в логарифмической шкале в терминах логарифма определенного конкретного основания, чтобы сделать (совершенно произвольный) выбор единицы измерения указанной величины, которая соответствует с выбранным конкретным (и столь же произвольным) основанием логарифма. Из-за идентичности
Логарифмы любого заданного числа по двум разным основаниям (в данном случае b и c ) отличаются только постоянным множителем log c b . Эту константу можно рассматривать как фактор для преобразования числового представления чистой (неопределенной) логарифмической величины log a из произвольной единицы измерения (единицы [log c ]) в другую (единицу [log b ] ), в виде
L В г ( а ) знак равно ( бревно б а ) [ бревно б ] знак равно ( бревно c а ) [ бревно c ] . (a) = (\ log _ \, a) [\ log \, b] = (\ log _ \, a) [\ log \, c]. >
пер W знак равно бревно е W знак равно L В г ( W ) / [ бревно е ] . \, W = \ mathrm (W) / [\ log \, e].>
Следовательно, мы можем интерпретировать постоянную Больцмана просто как выражение (в терминах более стандартных физических единиц) для абстрактной логарифмической единицы [log e], которая необходима для преобразования безразмерной чистой числовой величины ln W (в которой используется произвольный выбор базы , называемый e) в более фундаментальной чистой логарифмической величине Log ( W ), которая подразумевает, что выбор конкретного основания не является необходимым, и, следовательно, нет конкретного выбора физической единицы измерения энтропии.
Графическое представление
Логарифмическая шкала позволяет легко сравнивать значения, которые охватывают широкий диапазон, как на этой карте, показывающей число погибших в разбивке по национальностям во время землетрясения в Индийском океане 2004 года .
Логарифмическая шкала - это также графическая шкала на одной или обеих сторонах графика, где x - это число, напечатанное на расстоянии c · log (x) от точки, отмеченной цифрой 1. Логарифмическая шкала и номограммы часто используются для логарифмической линейки. используйте логарифмические шкалы. В логарифмической шкале разность, равная по порядку величины, представлена равным расстоянием. Среднее геометрическое двух чисел находится на полпути между числами.
Логарифмическая миллиметровка до появления компьютерной графики была основным научным инструментом. Бумажные представления с полулогарифмической шкалой могут отображать экспоненциальные функции, например прямые. То же самое происходит с потенциальными функциями на бумаге с двумя логарифмическими шкалами. (см. полулогарифмический и логарифмический графики в начале статьи).

Когда необходимо представить серию значений и диапазон, который они охватывают, велик, логарифмическая шкала может предоставить средства отображения данных, которые позволяют определять значения из графика. Логарифмическая шкала представлена расстояниями, пропорциональными логарифмам представленных значений. Например, на верхнем рисунке на обоих графиках представлены значения: 2, 5, 20, 60, 320, 780, 1500, 4900.
Логарифмические и полулогарифмические графики. Уравнения линий
Представление экспоненциальной функции
В первом случае на левом графике мы видим график функции в линейном масштабе ( y по сравнению с x ). В полулогарифмическом масштабе, центральный график, получается прямая линия, как и в третьем случае, правый график, на котором ln y отображается относительно x с использованием линейных масштабов ,. Y знак равно е 0 , 5 ⋅ Икс > пер Y знак равно 0 , 5 ⋅ Икс
| у = е 0,5 х (лин-лин) | y = e 0,5 · x (лин-лог) | Ln y = Ln e 0,5 · x = 0,5 · x (логарифм) |
|---|---|---|
 |  |  |
| Линейные шкалы по обеим осям | Полулогарифмический: линейная ось X; Ось Y с логарифмической шкалой | Обе логарифмические оси |
| Представленные точки имеют значения x равные -6; -5,5; -5; -4,5;… 0; …; 4.5; 5: 5.5; 6 | ||
| Представление Ln y vs x с использованием вертикальной оси с линейным масштабом (справа) эквивалентно представлению y vs x с использованием вертикальной оси с логарифмической шкалой (в центре). В обоих случаях масштаб горизонтальной оси является линейным, и поэтому центральный график представляет собой полулогарифмическое или линейно- логарифмическое представление. | ||
То есть, при построении экспоненциальной функции в полулогарифмическом масштабе (эквивалентном представлению ln y относительно x на осях с линейными масштабами) мы получаем : , что является прямой линией . Y знак равно е а Икс > пер Y знак равно а ⋅ Икс
Представление потенциальной функции
Теперь мы видим макет функции с использованием различных возможностей. На левом графике используются линейные шкалы ( y по сравнению с x ). В логарифмическом масштабе, центральный график, получается прямая линия, как и в третьем случае, правый график, на котором ln y отображается относительно ln x с использованием линейных масштабов ,. Y знак равно Икс 4 > пер Y знак равно 4 ⋅ L п Икс
| у = х 4 (лин-лин) | у = х 4 (журнал-журнал) | Ln y = 4 · Ln x (журнал-журнал) |
|---|---|---|
 |  |  |
| Линейные шкалы | Логарифмический | Линейный |
| Представленные точки имеют значения x равные 0; 0,2; 0,4; 0,6; …; 4.2; 4,4: 4,6; 4.8. | ||
| Представление ln y vs ln x на осях с линейным масштабом (справа) эквивалентно представлению y vs x в логарифмическом представлении (обе оси с логарифмической шкалой; центр). | ||
То есть при нанесении на график потенциальной функции y = x b в логарифмическом масштабе для обеих осей ( y относительно x ; центральный график) получается прямая линия, аналогичная той, которая получается при отображении log y относительно log x на осях с линейным масштабом ( правый график), поскольку он имеет уравнение прямой. бревно Y знак равно б ⋅ бревно Икс
Читайте также:



