Как сделать квадрат с помощью циркуля
Войти
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Реккордный квадрат
В своё время здесь размещалась информация о мастер-классе Живая Математика.
Рассматривалась задача о построении квадрата с помощью циркуля и линейки. Было предложено несколько вариантов решения. Тогда вопрос о построении с помощью минимального числа линий не ставился (но подразумевался). Однако, экстремум - это всегда интересно. В.Н.Дубровский прислал мне решение с помощью всего 8 линий. Вряд ли можно улучшить этот результат.

Начертить круг, провести диагональ. Из концов диагонали, сделать засечки, на окружности, по одну из сторон от диагонали. Провести прямую между засечками и отметить на ней середину. Провести вторую диагональ через середину этой прямой. Соединить концы диагоналей. Получится искомый квадрат
Новые вопросы в Геометрия
2. (по 2 балла за пункт) На рисунке изображён отрезок MN и отмечено несколько точек. Какие из от- меченных точек вместе с точками ми N являются вершин … ами равнобедренного треугольника? M D A
угл ABC равен 65 градусов, а угол BCD 105 градусов. Могут ли прямые АВ и CD бытьа) параллельнымиб) пересекающимися
стороны треугольника равны 12 и 15 см а биссектриса угла между ними делит 3 стороны треугольника на отрезки разность которых равна 2 см Найти пиреметр … треугольника
Построение с помощью циркуля и линейки – древнейший способ расчета в евклидовой геометрии. Известен со времен Древней Греции. Данная тема изучается в средних и старших классах на уроках геометрии.
Рассмотрим все случаи построения на конкретных примерах.
Построение отрезка, равного данному
Есть отрезок СD. Задача - начертить равнозначный данному отрезок той же величины.
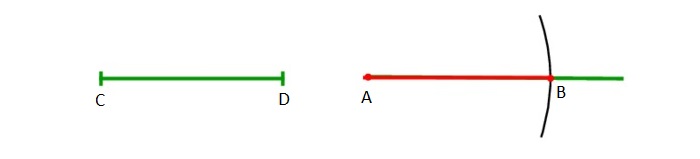
Строится луч, имеющий начало в т. A. Циркуль отмеряет существующий отрезок CD. Циркулем откладывается отрезок, равнозначный первому отрезку, на том же начерченном луче от его начала (A).
Для подобного чертежа ножку с иглой закрепляют в начале луча A, а с помощью части с грифелем проводится дуга до места соприкосновения с лучом. Данную точку можно обозначить т. B.
Отрезок AB будет равнозначен отрезку СD. Задача решена.
Деление отрезка пополам
Имеется отрезок AB.
Сначала следует нарисовать окружность с радиусом больше половины отрезка AB с центром в т. A.

Далее чертится круг с тем же радиусом с серединой в т. B. В местах пересечения окружностей имеем т. C и т. D.
Сквозь эти точки требуется провести прямую линию. Получаем т. E, которая будет серединой отрезка AB.
Построение угла, равного данному
Имеется угол ABC.
Вблизи угла проводится луч ED. Далее чертится окружность с серединой в т. B. В итоге имеем точки M и N.

Оставив раствор циркуля прежним, рисуют круг с серединой в т. E. В точке соприкосновения имеем т. K.
Поменяв раствор циркуля на длину расстояния между т. M и т. N, нужно провести окружность с серединой в т. K. В итоге получается т. F. После чертится прямая из т. E через т. F. Образуется угол DEF, который будет равнозначен углу ABC. Задача решена.
Построение перпендикулярных прямых
Пример 1
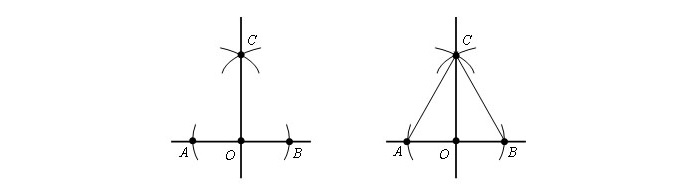
Точка O находится на прямой a.
Есть прямая и точка, находящаяся на ней. Нанести линию, идущую через существующую точку и находящуюся под прямым углом к имеющейся прямой.
Шаг 1. Чертим круг с рандомным радиусом r с серединой в т. O. Окружность соприкасается с прямой в т. A и т. B.
Шаг 2. Из имеющихся точек строится круг с радиусом AB. Точки С и D являются точками соприкосновения окружностей.
Приложив линейку, чертят прямую, сквозь т. O и одну из т. C или т. D, к примеру отрезок OC.
Доказательство, что прямая OC лежит перпендикулярно a.
Намечаются два отрезка - AC и CB. Получившиеся треугольники будут равны, согласно третьему признаку равенства треугольников. Значит, прямая CO перпендикулярна AB.
Пример 2
Точка O находится вне прямой а.
Нарисовать окружность с радиусом r из т. O. Она должна проходить сквозь прямую a. A и B — точки её соприкосновения с прямой.
Оставив прежний радиус, рисуем окружности с серединой в т. A и т. B. Точка O1 - место их соприкосновения.
Рисуем линию, соединяющая т. O и т. O1.
Доказательство выглядит следующим образом.
Две прямые ОО1 и AB пересекаются в т. C. Согласно третьему признаку равенства всех треугольников AOB = BO1A. Из данного вывода следует, что угол OAC = O1AC. Одноименные треугольники также будут равны (согласно первому признаку равенства всех треугольников).
Исходя из этого, выводим, что угол OCA = O1CA, а, учитывая смежность углов, приходим к пониманию, что они прямые. А это означает, что OC – перпендикулярный отрезок, опущенный из т. O на прямую a. Задача решена.
Построение параллельных (непересекающихся) прямых
Имеется прямая и т. А, не лежащая на этой прямой.
Нужно отметить прямую, проходящую через т. A, и параллельную имеющейся прямой.
Берется рандомная точка на имеющейся прямой и именуется B. С помощью циркуля строится окружность радиуса AB с серединой в т. B. В месте пересечения окружности и данной прямой отмечается т. C.
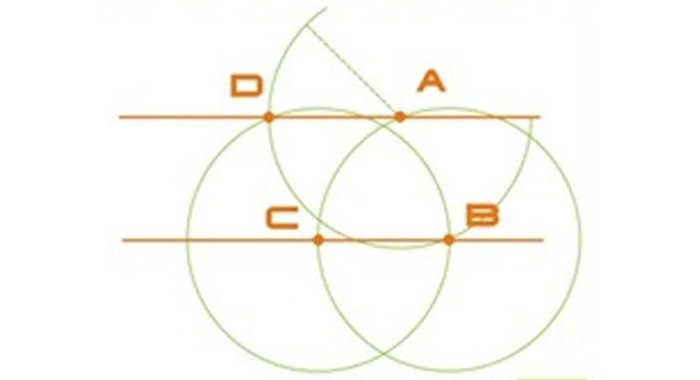
Оставив прежний радиус, рисуется еще одна окружность, теперь уже с центром в т. C. При правильных расчетах дуга должна пройти через т. B.
C тем же радиусом AB строится окружность с серединой в т. A. Точку соприкосновения второй и третьей окружностей назовем D. Третья окружность, учитывая верность расчетов, также пройдет через т. B.
Проводится прямая через т. A и т. D, которая станет параллельной первой. В итоге, получились две параллельные прямые, BC и AD.
Построение правильного треугольника, вписанного в окружность
Правила построения правильного треугольника, вписанного в окружность:
Отметить отрезок AB, чья длина будет равняться а.
Взять циркуль. Часть с иголкой расположить на т. А, а часть с карандашом на т. B. Прочертить окружность. В итоге, радиус круга будет равнозначен длине отрезка AB.

Далее иглу размещают на т. B, а часть с грифелем на т. A. Чертится круг. В итоге, его радиус будет равнозначен длине отрезка AB.
На чертеже окружности пересеклись в двух точках. Далее нужно соединить т. A и т. B и одну из вышеупомянутых точек. В результате получится равносторонний треугольник.
Стороны такого треугольника равнозначны радиусам двух окружностей, которые равны длине а. Задача решена.
Построение правильного четырехугольника вписанного в окружность
Вариант 1
Исходя из данности, что диагонали любого квадрата пересекаются в середине окружности и находятся по отношению к его осям под углом 45 градусов, производят следующие действия. Пользуясь линейкой и уголком с углами 45 градусов (см. рисунок), размечают вершины т. 1 и т. 3.
Сквозь данные точки чертят отрезки, стороны четырехугольника, расположенные по горизонтали. Это т. 4 и т. 1, т. 3 и т. 2. В конце линейкой и уголком по его катету проводятся линии, расположенные по вертикали (высоты), отрезок т.1 — т. 2 и отрезок т. 4 — т. 3.
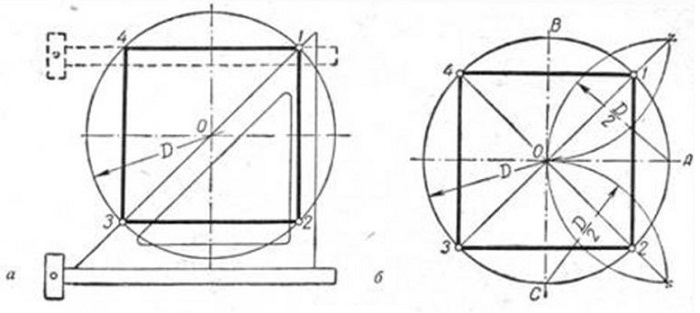
Вариант 2
Так как вершины правильного четырехугольника разделяют наполовину дуги окружностей, между точками диаметра (см. рисунок), то для достижения результата делают следующее: отмечают на точках перпендикулярных диаметров т. A, т. B и т. C и рисуют дуги до их соприкосновения.
После чертят прямые через места соприкосновения дуг, которые выделены на фигуре линиями. Точки соприкосновения с окружностью будут являться вершинами — это т. 1 и т. 3, т. 4 и т. 2. Данные вершины полученного квадрата соединяют друг с другом.
Задача выполнена двумя способами.
Построение вписанного в окружность правильного пятиугольника
Поместить на окружность т. 1, считая ее за вершину пятиугольника. Разделить отрезок AO пополам. Чтобы произвести подобную операцию, из т. A чертят дугу до места соприкосновения с окружностью в т. M и т. B.

Расположив конкретные точки на прямой, получаем т. K, и после совмещаем с т. 1. Радиусом, длина которого – отрезок А1, сделать изгиб из т. K до места соприкосновения с линией АО в т. H. После совместить т. 1 и т. H, образуя одну из пяти сторон пятиугольника.
Взять циркуль, величина раствора которого будет равна отрезку т.1 — т. H, нарисовать изгиб из т. 1 до соприкосновения с кругом. Так находят вершины 2 и 5. Отметив точки на вершинах 2 и 5, получают вершины 3 и 4. В конце все точки совмещают друг с другом.
Построение правильного шестиугольника, вписанного в окружность
Решение подобной задачи строится на свойствах, где сторона шестиугольника равнозначна радиусу круга.
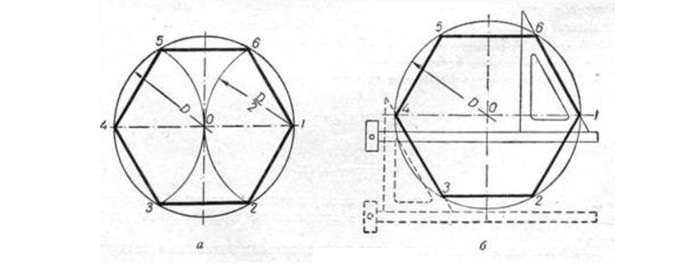
Для расчета разделяют круг на шесть ровных частей и последовательно совмещают все полученные точки (см. рисунок). Задача решена.
Итак, как нарисовать квадрат объемный поэтапно? Это не сложно, наш первый способ нарисовать объемный квадрат будет самым простым. Наша задача на этом этапе придать объем квадрату и нарисовать трехмерную фигуру на плоской поверхности бумаги. Давайте приступим!
Шаг 1: Рисуем квадрат

Начните рисовать объемный квадрат (он же куб) с простого плоского квадрата. Это будет лицевая сторона вашего объемного квадрата.
В этом пошаговом уроке вы наверняка получите хорошую практику по рисованию прямых линий)). Постарайтесь нарисовать все стороны квадрата одинаковой длины и постарайтесь, чтобы все углы квадрата были прямые - ровно 90 градусов.
Шаг 2: Добавьте боковые грани
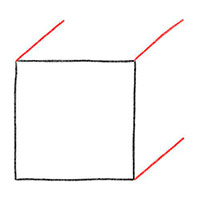
Добавьте три линии, из двух верхних углов и из нижнего правого угла квадрата. Постарайтесь нарисовать все линии одинаковой длины.
Вы можете "поиграть" с углом, под которым рисуете линии. Здесь мы провели линии примерно под углом 45 градусов. Это дает нам наиболее типичный вид Куба(объемного квадрата), на котором вы можете видеть как верхнюю, так и правую сторону куба.
Но поверните боковые линии немного больше вверх или в сторону и вы получите совершенно другие виды объемного квадрата. Просто убедитесь, что все линии имеют одинаковую длину и одинаковый угол наклона.
Шаг 3: Рисуем задние грани
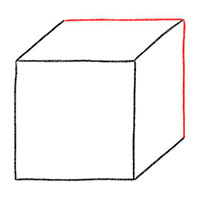
Последний этап, дорисуйте объемный квадрат, добавив последние два ребра. Они должны быть такой же длины, что и наш первоначальный квадрат. Одно ребро рисуем горизонтально (слева направо), другое вертикально (сверху вниз).
Как нарисовать объемный квадрат под разными углами

Теперь, когда вы знаете, как нарисовать объемный квадрат в базовом виде, попробуйте "поиграть" с разными углами и видами.
Перед вами полный объемный квадрат, который вы только что нарисовали. Поскольку мы продолжили угловые линии вверх и вправо, вы можете видеть верхнюю и правую стороны куба.
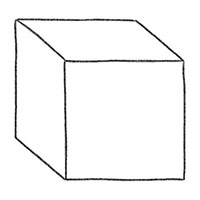
Но если вы решите продлить угловые линии вверх и влево, вы перевернете свой объемный куб таким образом, что сможете увидеть верхнюю и левую стороны куба.
Обратите внимание, что нижняя боковая линия теперь выходит из другой стороны начального квадрата.
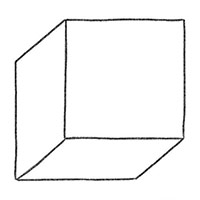
Вы можете нарисовать стороны уходящие вниз и влево и получите вид, в котором мы видим нижнюю и левую стороны объемного квадрата.
Как нарисовать объемный квадрат с одной точкой перспективы

Немного более продвинутый способ нарисовать объемный квадрат - это использовать перспективу с одной точкой схода. Получившийся объемный квадрат очень похож на тот, который мы рисовали простым способом, разница в том, что он получается чуть более сдавленным за счёт перспективы.
Не смотря на то, что рисовать такой объемный квадрат немного сложнее, результат выглядит намного более реалистично. Вот что делает перспектива, перспектива это отличный способ изобразить объемные объекты на плоской бумаге. Давайте же нарисуем наш объемный квадрат в перспективе!
Шаг 1: Нарисуйте квадрат и точку схода
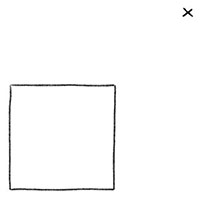
Как и в первом случае, сначала нарисуйте обычный квадрат.
Затем отметьте точку, в которую будет сливаться наша перспектива. Эта точка называется точкой схода. В нашем примере мы поместили её в правом верхнем углу, таким образом, мы получим вид объемного квадрата, который похож на тот, что мы нарисовали в примере выше.
После того, как вы нарисуете объемный квадрат так, как показано здесь, поиграйте с размещением вашей точки схода. Попробуйте переместить её подальше, вниз или влево, изменение положения точки схода даст вам совершенно другой вид вашего объемного квадрата.
Шаг 2: Обозначьте линии перспективы
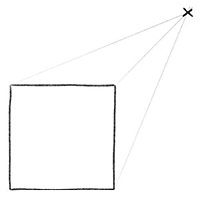
Нарисуйте линии перспективы, они послужат ориентирами для будущего объемного квадрата. Они начинаются в двух верхних и правом нижнем углу нашего переднего лицевого квадрата и сливаются в точку схода. (Эта точка называется точкой схода, так как по мере приближения к этой точке все объекты становятся меньше. В точке схода объекты будут настолько малы, что просто исчезнут.)
Чтобы вам было проще и линии получились ровные воспользуйтесь линейкой, это сильно упростить вам задачу.
Кроме того, не прорисовывайте эти линии слишком сильно – они нам нужны только в качестве ориентиров и позже мы их сотрем.
Шаг 3: Нарисуйте дальние грани объемного квадрата
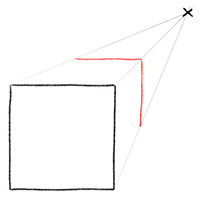
С помощью вспомогательных направляющих линий перспективы, нарисуйте дальние грани объемного квадрата.
Обе линии обозначающие задние грани объемного квадрата должны начинаться и заканчиваться на направляющих линиях перспективы. Сначала нарисуйте верхнюю дальнюю грань параллельно (в том же направлении) горизонтальной верхней линии передней грани квадрата.
Затем аналогично нарисуйте вертикальную (сверху вниз) дальнюю грань.
Да, вот несколько причудливых слов, которые вы только что узнали:
- "Параллельные" линии - это две линии, идущие в одном направлении.
- "Вертикальная" линия - это линия, идущая сверху вниз или снизу вверх.
- "Горизонтальная" линия - это линия, идущая слева направо или справа налево, такая же как и горизонт.
- А "горизонт" - это линия, где земля встречается с небом, если смотреть вдаль – линия, которая проходит ровно слева направо.
Шаг 4: Нарисуйте боковые грани, чтобы завершить объемный квадрат
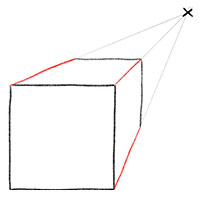
После короткого лингвистического отступления мы возвращаемся к рисованию объемного квадрата.
Следующий шаг очень простой – просто дорисуйте грани объемного квадрата проведя карандашом по вспомогательным линиям перспективы соединив его переднюю и заднюю стороны.
Шаг 5: Сотрите вспомогательные линии
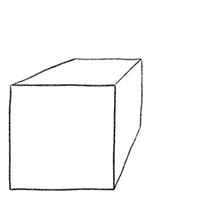
Последний этап состоит в том, чтобы стереть точку схода и вспомогательные линии, которые вы нарисовали раньше.
Как вы можете заметить, полученный рисунок объемного квадрата очень похож на простой способ, который мы использовали выше, только немного более приплюснутый сзади. Но именно это делает его более реалистичным, и он выглядит как настоящий куб в трёхмерном пространстве, хотя он и нарисован на плоской бумаге.
Как нарисовать объемный квадрат с двумя точками перспективы
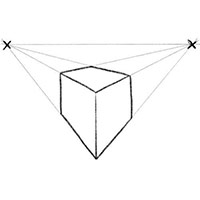
Третий способ нарисовать объемный квадрат - это способ с применением двухточечной перспективы. Он использует аналогичные рекомендации как и для случая с одной точкой перспективы, разница в том, что перспектива сходится в две разные точки. В результате получается очень динамичный и немного преувеличенно-вытянутый вид объемного квадрата, который как будто выскакивает из плоского чертежа в третье измерение.
Шаг 1: Нарисуйте две точки схода

Начнем с простого, отметив две точки схода перспективы.
Нарисуйте горизонтальную линию в верхней части листа бумаги. Затем отметьте две точки по краям, как можно дальше друг от друга. Вот так!
Чем ближе друг к другу вы расположите точки, тем более сплющенным и менее естественным будет выглядеть ваш куб(объемный квадрат), поэтому нарисуйте точки как можно дальше друг от друга, так кую будет выглядеть лучше.
После того как мы закончим рисовать этот вариант объемного куба, вы можете поэкспериментировать и попробовать сместить линию точек схода на листе бумаги вверх или вниз, так же совсем не обязательно чтобы эта линия была строго горизонтальной, её можно нарисовать как угодно, попробуйте, вам понравится!
Шаг 2: Нарисуйте переднюю грань
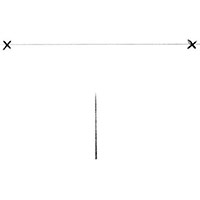
Следующий этап: нарисуйте прямую вертикальную линию – это будет передняя грань объемного квадрата. Поместите линию в середине листа бумаги, на небольшом расстоянии от горизонтальной направляющей.
Если вы сместите вертикальную линию больше влево, вы увидите больше правой стороны куба. Сместите линию вправо, чтобы увидеть больше левой стороны. Сместите линию вверх и на рисунке вы будете видеть меньше верхней части куба. А если вы проведете линию так, что она будет пересекать горизонтальную линию, то вы не увидите ни верха, ни низа вашего объемного квадрата. Понимаете, как это работает?
Шаг 3: Нарисуйте линии перспективы
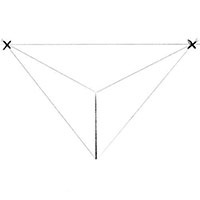
Наметьте четыре линии направления перспектив. Нарисуйте две линии из верхнего края грани нашего будущего объемного квадрата, так чтобы они соединились с точками схода.
Затем аналогично еще две линии из нижней части грани, также к точкам схода. Если у вас есть линейка, нарисуйте эти линии с помощью линейки, желательно чтобы линии получились прямые.
Шаг 4: Нарисуйте боковые грани
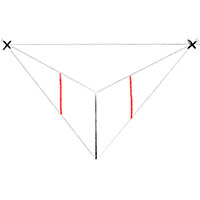
Нарисуйте две параллельные вертикальные линии, по одной с каждой стороны. Это левый и правый края объемного квадрата в двухточечной перспективе.
Шаг 5: Нарисуйте направляющие
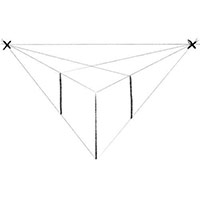
Теперь, когда у нас есть вертикальные грани нашего Куба, нарисуйте еще две направляющие обозначающие перспективу.
Они начинаются с верхних концов боковых рёбер нашего объемного квадрата. Линия от правого ребра идет к левой точке перспективы. Линия от левого ребра идет к правой точке. Таким образом, линии пересекаются создавая верхнюю сторону объемного квадрата.
Это гораздо легче увидеть на картинке, чем объяснить словами.
Шаг 6: Прорисовываем грани
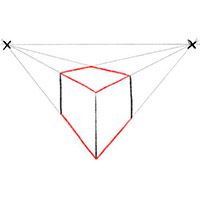
На этом этапе мы просто более чётко нарисуем все недостающие грани объемного квадрата.
Сначала прорисуйте нижние грани. Затем обведите контуром верхнюю сторону куба - четыре ребра, обозначенные пересекающимися направляющими перспективы.
Шаг 7: Сотрите вспомогательные линии
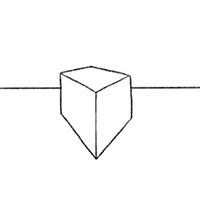
Это финальный этап. Сотрите все вспомогательные линии перспективы, чтобы полностью очистить ваш рисунок от всего не нужного. Мы также добавили горизонтальную проходящую линию за нашим объемным квадратом - она создаст эффект того, что куб как бы лежит на столе или какой-то другой поверхности.
Вот и все – теперь вы умеете рисовать объемный квадрат в 2-х точечной перспективе. Как видите, результат получился очень даже динамичным и выразительным.
Если вы хотите, чтобы нижний угол выступал меньше и выглядел немного более естественно, просто нарисуйте центральное ребро куба (самую первую вертикальную толстую линию) выше и ближе к горизонту. Ну а дальше все поэтапно начиная с шага №2.
Читайте также:


