Как сделать квадрат из числа

Обновлено: 23.01.2025

Несколько рекомендаций как быстро и просто возвести числа в квадрат (умножить число само на себя).

Вариант 1. Двухзначное число, заканчивающееся на 5

Например, найдем квадрат числа 35

Шаг 1: Умножьте первую цифру числа на цифру, которая стоит выше в ряду с ней: 3 х 4 = 12

Шаг 2: К числу, которое получилось припишите в конце число 25 .

Ответ: 1225

Вариант 2. Любое двухзначное число

Например, найдем квадрат числа 47

Шаг 1: Возьмем ближайшее число, кратное 10. В нашем примере это число 50 Разница составит 3

Шаг 2 : Теперь найдем нижнее число с разницей 3 от нашего числа. В нашем примере 47 — 3 = 44

Шаг 3: Умножим два полученных одно на второе. 44 х 50 = 2200

Шаг 4: Находим квадрат нашей разницы 3, квадрат 3 = 9

Шаг 5: Прибавляем число полученное в шаге 5 к числу шага 4. 2200 + 9 = 2209 .

Ответ: 2209

При желании всегда быстро общаться, обмениваться мнениями или просто болтать можно просто скачать аську и наслаждаться общением. Аська самый простой и быстрый способ онлайн общения

Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей.

В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.

Квадрат суммы и квадрат разности

Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:

Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:

Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.

Квадрат близкий к известному квадрату

Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:

На 1 больше:

Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.

31 2 = 30 2 + 31 + 30 = 961
16 2 = 15 2 + 15 + 16 = 225 + 31 = 256

На 1 меньше:

Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.

19 2 = 20 2 – 19 – 20 = 400 – 39 = 361
24 2 = 25 2 – 24 – 25 = 625 – 25 – 24 = 576

На 2 больше

Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.

22 2 = 20 2 + 2*(20+22) = 400 + 84 = 484
27 2 = 25 2 + 2*(25+27) = 625 + 104 = 729

На 2 меньше

Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.

48 2 = 50 2 – 2*(50+48) = 2500 – 196 = 2 304
98 2 = 100 2 – 2*(100+98) = 10 000 – 396 = 9 604

Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).

Квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.

15 2 = (1*(1+1)) 25 = 225
25 2 = (2*(2+1)) 25 = 625
85 2 = (8*(8+1)) 25 = 7 225

Это верно и для более сложных примеров:

Квадрат чисел близких к 50

Считать квадрат чисел, которые находятся в диапазоне от 40 до 60, можно очень простым способом. Алгоритм таков: к 25 прибавляем (или вычитаем) столько, насколько число больше (или меньше) 50. Умножаем эту сумму (или разность) на 100. К этому произведению добавляем квадрат разности числа, возводимого в квадрат, и пятидесяти. Посмотрите работу алгоритма на примерах:

44 2 = (25-6)*100 + 6 2 = 1900 + 36 = 1936
53 2 = (25+3)*100 + 3 2 = 2800 + 9 = 2809

Квадрат трехзначных чисел

Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:

Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:

436 2 = (400+30+6) 2 = 400 2 + 30 2 + 6 2 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096

Тренировка

Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.

Для возведения числа в квадрат в Excel можно использовать функцию степени, которая представлена символом крышки (^). Используйте формулу =N^2,в которой N — это число или значение ячейки, которую нужно квадратить. Эту формулу можно использовать несколько раз на всем протяжении всего таблицы.

Возведение в квадрат числа в отдельной ячейке

Щелкните внутри ячейки на листе.

Введите в ячейку =N^2, где N — это число, которое нужно возвести в квадрат. Например, чтобы вставить в ячейку A1 квадрат числа 5, введите в нее =5^2.

Нажмите клавишу ВВОД, чтобы получить результат.

Совет: Для этого вы также можете щелкнуть другую ячейку.

Возведение в квадрат числа в другой ячейке

Щелкните внутри ячейки и введите нужное число.

Вы можете выбрать другую пустую ячейку на одном из них.

Введите =N^2 в пустую ячейку, в которой N — это ссылка на ячейку, содержаща числовую величину, которую нужно квадратить. Например, чтобы отобразить квадрат значения в ячейке A1 в ячейке B1, введите =A1^2 в ячейку B1.

Нажмите клавишу ВВОД, чтобы получить результат.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

Тренажер создан для помощи старшекласникам, для изучения или повторения возведения целого числа в квадрат в режиме реального времени. Главная цель - закрепить навыки в обработке вычислительных действий возведения целого числа в квадрат. Имеется три уровня сложности. Первый уровень - числа до 10. Второй уровень - числа от 10 до 20. Третий уровень от 20 до 33. Найдите квадрат числа и введите правильный ответ.

ТАБЛИЦА КВАДРАТОВ натуральных чисел от 0 до 100.

ЕДИНИЦЫ
0²	1²	2²	3²	4²	5²	6²	7²	8²	9²
0	0	1	4	9	16	25	36	49	64	81
1	100	121	144	169	196	225	256	289	324	361
Д	2	400	441	484	529	576	625	676	729	784	841
Е	3	900	961	1024	1089	1156	1225	1296	1369	1444	1521
С	4	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
Я	5	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
Т	6	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
К	7	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
И	8	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Возведение в квадрат двухзначных чисел.

Первый способ

Пример 1:

Нужно разложить 32 на два числа, чтобы одно число было круглым. Чтобы получилось круглое число нужно из 32 вычесть 2 получится 30.Чтобы получить второе число нужно к 32 прибавить 2 получится 34. То есть нужно вычитать и прибавлять одинаковое число. Умножаем 30 на 34 получается 1020, и прибавляем число которое вычитали и прибавляли в квадрате, то есть 2² = 4, получится 1024.

Пример 2:

Нужно разложить 47 на два числа, чтобы одно число было круглым. Чтобы получилось круглое число нужно к 47 прибавить 3 получится 50. Чтобы получить второе число нужно из 47 вычитать 3 получится 44. Умножаем 50 на 44 получается 2200, и прибавляем число которое вычитали и прибавляли в квадрате, то есть 3² = 9, получится 2209.

Второй способ

Возведение в квадрат двухзначных чисел через формулу

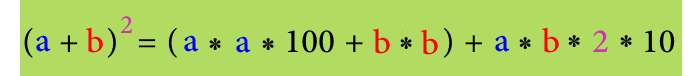
Пример:

Возведём в квадрат число 37. Для этого разложим число 37 на цифры 3 и 7, воспользуемся формулой для решения.
3 7 2 = ( 3 * 3 * 100 + 7 * 7 ) + 3 * 7 * 2 * 10 = 949 + 420 = 1369

В этой статье мы поговорим, что такое квадрат числа, как его найти, а также каким образом производятся подобные вычисления в программировании.

Квадратом Х называют произведение 2-х множителей, каждый из которых равен Х.

Если говорить еще более простым языком, то квадратом можно назвать число, которое умножено само на себя. Таким образом, мы можем написать простейшую формулу вычисления Х 2 :

Почему вообще такое выражение называют квадратом X? Дело в том, что именно данной формулой выражают площадь квадрата, сторона которого равна X, то есть геометрически это значение можно представить в виде площади квадрата, имеющего целочисленную сторону.

Вывод тут прост: для решение поставленной задачи следует требуемое значение взять в качестве множителя дважды, а потом вычислить произведение. Соответственно:

10 2 = 10 ⋅ 10 = 100

Это все элементарно и проходится в начальных классах средней школы. Решить такой пример в математике не проблема, а когда числовые значения выходят за рамки классической таблицы умножения, используют таблицу, ускоряющую расчеты.

Также описанную математическую операцию можно рассматривать в контексте частного случая возведения в степень — ведь именно этим, по сути, она и является — возведением в степень 2.

Интерес представляет и числовая последовательность для квадратов целых чисел, являющихся неотрицательными (речь идет о последовательности A000290 в OEIS):

Нельзя не сказать и про график y=x², где представлены целые значения x на отрезке 1-25.

Квадратные числа

Легко понять, что сто — это квадратное число, так как его можно записать в виде 10 ⋅ 10 , плюс оно может быть представлено, как было сказано выше, в качестве площади квадрата со стороной, равной десяти. Таким образом, можно сделать вывод, что квадратное число включено в категорию классических фигурных чисел, то есть чисел, которые мы можем представить в виде геометрических фигур. Но в эту тему углубляться пока не будем.

А что в программировании?

Теперь давайте посмотрим, как все это работает в программировании. Для примера возьмем такой язык программирования, как Java (кстати, статья о том, как выполнять возведение в степень в Java, уже была).

Напишем простой метод по возведению любых числовых значений в квадрат:

public class Main

static int square(int x)

public static void main(String[] args)

Вы можете воспользоваться любым онлайн-компилятором для проверки этого кода. Также никто не мешает вписать любое число вместо десяти.

Теперь воспользуемся простейшей программой для того, чтобы найти квадратный корень из 100:

public class Main

public static void main(String args[])

System.out.printf("sqrt(%.2f) = %.2f%n", x, Math.sqrt(x));

Программа позволяет извлекать корень и из неквадратных значений. Ниже мы находим корень из 167:

Да, в современную эпоху калькуляторов мало кто считает в уме. Вдобавок ко всему, сегодня даже не надо покупать настоящий калькулятор, так как калькулятор есть в любом мобильном телефоне, не говоря уже об онлайн-калькуляторах, коих существует огромное количество. Однако это не значит, что можно забыть азы алгебры. Не зря же великий русский ученый Михаил Ломоносов когда-то сказал:

Читайте также: