Как сделать квадрат 5 на 5 см
Рассмотрим следующий геометрический парадокс. Возьмём квадрат со с стороной 8 см и разрежем его как показано на рисунке1, а затем сложим из полученных частей пря-моугольник Получившийся прямоугольник имеет размеры 5 на 13. как показано на рисунке 2. Давайте теперь сравним площади полученных фигур. Т.к. эти две фигуры составлены из одинаковых кусков, то и площади этих фигур должны быть равны. Давайте сравним их:
Давайте теперь сравним площади полученных фигур. Т.к. эти две фигуры составлены из одинаковых кусков, то и площади этих фигур должны быть равны. Давайте сравним их: Sквадрата=8*8=64 см2 Sпрямоугольника=5*13=65 см2 т.е. мы получаем, что6 4=65 Этот "парадокс" кажется неразрешимым. Действительно, трудно представить, что "извне" возникла "лишняя" единица! Оказывается, что длины сторон четырех частей, составляющих фигуры (рис. 1 и 2), являются членами ряда Фибоначчи. Расположение частей, на которые был разрезан квадрат, в виде прямоугольника иллюстрирует одно из свойств ряда Фибоначчи, а именно следующее: при возведении в квадрат любого члена этого ряда получается произведение двух соседних членов ряда плюс или минус единица. В нашем примере сторона квадрата равна 8, а площадь равна 64. Восьмерка в ряду Фибоначчи расположена между 5 и 13. Так как числа 5 и 13 становятся длинами сторон прямоугольника, то площадь его должна быть равной 65, что дает прирост площади в одну единицу. Благодаря этому свойству ряда можно построить квадрат, стороной которого является любое число Фибоначчи, большее единицы, а затем разрезать его в соответствии с двумя предшествующими числами этого ряда. Если, например, взять квадрат в 13х13 единиц, то три его стороны следует разделить на отрезки длиной в 5 и 8 единиц, а затем разрезать, как показано на рис. 2. Площадь этого квадрата равна 169 квадратным единицам. Стороны прямоугольника, образованного частями квадратов, будут 21 и 8, что дает площадь в 168 квадратных единиц. Здесь одна квадратная единица не прибавляется, а теряется.
Этот парадокс объясняется тем, что точки A, B, C, D на рисунке на самом деле не лежат на одной прямой, а являются вершинами параллелограмма, площадь которого как раз и равна "лишней" единиц
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
 |
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
      |
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
Из равенства (1) найдем d:
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
 |

Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
 |
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
 |

Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
 |

Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
 |
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
Из формулы (5) найдем R:
 |

или, умножая числитель и знаменатель на , получим:
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
 |

Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 |

Пример 5. Радиус описанной вокруг квадрата окружности равен Найти сторону квадрата.

Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя в (8), получим:
 |

Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:

где − сторона квадрата.

Пример 6. Сторона квадрата равен . Найти периметр квадрата.

Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя в (9), получим:
 |

Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.

Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
 |
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
Так как AD и BC перпендикулярны, то
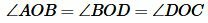 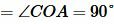 | (11) |
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
Эти реугольники также равнобедренные. Тогда
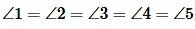 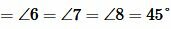 | (13) |
Из (13) следует, что

Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
Можно ли разрезать квадрат на несколько частей так, чтобы потом их них можно было составить два квадрата, длины сторон которых выражаются целым числом сантиметров, если сторона данного квадрата равна:
1 ) 5 см;
2 ) 6 см?
Решение 1
, поэтому если сторона квадрата равна 5 см, то его можно разрезать на квадраты со стороной 1 см, затем сложить два квадрата, длина сторон которых равны 3 см и 4 см.
Решение 2
Если стороны квадрата равны 6 см, то его невозможно разрезать на несколько частей так, чтобы потом из них можно было бы сложить два квадрата с целочисленными длинами, так как

Надо из 8 спичек сложить 3 квадрата. При этом спички ломать нельзя. Ответ: Ломать спички нельзя, но про наложение спичек друг на друга ничего не указано. Поэтому получаем 2 квадрата со стороной в 1 спичку и один со стороной в половину спички. См. рисунок:
Загадка для детей №4142.
На столе лежат три кучки из 11, 7 и 6 спичек. Перекладывая спички из любой кучки в любую другую, нужно сделать так, чтобы в каждой было по 8 спичек. При этом к любой кучке разрешается добавлять ровно столько спичек, сколько в ней уже есть. Задача решается в три хода. Ответ: 1. Перемещаем 7 спичек из первой во вторую кучку: (4, 14, 6) 2. Перемещаем 6 спичек из второй кучки в третью: (4, 8, 12) 3. Перемещаем 4 спички из третьей в первую кучку: (8, 8,
Из спичек выложено неверное равенство 6*8=64. Надо убрать 2 спички так, чтобы равенство стало верным. Ответ: Ответ на рисунке – из восьмерки делаем девятку, а из шестерки пятерку.
Загадка для детей №4068.
Из спичек построен дом. Переложить две спички так, чтобы дом повернулся другой стороной. Ответ: на рисунке

Из шести спичек составить четыре равных равносторонних треугольника. Ответ: Можно смело поручиться, что мало кому сразу придёт в голову решение этой простой задачи. Дело в том, что в данном случае приходится строить из спичек не плоскую фигуру, а фигуру в пространстве. Положите на стол три спички так, чтобы они составляли треугольник, затем поставьте остальные три спички так, чтобы они нижними своими концами упирались в углы лежащего на столе треугольника, а верхними концами соединялись вместе над его серединою. В результате у вас получится треугольная пирамида, все грани которой являются равными между собой равносторонними треугольниками. Загадка для детей №4108.
Из спичек сложена фигура, похожая на детскую игрушку – неваляшку. Вам нужно переложить на другое место три спички, чтобы неваляшка превратилась в куб. Ответ: На картинке
Загадка для детей №4058.
Нужно переложить одну спичку так, чтобы получилось верное равенство. Ответ: на рисунке
Загадка с подвохом №4062.

Из семи спичек выложено число 1/7. Превратите эту дробь в число 1/3, не прибавляя и не убавляя спичек.
Ответ: на рисунке

Загадка для детей №4064.
Ответ: на рисунке

Загадка для детей №4107.

Из спичек сложен правильный пятиугольник. Добавьте к нему ещё пять спичек, чтобы получилось два правильных пятиугольника и пять равнобедренных треугольника.
Материалы по теме Супермодели, которые погрузились в бедность
Ответ: На картинке

Загадка для детей №5275.

Переложите 3 спички так, чтобы получилось 3 квадрата.
Ответ: На рисунке.

Загадка для детей №4075.

Из спичек сложена объёмная фигура, состоящая из 4 кубов. Сделай так, чтобы кубов стало три, переложив всего 1 спичку.
Ответ: на рисунке

Загадка для детей №5273.

Как из 3 спичек, не ломая их, сделать четыре? Ответ: Нужно выложить римскую цифру 4.
Загадка для детей №4057.
Этот храм построен из одиннадцати спичек. Требуется переложить четыре спички так, чтобы получилось пятнадцать квадратов. Ответ: на рисунке
Загадка для детей №4940.
Загадка для детей №4065.
Из 12 спичек выложено 4 одинаковых квадрата. Требуется, переложив 2 спички, образовать 7 квадратов. Ответ: на рисунке
Загадка для детей №4054.
Из спичек сложена фигура, изображённая на рисунке. Как переложить две спички так, чтобы получилось ровно четыре одинаковых квадрата с длиной стороны, равной длине спички? Ответ: на рисунке
Загадка для детей №4067.
Приложить к четырём спичкам пять спичек так, чтобы получилось сто. Нужно найти два решения. Ответ: на рисунке
Загадка для детей №4055.

Спичечный рак ползёт вверх. Переложить три спички так, чтобы он пополз вниз.
Ответ: на рисунке

Загадка для детей №4066.

Переложите одну спичку так, чтобы получилось верное равенство. P.S. Существует два решения этой задачи. Постарайтесь найти оба.
Ответ: на рисунке

Загадка для детей №4069.

Весы составлены из девяти спичек и не находятся в состоянии равновесия. Требуется переложить в них пять спичек так, чтобы весы оказались в равновесии.
Ответ: на рисунке

Загадка для детей №5274.
Переложите 4 спички так, чтобы получилось 2 квадрата. Ответ: Выньте четыре спички из середины фигуры и постройте из них новый квадрат.
Загадка для детей №4059.
Переложить в фигуре, показанной на рисунке, пять спичек так, чтобы получилось три квадрата. Ответ: на рисунке
Загадка для детей №7947.
Переложите одну спичку так, чтобы верное равенство – осталось верным. Ответ: 05+40=45
Загадка для детей №4063.

Переложив четыре спички, превратить топор в три равных треугольника.
Ответ: на рисунке

Загадка для детей №4071.
Ответ: на рисунке

Загадка с подвохом №4073.
Положить шесть спичек так, чтобы образовался квадрат.
Ответ: Нужно две спички надломить посередине.

Загадка для детей №4056.

Фигура, изображённая на рисунке, составлена из восьми спичек, наложенных друг на друга. Снять 2 спички так, чтобы осталось 3 квадрата (прямоугольники не считаются).
Ответ: на рисунке

Загадка с подвохом №5276.
Как из 13 целых спичек, каждая из которых в 5 сантиметров длиною, положенных одна около другой, составить метр?

Загадка для детей №4061.

Две рюмки составлены из десяти спичек. Переложить шесть спичек так, чтобы получился дом.
Ответ: на рисунке

Как сделать квадрат из карандашей
Этот способ сложнее, сложнее тем что нужно будет еще доказать что вы правы. Наверное, каждый из вас знает что 2*2 это 4,то есть 2 в квадрате ровно 4. Главное, чтобы оппонент не понял, что 1+1+1+1 тоже равно 4.Вот пример на фото.

Как сделать квадрат из 3 карандашей. Способ 2
Видео
: играют малыши
Малыши 2-3 лет едва ли будут ломать голову над задачей о том, как сделать из квадрата….. Им нужны игры другого рода, а именно выкладывание фигур, предметов, а еще лучше сказки из спичек.
Нам было комфортно играть за низким журнальным столиком (он отведен у нас для детского творчества и игр). Итак, высыпаем несколько пачек спичек на середину и начинаем рассказ. Например, такой:

У него был свой домик

Однажды он встретил змею

Змея жила в густой траве

И так далее: расскажите о том, как они подружились, встретили лошадку, человека, пытались залезть на дерево и почему у ежика это не получилось. Ребенок обязательно втянется, если его не трогать, а просто интересно творить, рассказывать и строить. Пройдет немного времени и уже вы будите слушать сказки в исполнении малыша =)
Играть
Несмотря на то что головоломки со спичками являются отличным способом проверить смекалку, они с каждым годом все реже и реже применяются. Можно сказать, чем менее популярными становятся спички (которым на смену приходят более современные средства добычи огня), тем быстрее теряют популярность спичечные игры и задачки.
Однако в последнее время они начинают приобретать былую популярность благодаря интернету и онлайн играм. Сыграть в несколько игр со спичками вы можете по данной ссылке.
Читайте также:


