Как сделать круг в квадрате

Задачу можно решить даже не зная где находится центр. Т. е. вам задана уже готовая окружность и центр не указан.
Чтобы отметить вершины квадрата с помощью одного циркуля, сначала рисуют круг. Затем зафиксировав раствор циркуля и начав с любой произвольно взятой на окружности точки А, отмечают точки B, C и D. Из точек А и D как из центров раствором АС проводят две дуги, которые пересекаются в точке Е. Расстояние ЕО равно стороне искомого квадрата. Следовательно, если мы сделаем из А засечки F и G радиусом ОЕ, то A,F,D,G будут вершинами квадрата.
Есть в учебнике. Ставишь центр. Проводишь окружность. Вспоминаешь главное свойство квадрата - равенство всех сторон и углов. Не меняя раствора циркуля ставишь иглу на окружность и проводишь еще одну окружность. Соединяешь точки пересечения окружностей прямой - это сторона квадрата. Переносишь иглу цикруля на это пересечение - новая окружность - новая сторона. И так достраиваешь.
Собственно, есть квадрат произвольного размера.
В него необходимо вписать окружность диаметром равную стороне квадрата и все, что вне окружности - закрасить в черный цвет.
Есть ли тому относительно простой способ.
Оценить 13 комментариев
есть квадрат произвольного радиуса = это, однозначно, прорыв.
Если квадрат в итоге все равно будет черным, что мешает его сразу закрасить и отрисовать в нем окружность?


D' Normalization: в принципе, по контексту фразы можно было бы и понять, что именно имелось ввиду. Хотя, конечно, проявить остроумие - это так круто и весело.
- Нарисовать сплошной черный квадрат.
- Нарисовать сплошной белый круг поверх него.
- (по уточненным условиям задачи) Использовать полученное однобитное изображение в качестве маски для исходного изображения. Есть много вариантов реализации этого.
есть квадратная матрица данных, визуализирующаяся изображением.
изображение должно быть круглым.
но так исторически сложилось, что оно было квадратным физически и прозрачным вне окружности.
печаль в том, что матрица теперь может быть любого размера, поэтому просто захардкодить области невидимости не выйдет.

nirvimel: есть данные.
размером, например, 100 строк по 100 значений, каждое значение выводится в виде точки определенного цвета.
надо их вывести в виде картинки, где все, что внутри окружность радиусом 100 - остается как есть, а все, что вне окружности - перекрашено в черный цвет.

D' Normalization: м.. если Вам важен Ваш вклад - напишите это ответом на вопрос, чтобы я мог пометить его решением.
Анализируя различные положения квадрата и окружности относительно точки зрения и линии горизонта а также правила их изображения в перспективе легко обнаружить общие закономерности. Геометрическая связь этих фигур определяется тем, что вокруг любой окружности можно описать квадрат, а также в любой квадрат можно вписать окружность.
Как вписать окружность в квадрат?
Рассмотрите рисунок 48. Квадрат и вписанная в него окружность имеют общий центр - точку пересечения диагоналей квадрата. Окружность касается сторон квадрата в точках 1,2,3,4.Точки касания делят стороны квадрата пополам. Для того чтобы изобразить вписанную в квадрат окружность (в перспективном рисунке - эллипс) необходимо определить положение осей эллипса и найти точки, задающие его размеры (точки 1 - 4).
 |
Горизонтальный квадрат.
Найдите точки касания на перспективном рисунке горизонтально расположенного квадрата (рис.49): для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода.
Окружность, лежащая в горизонтальной плоскости, изображается в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию - малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис.50). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1,2,3,4. Проверьте симметричность полученного эллипса относительно его осей (рис. 51).
 |
 |
| Рис.50 |

перспективный рисунок простых геометрических тел
Вертикальный квадрат.
При вертикальном положении квадрата точки 1,2,3,4найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис.52). Несколько сложнее определить направление осей эллипса. Для решения этой задачи представьте, что изображаемый нами эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 53). Ось цилиндра всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Ее направление можно найти, опираясь на знание и опыт рисования куба, или взять с натуры, если таковая имеется. Таким образом, мы определили положение малой оси эллипса. А большая ось будет ей перпендикулярна и пройдет через точку, смещенную от пересечения диагоналей - центра окружности - ближе к зрителю (рис.54). На двух осях и по четырем точкам сначала наметьте эллипс легкими линиями, а затем уточните рисунок (рис.55).
Заметим, что эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и исправлений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним. Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе, поэтому задачу грамотного изображения квадрата современная методика рисования предлагает решать с помощью эллипса, вокруг которого описывается квадрат.
В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).
Содержание:

Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).
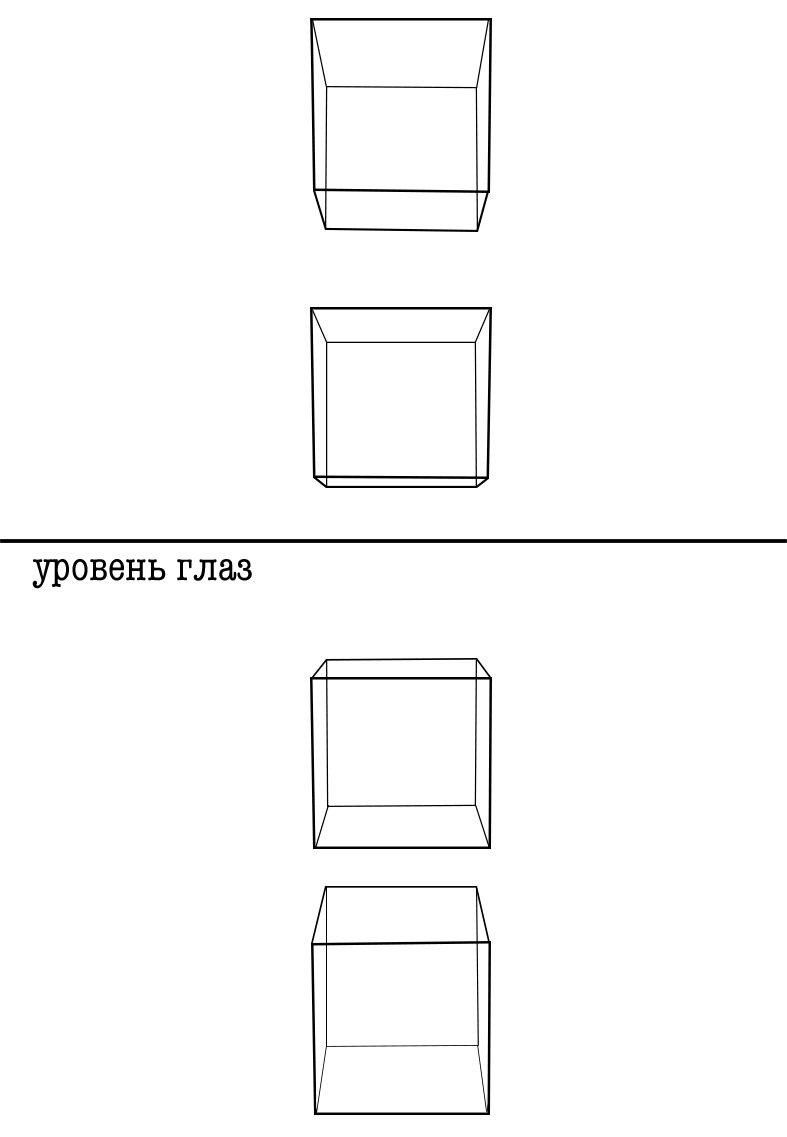
То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.

Принципы рисования эллипсов:
Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.

Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).

Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).
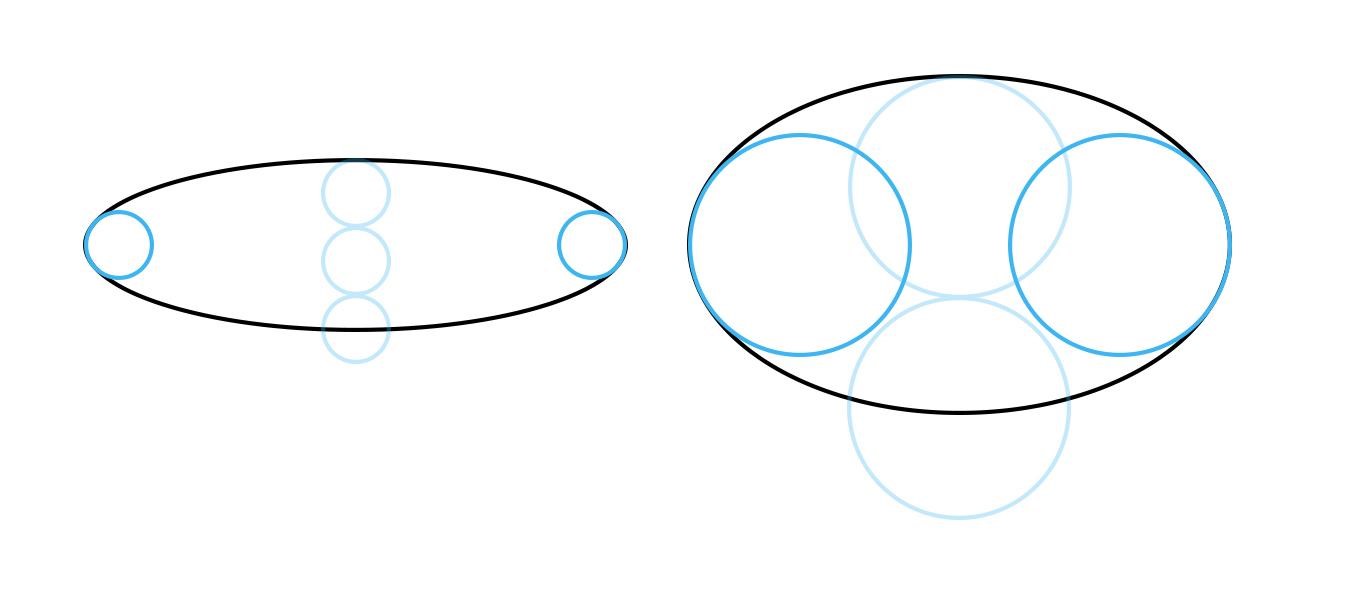
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.
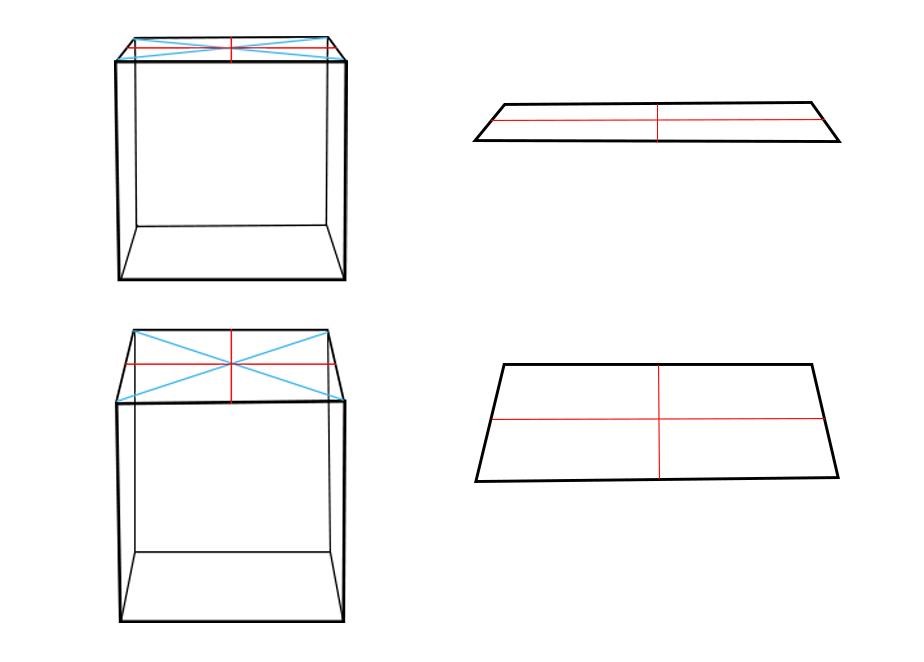
Рисуем эллипсы
Шаг 1. Для начала проведем две перпендикулярных оси.
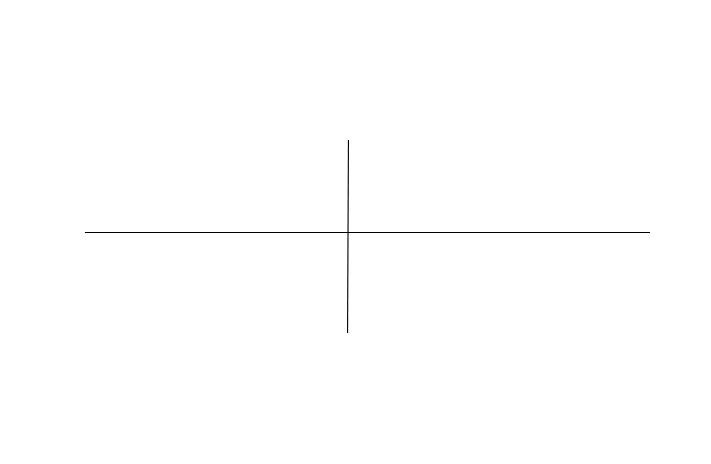
Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.
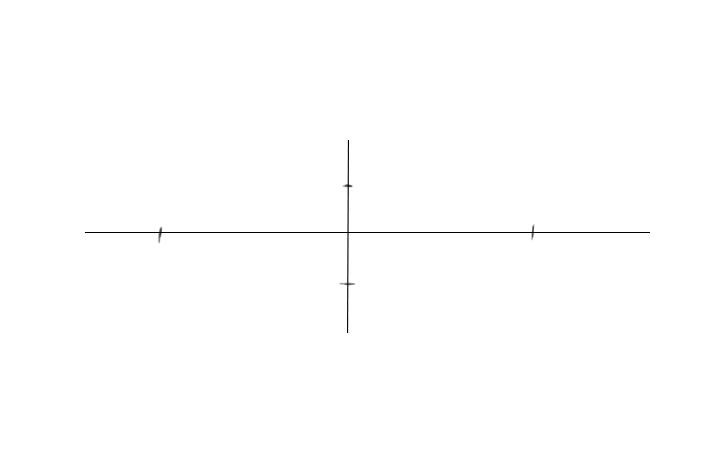
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.
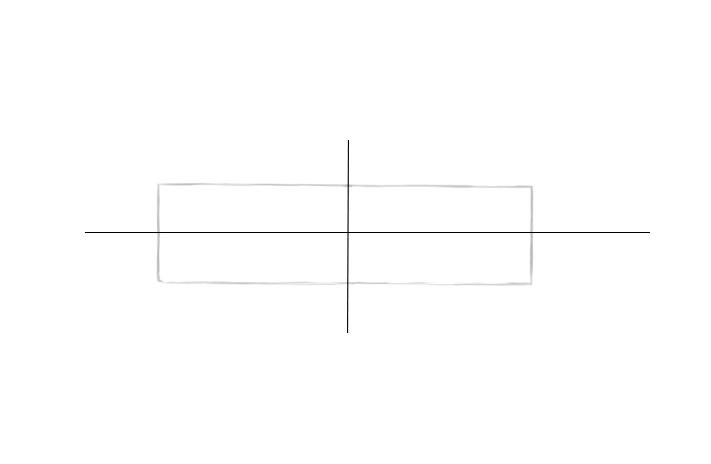
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.
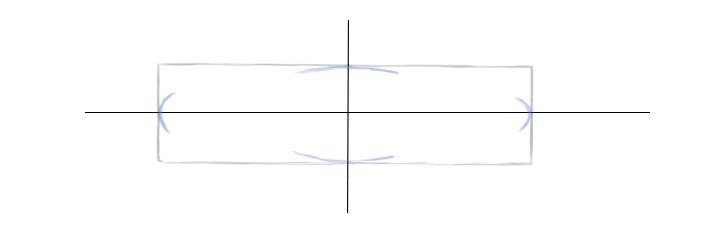
Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.
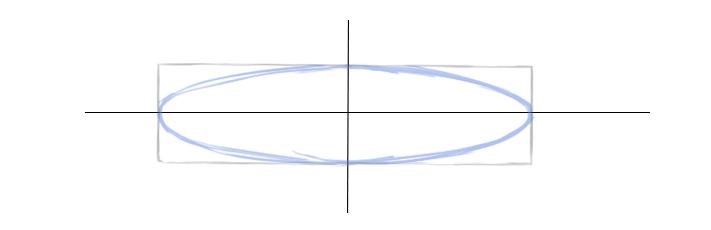
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.
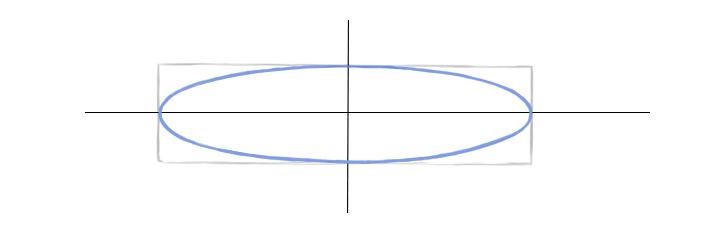
Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.
Рисуем кружку

Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.

Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.
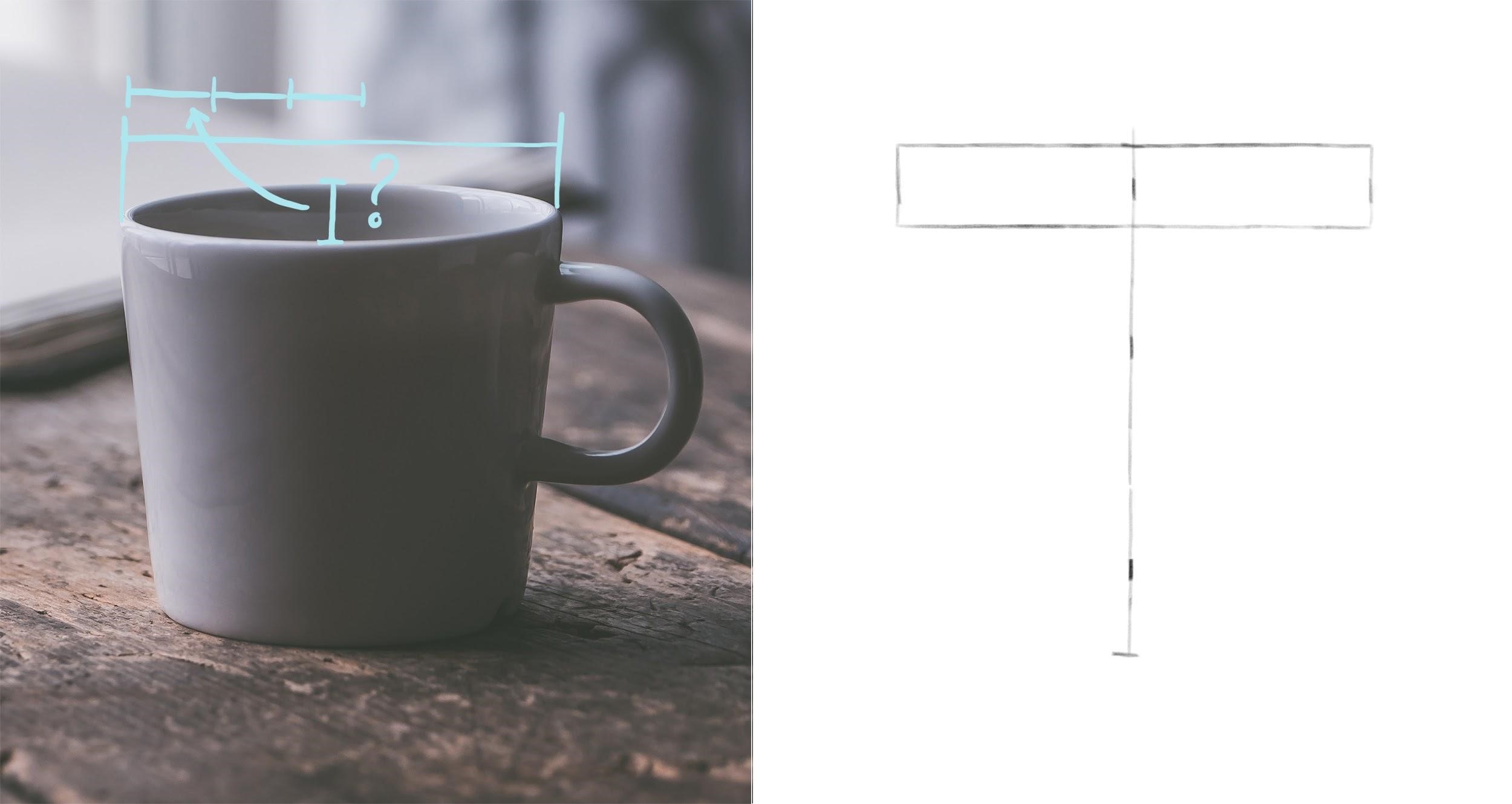
Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.
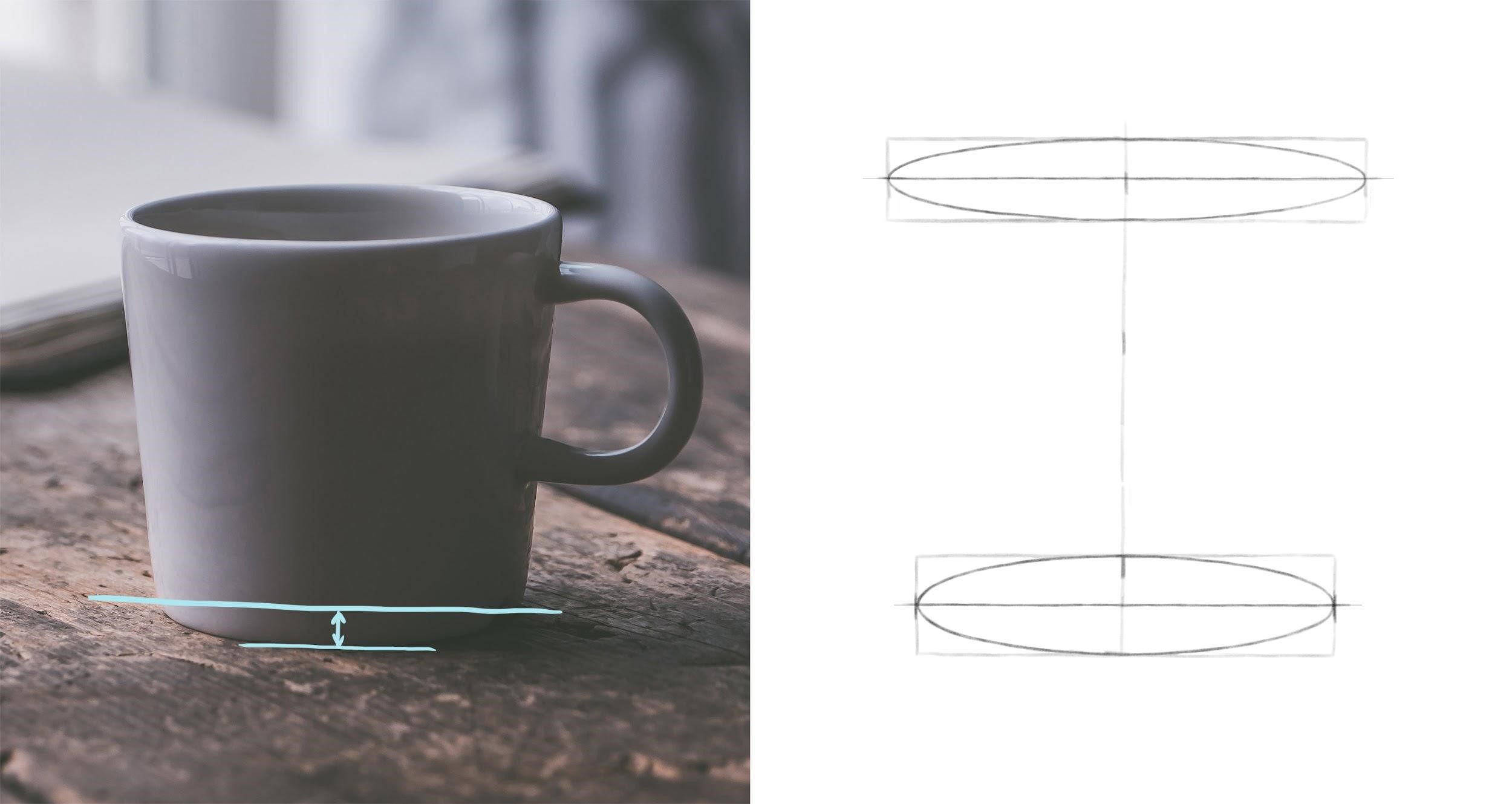
Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.

Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то - на глаз).

Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!

Рисуем вазу
В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.
В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).

Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.
Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.
Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).
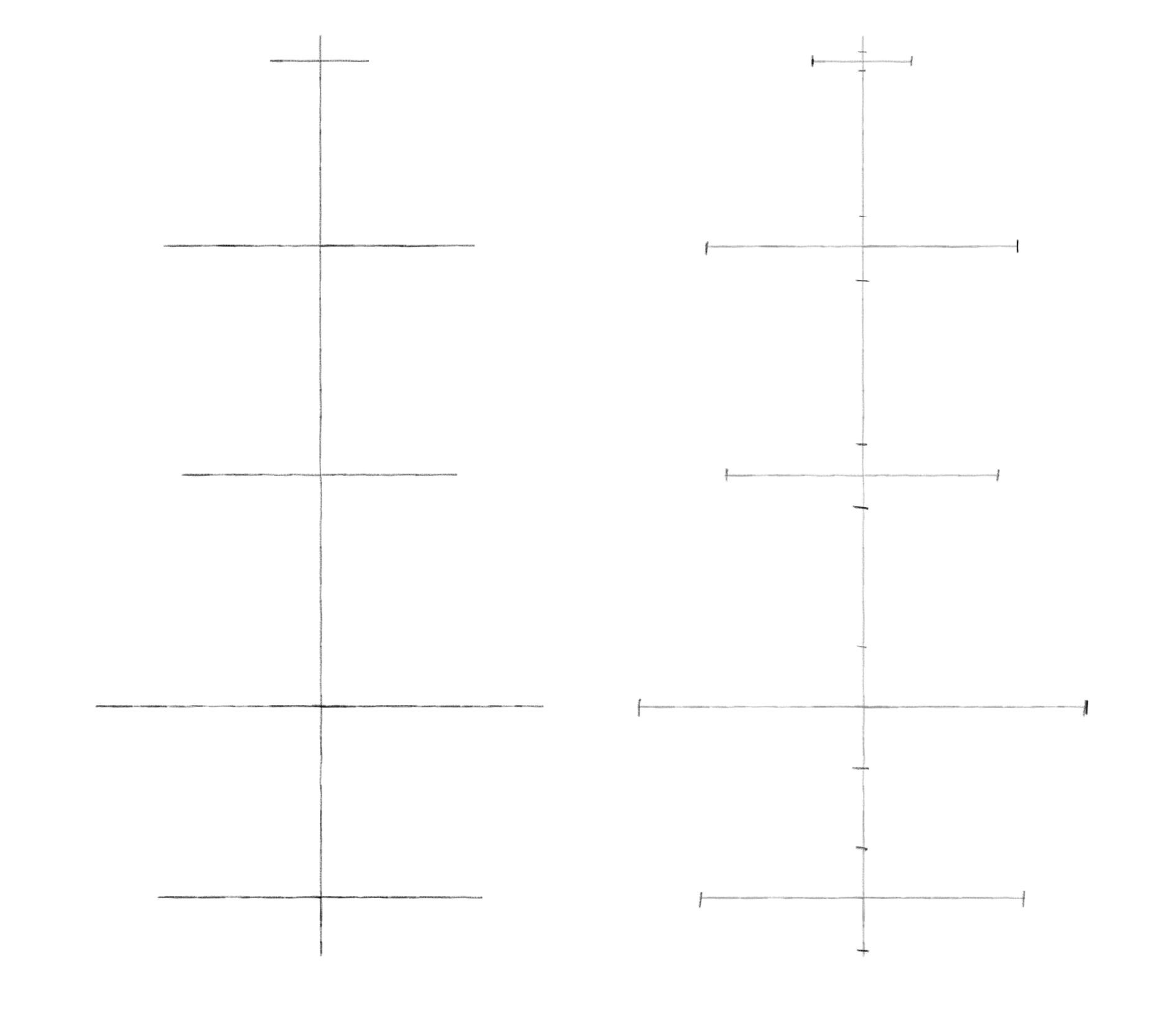
Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.
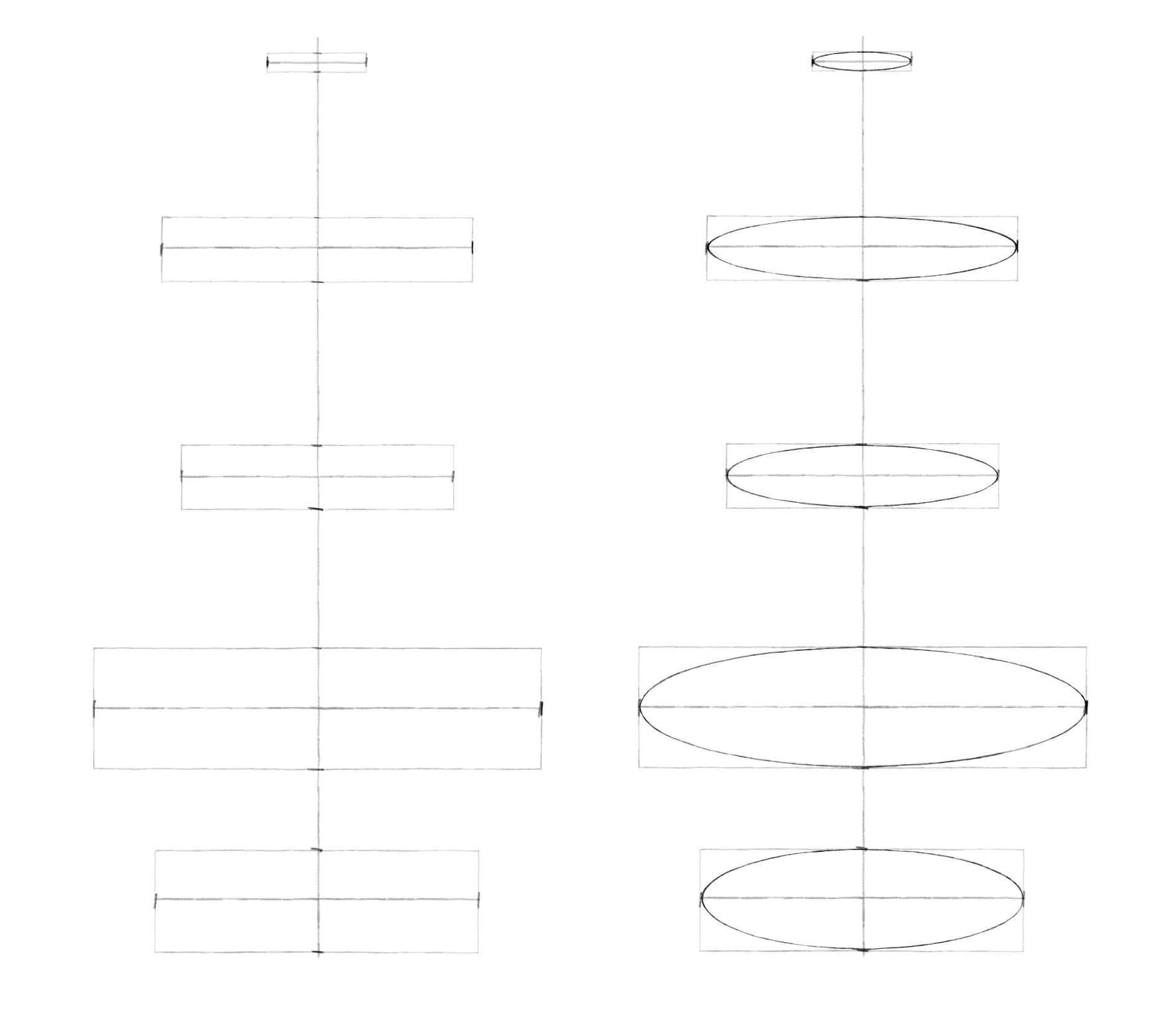
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.
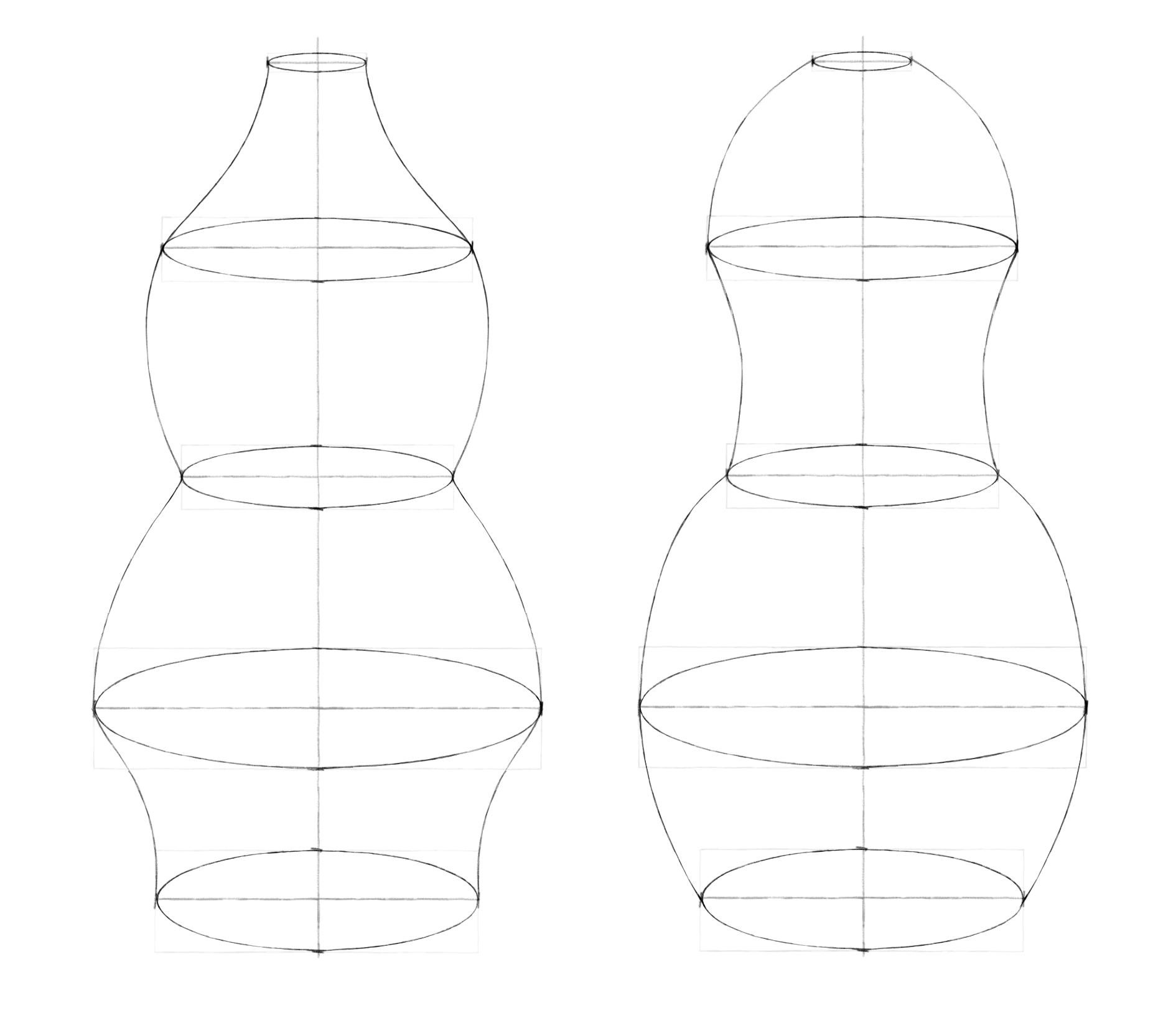
Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!
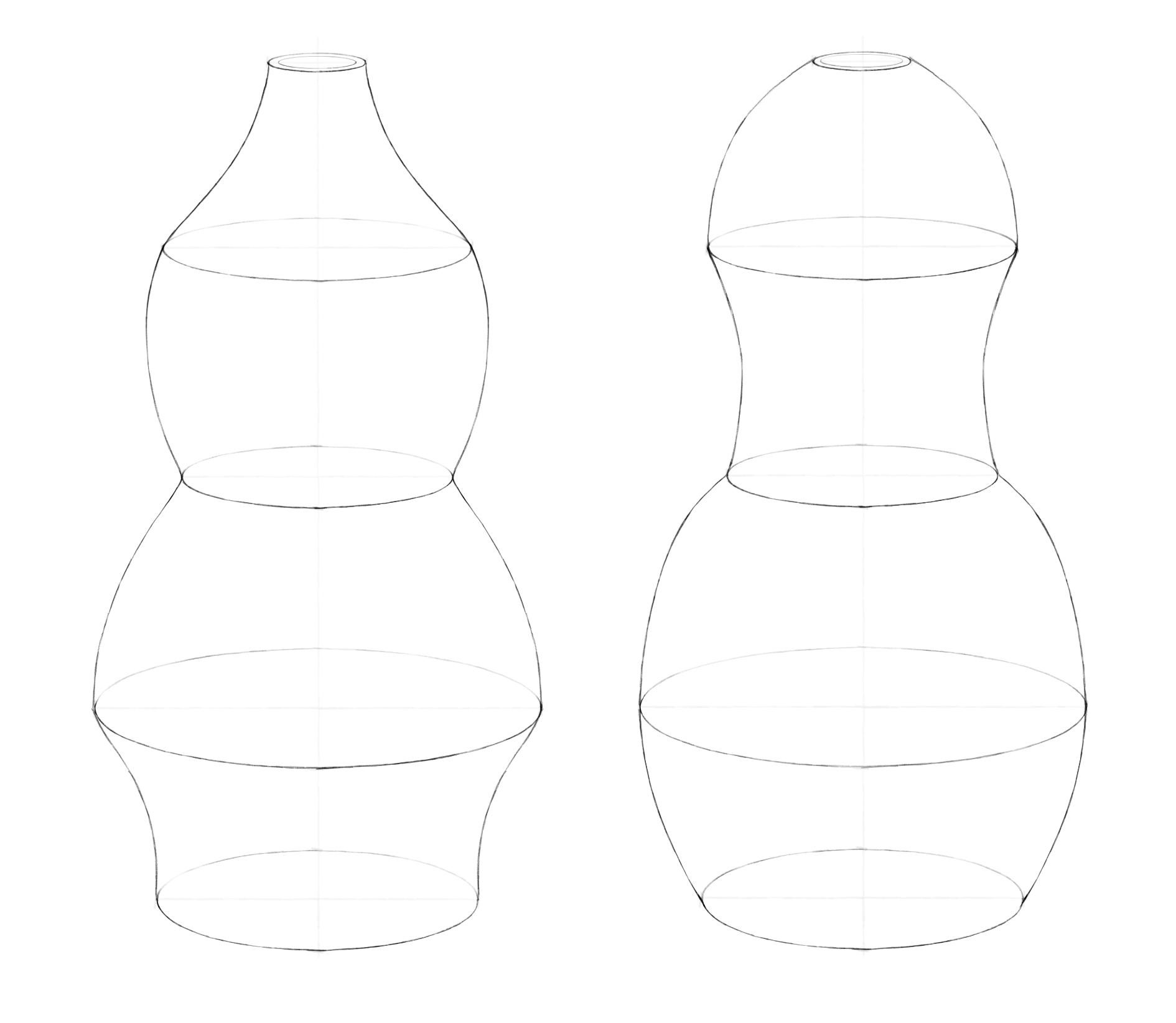
Проверьте свои знания
Читайте также:


