Как сделать круг с помощью линейки
На этой странице собраны лучшие ролики о том Как нарисовать круг с помощью линейки. Если вы хотите научиться рисовать с нуля, просто начните делать это ежедневно. Постарайтесь понять, в каком направлении искусства вы хотите развиваться: иллюстрации, концепт-арт, графический дизайн, детские рисунки, анимация или что-то другое.
Если вы еще не знаете, то наш сайт поможет вам определиться. Просто просматривайте страницы и пробуйте рисовать то что показано в видеоуроках. Если у вас есть какие-то полезные советы о том Как нарисовать круг с помощью линейки, пожалуйста напишите об этом в комментариях. Тем самым вы поможете и нам и многим другим людям.
После получения базовых навыков вы можете перейти к изучению перспективы, композиции, цвету и освещению. Хороший художник знает все эти аспекты, но вам нужно с чего-то начать.
Помните, рисование - это не талант, это выученный навык и тысячи часов практики.
Для чего он нужен, этот расчет радиуса? Чтобы начертить окружность, нам надо знать радиус этой сомой окружности – то есть расстояние от одной ножки циркуля до другой.
Допустим нам надо нарисовать окружность донышка панамки, и все что мы знаем, это обхват головы ребеночка. Как широко надо раздвинуть ножки циркуля, чтобы в итоге получить окружность, совпадающую с размерами головы ребеночка?
Или нам нужно начертить окружность юбки-солнца, зная только то, что длина окружности должна идеально совпадать с обхватом нашей талии.
Сейчас, чтобы все было предельно ясно и понятно, разберем 2 конкретных случая, которые чаще всего встречаются в работе швей.
Это расчет радиуса донышка панамки. И расчет радиуса на выкройке юбки-солнца.
Ситуация первая – нужно рассчитать радиус и начертить окружность дня панамки для девочки.
Эту история я красиво расписала в картинках прямо с текстом -рассуждением. Чтобы была понятна вся последовательность работы мозга. )))



Значит, чтобы узнать радиус – нам надо наш обхват головы ребеночка поделить на 6,28.
Берем мобильный телефон, находим в нем калькулятор и делим наши 42 см обхвата головы на 6,28 – получаем 6,68 см = то есть 6 см и 6 мм. Это и есть радиус.
Значит, нам надо раздвинуть ножки циркуля на расстояние 6 см 6 мм. И тогда нарисованная нами окружность будет равна 42 см – то есть ляжет ровненько по головке ребенка (только не забудьте ее обвесит отступив на 1 см для припусков на швы).
Ситуация вторая – нужно начертить окружность юбки-солнца. Все что мы знаем это обхват талии и длина юбки которую мы в итоге хотим получить.
В чертеже юбки солнца есть 2 окружности. Маленькая (внутренняя) должна лечь ровненько на нашу талию. То есть длина этой окружности должна совпасть с обхватом талии. Обхват талии 70 см, значит, и длина окружности должна быть 70 см (ну, разве что, там всякие сантиметры туда-сюда в виде припуска на швы, или еще какую дополнительную отделку в виде поясочка или кокеточки)
Значит нам нужно узнать, какого радиуса чертить круг, чтобы окружность в результате получилась длиной в эти нужные нам70 см.
На картинке ниже я все расписала и как рассчитать радиус маленькой окружности и как потом узнать радиус большой окружности.

И когда начерчена маленькая окружность. Все что нам нужно, это к маленькому радиусу прибавить желаемую длину юбки – и мы получаем большой радиус для большой окружности края юбки.

Вот с расчетами мы разобрались. Будем шить юбки и панамки – буду отправлять вас в эту статью.
Теперь давайте разберемся, как нарисовать окружность любого размера без циркуля.
КАК НАРИСОВАТЬ ОКРУЖНОСТЬ БЕЗ ЦИРКУЛЯ.
Вот здесь ниже я проиллюстрировала тремя картинками три способа. Надеюсь что все понятно нарисовано и прописано.

Да это быстрый способ – но надо следить за тем, чтобы карандаши не откланялись в сторону. Угол наклона карандаша изменяем радиус. Или надо чтобы один человек ровно держал один карандаш, а другой ровно перпендикулярно чертил вторым карандашом.
Вообще-то, чем ниже привязана нитка тем точнее будет окружность. Поэтому некоторые пользуются маленькими булавочками. Погрешность при отклонении булавки в сторону небольшая, и при шитье ею можно принебречь.

И все-таки самый вернейший способ начертить точный круг без циркуля, это при помощи обычной линейки и карандаша. Вот как это выглядит:

И далее по кругу, двигаем сантиметр (как часовую стрелку в часах) и отмечаем точки на одном и том же расстоянии – то есть на одной и той же цифре сантиметровой ленты. Вместо ленты можно использовать бечевочку с нанесенной на ней отметкой – главное убедитесь что бечевочка нисколько не тянется.

Ну вот и все – еще один пробел в знаниях устранен – теперь можно и на юбку-солнце замахнуться и на панамку – рассчитывать радиусы мы умеем .
Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами.
Прямая СD, соединяющая две точки на окружности, называется хордой.
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.
Часть круга, ограниченная хордой СD и дугой, называется сигментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.
Угол, образованный двумя радиусами КОА, называется центральным углом.
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
Деление окружности на 4 и 8 одинаковых частей

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.
Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки "а" в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке "b". Радиусом R3 из точки "1" проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние "b-О" даёт сторону правильного десятиугольника.
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки "1" окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.
Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Для деления окружности на любое число равных частей часто пользуются приведённой в статье таблицей коэффициентов для длин хорд заданной окружности.

Формулы для расчёта площадей двумерных геометрических фигур. Площадь треугольника, квадрата, параллелограмма, ромба, трапеции, правильного многоугольника.
Грубейшая ошибка в обозначении центра окружности. В центре обязательно пересечение длинных штрихов, а не коротких(точек).
Грубейшая ошибка в обозначении центра окружности. В центре обязательно пересечение длинных штрихов, а не коротких(точек).

Хоть деление круга на несколько равных частей входит в школьную программу, но со временем основы забываются. А строителям, сантехникам, жестянщикам и другим представителям рабочих специальностей эти знания необходимы. Рассмотрим, как разделить круг на 3, 6 и 12 частей.
Диаметр круга не имеет значения. Если нужен очень большой размер – вместо циркуля используют веревку и карандаш.
Чертим произвольный круг.

Радиус окружности делит ее на 6 равных частей. Поэтому выбираем любую позицию на периметре круга, устанавливаем острие циркуля и находим с двух сторон от нее точки, расстояние до которых равно радиусу.

Затем грифель оставляем на одной из этих точек, а острие перемещаем на такую же длину.

С этой позиции определяем следующую точку.

На окружности получится 3 засечки.

Соединяем засечки с центральной точкой фигуры.

Каждая из трех частей имеет внутренний угол 120°.
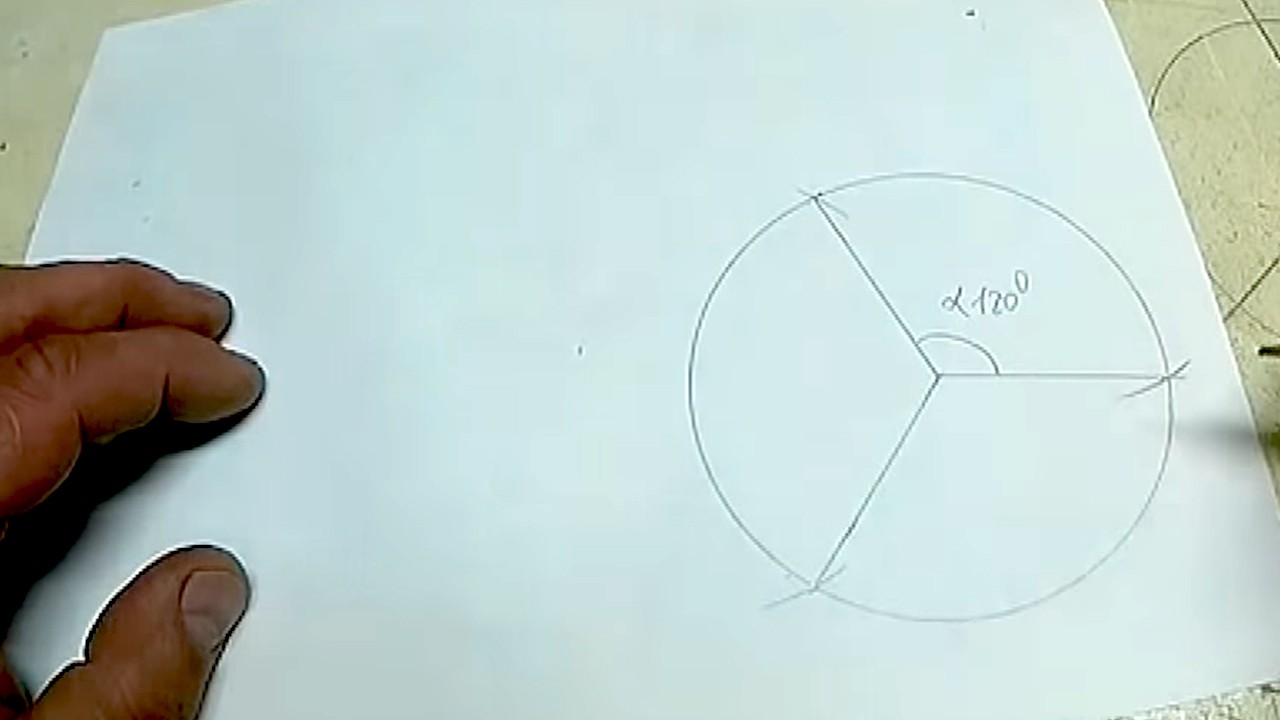
Для деления на 6 частей делаем засечки на окружности, не через одну позицию, а последовательно.

Получаем 6 точек на окружности.
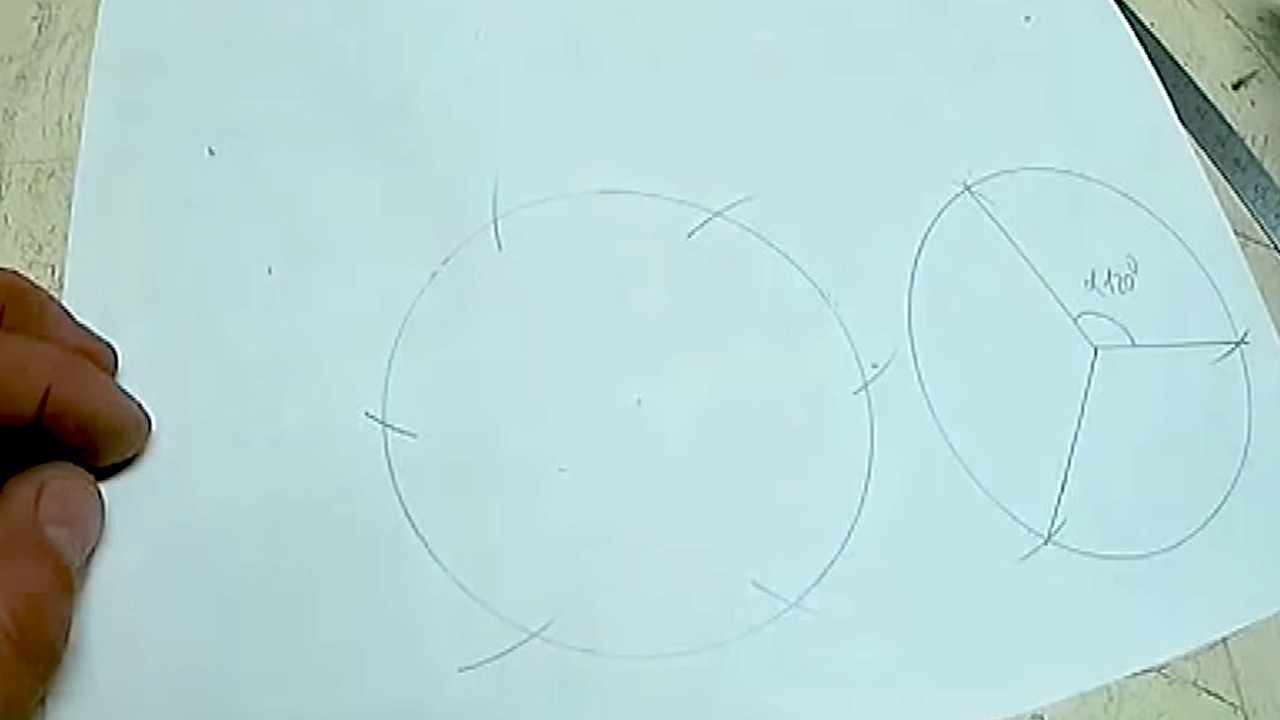
Соединяем точки с центром и параллельной засечкой и получаем 6 частей.


Чтобы разбить на 12 есть, как минимум, 2 способа. Первый способ – расчеты проводятся из круга, деленного на 6 частей.
Для этого из двух ближайших точек окружности проводим 2 дуги за пределы фигуры, навстречу друг другу.
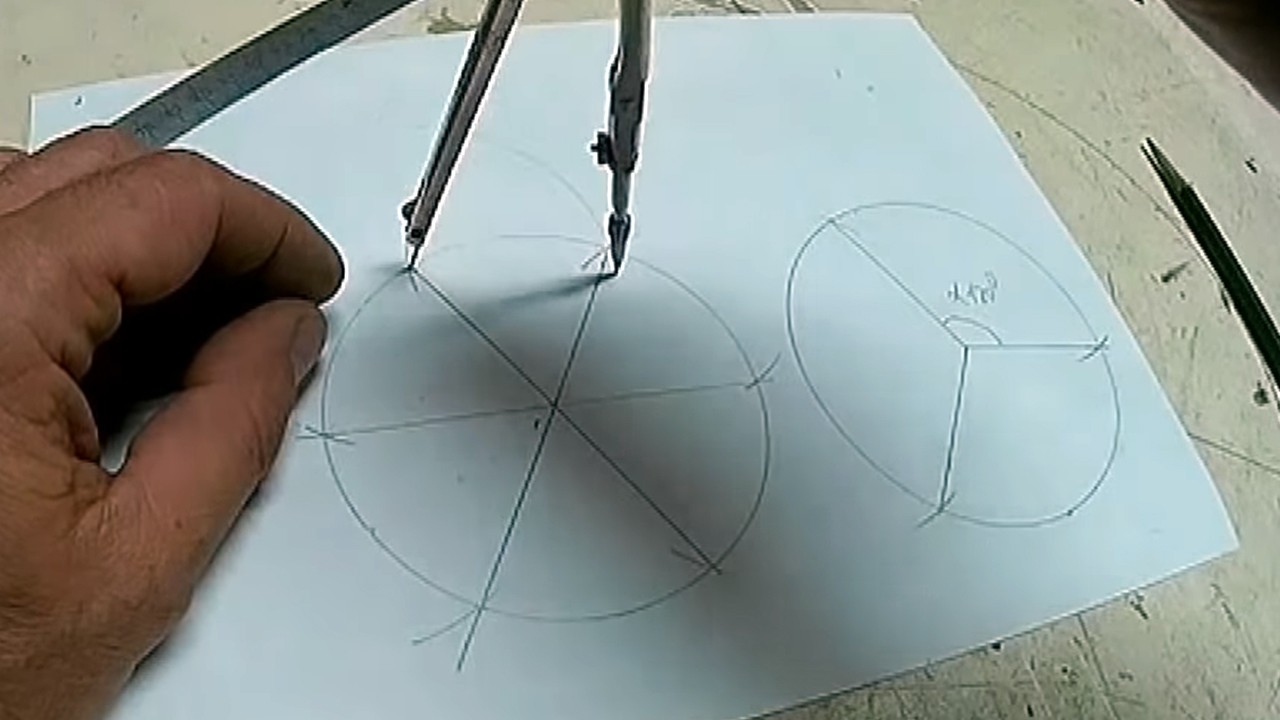
Точку пересечения дуг соединяем с центральной точкой окружности.

Так мы делим 1/6 на 2 части.
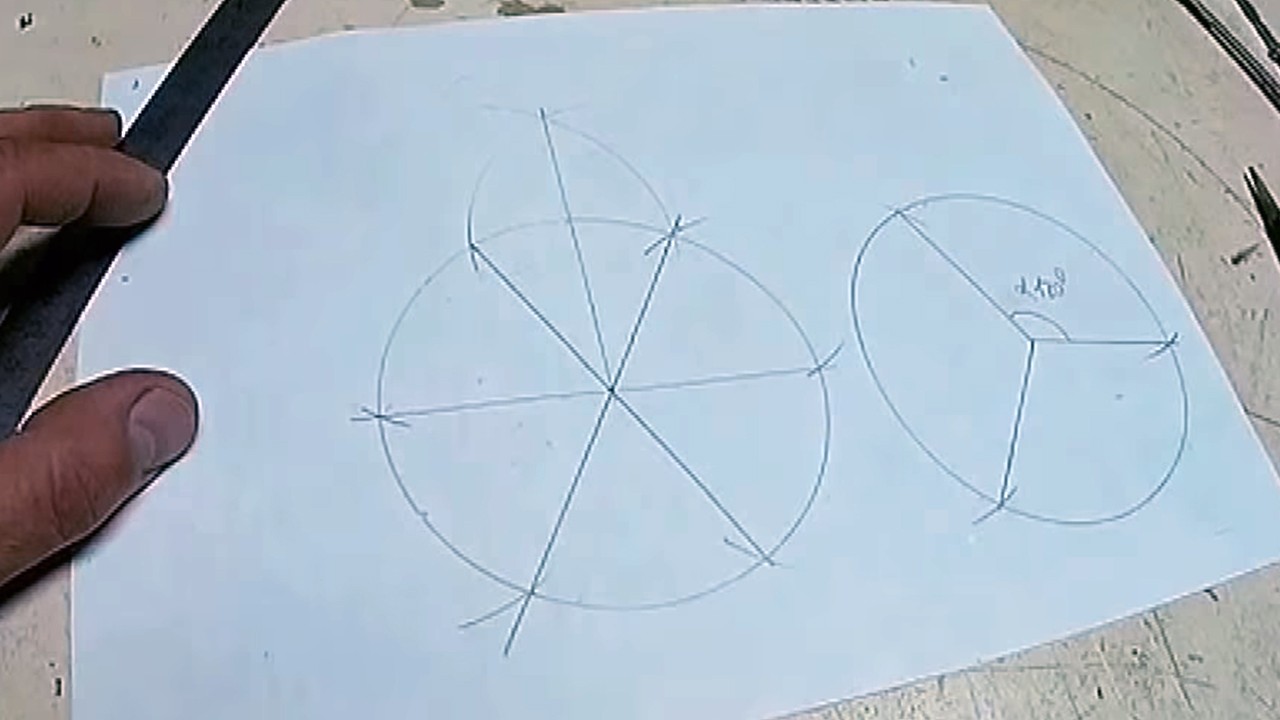
Циркулем измеряем длину получившегося сегмента.

Эту длину откладываем на других частях.

Затем новые засечки соединяем прямыми с центром, получаем деление на 12 частей.

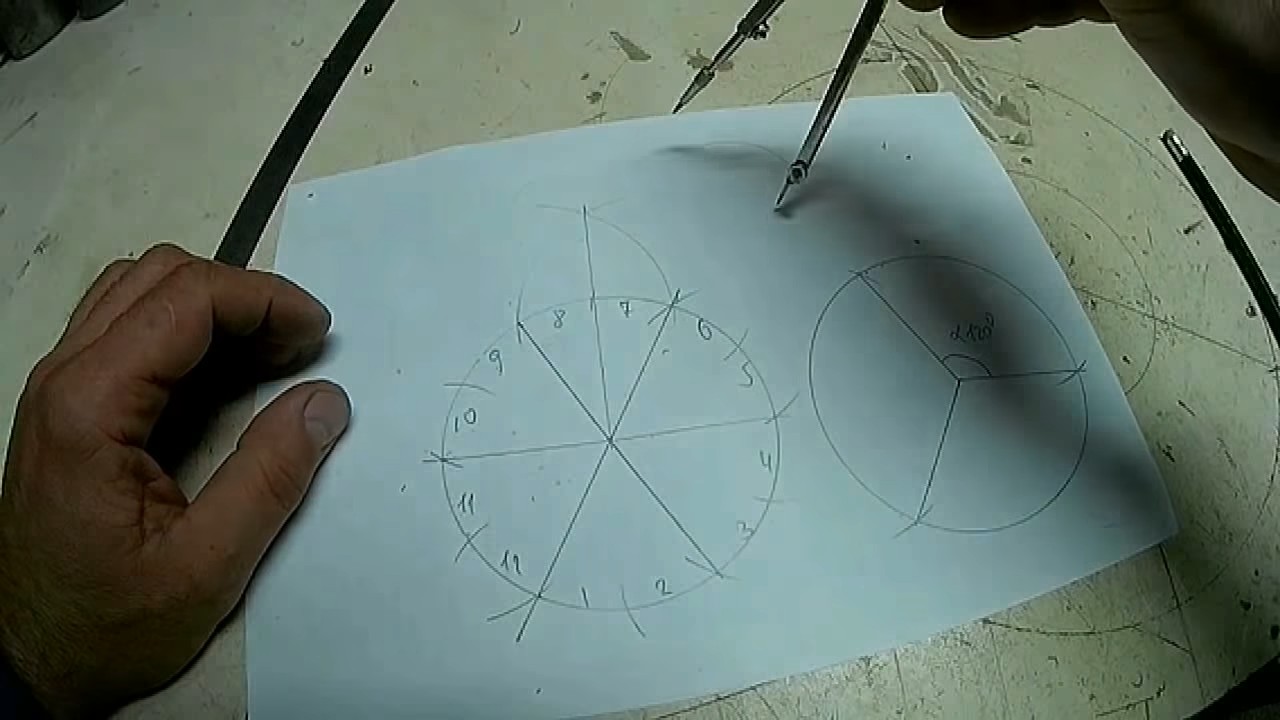
Второй способ – рисуем 2 перпендикулярные прямые через центр окружности, тем самым делим ее на 4 сегмента.

От каждой точки пересечения прямой и окружности в 2 стороны отмеряем расстояние, равное радиусу, намечаем. Так мы получаем снова 12 частей.
Читайте также:


