Как сделать круг на чертеже
1.1. Понятие о стандартах ЕСКД. Если бы каждый инженер или чертежник выполнял и оформлял чертежи по-своему, не соблюдая единых правил, то такие чертежи были бы не понятны другим. Чтобы избежать этого, в СССР приняты и действуют государственные стандарты Единой системы конструкторской документации (ЕСКД).
Стандарты ЕСКД — это нормативные документы, которые устанавливают единые правила выполнения и оформления конструкторских документов во всех отраслях промышленности. К конструкторским документам относят чертежи деталей, сборочные чертежи, схемы, некоторые текстовые документы и пр.
Стандарты установлены не только на конструкторские документы, но и на отдельные виды продукции, выпускаемой нашими предприятиями. Государственные стандарты (ГОСТ) обязательны для всех предприятий и отдельных лиц.
Каждому стандарту присваивается свой номер с одновременным указанием года его регистрации.
Стандарты время от времени пересматривают. Изменения стандартов связаны с развитием промышленности и совершенствованием инженерной графики.
1.2. Форматы. Основная надпись чертежа. Чертежи и другие конструкторские документы промышленности и строительства выполняют на листах определенных размеров.
Для экономного расходования бумаги, удобства хранения чертежей и пользования ими стандарт устанавливает определенные форматы листов, которые обводят тонкой линией. В школе вы будете пользоваться форматом, размеры сторон которого 297X210 мм. Его обозначают А4.
Каждый чертеж должен иметь рамку, которая ограничивает его поле (рис. 18). Линии рамки — сплошные толстые основные. Их проводят сверху, справа и снизу на расстоянии 5 мм от внешней рамки, выполняемой сплошной тонкой линией, по которой обрезают листы. С левой стороны — на расстоянии 20 мм от нее. Эту полоску оставляют для подшивки чертежей.
Рис. 18. Оформление листа формата А4
На чертежах в правом нижнем углу располагают основную надпись (см. рис. 18). Форму, размеры и содержание ее устанавливает стандарт. На учебных школьных чертежах вы будете выполнять основную надпись в виде прямоугольника со сторонами 22X145 мм (рис. 19, а). Образец заполненной основной надписи показан на рисунке 19, б.
Рис. 19. Основная надпись учебного чертежа
Производственные чертежи, выполняемые на листах формата А4, располагают только вертикально, а основную надпись на них — только вдоль короткой стороны. На чертежах других форматов основную надпись можно располагать и вдоль длинной, и вдоль короткой стороны.
В виде исключения на учебных чертежах формата А4 основную надпись разрешено располагать как вдоль длинной, так и вдоль короткой стороны листа.
Прежде чем начинать выполнение чертежа, лист прикладывают к чертежной доске. Для этого прикрепляют его одной кнопкой, например, в левом верхнем углу. Затем на доску кладут рейсшину и располагают верхний край листа параллельно ее кромке, как показано на рисунке 20. Прижав лист бумаги к доске, прикрепляют его кнопками сначала в правом нижнем углу, а затем в остальных углах.
Рис. 20. Подготовка листа к работе
Рамку и графы основной надписи выполняют сплошной толстой линией.
-
Какие размеры имеет лист формата А4? На каком расстоянии от внешней рамки надо проводить линии рамки чертежа? Где помещают основную надпись на чертеже? Назовите ее размеры. Рассмотрите рисунок 19 и перечислите, какие сведения в ней указывают.
1.3. Линии. При выполнении чертежей применяют линии различной толщины и начертания. Каждая из них имеет свое назначение.
Рис. 21. Линии чертежа
На рисунке 21 дано изображение детали, называемой валиком. Как видите, чертеж детали содержит разные линии. Для того чтобы изображение было всем понятно, государственный стандарт устанавливает начертание линий и указывает их основное назначение для всех чертежей промышленности и строительства. На уроках технического и обслуживающего труда вы уже применяли различные линии. Вспомним их.
- Сплошная толстая основная линия. Такую линию применяют для изображения видимых контуров предметов, рамки и граф основной надписи чертежа. Ее толщину (s) выбирают в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображений, от формата чертежа.
- Штриховая линия. Она применяется для изображения невидимых контуров предмета. На чертеже, приведенном на рисунке 21, а, штриховой линией показано неглубокое, невидимое на изображении отверстие, имеющее форму цилиндра.
Штриховая линия состоит из отдельных штрихов (черточек) приблизительно одинаковой длины. Длину каждого штриха выбирают от 2 до 8 мм в зависимости от величины изображения. Расстояние между штрихами в линии должно быть от 1 до 2 мм, но приблизительно одинаковое на всем чертеже. Толщина штриховой линии берется от s/3 до s/2.
Штрихпунктирную тонкую линию используют и для указания осей вращения (как на рис. 21), центра дуг окружностей (центровые линии, рис. 22). При этом положение центра должно определяться пересечением штрихов, как на рисунке 22, а, а не точкой, как на рисунке 22, б.
Рис. 22. Проведение центровых линий: а —правильно; б - неправильно, концы осевых центровых линий должны выступать за контуры изображения предмета, но не более чем на 5 мм.
Она используется для проведения выносных и размерных линий (чертеж, приведенный на рисунке 21, содержит не все необходимые размеры).
Рассмотрите рисунок 8 (в начале учебника). Такими линиями показаны места, по которым надо согнуть материал для приведенного на рисунке изделия.
В заключение следует отметить, что толщина линий одного и того же типа должна быть одинакова для всех изображений на данном чертеже.
Сведения о линиях чертежа даны на первом форзаце.
- Каково назначение сплошной толстой основной линии?
- Какая линия называется штриховой? Где она используется? Какова толщина этой линии?
- Где используется на чертеже штрихпунктирная тонкая линия? Какова ее толщина?
- В каких случаях на чертеже используют сплошную тонкую линию? Какой толщины она должна быть?
- Какой линией показывают на развертке линию сгиба?
На рисунке 23 вы видите изображение детали. На нем цифрами 1,2 и т. д. отмечены различные линии. Составьте в рабочей тетради таблицу по данному образцу и заполните ее.
Рис. 23. Задание для упражнений
ПРИМЕР № 1
Линии чертежа
Приготовьте лист чертежной бумаги формата А4. Вычертите рамку и графы основной надписи по размерам, указанным на рисунке 19. Проведите различные линии, как показано на рисунке 24. Можно выбрать и другое расположение групп линий на листе.
Рис. 24. пример № 1
Основную надпись можно расположить как вдоль короткой, так и вдоль длинной стороны листа.
1.4. Шрифты чертежные. Размеры букв и цифр чертежного шрифта. Все надписи на чертежах должны быть выполнены чертежным шрифтом (рис. 25). Начертание букв и цифр чертежного шрифта устанавливается стандартом. Стандарт определяет высоту и ширину букв и цифр, толщину линий обводки, расстояние между буквами, словами и строчками.
Рис. 25. Надписи на чертежах
Пример построения одной из букв во вспомогательной сетке показан на рисунке 26.
Рис. 26. Пример построения буквы
Шрифт может быть как с наклоном (около 75°), так и без наклона.
Стандарт устанавливает следующие размеры шрифта: 1,8 (не рекомендуется, но допускается); 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. За размер (h) шрифта принимается величина, определяемая высотой прописных (заглавных) букв в миллиметрах. Высота буквы измеряется перпендикулярно к основанию строки. Нижние элементы букв Д, Ц, Щ и верхний элемент буквы Й выполняют за счет промежутков между строками.
Толщину (d) линии шрифта определяют в зависимости от высоты шрифта. Она равна 0,1h;. Ширину (g) буквы выбирают равной 0,6h или 6d. Ширина букв А, Д, Ж, М, Ф, X, Ц, Щ, Ш, Ъ, Ы, Ю больше этой величины на 1 или 2d (включая нижние и верхние элементы), а ширина букв Г, 3, С меньше на d.
Высота строчных букв примерно соответствует высоте следующего меньшего размера шрифта. Так, высота строчных букв размера 10 равна 7, размера 7 равна 5 и т. д. Верхние и нижние элементы строчных букв выполняются за счет расстояний между строками и выходят за строку на 3d. Ширина большинства строчных букв равна 5d. Ширина букв а, м, ц, ъ равна 6d, букв ж, т, ф, ш, щ, ы, ю - 7d, а букв з, с — 4d.
Расстояние между буквами и цифрами в словах принимают равным 0,2h или 2d, между словами и числами —0,6h или 6d. Расстояние между нижними линейками строк берут равным 1,7h или 17d.
Стандарт устанавливает и другой тип шрифта — тип А, более узкий, чем только что рассмотренный.
Высота букв и цифр на чертежах, выполненных в карандаше, должна быть не менее 3,5 мм.
Начертание латинского алфавита по ГОСТу показано на рисунке 27.
Рис. 27. Латинский шрифт
Как писать чертежным шрифтом. Оформлять чертежи надписями надо аккуратно. Нечетко сделанные надписи или небрежно нанесенные цифры разных чисел могут быть неправильно поняты при чтении чертежа.
Чтобы научиться красиво писать чертежным шрифтом, вначале для каждой буквы чертят сетку (рис. 28). После овладения навыками написания букв и цифр можно проводить только верхнюю и нижнюю линии строки.
Рис. 28. Примеры выполнения надписей чертежным шрифтом
Контуры букв намечают тонкими линиями. Убедившись, что буквы написаны правильно, обводят их мягким карандашом.
Для букв Г, Д, И, Я, Л, М, П, Т, X, Ц, Ш, Щ можно провести только две вспомогательные линии на расстоянии, равном их высоте А.
Для букв Б, В, Е, Н. Р, У, Ч, Ъ, Ы, Ь. Я между двумя горизонтальными линиями следует добавить посредине еще одну, но которой выполняют средние их элементы. А для букв 3, О, Ф, Ю проводят четыре линии, где средние линии указывают границы скруглений.
Для быстрого выполнения надписей чертежным шрифтом иногда пользуются различными трафаретами. Основную надпись вы будете заполнять шрифтом 3,5, название чертежа — шрифтом 7 или 5.
1.5. Как наносят размеры. Для определения величины изображенного изделия или какой-либо его части но чертежу на нем наносят размеры. Размеры разделяют на линейные и угловые. Линейные размеры характеризуют длину, ширину, толщину, высоту, диаметр или радиус измеряемой части изделия. Угловой размер характеризует величину угла.
Линейные размеры на чертежах указывают в миллиметрах, но обозначение единицы измерения не наносят. Угловые размеры указывают в градусах, минутах и секундах с обозначением единицы измерения.
Общее количество размеров на чертеже должно быть наименьшим, но достаточным для изготовления и контроля изделия.
Правила нанесения размеров установлены стандартом. Некоторые из них вы уже знаете. Напомним их.
1. Размеры на чертежах указывают размерными числами и размерными линиями. Для этого сначала проводят выносные линии перпендикулярно отрезку, размер которого указывают (рис. 29, а). Затем на расстоянии не менее 10 мм от контура детали проводят параллельную ему размерную линию. Размерная линия ограничивается с двух сторон стрелками. Какой должна быть стрелка, показано на рисунке 29, б. Выносные линии выходят за концы стрелок размерной линии на 1. 5 мм. Выносные и размерные линии проводят сплошной тонкой линией. Над размерной линией, ближе к ее середине, наносят размерное число.
Рис. 29. Нанесение линейных размеров
2. Если на чертеже несколько размерных линий, параллельных друг другу, то ближе к изображению наносят меньший размер. Так, на рисунке 29, в сначала нанесен размер 5, а затем 26, чтобы выносные и размерные линии на чертеже не пересекались. Расстояние между параллельными размерными линиями должно быть не менее 7 мм.
3. Для обозначения диаметра перед размерным числом наносят специальный знак — кружок, перечеркнутый линией (рис. 30). Если размерное число внутри окружности не помещается, его выносят за пределы окружности, как показано на рисунке 30, в и г. Аналогично поступают при нанесении размера прямолинейного отрезка (см. рис. 29, в).
Рис. 30. Нанесение размера окружностей
4. Для обозначения радиуса перед размерным числом пишут прописную латинскую букву R (рис. 31, а). Размерную линию для указания радиуса проводят, как правило, из центра дуги и оканчивают стрелкой с одной стороны, упирающейся в точку дуги окружности.
Рис. 31. Нанесение размеров дуг и угла
5. При указании размера угла размерную линию проводят в виде дуги окружности с центром в вершине угла (рис. 31, б).
6. Перед размерным числом, указывающим сторону квадратного элемента, наносят знак "квадрата" (рис. 32). При этом высота знака равна высоте цифр.
Рис. 32. Нанесение размера квадрата
7. Если размерная линия расположена вертикально или наклонно, то размерные числа располагают, как показано на рисунках 29, в; 30; 31.
9. При изображении плоских деталей в одной проекции толщина детали указывается, как показано на рисунке 29, в. Обратите внимание, что перед размерным числом, указывающим толщину детали, стоит латинская строчная буква 5.
10. Допускается подобным образом указывать и длину детали (рис. 33), но перед размерным числом в этом случае пишут латинскую букву l.
Рис. 33. Нанесение размера длины детали
- В каких единицах выражают линейные размеры на машиностроительных чертежах?
- Какой толщины должны быть выносные и размерные линии?
- Какое расстояние оставляют между контуром изображения и размерными линиями? между размерными линиями?
- Как наносят размерные числа на наклонных размерных линиях?
- Какие знаки и буквы наносят перед размерным числом при указании величины диаметров и радиусов?
Рис. 34. Задание для упражнений
- Перечертите в рабочую тетрадь, сохраняя пропорции, изображение детали, данное на рисунке 34, увеличив его в 2 раза. Нанесите необходимые размеры, укажите толщину детали (она равна 4 мм).
- Начертите в рабочей тетради окружности, диаметры которых равны 40, 30, 20 и 10 мм. Нанесите их размеры. Начертите дуги окружности с радиусами 40, 30, 20 и 10 мм и нанесите размеры.
1.6. Масштабы. В практике приходится выполнять изображения очень крупных деталей, например деталей самолета, корабля, автомашины, и очень мелких — деталей часового механизма, некоторых приборов и др. Изображения крупных деталей могут не поместиться на листах стандартного формата. Мелкие детали, которые еле заметны невооруженным глазом, невозможно вычертить в натуральную величину имеющимися чертежными инструментами. Поэтому при вычерчивании больших деталей их изображение уменьшают, а малых увеличивают по сравнению с действительными размерами.
Масштаб — это отношение линейных размеров изображения предмета к действительным. Масштабы изображений и их обозначение на чертежах устанавливает стандарт.
Масштаб уменьшения—1:2; 1:2,5; 1:4; 1:5; 1:10 и др.
Натуральная величина—1:1.
Масштаб увеличения—2:1; 2,5:1; 4:1; 5:1; 10:1 и др.
Наиболее желателен масштаб 1:1. В этом случае при выполнении изображения не нужно пересчитывать размеры.
Масштабы записывают так: M1:1; M1:2; M5:1 и т. д. Если масштаб указывают на чертеже в специально предназначенной для этого графе основной надписи, то перед обозначением масштаба букву М не пишут.
Следует помнить, что, в каком бы масштабе ни выполнялось изображение, размеры на чертеже наносят действительные, т. е. те, которые должна иметь деталь в натуре (рис. 35).
Угловые размеры при уменьшении или увеличении изображения не изменяются.
- Для чего служит масштаб?
- Что называется масштабом?
- Какие вам известны масштабы увеличения, установленные стандартом? Какие вам известны масштабы уменьшения?
- Что означают записи: М1:5; М1:1; М10:1?
Рис. 35. Чертеж прокладки, выполненный в различных масштабах
Работу выполните на листе формата А4. Масштаб изображения 2:1.
Указания к работе. На рисунке 36 дана лишь половина изображения детали. Вам нужно представить, как будет выглядеть деталь полностью, помня о симметрии, выполнить эскизно ее изображение на отдельном листе. Затем следует перейти к выполнению чертежа.
На листе формата А4 чертят рамку и выделяют место для основной надписи (22Х145 мм). Определяют центр рабочего поля чертежа и от него ведут построение изображения.
Вначале проводят оси симметрии, строят тонкими линиями прямоугольник, соответствующий общей форме детали. После этого размечают изображения прямоугольных элементов детали.
Рис. 36. пример № 2
Определив положение центров окружности и полуокружности, проводят их. Наносят размеры элементов и габаритные, т. е. наибольшие по длине и высоте, размеры детали, указывают ее толщину.
Обводят чертеж линиями, установленными стандартом: сначала — окружности, затем — горизонтальные и вертикальные прямые. Заполняют основную надпись и проверяют чертеж.
При разметке все построения производятся с помощью двух линий — прямой и окружности (на рис. 3.42 с целью повторения представлены элементы окружности).

Рис. 3.42. Окружность и ее элементы
Нахождение центра окружности. На плоских деталях, где уже имеются готовые отверстия, центр которых неизвестен, его находят геометрическим способом. На торцах цилиндрических деталей нахождение центра производят при помощи циркуля, рейсмуса, угольника-цетроискателя и колокола.
Разметка центра по угольнику-центроискателю. Разметку выполняют в следующей последовательности.
- 1. Деталь устанавливают на разметочную плиту так, чтобы размечаемый торец был сверху.
- 2. На торец цилиндрической детали накладывают угольник-центроиска- тель так, чтобы две его стороны (планки) касались цилиндрической поверхности детали, рис. 3.43.

Рис. 3.43. Нахождение центра окружности с помощью угольника-центроискателя
- 3. Левой рукой плотно прижимают линейку угольника к поверхности торца, а правой проводят чертилкой первую диаметральную риску.
- 4. Угольник-центроискатель поворачивают по цилиндрической поверхности детали примерно на 90° и проводят вторую риску. Точка пересечения двух рисок будет центром размечаемой окружности.
Разметку центра детали с грубо обработанной цилиндрической поверхностью производят в такой же последовательности. В этом случае для более точного нахождения центра окружности необходимо нанести пять-семь рисок. Центром будет точка, в которой пересекается наибольшее число рисок.
Точность разметки центра окружности проверяют разметочным циркулем, рис. 3.44. Острие одной ножки циркуля устанавливают в размеченный центр, а другую ножку перемещают так, чтобы ее острие слегка касалось цилиндрической части детали. Если острие ножки циркуля касается по всей длине окружности, то центр размечен правильно.

Рис. 3.44. Способ проверки точности разметки центра окружности разметочным циркулем
Разметка центра рейсмусом (рис. 3.45). Деталь кладут на призмы или параллельные подкладки, уложенные на разметочную плиту. Устанавливают острый конец иглы рейсмуса несколько выше или ниже центра размечаемой

Рис. 3.45. Разметка центра рейсмусом
детали и, придерживая деталь левой рукой, правой рукой движением рейсмуса по плите прочерчивают его иглой на торце детали короткую рису. После этого поворачивают деталь на 1/4 окружности и таким же способом проводят вторую риску. То же повторяют через каждую четверть оборота для проведения третьей и четвертой рисок. Внутри рисок (на пересечении диагоналей) и будет находиться центр. Его набивают кернером.
Геометрический способ нахождения центра заключается в следующем. Пусть дана плоская металлическая плита с готовым отверстием, центр которого неизвестен. Перед тем как начать разметку, вставляют в отверстие широкий деревянный брусок и на него набивают пластинку из белой жести или из оцинкованного кровельного железа.
Затем на краю отверстия слегка намечают произвольно три точки Л, В и С и из каждой пары этих точек ЛВ и ВС описывают по обе стороны их пересекающиеся между собой дуги-засечки 1—2 и 3—4, рис. 3.46. Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.

Рис. 3.46. Нахождение центра геометрическим способом
Разметка центра циркулем (кронциркулем). Зажав деталь в тиски, растворяют ножки циркуля на величину, немного большую или немного меньшую радиуса размечаемой детали. После этого, приложив к боковой поверхности детали одну ножку циркуля и придерживая ее большим пальцем, другой ножкой циркуля очерчивают дугу. Далее переместив циркуль на 1/4 окружности (на глаз), таким же образом очерчиваю вторую дугу. Затем через каждую четверть окружности очерчивают третью и четвертую дуги. Затем соединить противоположные засечки диагоналями, рис. 3.47я. Центр окружности будет находиться внутри очерченных дуг на пересечении диагоналей.

Рис. 3.47. Разметка центра циркулем (кронциркулем)
Можно разметить центр и способом, показанным на рис. 3.476. Методика разметки аналогична разметке рейсмусом.
Разметка центра колоколом. Приспособление колокол устанавливается на торец цилиндрической детали. Придерживая колокол левой рукой в вертикальном положении, правой рукой наносят удар молотком по кернеру, находящемуся в колоколе, рис. 3.48. Кернер сделает углубление в центре торца.

Рис. 3.48. Разметка центра колоколом
Деление окружности на равные части. При разметке окружностей часто приходится их делить на несколько равных частей — 3, 4, 5, 6, и больше. Ниже приведены примеры деления окружности на равные части геометрическим способом и с помощью таблиц.
Деление окружности на три равные части с построением вписанного треугольника (рис. 3.49).

Рис. 3.49. Деление окружности на три части с построением вписанного треугольника
- 1. В центре размечаемой плоскости с помощью циркуля проводим окружность требуемого радиуса, например R = 26 мм.
- 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
- 3. Опорную ножку циркуля устанавливаем в точку А и при растворе циркуля, равном радиусу проведенной окружности, делаем на окружности две метки-засечки (точки С и D), где длина дуги между ними будет равна одной трети длины окружности.
- 4. Соединив точки прямыми рисками СД СВ и BD, получим вписанный равносторонний треугольник.
- 5. Правильность построения проверяем циркулем, устанавливая раствор циркуля равным одной из сторон треугольника и этим же размером определяя равенство остальных сторон треугольника.
Деление окружности на четыре равные части с построением вписанного квадрата, рис. 3.50.

Рис. 3.50. Деление окружности на четыре части с построением вписанного квадрата (а) и прием разметки квадрата (6)
- 1. В центре размечаемой плоскости циркулем проводим окружность требуемого радиуса, например R= 28 мм.
- 2. Через центр окружности по линейке проводим прямую риску что бы она пересекала окружности в двух точках А и В и разделяла ее на две равные части.
- 3. Опорную ножку циркуля устанавливаем в точку А и, раздвинув циркуль на расстояние несколько большее, чем половина отрезка АВ, проводим дугу в.
- 4. Опорную ножку циркуля переносим в точку В и, не изменяя раствора циркуля, проводим дугу б так, чтобы она пересекла первую выполненную дугу в точках 7 и 2.
- 5. Через точки 7 и 2 проводим риску, которая образует на окружности точки С и D.
- 6. Соединив точки AD, DB, ВС и СА прямыми рисками, получим квадрат, вписанный в окружность.
Деление окружности на пять равных частей (рис. 3.51). На данной окружности проводим два взаимно перпендикулярных диаметра, пересекающие окружность в точках А и В, С и D. Радиус ОА делим пополам и из полученной точки Е описываем дугу радиусом ЕС до пересечения в точке F на радиусе О В. После этого соединяем прямой точки D и F. Откладывая длину прямой DF по окружности, разделим ее на пять равных частей.
Деление окружности на шесть равных частей с построением вписанного шестиугольника, рис. 3.52.

Рис. 3.51. Деление окружности на пять равных частей

Рис. 3.52. Деление окружности на шесть частей с построением вписанного шестиугольника
- 1. В центре разметочной плоскости циркулем проводим окружность требуемого радиуса, например 7? = 27 мм.
- 2. Через центр окружности по линейке проводим прямую риску с пересечением окружности в точках А и В.
- 3. Из точки А, как из центра, наносим дугу радиусом, равным радиусу проведенной окружности, и получаем точки 7 и 2
Аналогичное построение делаем из точки В, нанося точки 3 и 4. Полученные точки пересечения и концевые точки диаметра будут искомыми точками деления окружности на шесть частей.
4. Соединив точки прямыми рисками А — 1,2 — 4, 4 — В, В — 3, 3 — 1 и 1 — А, получим вписанный шестиугольник.
При разметке граней шестиугольника под размер h зева гаечного ключа (рис. 3.53) радиус описываемой окружности определяется по формуле R = 0,577/г.

Рис. 3.53. Пример разметки шестиугольника под размер зева гаечного ключа
Таблица 3.5. Деление окружности на равные части
Число делений окружности
Число, умножаемое на радиус окружности
Число делений окружности
Число, умножаемое на радиус окружности
Число делений окружности
Число, умножаемое на радиус окружности
Окончание табл. 3.5
Число делений окружности
Число, умножаемое на радиус окружности
Пример 1. Требуется разделить на 15 равных частей окружность, радиус которой равен 280 мм. Сначала определяем величину хорды, т. е. расстояние между двумя соседними делениями. Для этого из второй графы табл. 3.5 берем число, стоящее против цифры 15 первой графы (в данном случае это будет 0,4158), и умножаем на это число радиус окружности.

Это расстояние берем циркулем по масштабной линейке и откладываем его на размечаемой окружности. Последняя разделится на 15 равных частей.
Пример 2. Требуется разделить на 13 равных частей окружность, диаметр которой равен 500 мм.
По таблице число, соответствующее 13 делениям, составляет 0,4786. Следовательно

Отложим циркулем полученное расстояние размечаемой окружности, разделим ее на 13 равных частей.
Разметка отверстий на деталях. Разметка отверстий под болты и шпильки в плоских деталях, кольцах и фланцах для труб и цилиндров машин требует особого внимания. Центры отверстий болтов и шпилек должны быть точно расположены (размечены) по окружности — так, чтобы при наложении двух сопрягаемых деталей соответствующие отверстия приходились строго одно под другим.
После того как размеченная окружность (рис. 3.54) разделена на части и в надлежащих местах по этой окружности накернены центры отверстий, приступают к разметке отверстий. При кернении центров сначала накернивают углубление лишь слегка и затем проверяют циркулем равенство расстояния между центрами. Только убедившись в правильности разметки, накернивают центры окончательно.

Рис. 3.54. Разметка отверстий: 1 — размечаемое кольцо; 2 — деревянная планка, забитая в отверстие; 3 — проведение окружности; 4 — разбивка отверстий; 5 — размеченные отверстия; 6 — окружность центров отверстий; 7 — контрольная окружность; 8 — керны
Отверстия размечают двумя окружностями из одного центра. Первую окружность проводят радиусом по размеру отверстия, а вторую окружность, как контрольную — радиусом на 1,5—2,0 мм большим, чем первый. Это необходимо для того, чтобы при сверлении можно было видеть, не сместился ли центр и правильно ли идет сверление. Первую окружность накернивают — для малых отверстий делают 4 керна, для больших — 6—8 и больше.
На рис. 3.55 приведен пример разметки фланца задвижки.

Рис. 3.55. Пример разметки отверстий на фланце задвижки: а — задвижка и элементы разметки; б — разметка фланца на шесть отверстий; в — разметка под четыре отверстия; г — под восемь отверстий
Круг - это геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга не превышает заданного расстояния, называемого радиусом этого круга.
Чертеж круга выполняется на основании ГОСТ 2.109-73 - единая система конструкторской документации (ЕСКД).

Вы можете бесплатно скачать этот простой чертеж для использования в любых целях. Например для размещения на шильдике или наклейке.
Как начертить чертеж:
Начертить чертеж можно как на листе бумаги, так и с использованием специализированных программ. Для выполнения простых эскизных чертежей особых инженерных знаний не требуется.
Конструкторский чертеж со всеми технологическими данными для изготовления может выполнить только квалифицированный инженер.
Для обозначения на чертеже необходимо выполнить следующие операции:
1. Начертить изображение;
2. Проставить размеры (см пример);
3. Указать технические требования к изготовлению (подробнее о технических требованиях читайте ниже в статье).
Чертить удобнее всего на компьютере. В последующем чертеж можно распечатать на бумаге на принтере или плоттере. Есть множество специализированных программ для черчения на компьютере. Как платных, так и бесплатных.
Пример черчения:
На этом изображении нарисовано как просто и быстро выполняется чертеж с помощью компьютерных программ.

Список программ для черчения на компьютере:
1. КОМПАС-3D;
2. AutoCAD;
3. NanoCAD;
4. FreeCAD;
5. QCAD.
Изучив принципы черчения в одной из программ не сложно перейти на работу в другой программе. Методы черчения в любой программе принципиально не отличаются друг от друга. Можно сказать что они идентичны и отличаются друг от друга только удобством и наличием дополнительных функций.
Технические требования:
Для чертежа необходимо проставить размеры, достаточные для изготовления, предельные отклонения и шероховатость.
В технических требованиях к чертежу следует указать:
1) Способ изготовления и контроля, если они являются единственными, гарантирующими требуемое качество изделия;
2) Указать определенный технологический прием, гарантирующий обеспечение отдельных технических требований к изделию.
Немного теории:
Чертёж - это проекционное изображение изделия или его элемента, один из видов конструкторских документов содержащий данные для производства и эксплуатации изделия.
Чертеж это не рисунок. Чертеж выполняется по размерам и в масштабе реального изделия (конструкции) или части изделия. Поэтому для выполнения чертежных работ необходима работа инженера, обладающего достаточным опытом в производстве чертежных работ (впрочем для красивого отображения изделия для буклетов вполне возможно понадобится услуга художника, обладающего художественным взглядом на изделие или его часть).
Чертеж - это конструктивное изображение с необходимой и достаточной информацией о габаритах, методе изготовления и эксплуатации. Представленный на этой странице чертеж вы можете скачать бесплатно.
Рисунок - это художественное изображение на плоскости, созданное средствами графики (кисть, карандаш или специализированная программа).
Чертеж может быть как самостоятельным документом, так и частью изделия (конструкции) и технических требований, относящиеся к поверхностям, обрабатываемым совместно. Указания о совместной обработке помещают на всех чертежах, участвующих в совместной обработке изделий.
Подробнее о чертежах, технических требованиях к оформлению и указанию методов изготовления смотрите в ГОСТ 2.109-73. Перечень стандартов для разработки конструкторской документации смотрите здесь.
Информация для заказа чертежей:
В нашей проектной организации Вы можете заказать чертеж любого изделия (как детали, так и сборки), в составе которого будет чертеж круга, как элемент конструкторской документации изделия в целом. Наши инженеры-конструкторы разработают документацию в минимальные сроки в точном соответствии с Вашим техническим заданием.

Раздел 3: Чтение и выполнение чертежей (7 часов)
Выполнение чертежей предметов с использованием геометрических построений (деление окружности на равные части, деление углов и отрезков на равные части; сопряжения). Общее понятие о форме и формообразовании предметов. Анализ геометрической формы предметов. Способы чтения и выполнения чертежей на основе анализа формы. Построение третьей проекции предмета по двум заданным. Нахождение на чертеже вершин, ребер и граней, поверхностей геометрических тел, составляющих форму предмета. Определение необходимого и достаточного количества видов на чертеже. Творческие задачи на пройденный материал.
Урок № 11: Деление окружности на равные части

Ботвинников А.Д. § 15.2 [1]
Степакова В. В. § 15 [3]
Вышнепольский И.С. § 8 [8]

При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений.
Деление окружности на равные части с помощью циркуля
Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7, 8, 12 равных участков.
Деление окружности на четыре равные части.
Штрихпунктирные центровые линии, проведенные перпендикулярно одна другой, делят окружность на четыре равные части. Последовательно соединив их концы, получим правильный четырехугольник (рис. 1) .
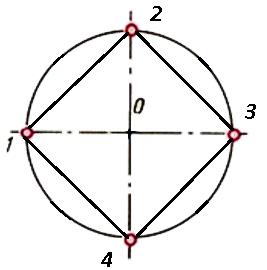
Рис.1 Деление окружности на 4 равные части.
Деление окружности на восемь равных частей.
Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 2).
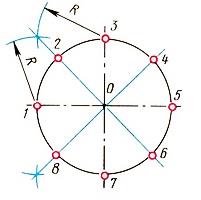
Рис.2. Деление окружности на 8 равных частей.
Деление окружности на шестнадцать равных частей.
Разделив циркулем дугу, равную 1/8, на две равные части, нанесём засечки на окружность. Соединив все засечки, отрезками прямых, получим правильный шестнадцатиугольник.
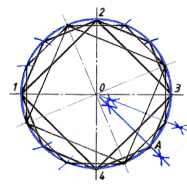
Рис.3. Деление окружности на 16 равных частей.
Деление окружности на три равные части.
Чтобы разделить окружность радиуса R на 3 равные части, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу радиусом R. Получают точки 2 и 3. Точки 1, 2, 3 делят окружность на три равные части.
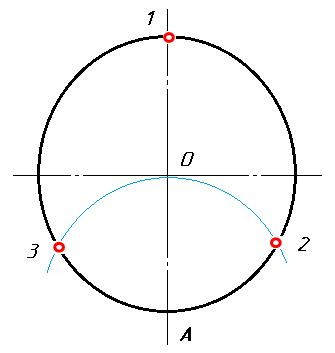
Рис. 4. Деление окружности на 3 равные части.
Деление окружности на шесть равных частей. Сторона правильного шестиугольника, вписанного в окружность, равна радиусу окружности (рис. 5.).
Для деления окружности на шесть равных частей надо из точек 1 и 4 пересечения центровой линии с окружностью сделать на окружности по две засечки радиусом R, равным радиусу окружности. Соединив полученные точки отрезками прямых, получим правильный шестиугольник.
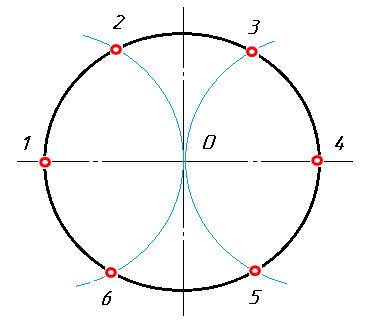
Рис. 5. Деление окружности на 6 равных частей
Деление окружности на двенадцать равных частей.
Чтобы разделить окружность на двенадцать равных частей, надо окружность поделить на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 6).
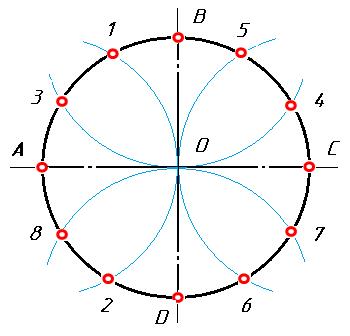
Рис. 6. Деление окружности на 12 равных частей
Деление окружности на пять равных частей
Из точки А проведем дугу тем же радиусом, что и радиус окружности до пересечения с окружностью – получим точку В. Опустив перпендикуляр с этой точки – получим точку С. Из точки С – середины радиуса окружности, как из центра, дугой радиуса СD сделаем засечку на диаметре, получим точку Е. Отрезок DЕ равен длине стороны вписанного правильного пятиугольника. Сделав радиусом DЕ засечки на окружности, получим точки деления окружности на пять равных частей.
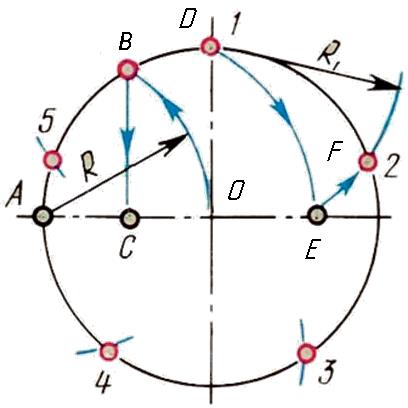
Рис. 7. Деление окружности на 5 равных частей
Деление окружности на десять равных частей
Разделив окружность на пять равных частей, легко можно разделить окружность и на 10 равных частей. Проведя прямые от получившихся точек через центр окружности до противоположных сторон окружности – получим ещё 5 точек.
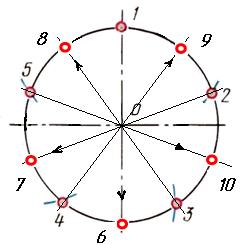
Рис. 8. Деление окружности на 10 равных частей
Деление окружности на семь равных частей
Чтобы разделить окружность радиуса R на 7 равных частей, из точки пересечения центровой линии с окружностью (например, из точки А) описывают как из центра дополнительную дугу этим же радиусом R – получают точку В. Опустив перпендикуляр с точки В – получим точку С. Отрезок ВС равен длине стороны вписанного правильного семиугольника.
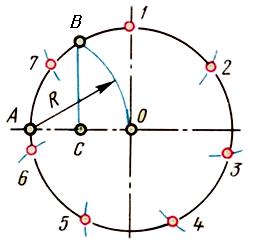
Рис. 9. Деление окружности на 7 равных частей

Практические задания, тесты и домашние работы
Графическая работа

Вопросы для повторения


Домашняя работа
Читайте также:


