Как сделать кривую гаусса в экселе
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.

Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма

Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.

Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.

Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.

Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.

Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Вам также могут быть интересны следующие статьи
13 комментариев
Как построить график с нормальным распределением в Excel
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.

Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма

Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.

Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.

Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.

Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.

Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Вам также могут быть интересны следующие статьи
13 комментариев
Диаграмма нормального распределения (Гаусса) в Excel
Требуется построить диаграмму стандартного нормального распределения Гаусса (стандартное нормальное распределение имеет М = 0 и = 1), используя функцию НОРМСТРАСП.
1. В ячейку A3 введем символ х, а в ячейку ВЗ — символ функции плотности вероятности f(x).
2. Вычислим нижнюю М — За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =0-3*1, а также верхнюю границу — в ячейку Е2 введем формулу =0+3*1.
3. Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.
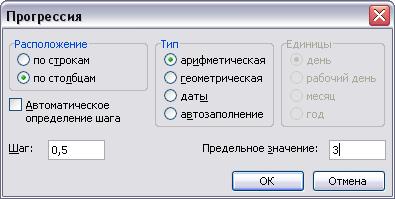
4. Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.
5. В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение — число, равное верхней границе диапазона.
Функция НОРМРАСПР в EXCEL
6. Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.
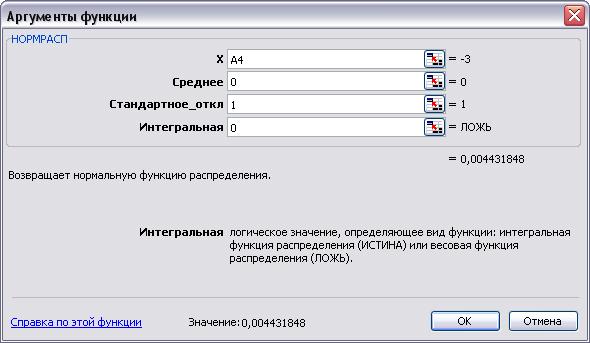
7. Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций — НОРМРАСП.
8. Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее — введем число 0, для параметра Стандартное_откл — число 1, для параметра Интегральное — число 0 (весовая).
Диаграмма нормального интегрального распределения в EXCEL
9. Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В16.
10. Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В16) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид — вид графика, щелкнем на кнопке Далее.
11. В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А16). Щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности .
Как построить распределение гаусса в excel
В этой статье описаны синтаксис формулы и использование ГАУСС в Microsoft Excel.
Описание
Рассчитывает вероятность, с которой элемент стандартной нормальной совокупности находится в интервале между средним и стандартным отклонением z от среднего.
Синтаксис
Аргументы функции ГАУСС указаны ниже.
Z Обязательный. Возвращает число.
Замечания
Поскольку НОРМ.СТ.РАСП(0,Истина) всегда возвращает 0,5, ГАУСС (z) всегда будет на 0,5 меньше, чем НОРМ.СТ.РАСП(z,Истина).
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Вероятность, с которой элемент стандартной нормальной совокупности населения находится в интервале между средним и двумя стандартными отклонениями от среднего (результат — 0,47725).
В связи с написанием диплома тема подсчёта статистики для меня крайне актуальна, посему делюсь найденной крайне полезной стаейкой по построению гистограмм распределения. Точнее частью этой статьи с наипростейшим алгоритмом постороения этих гистограмм Excel. Лично я строю этим способом гистограммы распределения значений показателей психологических тестов, ну а там уж каждому по потребностям, распределение чего надо посмотреть.
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: естественно, в первую очередь я скажу, что металлургии, а также в экономике, биологии, политике, социологии и. много где еще. Статья эта будет, как несложно догадаться по ее названию, про использование некоторых средств статистического анализа, а именно — гистограммам.
Ну, поехали.
А теперь — к построению гистограмм распределения по частоте и их анализу.
Речь пойдет именно о частотных гистограммах, где каждый столбец соответствует частоте появления* значения в пределах границ интервалов. Например, мы хотим посмотреть, как у нас выглядит распределение значения предела текучести стали S355J2 в прокате толщиной 20 мм за несколько месяцев. В общем, хотим посмотреть, похоже ли наше распределение на нормальное (а оно должно быть таким).
*Примечание: для металловедческих целей типа оценки размера зерна или оценки объемной доли частиц этот вид гистограмм не пойдет, т.к. там высота столбика соответствует не частоте появления частиц определенного размера, а доле объема (а в плоскости шлифа — площади), которую эти частицы занимают.
График нормального распределения выглядит следующим образом:

График функции Гаусса
Мы знаем, что реально такой график может быть получен только при бесконечно большом количестве измерений. Реально же для конечного числа измерений строят гистограмму, которая внешне похожа на график нормального распределения и при увеличении количества измерений приближается к графику нормального распределения (распределения Гаусса).
Очень давно не писал блог. Расслабился совсем. Ну ничего, исправляюсь.
Продолжаю новую рубрику блога, посвященную анализу данных с помощью всем известного Microsoft Excel.
В современном мире к статистике проявляется большой интерес, поскольку это отличный инструмент для анализа и принятия решений, а также это отличное средство для поиска причин нарушений процесса и их устранения. Статистический анализ применим во многих сферах, где существуют большие массивы данных: естественно, в первую очередь я скажу, что металлургии, а также в экономике, биологии, политике, социологии и… много где еще. Статья эта будет, как несложно догадаться по ее названию, про использование некоторых средств статистического анализа, а именно — гистограммам.
Ну, поехали.
А теперь — к построению гистограмм распределения по частоте и их анализу.
Речь пойдет именно о частотных гистограммах, где каждый столбец соответствует частоте появления* значения в пределах границ интервалов. Например, мы хотим посмотреть, как у нас выглядит распределение значения предела текучести стали S355J2 в прокате толщиной 20 мм за несколько месяцев. В общем, хотим посмотреть, похоже ли наше распределение на нормальное (а оно должно быть таким).
*Примечание: для металловедческих целей типа оценки размера зерна или оценки объемной доли частиц этот вид гистограмм не пойдет, т.к. там высота столбика соответствует не частоте появления частиц определенного размера, а доле объема (а в плоскости шлифа — площади), которую эти частицы занимают.
График нормального распределения выглядит следующим образом:

График функции Гаусса
Мы знаем, что реально такой график может быть получен только при бесконечно большом количестве измерений. Реально же для конечного числа измерений строят гистограмму, которая внешне похожа на график нормального распределения и при увеличении количества измерений приближается к графику нормального распределения (распределения Гаусса).
А теперь — построение гистограмм!
Способ 1-ый. Халявный.
Способ 2-ой. Трудный, но интересный.
Будет полезен тому, кто по каким-либо причинам не смог установить Пакет анализа.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Для лучшего понимания, вы можете скачать файл с примером построения нормального распределения.
Построим диаграмму распределения в Excel. А также рассмотрим подробнее функции круговых диаграмм, их создание.
Как построить диаграмму распределения в Excel
График нормального распределения имеет форму колокола и симметричен относительно среднего значения. Получить такое графическое изображение можно только при огромном количестве измерений. В Excel для конечного числа измерений принято строить гистограмму.
Внешне столбчатая диаграмма похожа на график нормального распределения. Построим столбчатую диаграмму распределения осадков в Excel и рассмотрим 2 способа ее построения.
Имеются следующие данные о количестве выпавших осадков:
После нажатия ОК получаем такой график с таблицей:
В интервалах не очень много значений, поэтому столбики гистограммы получились низкими.
Теперь необходимо сделать так, чтобы по вертикальной оси отображались относительные частоты.
Способ второй. Вернемся к таблице с исходными данными. Вычислим интервалы карманов. Сначала найдем максимальное значение в диапазоне температур и минимальное.
Представим интервалы карманов в виде столбца значений. Сначала ширину кармана прибавляем к минимальному значению массива данных. В следующей ячейке – к полученной сумме. И так далее, пока не дойдем до максимального значения.
Для определения частоты делаем столбец рядом с интервалами карманов. Вводим функцию массива:
Вычислим относительные частоты (как в предыдущем способе).
Частота распределения заданных значений:
Круговые диаграммы для иллюстрации распределения
С помощью круговой диаграммы можно иллюстрировать данные, которые находятся в одном столбце или одной строке. Сегмент круга – это доля каждого элемента массива в сумме всех элементов.
С помощью любой круговой диаграммы можно показать распределение в том случае, если
- имеется только один ряд данных;
- все значения положительные;
- практически все значения выше нуля;
- не более семи категорий;
- каждая категория соответствует сегменту круга.
На основании имеющихся данных о количестве осадков построим круговую диаграмму.
Круговая диаграмма распределения осадков по сезонам года лучше смотрится, если данных меньше. Найдем среднее количество осадков в каждом сезоне, используя функцию СРЗНАЧ. На основании полученных данных построим диаграмму:
Получили количество выпавших осадков в процентном выражении по сезонам.
В двух словах: Добавляем полосу прокрутки к гистограмме или к графику распределения частот, чтобы сделать её динамической или интерактивной.
Уровень сложности: продвинутый.
На следующем рисунке показано, как выглядит готовая динамическая гистограмма:
Что такое гистограмма или график распределения частот?
Гистограмма распределения разбивает по группам значения из набора данных и показывает количество (частоту) чисел в каждой группе. Такую гистограмму также называют графиком распределения частот, поскольку она показывает, с какой частотой представлены значения.
В нашем примере мы делим людей, которые вызвались принять участие в мероприятии, по возрастным группам. Первым делом, создадим возрастные группы, далее подсчитаем, сколько людей попадает в каждую из групп, и затем покажем все это на гистограмме.
На какие вопросы отвечает гистограмма распределения?
Гистограмма – это один из моих самых любимых типов диаграмм, поскольку она дает огромное количество информации о данных.
В данном случае мы хотим знать, как много участников окажется в возрастных группах 20-ти, 30-ти, 40-ка лет и так далее. Гистограмма наглядно покажет это, поэтому определить закономерности и отклонения будет довольно легко.
Возможно, мы захотим немного изменить детализацию картины и разбить население на две возрастные группы. Это покажет нам, что в мероприятии примут участие большей частью молодые люди:
Динамическая гистограмма
После построения гистограммы распределения частот иногда возникает необходимость изменить размер групп, чтобы ответить на различные возникающие вопросы. В динамической гистограмме это возможно сделать благодаря полосе прокрутки (слайдеру) под диаграммой. Пользователь может увеличивать или уменьшать размер групп, нажимая стрелки на полосе прокрутки.
Такой подход делает гистограмму интерактивной и позволяет пользователю масштабировать ее, выбирая, сколько групп должно быть показано. Это отличное дополнение к любому дашборду!
Как это работает?
Формулы
Чтобы всё работало, первым делом нужно при помощи формул вычислить размер группы и количество элементов в каждой группе.
Чтобы вычислить размер группы, разделим общее количество (80-10) на количество групп. Количество групп устанавливается настройками полосы прокрутки. Чуть позже разъясним это подробнее.
Далее при помощи функции ЧАСТОТА (FREQUENCY) я рассчитываю количество элементов в каждой группе в заданном столбце. В данном случае мы возвращаем частоту из столбца Age таблицы с именем tblData.
Функция ЧАСТОТА (FREQUENCY) вводится, как формула массива, нажатием Ctrl+Shift+Enter.
Динамический именованный диапазон
В качестве источника данных для диаграммы используется именованный диапазон, чтобы извлекать данные только из выбранных в текущий момент групп.
Когда пользователь перемещает ползунок полосы прокрутки, число строк в динамическом диапазоне изменяется так, чтобы отобразить на графике только нужные данные. В нашем примере задано два динамических именованных диапазона: один для данных — rngGroups (столбец Frequency) и второй для подписей горизонтальной оси — rngCount (столбец Bin Name).
Элемент управления Полоса прокрутки (Scroll Bar) может быть вставлен с вкладки Разработчик (Developer).
На рисунке ниже видно, как я настроил параметры элемента управления и привязал его к ячейке C7. Так, изменяя состояние полосы прокрутки, пользователь управляет формулами.
Гистограмма
График – это самая простая часть задачи. Создаём простую гистограмму и в качестве источника данных устанавливаем динамические именованные диапазоны.
Есть вопросы?
Что ж, это был лишь краткий обзор того, как работает динамическая гистограмма.
Да, это не самая простая диаграмма, но, полагаю, пользователям понравится с ней работать. Определённо, такой интерактивной диаграммой можно украсить любой отчёт.
Более простой вариант гистограммы можно создать, используя сводные таблицы.

Пускай имеем систему линейных уравнений:
1. Запишем коэффициенты системы уравнений в ячейки A1:D4 а столбец свободных членов в ячейки E1:E4 . Если в ячейке A1 находится 0, необходимо поменять строки местами так, чтоб в этой ячейке было отличное от ноля значение. Для большей наглядности можно добавить заливку ячеек, в которых находятся свободные члены. (скриншот)
2. Необходимо коэффициент при x1 во всех уравнениях кроме первого привести к 0. Для начала сделаем это для второго уравнения. Скопируем первую строку в ячейки A6:E6 без изменений, в ячейки A7:E7 необходимо ввести формулу: <=A2:E2-$A$1:$E$1*(A2/$A$1)>. Таким образом мы от второй строки отнимаем первую, умноженную на A2/$A$1, т.е. отношение первых коэффициентов второго и первого уравнения. Для удобства заполнения строк 8 и 9 ссылки на ячейки первой строки необходимо использовать абсолютные (используем символ $). (скриншот)
3. Копируем введенную формулу формулу в строки 8 и 9, таким образом избавляемся от коэффициентов перед x1 во всех уравнениях кроме первого. (скриншот)
5. Осталось привести коэффициент при x3 в четвертом уравнении к 0, для этого вновь проделаем аналогичные действия: скопируем полученные 11, 12 и 13-ю строки (только значения) в строки 16-18, а в ячейки A19:E19 введем формулу <=A14:E14-$A$13:$E$13*(C14/$C$13)>. Таким образом реализуется разность строк 14 и 13, умноженных на коэффициент C14/$C$13 . Не забываем проводить перестановку строк, чтоб избавиться от 0 в знаменателе дроби. (скриншот)
6. Прямая прогонка методом Гаусса завершена. Обратную прогонку начнем с последней строки полученной матрицы. Необходимо все элементы последней строки разделить на коэффициент при x4. Для этого в строку 24 введем формулу . (скриншот)
7. Приведем все строки к подобному виду, для этого заполним строки 23, 22, 21 следующими формулами:
23: — отнимаем от третьей строки четвертую умноженную на коэффициент при x4 третьей строки.
22: — от второй строки отнимаем третью и четвертую, умноженные на соответствующие коэффициенты.
21: — от первой строки отнимаем вторую, третью и четвертую, умноженные на соответствующие коэффициенты.
Результат (корни уравнения) вычислены в ячейках E21:E24 . (скриншот)
UPDATE от 25 апреля 2012 г. Выкладываю xls-файл с решением линейных уравнений методом Гаусса в Microsoft Excel: Показать ссылку
Читайте также: