Как сделать координатную
Программа "Рисуем по координатам" является хорошим наглядным инструментом для создания (построения) рисунков и фигур по координатам на координатной плоскости (сетке). Все точки рисунка (картинки) наносятся по координатам в порядке их следования. После чего соединяем линией точки. В результате получится заданный рисунок (фигура) на координатной плоскости по координатам.
Программа "Рисуем по координатам" предназначена для рисования разной сложности рисунков (легкие, простые, сложные). и построения различных фигур по координатам точек на координатной плоскости и подойдет для 4, 5, 6 классов. Она позволяет наглядно увидеть, как можно использовать математику для построения (рисования) различных рисунков (картинок); животные, птицы, цветы, листья, деревья, машины, самолеты, ракеты, грибы, пауки, корабли, змеи, рыбки и другие.
СБОРНИК РИСУНКОВ И ФИГУР ПО КООРДИНАТАМ
В сборнике представлены рисунки и фигуры по координатам на клетчатом поле (сетке) в прямоугольной системе координат, где принято, что единичный отрезок 1 клетка. Для удобства выбора задания по возрасту, по способности и познавательным интересом, все задания представлены различного уровня сложности (легкие, простые, сложные) и имеют разную тематику. Можно научиться и самому создавать любой рисунок по координатам. Все готовые рисунки и картинки по координатам можно бесплатно и без регистрации скачать и распечатать на листе формата А4.
Рисование по координатам точек на координатной плоскости (сетке) это не только увлекательное занятие, но и поучительное как в области рисования, так и в математике. Программа "Рисуем по координатам" предназначена для использования, как на уроках математики, так и для организации интересного досуга дома. Саму же программу можно бесплатно скачать здесь.
Существует и другой способ создать рисунок (фигуру) по координатам не в программе "Рисуем по координатам", а на клетчатом поле. Данная тема интересна тем, что в координатной плоскости на клетчатом поле можно строить не только различные графики функций, но и увидеть связь природной красоты и строгой математики, создавая красивые рисунки и фигуры по координатам своими руками.
КАК РИСОВАТЬ ПО КООРДИНАТАМ
Рисунки и фигуры на координатной плоскости строятся по точкам. Каждая точка на плоскости имеет две координаты и записывается в виде двух чисел X (икс) и Y (игрек) через точку с запятой в скобках, например точка A (х; у), где первая цифра обозначает расстояние, отложенное от центра системы координат по оси X (икс), вторая цифра расстояние, отложенное от центра по оси Y (игрек). Рассмотрим построение координатных точек на координатной плоскости (сетке) на реальном примере.
Для этого нужно взять либо обычный лист из тетради в клеточку, либо распечатать готовый лист А4 в клетку его можно скачать здесь. Создаём прямоугольную систему координат. Для этого, рисуем координатные оси X и Y, где принимаем за единичный отрезок 1 клетку и для удобства нумеруем цифрами, как показано на рисунке. Можно распечатать уже готовый лист А4 в клетку с осями координат и с числами здесь. . Вот теперь все готово и можно приступать.
Возьмем для примера первую координату точку A (2;5) нашего рисунка или картинки и отложим эти расстояния по координатным осям X и Y. Первое число 2 мы отложим по оси X, а второе значение нашей координаты число 5 по координатной оси Y. В пересечении двух мысленно проведенных перпендикулярных линий к осям координат (они обозначены пунктирной линией на рисунке), мы получим нашу первую точку A (2;5).
Таким же методом строим координаты второй точки, третьей и так далее. После построения всех точек мы соединяем прямой линией первую точку со второй, вторую с последующей точкой в порядке их следования. После соединения всех точек мы получим заданный рисунок (фигуру) по своим координатам.
Чтобы найти координаты любой точки рисунка (фигуры) на плоскости, необходимо создать координатную плоскость на этом рисунке и опустить из этой точки перпендикуляры на координатные оси X и Y. Эти два значения и будут ее координаты.
РИСУНКИ ПО КООРДИНАТАМ ДЛЯ НАЧИНАЮЩИХ
В сборнике представлены различные рисунки на координатной плоскости с координатами для разного возраста. Рисунки (фигуры) по координатам для начинающих были построены или взяты из различных источников: журналов, интернет-ресурсов. Данный материал можно использовать как карточки с заданиями с целью закрепления материала. Все рисунки (фигуры) по координатам можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.
ЛЕГКИЕ РИСУНКИ
ПРОСТЫЕ РИСУНКИ
СРЕДНИЕ РИСУНКИ
РИСУНКИ ПО КООРДИНАТАМ СЛОЖНЫЕ И КРАСИВЫЕ
В сборнике представлены красивые и сложные рисунки на координатной плоскости с координатами для разных возрастных групп. Все красивые рисунки (картинки) по координатам после построения можно еще и раскрашивать красками, карандашами и фломастерами. Красивые и сложные рисунки по координатам показывают, что можно совершенствовать линии контура рисунков и реализовывать свои фантазии безгранично. Лист А4 в клетку и координатные сетки при необходимости можно скачать здесь.
СОБАКИ
КООРДИНАТЫ ДЛЯ РИСУНКОВ
В сборнике представлены различные примеры наборов координат без рисунка, по которым надо восстановить рисунок. Для этого необходимо на чистом листе в клетку востановить по координатам исходный рисунок. Представленные наборы имеют разную сложность и будут интересны для разных возрастных групп. Любой материал можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку при необходимости можно скачать здесь.
ЛЕГКИЕ РИСУНКИ
ПРОСТЫЕ РИСУНКИ
СЛОЖНЫЕ РИСУНКИ
ДОРИСУЙ ВТОРУЮ ПОЛОВИНУ
В сборнике дорисуй вторую половину, все картинки представляют собой незаконченный симметричный рисунок, выполненный на клетчатом поле с одной стороны оси. Необходимо дорисовывать вторую половину рисунка соблюдая симметрию. Дорисуй вторую половину начинать рисовать надо от простых рисунков по клеткам к более сложным. Данное задания развивает зрительное восприятие, произвольное внимание, пространственное мышление, усидчивость и внимание к деталям, а также тренирует мелкую моторику и координацию движений руки. Лист А4 в клетку при необходимости можно скачать здесь.
ПРОСТЫЕ РИСУНКИ
СЛОЖНЫЕ РИСУНКИ
ПОВТОРИ КРАСИВЫЕ РИСУНКИ ПО ОБРАЗЦУ
В сборнике красивые рисунки по образцу, представлены различные примеры рисунков без координат на клетчатом поле для разных возрастных групп. Можно повторить рисунок по образцу на чистом листе А4 в клетку, а можно добавить оси координат и перевести рисунок в координаты. Все красивые рисунки по образцу можно дорабатывать и фантазировать под свой вкус. Любой красивый рисунок по образцу можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.
КРАСИВЫЕ РИСУНКИ
МАШИНЫ
КАРТОЧКИ РИСУНКОВ
В сборнике карточки рисунков представлены разные рисунки и фигуры различной сложности. В карточках можно либо повторить рисунок рядом на чистом поле в клетку, либо написать координаты этого рисунка. Данный материал можно использовать как учебные карточки для закрепления пройденного материала, самостоятельных работ и различных конкурсов и викторин. Все карточки сборников рисунков по координатам можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.
СБОРНИК
ДОРИСУЙ РИСУНКИ ПО ОБРАЗЦУ
В сборнике рисунки по образцу представлены примеры рисунков различной сложности, которые можно либо дорисовать рисунок по образцу, либо рядом на чистом листе в клетку нарисовать его полностью глядя на образец. Дорисуй рисунки по образцу подойдут для использования разного возраста. Все рисунки по образцу можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.
ЛЕГКИЕ РИСУНКИ (СБОРНИКИ)
ПРОСТЫЕ РИСУНКИ
НАРИСУЙ КАРТИНКИ ПО КЛЕТКАМ И РАСКРАСЬ
В сборнике нарисуй картинки по клеткам и раскрась, представлены как отдельные картинки, так и примеры сборников рисунков различной сложности, которые можно перерисовать по образцу на чистом листе в клетку, а при желании и раскрасить. Картинки по клеткам будут интересны для разного возраста. Любые рисунки (картинки) по клеткам можно бесплатно и без регистрации скачать в формате pdf и распечатать на листе формата А4. Лист А4 в клетку или координатные сетки при необходимости можно скачать здесь.
ПРОСТЫЕ РИСУНКИ
РИСУНКИ (СБОРНИКИ)
ЛИСТ А4 В КЛЕТКУ. МИЛЛИМЕТРОВКА А4
Чистый лист А4 в клетку, координатная сетка для печати или миллиметровая бумага может понадобиться при рисования рисунков по координатам, картинок по образцу и других видов работ. Все пустые листы в клетку и миллиметровки расположены на листе формата A4 и их можно свободно скачать. Листы в клетку представлены; в темную клетку (черная), светлую клетку (серая), с осями координат и с числами. Листы миллиметровой бумаги представлены в 4-х вариантах; blue (синяя), green (зеленая), orange (оранжевая), pink (розовая).
ВОЗМОЖНОСТИ ПРОГРАММЫ
Программа "Рисуем по координатам" имеет два режима:
- Рисует на доске изображение по введенной Вами таблице точек координат, печатает в цвете таблицу и рисунок;
- Составит таблицу координат по нарисованному на доске изображению.

Загрузите примеры рисунков или скачайте с моего сайта и попробуйте дорисовать в них что-нибудь, или изобразите самостоятельно какой-нибудь домик, Вы увидите, как это здорово.

Этот сборник заданий поможет не только любому учителю организовать творческий подход к изучению данной темы, но и получить хорошие результаты в её усвоении.
Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.

Эти прямые называют осями координат, точку их пересечения О - начало отсчета.
Горизонтальная ось - ось абсцисс, обозначают буквой , поэтому еще называют ось , пишут: .
Вертикальная ось - ось ординат, обозначают буквой , поэтому еще называют ось , пишут: .
Оси и вместе образуют прямоугольную систему координат на плоскости. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.
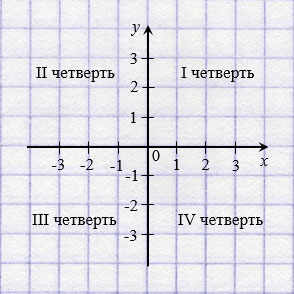
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ ), и прямую АС, перпендикулярную оси ординат (АС ).
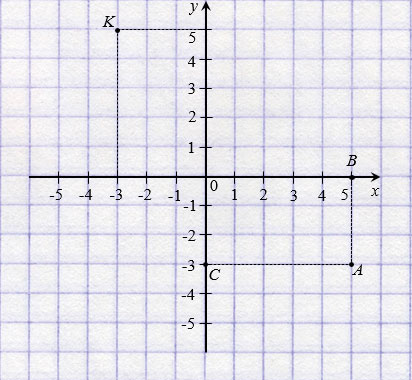
Точка В на оси имеет координату 5, а точка С на оси - координату 3 . Число 5 называют абсциссой точки А, число 3 - ординатой точки А. Числа 5 и 3 однозначно определяют положение точки А на координатной плоскости, поэтому их называют координатами точки А и записывают: А(5; 3).
Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату - на второе. Если числа 5 и 3 поменять местами, то получим координаты другой точки - точки К( 3; 5) (смотри рисунок выше).

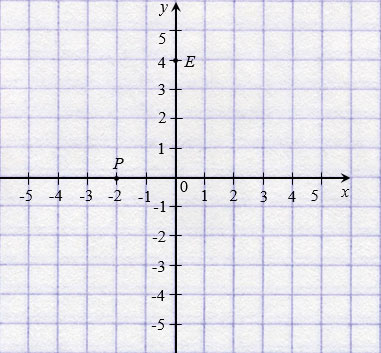
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р(2; 0); Е(0; 4).
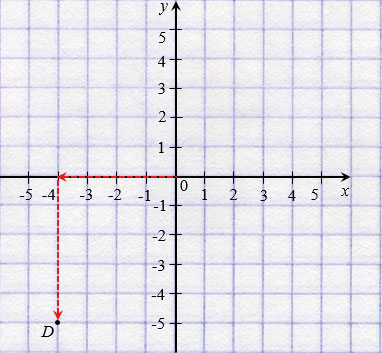
Чтобы попасть в точку D с координатами (4; 5), нужно сначала пройти по оси от начала отсчета влево на 4 единицы, а потом - на 5 единиц вниз.
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
На рисунке ниже точки N(2; 4) и М( 2; 4) симметричны относительно начала координат.

Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.

На рисунке ниже точки Р(3; 2) и К(3; 2) симметричны относительно оси ординат.
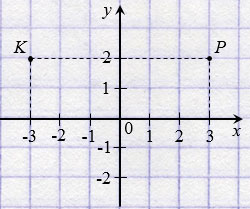
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.

На рисунке ниже точки Р(3; 2) и Е(3; 2) симметричны относительно оси абсцисс.

Современные технологии позволяют в несколько кликов поделиться с другом нашим месторасположением. Достаточно зайти в гугл карты и пошерить координаты точки. В этом материале узнаем, как такое же действие отобразить на бумаге.
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):

- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Приветствую, друзья! Сегодня я поделюсь с Вами информацией, как построить в Ворде график функции. В Интернете много примеров построения диаграмм с использованием Ворда и Экселя, но данные приемы не всегда могут соответствовать конечному результату.
Например, чтобы построить график функции по точкам, нужно заполнить таблицу данными, затем построить диаграмму типа График. Далее необходимо провести кучу дополнительных настроек, чтобы привести этот график к нужному виду.
И скажите, зачем столько трудностей, когда нужен всего-то рисунок этого графика для иллюстрации функции. Следовательно, проще взять и нарисовать этот график средствами векторного редактора, встроенного в Word.
Итак, давайте на примере параболы разберем, как построить в Ворде график этой функции. Если быть кратким, то сначала нарисуем график, а потом сохраним его как картинку и вставим в нужный документ. Я использую версию Word 2016, но все шаги вполне применимы и в более ранних версиях, так как отличия в интерфейсе минимальны.
Как построить в Ворде график функции по точкам
Создадим новый документ (Файл – Создать — Новый документ – Создать).
Для рисования графика по точкам, хорошо бы воспользоваться сеткой. Включаем её.
На вкладке Вид в разделе Показать ставим галочку напротив пункта Сетка. Теперь гораздо проще будет рисовать координатные оси и сам график.
Рисуем оси координат
На вкладке Вставка в разделе Фигуры-Линии выбираем Стрелку. Курсор примет вид крестика. При нажатой левой кнопке мыши растягиваем стрелку до нужной длины.
При выделенной фигуре, на ее концах есть кружки. Потянув за любой из них, при нажатой левой кнопке мыши, можно изменить длину или направление стрелки.
Для рисования второй оси проделываем шаги, описанные выше.
Далее определяем на нашей сетке единичный отрезок и обозначаем его с помощью надписи (Вставка – Надпись – Нарисовать надпись). Растягиваем небольшой прямоугольник и вписываем в него цифру 1. Теперь убираем заливку и контур у надписи (фигура Надпись должна быть выделена). В ленте меню выбираем Средства рисования – Формат и в разделе Стили фигур выбираем для Заливки фигуры – Нет заливки, а для Контура фигуры – Нет контура. Теперь контур и заливка станут прозрачными.

Остается только перенести цифру поближе к нужному месту.
Если скопировать эту надпись и вставить несколько раз, то можно будет, заменив единичку, подписать оси координат, указать начало координат и расставить еще несколько значений на осях.
Ну, вот, координатная плоскость задана.
Рисуем график параболы у=х 2
В фигурах выбираем Кривая и на нашей координатной плоскости делаем одним кликом первую точку(-3,9), следующий клик в точке(-2,4), следующий в точке (-1,1) и так далее. На последней точке делаем двойной клик, чтобы завершить рисование кривой. Желательно постараться проставить все нужные точки графика за один проход.


Ваши узловые точки будут доступны для перемещения, можно скорректировать кривизну или длину кривой. Используя контекстное меню для кривой, узлы можно добавить или удалить.
Изменить цвет графика и его толщину можно в ленте меню Средства рисования – Формат и в разделе Стили фигур.
Теперь, когда график готов, нужно сделать его скриншот и вставить в нужный документ.
Как сделать скриншот в Ворде
Изменяем масштаб страницы так, чтобы рисунок графика занял максимальную область экрана. На клавиатуре нажимаем кнопку PrintScreen(PrtSc). Затем идем в нужный документ указываем место для вставки и даем команду Вставить из вкладки Главная на ленте инструментов или из контекстного меню. Вставится все содержимое экрана с ненужными нам частями.
Выполним обрезку. Кликаем по рисунку. На вкладке Работа с рисунками – Формат в разделе Размер выбираем инструмент Обрезка. Изменяем размер видимой области с помощью черных угловых маркеров и нажимаем кнопку Enter на клавиатуре для применения обрезки. Увеличить полученное изображение можно, потянув за угловые кружочки.
Теперь Вы знаете как построить в Ворде график. Этот способ я часто использую для рисования графиков или несложных рисунков в Ворде. Надеюсь, в Вашей копилке знаний он тоже не будет лишним. Вы можете поделиться с друзьями полученной информацией. Кнопочки социальных сетей ниже.
Мы, учителя, постоянно в поиске: как, не меняя содержание материала, найти способы овладения им и его применения, как заинтересовать учащихся в изучении данной темы, как сформировать у них прочные знания. При изучении темы “Координатная плоскость” можно подойти творчески, по данным координатам точек можно нарисовать знакомую картинку. Такие задания увлекают детей, заинтересовывают, и многие сами затем с удовольствием составляют рисунки по координатам. Эта творческая работа носит и воспитательный характер.
Мною и детьми были составлены данные задания, а некоторые из них взяты из еженедельной учебно-методической газеты “Математика”. На координатной плоскости отмечаем точки, заданные своими координатами, в порядке их следования. А затем соединяем каждую точку с предыдущей кривой или отрезком. Что в результате получится, вы увидите в итоге.
Этот сборник заданий поможет любому учителю организовать творческий подход к изучению данной темы и получить хорошие результаты в её усвоении.
(-5; 4), (-7; 4), (-9; 6), (-11; 6), (-12; 5), (-14; 5), (-12; 4), (-14; 3), (-12; 3), (-11; 2), (-10; 2),
(-9; 1), (-9; 0), (-8; -2), (0; -3), (3; -2), (19; -2), (4; 0), (19; 4), (4; 2), (2; 3), (6; 9), (10; 11), (3; 11), (1; 10), (-5; 4), глаз (-10,5; 4,5).
(3; 0), (1; 2), (-1; 2), (3; 5), (1; 8), (-3; 7), (-5; 8), (-3; 4), (-6; 3), (-3; 3), (-5; 2),(-5; -2), (-2; -3), (-4; -4), (1; -4), (3; -3), (6; 1), (3; 0) и (-1; 5).
(-1; 4), (-2; 1), (-3; 2), (-4; 2), (-4; 3), (-6; 4), (-6; 6), (-8; 9), (-7; 10), (-6; 10), (-6; 11), (-5; 10), (-4; 10), (-3; 9), (-1; 9,5), (1; 9), (3; 10), (4; 11), (4; 16), (3; 18), (5; 17), (6; 17), (5; 16), (6; 12), (6; 9), (4; 7), (1; 6),
(2; 5), (5; 4), (5; 3), (4; 4), (1; 2), (1; 0), (3; -4), (4; -5), (1;-7), (1; -6), (0; -4), (-2; -7), (-1,5; -8), (-5; -7), (-4; -6), (-5; -4), (-7;-5), (-7; -7), (-6,5; -8), (-10,5; -8), (-10; -7), (-10; -6), (-11; -7),
(-11; -8), (-14; -6), (-13; -5), (-12; -3), (-13; -2), (-14; -3), (-12; 1), (-10; 3), (-8; 3), (-6; 4), глаз (-1; 7).
(-10; -2), (-11; -3), (-10,5; -5), (-11; -7), (-12; -10), (-11; -13), (-13; -13), (-13,5; -7,5), (-13; -7), (-12,5; -5), (-13; -3), (-14; -1), (-14; 4), (-15; -6), (-15; -3), (-14; 2), (-11; 4), (-10; 8), (-8; 9),
(5;1), (6;2), (6;3), (5;6), (4;7), (5;8), (6;8), (8;9), (9;9), (7;8), (9;8), (6;7), (7;6), (9;6), (11;5), (12;3), (12;2), (13;3), (12;1), (7;1), (8;2), (9;2), (8;3), (6;1), (5;1) и (5;7).
Читайте также:


