Как сделать координатную прямую из картона своими руками 6 класс
Тип урока: Урок получения новых знаний
Цели: Обучающие: ввести понятие координатной прямой, координаты точки, научить отмечать точки на координатной прямой.
развивающие: развитие умения анализировать, сравнивать, обобщать, проводить аналогию, делать выводы.
воспитывающие: воспитывать интерес к математике, дисциплинированность, ответственное отношение к учебному труду.
Планируемые образовательные результаты: Предметные: Умение отмечать точки на координатной прямой и записывать координаты точки.
Личностные: положительная мотивация к математической деятельности, адекватную самооценка по владению новым материалом
Регулятивные – уметь определять и формулировать цель на уроке с помощью учителя, проговаривать последовательность действий на уроке, работать по коллективно составленному плану, оценивать правильность выполнения действий, планировать свое действие в соответствии с поставленной задачей.
Коммуникативные – уметь оформлять свои мысли в устной форме, слушать и понимать речь других. Совместно договариваться о правилах поведения и общения в школе и следовать им.
Познавательные – уметь ориентироваться в своей системе знаний. Добывать новые знания; уметь структурировать знания.
Технологическая карта урока
Деятельность учителя
Деятельность учащихся
1. Самоопределение к деятельности. Организационный этап урока
Именно этим мы с вами сегодня будем заниматься на уроке. Мы будем учиться размышлять, получая тем самым новые знания. А познакомимся мы с вами на уроке с очень важными понятиями, которые вы будете применять на протяжении всего обучения в школе, причем не только на уроках математики, но и на других предметах тоже и в практической деятельности.
Запишите в тетрадях число и оставьте место для темы урока, ее мы запишем позже.
Учащиеся приветствуют учителя. Включаются в деловой ритм урока.
2. Этап актуализации и фиксирования индивидуального затруднения в пробном действии.

- Ребята, какая геометрическая модель изображена на рисунке?
Назовите ее составляющие.
Как называются числа, соответствующие данным точкам?
Назовите координаты указанных точек.
Какую координату будет иметь точка А, если ее переместить
А) на 3 единичных отрезка вправо;
В) на 6 единичных отрезков влево. (Создалась проблемная ситуация)
Отвечают на вопрос
Анализируют информацию. Высказывают предположения.
Ответы на вопросы.
3. Этап выявления места и причины затруднения.
Почему? Нужны новые знания, нужна другая геометрическая модель, т.к. с помощью этой модели ответить на 2-й вопрос нельзя. Вот если бы можно было продолжить этот луч в другую сторону…
Учащиеся признаются в том, что не могут ответить на вопрос.
Не хватает знаний.
4. Этап построения проекта выхода из затруднения.
- Ребята. Вот сегодня мы и познакомимся с координатами на прямой. Догадываетесь, какая будет сегодня тема урока?
- Что вы должны узнать сегодня на уроке?
- Чему должны научиться?
- Все верно. Сегодня мы познакомимся с координатной прямой и новыми числами на ней.
- Координаты на прямой.
- Есть ли другая геометрическая модель, кроме координатного луча, которая получается после продолжения луча влево.
- Находить координаты точек не только справа, но и слева от нуля).
5. Этап реализации построенного проекта.
Что такое координатная прямая?
Что называют координатой точки на прямой?
Какими числами являются координаты точек на горизонтальной прямой, расположенных: а) справа от начала координат? ;б) слева от начала координат?
Какую координату имеет начало координат?
Какими числами обозначают координаты точек на вертикальной прямой, расположенных: а) выше начала координат; в) ниже начала координат?
- Давайте вернемся к затруднению в начале урока. Ответьте на 2-й вопрос. Для этого начертите координатную прямую.
Число 0 относится к положительным или отрицательным числам?
(учитель выслушивает ответы и предлагает подготовленному ребенку рассказать стихотворение о нуле).
- А где в окружающей обстановке вы встречаетесь с координатной прямой?
Дети изучают тему, затем отвечают на вопросы.
Отвечают на вопрос
Стихотворение о нуле
Когда- то многие считали,
что нуль не значит ничего
И, как ни странно, полагали
Что нуль совсем не есть число
Но на прямой, средь прочих чисел
Он все же место получил,
И все действительные числа
На два разряда разделил.
6. Первичное закрепление нового знания
Дети с проговариванием решают задание № 846, 850
7. Самостоятельная работа и проверка по эталону.
1. Начертите координатную прямую, приняв за единичный отрезок пять клеток тетради. Отметьте на этой прямой точки А (2), B (-3), C (-1), D (1,2), E (-2/5), F (-2,6), M (-1¼).
2. Запишите координаты точек A , M , K и P изображенных на рисунке:

3. Начертите горизонтальную прямую и отметьте на ней точку A . Правее точки A на расстоянии 3 см. отметьте точку B . Отметьте точку O – начало отсчета, если A (- 6), а B (- 3).
1. Начертите координатную прямую, приняв за единичный отрезок длину четырех клеток тетради. Отметьте на этой прямой точки А (3), B (-2), C (2,5), D (1,5), E (-2,75), F (-3 2/5), M (-¼).
2. Запишите координаты точек M , N , K и D изображенных на рисунке:

3. Начертите горизонтальную прямую и отметьте на ней точки C и D так, чтобы D была правее точки C и CD = 5 см. Отметьте точку O – начало отсчета, если C (-2), а D (3).
Выполняют работу. Проверяют по эталону.
8. Включение в систему знаний и умений и повторения.
Учитель предлагает устно решить тест:
1. Термометр показывает температуру 3°С. Какую температуру будет показывать термометр, если температура понизится на 2°С? А: 3°С, Б:5°С, В:1°С
2. Число 0 является:
А: положительным числом
Б: отрицательным числом
В: ни положительным, ни отрицательным числом.
3. Какое из чисел 4,5; 0,3; -4,5; -0,3 расположено на координатной прямой правее других?
А: -4,5 Б: 0,3 В: 4,5 Г: -0,3
9. Рефлексия. Задание на дом.
Учитель предлагает детям закончить предложение:
- сегодня на уроке я познакомился с…
- мне очень понравилось…
- у меня хорошо получилось…
- у меня возникли сложности с…
- я ухожу с урока с… настроением.
Д/з: изучить § 30, вопросы 1–4, № 847, 849, 851.
Творческое задание: - Человек обладает положительными и отрицательными качествами. Распределите эти качества на координатной прямой. К чему должен стремиться человек? Какими Качествами, которых у вас нет, вы бы хотели обладать?
В этом уроке Вы узнаете, что такое координатная прямая, научитесь на ней обозначать положительные и отрицательные числа, определять координаты симметричных точек.
Давайте возьмем координатный луч.
На нем отмечено начало – точка О, единичный отрезок и справа от начала координат у нас находятся положительные числа в порядке возрастания.
А где расположить отрицательные?
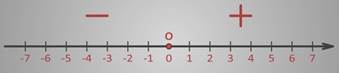
Чтобы отметить отрицательные числа нужно луч дополнить противоположным ему лучом и нанести на него такие же деления.
Таким образом, получилась координатная прямая.
Справа от точки О – начала координат – находятся положительные числа, а слева – отрицательные.
Следовательно, координатная прямая – это прямая с указанным на ней началом отсчета, направлением отсчета и единичным отрезком.
Координата – число, показывающее положение точки на координатной прямой.
Числа, расположенные справа от точки О на координатной прямой – положительные, соответственно направление, в котором они расположены называют положительным.
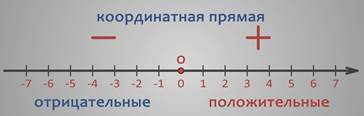
Числа, которые расположены слева – отрицательные, поэтому направление, в котором они расположены называется отрицательным.
На координатной прямой стрелкой указывается только положительное направление. Число 0 разделяет положительные и отрицательные числа.
Каждому числу соответствует единственная точка прямой.
Например, числу 3,5 соответствует точка М, которая удалена от начала отсчета, т. е. от точки О, на расстояние, равное 3,5 (в заданном масштабе), и отложена от точки О в заданном (положительном) направлении.
Числу -4 соответствует точка Р , которая удалена от точки О на расстояние, равное 4, и отложена от точки О в отрицательном направлении, т. е. в направлении, противоположном заданному.
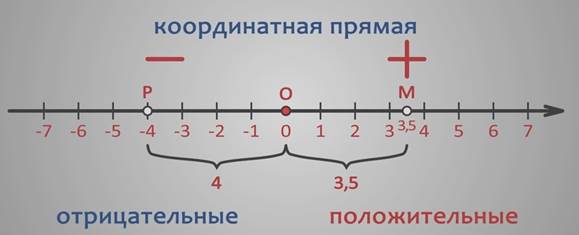
Верно и обратное: каждая точка координатной прямой соответствует единственному числу.

Около стрелки, указывающей направление отсчета на координатной прямой, часто ставят буквы x, y или t .

Координатные прямые могут располагаться на плоскости по-разному, не только горизонтально.
Например, шкалу на термометре можно назвать координатной прямой.
Она будет вертикальной.
В этом случае положительные числа будут находиться выше 0, а отрицательные ниже 0.
Выполним практическое задание:

Изобразим координатную прямую.
Отметим на координатной прямой точки А (3), В (-3).
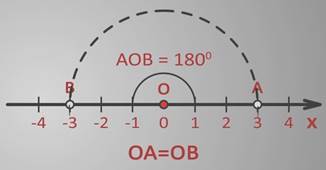
Обратите внимание: расстояние от точки А до начала координат точки О будет равно расстоянию OB.

точки А и В будут центрально-симметричны относительно начала отсчета координатной прямой точки О (0).
Следует отметить, что центром симметрии точек на координатной прямой может быть любая точка данной прямой.
Поучимся находить симметричные точки на координатной прямой.
Пусть точка О (0) – центр симметрии.
Найдем точку, симметричную точке С (-6).
Такой точкой будет точка расположенная по другую сторону от центра симметрии.

Центром симметрии теперь будет точка А (-2).
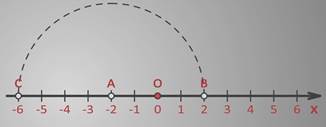
Между точками С (-6) и А (-2) – четыре единичных отрезка.
Отсчитаем от точки А (-2) четыре единичных отрезка вправо отметим точку В.
Определим ее координату – (2).
Таким образом, точки С (-6) и В (2) будут центрально-симметричны относительно точки А (-2).
А как определить координату центра симметрии двух точек на координатной прямой?
Пусть даны симметричные точки М(-1,4) и М1(2,6).
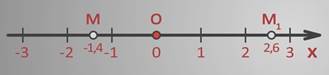
Расстояние от точки М до О(0) 1,4, от М1 до начала координат – 2,6.
Центр симметрии должен быть посередине.



Таким образом, в этом уроке Вы узнали, что такое координатная прямая, научились определять координаты точек и находить симметричные точки.

Урок преднозначен для получения новых знаний по теме "координатная прямая". данная разработка способствует формированию навыков построения координатных прямых с различными значениями еденичного отрезка. Выробатывает навыки нахождения координаты точки на прямой. Урок преднозначен для 6 класса.
Координатная прямая 6 класс
Цели урока: 1. Сформировать у учащихся представление о координатной прямой.
2. Способствовать формированию у учащихся навыков построения
координатных прямых с различными значениями величины
единичного отрезка, навыков определения координат точек,
расположенных на координатной прямой.
3. Научить строить точки на координатной прямой по
4. Развивать мышление, умение анализировать,
сопоставлять и формулировать выводы
Оборудование: интерактивная доска, проектор, компьютер учителя, компьютеры
План урока: I . Организационная часть.
II . Актуализация знаний в ходе проверки домашнего задания.
III . Усвоение нового материала в ходе работы с использованием
IV. Закрепление изученного при индивидуальной работе с модулями
V . Подведение итогов.
VI . Домашнее задание.
I .Организационный момент
II . Актуализация знаний в ходе проверки домашнего задания
Цель: Проверить качество навыков учащихся по:
определению координат точек на координатном луче
построению точек на координатном луче по заданным координатам
построению координатного луча с единичным отрезком равным m см.
Обратить особое внимание учащихся на произвольность и целесообразность выбора длины единичного отрезка
Фронтальная проверка выполнения домашнего задания №1 и №2 с использованием
На доске открывается файл Д-З

Проверка Задания 1.
Учащийся выходит к доске и показывает на ней свой вариант выполнения первого задания домашней работы. Нужные числа из зелёного прямоугольника переносит в скобки. После обсуждения правильности выполнения и внесения возможных поправок на доске в тетрадях, переходят к выполнению Задания №2.
Проверка Задания 2.
Точки A , B и C являются перемещаемыми и переносятся при нажатии на них пальцем, в необходимую точку на координатной прямой.
Второй учащийся переносит точки на координатный луч, дублируя чертёж из домашней работы. Учащиеся класса обсуждают правильность выполнения, при необходимости вносят свои поправки на доске или в своих тетрадях.
Обращаем внимание учащихся на целесообразность выбора длины единичного отрезка. Устно рассматриваем вопрос:
Какой длины единичный отрезок лучше выбрать для изображения на координатном луче точек A ( 2/5), B ( 1/5) и С(7/5)?
III . Изучение нового материала в ходе работы на интерактивной доске.
Для размещения отрицательных чисел координатного луча уже не достаточно. Его необходимо дополнить до прямой, отложить единичные отрезки слева от его начальной точки. Координатный луч превратится в координатную прямую.
Постановка обучающих целей урока.

На доске переходим ко второму слайду

Начальная точка О(0) и единичный отрезок являются перемещаемыми и учитель последовательно показывает:
Выбор начальной точки
Выбор положительного направления
Разметку прямой путём последовательного откладывания единичного отрезка и расстановки целых положительных и отрицательных чисел под соответствующими штрихами
Обращаем внимание учащихся на то, как записываются и как читаются координаты точек.

Р
абота по формированию навыков определения координат точек и их записи
На доске переходим к третьему слайду.
Учащийся работает у доски и расставляет перемещаемые значения координат точек, зафиксированных на координатной прямой
Самопроверка после выполнения задания производится путём сравнения при открытии закрытого текста

4.Формирование навыков построения точек по их координатам
Слайд 4. Построение точек по их заданным координатам путём их размещения на координатной прямой

Учащиеся работают у доски и располагают точки на координатной прямой путём их перетаскивания
Контроль за правильностью выполнения заданий осуществляют учащиеся класса и учитель
Для формирования графических навыков учащихся два последних задания выполняются в тетрадях и затем проверяют на доске.
5. Формирование навыков работы с дробными значениями координат
На доске переходим к пятому слайду. Слайд 5.

На слайде посроена координатная прямая с единичным отрезком равным
Учащиеся чертят аналогичную координатную прямую в рабочих тетрадях и отмечают на ней точки в следующем порядке:
отметьте начало отсчёта
отметьте на координатной прямой целые отрезки
отметьте на координатной дробные значения
Все этапы построения последовательно выполняются учащимися в рабочих тетрадях и проверяются на доске.
V . Подведение итогов урока.
После выполнения работы на компьютерах учащиеся занимают свои места.
В слайде 5 переходим по гиперссылке к слайду с целями урока.
Учитель подводит итоги работы учащихся и ставит оценки за работу на уроке.

VI . Домашнее задание.

Координатная прямая
Урок математики в 6 классе

Слайд 1. Постановка образовательных целей урока

Описание слайда 2.
Слайд 3. Используется для формирования навыков определения координат точек

Самопроверка после выполнения задания путём сравнения при открытии закрытого текста
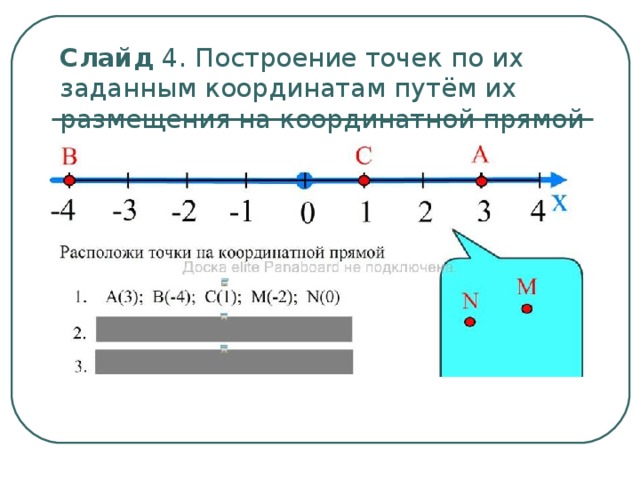
Слайд 4. Построение точек по их заданным координатам путём их размещения на координатной прямой
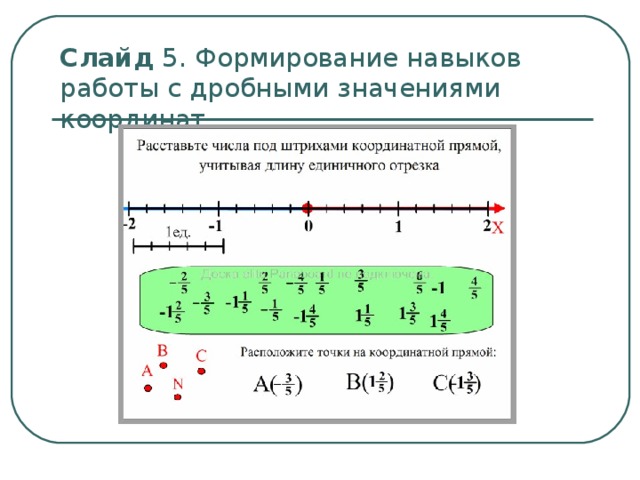
Слайд 5. Формирование навыков работы с дробными значениями координат

В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.
Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.
Положительные и отрицательные числа
Начнем с сухих, но емких определений.
Обычно + не пишется, а просто подразумевается.
Числа 2, \(\mathbf>\), \(\mathbf>\), 9871254 - перед ними не стоит никакой знак, соответственно, эти числа положительные.
Приведем примеры отрицательных чисел:
-3, \(\mathbf>\), \(\mathbf>\), -784285332
Минус уже опустить нельзя, так как тогда получится, что число положительное.
Важные факты:
- Все положительные числа строго больше нуля
- Все отрицательные число строго меньше нуля
- 0 не относится ни к положительным, ни к отрицательным числам
Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.
Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.
Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.
Пройти тест и получить оценку можно после входа или регистрации
Неположительные и неотрицательные числа
Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.
Удобно, что для этого есть специальные определения.
Определение: Неотрицательные числа - это все положительные числа и 0.
Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.
Примеры: 0, 1, 956, \(\mathbf>\), \(\mathbf>\).
Определение: Неположительные числа - это все отрицательные числа и 0.
В данном случае примерами будут соответственно отрицательные числа или 0.
Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:
- Отрицательное число является неположительным
- Положительные число является неотрицательным
- 0 является одновременно и неположительным, и неотрицательным числом
Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:
Пройти тест и получить оценку можно после входа или регистрации
Координатная прямая
Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.
Определение: координатная прямая - это прямая с указанной на ней точкой начала отсчета, направлением и единичным отрезком.

Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.
Выше мы показали самую простую вариацию координатной прямой.
Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.

Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.

Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.

Неизменным на всех этих картинках остается наличие трех пунктов из определения:
- Точка начала отсчета
- Направление
- Единичный отрезок
В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.
Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.
На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.

Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.
На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.
Введем еще одно определение: координата точки - это число, показывающее положение точки на координатной прямой.

На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,
координата- 1.
Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.
Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.
Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.
Этот случай иллюстрирует точка D - она находится на расстоянии полутора единичных отрезков от точки начала отсчета.
Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.
Таким образом, координата точки D будет равна \(\mathbf\).
Представьте, что направление идет в другую сторону.

В таком случае точки справа от точки начала отсчета будут иметь отрицательные координаты, а точки слева точки начал отсчета - положительные.
С целью закрепления изученного материала учащимся можно предложить различные индивидуальные задания: по заданным координатам точек построить фигуру, соединяя последовательно построенные точки. В сборнике представлены задания различного уровня сложности. Тем самым применяется дифференцированный подход в обучении.
Данный материал можно использовать как в урочной, так и внеурочной деятельности.
Данный материал можно использовать по разному. Можно распечатать карточки с заданиями, а ответы не выдавать. Желательно не указывать название рисунка. А можно сформулировать обратное задание: по данным рисунка запишите последовательно координаты точек. А можно использовать этот дидактический материал и по другому: сформулировать обратное задание. Для того, чтобы облегчить проверку такого задания, можно указать с какой точки начать записывать координаты и в каком направлении двигаться от этой точки.
(1; 7), (0; 10), (-1; 11), (-2; 10), (0; 7), (-2; 5), (-7; 3), (-8; 0), (-9; 1), (-9; 0),
(-7; -2), (-2; -2), (-3; -1), (-4; -1), (-1; 3),
(0; -2), (1; -2), (0; 0), (0; 3), (1; 4),
(2; 4), (3; 5), (2; 6), (1; 9), (0, 10);

(3 ; 5), (2; 3), (1; 5), (2; 6), (3; 5), (6; 5), (6; 4), (8; 4), (8; 2), (6; 1), (3; -1), (4; -6), (6; -7), (3; -7), (1; -1,5), (-4; -2), (-5; -5), (-6; -6), (-4; -7), (-8; -7), (-8,5; 0), (-7; 2), (-8; 3), (-7,5; 5), (-6; 6), (-3; 6), (-2; 5), (-2; 4), (-3; 5), (-6; 5), (-6; 3), (1; 2), (2; 3), (6; 1);


(15; 3), (15; 4), (10; 1), (9; 2), (8; 2),
(7; 1), (3; 1), (-4; 0), (-16; -2), (-5; -3),
(-6; -4), (-3; -4), (-2; -3), (-1; -4), (1; -4),
(0; -3), (4; -3), (4; -4), (7; -4), (6; -3),
(8; -4), (10; -4), (8; -3), (15; 0), (10; 0),
(15; 3);


(3; 3), (0; 3), (-2; 2), (-5; 2), (-7; 4),
(-8; 3), (-7; 1), (-8; -1), (-7; -2), (-5; 0),
(-1; -2), (0; -4), (2; -4), (3; -2), (5; -2),
(7; 0), (5; 2), (3; 3), (2; 4), (-3; 4), (-4; 2);

(-5; -10), (-6; -10), (-8; -12), (-8; -14),
(-7; -15), (-4; -15), (-3; -14), (-2; -12),
(0; -5), (1; 0), (2; 3), (3; 2), (4; -3), (6; 0),
(8; -4), (8; -8), (10; -4), (11; 1), (11; 5),
(9; 8), (5; 11), (6; 13), (5; 11), (-1; 12),
(-8; 9), (-9; 7), (-10; 2), (-6; 5), (-4; 4),
(-3; 1), (-1; 3), (2; 3).

(0; 7), (4; 8), (6; 7), (8; 6), (7; 7),
(6; 9), (5; 11), (5; 12), (6; 11), (7; 12),
(7; 10), (10; 7), (10; 5), (8; 3), (6; 3),
(7; 2), (9; 2), (9; 1), (8; 1), (7; 0), (6; 0), (7; -2), (8; -3), (8; -4), (10; -7,5), (9; -8), (7,5; -8), (7; -6), (5; -5), (6; -7), (4,5; -8), (4; -9), (2; -7), (3; -6), (2; -5), (1; -5,5), (0; -7), (0; -9), (-2; -10), (-3; -9,5), (-3,5; -8), (-5; -10), (-6,5; -9), (-7; -7), (-6; -7), (-5; -5), (-6; -3), (-8; -4), (-6; 0), (-4; 1), (-3; 3), (-3; 5), (-4,5; 6), (-5; 7,5),
(-3; 7,5), (-2; 7), (-2; 8), (0; 7);

(1,5; 0,5), (3; 0), (3,5; 0), (8; 0,5),
(7,5; 4,5), (9; 3), (12; 1,5), (18; 1,5), (12,5; 3), (11; 3,5), (9,5; 7), (8; 10),
(6; 11), (4; 12,5), (3; 14), (2; 16),
(2,5; 17,5), (2; 18), (1; 16,5), (0,5; 18), (0; 16), (-0,5; 15,5), (-2; 14,5), (-1,5; 14), (-1; 14,5), (-1; 14), (0; 14), (0,5; 13,5), (1,5; 10,5), (0,5; 8), (1; 7), (1; 6), (1,5; 6), (1,5; 7,5), (2,5; 10,5), (2; 7,5), (2,5; 6,5), (3; 6,5), (2,5; 8), (3; 8,5), (3,5; 6,5),
(3; 6), (4; 4,5), (4; 3), (0; 3), (0,5; 2),
(5,5; 2), (5,5; 4), (6,5; 4), (6,5; 1),
(1,5; 0,5), (3; 0);

(-7,5; 4,5), (-8; 5), (-10,5; 3,5),
(-10; 3), (-7; 4,5), (-5; 5,5), (-5,5; 8), (-5; 8), (-4,5; 6), (-4; 6), (-2; 2), (0; 1), (4,5; 0), (7; 4), (8; 4), (5,5; 0), (6; -5),
(4,5; -6), (4; -5), (4,5; -4,5), (4; -4), (3; -6), (1,5; -6), (1,5; -5,5), (2,5; -5),
(2,5; -4,5), (3,5; -3,5), (2,5; -4,5), (2; -5), (2; -4), (1; -5), (1; -4,5), (0; -5), (-1; -4,5),
(-2; -4,5), (-2,5; -6), (-4; -5), (-2,5; -3,5), (-3; -2,5), (-3,5; -4), (-4; 1), (-4,5; 0,5),
(-4,5; 1), (-5,5; 0), (-6; 0,5), (-6,5; -1),
(-8; 0), (-9; -1), (-10; 3);


(-8; 0), (-7; -4), (-4; -7), (4; -7),
(7; -4), (8; 0), (7; 4), (9; 7), (9; 10),
(4,5; 10,5), (1,5; 7,54), (0; 8), (-1,5; 7,5), (-4,5; 10,5), (-9; 10), (-9; 7), (-7; 4),
(-8; 0);
(1; 3), (3; 5), (5; 3), (3; 4), (1; 3).

(2,5; 2), (1,5; 3), (1,5; 4), (3; 5),
(3,5; 5,5), (5,5; 9), (6; 9,5), (6,5; 9,5), (6,5; 7), (5,5; 3,5), (4,5; 2), (2,5; 2),
(-3; 0), (-6; -2,5), (-7; -5), (-7; -7,5),
(-8; -7), (-9; -6), (-9; -3), (-7; -1), (-6; -1), (-5,5; -1,5), (-5; -1), (-5,5; 0), (-8; 0),
(-10; 2), (-11; -4), (-11; -6); (-10; -8),
(-8; -9), (-6,5; -9), (-7; -10,5), (-6; -11), (1,5; -11), (1,5; -10,5), (0,5; -9,5),
(-1; -9,5), (0; -8), (4; -6), (5; -10),
(6; -11), (8; -11), (8; -10,5), (7,5; -10), (6,5; -10), (6,5; -7), (7; -4,5), (9; -2),
(9,5; 0), (9; 2), (8; 4), (8; 5), (13; 7,5), (12; 7,5), (12,5; 8), (13; 9), (13; 10,5), (12,5; 10,5), (12; 10), (10; 10), (9; 11), (7; 12), (6; 12), (3,5; 10), (3; 9), (3; 7), (3,5; 5,5);
(7; -4,5), (11; -2,5), (13; -2,5),
(14; -3), (15,5; -3), (15,5; -2,5), (15; -2,5), (13; -1), (9,5; 0);

(-4; 5), (-3; 2), (0; 0), (1; 2), (2; 1), (3; 1), (5; -1), (4; -2), (2; -2), (2; -3), (4; -3),
(2; -9), (0; -7), (1; -5), (1; -4), (0; -4),
(0; -9), (-3; -9), (-3; -3), (-8; -3), (-7; -7), (-8; -7), (-8; -8), (-11; -8), (-10; -4),
(-11; -1), (-14; -3), (-12; -1), (-11; 2),
(-8; 4), (-4; 5), (0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; -2),
(5; -3), (4; -3);

(1; -2), (3; 4), (6; 5), (9; 2), (9; 0),
(8; -4), (5; -1), (4; -1), (1; -4), (1; -6), (-4; -6), (-3; -5), (-1; -5), (-3; -4), (-3; -3), (-1; -1), (-1; 0), (-3; 0), (-3; -1), (-4; -1), (-4; 0), (-3; 1), (-1; 1), (-1; 2), (-3; 3), (-1; 4),
(0; 6), (1; 4), (1; -2);

(4; 2), (4; -3), (2; -3), (2; -4), (1; -5), (3; -5), (3; -7), (2; -7), (2; -6), (1; -6),
(1; -5), (-2; -5), (-2; -7), (-4; -7), (-4; -6), (-3; -6), (-3; -4), (-2; -4), (-2; -1), (-3; -2), (-3; 0), (-2; 0), (-2; 2), (-3; 2), (-5; 3),
(-3; 4), (-2; 5), (-2; 6), (0; 8), (1; 8),
(2; 7), (2; 5), (1; 4), (1; 2), (2; -2), (2; -3);

(-1; 2), (-2; 3), (-2; 4), (0; 5), (2; 4), (2; 3), (1; 2), (-1; 2);
(4; -4), (5; -3), (6; -3), (7; -4), (7; -5), (6; -6), (5; -6), (6; -5), (5; -4), (4; -4).


(-7; 0), (-5; 2), (7; 2), (9; 5), (10; 5), (10; 1), (9; 0), (-7; 0);

(-8; 1), (-6; 2), (-2; 0), (1; 2), (5; 1), (7; -4), (9; -3);
(-2; 6), (0; 8), (3; 7), (5; 5), (7; 7);
(1; 2), (3; 7), (3; 9), (3; 10), (4; 11), (5; 11), (6; 10), (6; 9), (5; 8), (4; 8),
(3; 9).

(-7; 0), (-3; 9), (-1; 11), (1; 11), (3; 9), (7; 0), (5; 0), (1; 3), (-1; 3), (-5; 0),
(-7; 0);
(1; -9), (2; -8), (2; 1), (1; 3), (-1; 3), (-2; 1), (-2; -8), (-1; -9), (1; -9);
(3; 2), (3; 3), (4; 3), (4; 2), (3; 2);
(0; 8), (0; 9), (1; 9), (1; 8), (0; 8);
(0; 4), (0; 5), (1; 5), (1; 4), (0; 4).

(1; 5), (0; 6), (-1; 5), (0; 4), (1; 5);

(-7; -2), (-3; 4), (-1; 4), (2; 7), (2; 4), (5; 4), (9; -5), (10; -9), (8; -8), (5; -10), (7; -5), (3; -2), (-7; -2);
Читайте также:


