Как сделать конус с вырезом
Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).
1. Полный конус
Параметры выкройки рассчитываются по формулам:
" />
;
;
где " />
.
2. Усеченный конус
Формулы для вычисления параметров выкройки:
" />
;
" />
;
;
где )^2>" />
.
Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .
3. Угол при вершине конуса
Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.
4. Методы построения выкройки
- Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
- Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
- использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.
5. Не параллельные основания
Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания.
Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:
Усеченный конус с не параллельными основаниями.
Калькулятор рассчитывает развертку (выкройку) на плоскости прямого кругового конуса и усеченного прямого кругового конуса.
Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости. Картинка ниже иллюстрирует задачу.
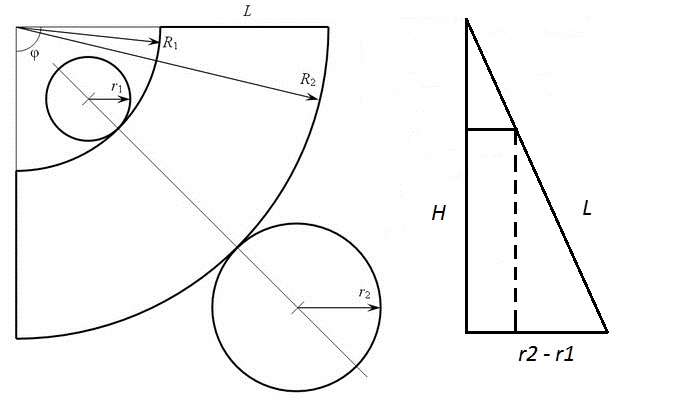
Про конус нам известен радиус основания и высота конуса (или высота усеченного конуса). Для описания развертки нам надо найти радиус внешней дуги, радиус внутренней дуги (если конус усеченный), длину образующей и центральный угол.
Длину образующей можно посчитать по теореме Пифагора:
,
при этом для полного конуса r1 просто обращается в ноль.
Радиус внутренней дуги можно найти из подобия треугольников:
,
опять же, для полного конуса она равна нулю.
Соответственно, радиус внешней дуги:
,
для полного конуса он совпадает с L.
Компас 3д заточен под осуществление твердотельного моделирования. В нем без особых проблем можно создать детали и изделия практически любой сложности. Как говорится, легче один раз увидеть на примере, чем сто раз услышать, поэтому в текущей статье наглядно разберем создание 3д модели в Компасе на примере примитивов: цилиндра и конуса.
Благодаря дружелюбному интерфейсу Компаса, во время работы присутствует фактор вариативности. Иными словами, одну и ту же операцию можно выполнить разными способами с одинаковым успехом. Поэтому в данной статье будет представлен наиболее классический способ построения примитивов.
Как сделать цилиндр в 3д Компасе ?
Самый первый примитив для построения — цилиндр. При его построении научимся создавать эскизы и пользоваться инструментом выдавливания для создания тела.
Создание эскиза цилиндра в Компасе
При создании новой 3д модели в Компасе перед лицом пользователя возникает пустой экран с сеткой координатных осей и базисных плоскостей (рис. 1) с началом в точке с нулевыми координатами. Относительно нуля рекомендуется создавать детали, располагая их так, чтобы какая-либо из базисных осей была осью симметрии. Возьмем во внимание пару фактов:
- Принято, что по оси Z (синяя) закладываются размеры высот, поэтому вдоль нее будет вытянут будущий цилиндр.
- В плоскости XoY (синяя) обычно закладывается базовая кромка разрабатываемой детали. Именно в этой плоскости будет создан эскиз основания цилиндра (окружность).
После вышеописанных манипуляций получилась окружность с центром в нулевой координате, лежащей в горизонтальной плоскости XoY (рис. 4). Чтобы выйти из режима эскиза, нужно нажать на зеленую кнопку справа вверху экрана.
Создание поверхности цилиндра в Компасе
Таким образом получилось создать 3д модель цилиндра в Компасе.
Как построить конус в Компасе 3D?
У конуса ось вращения проходит от вершины к центру окружности-основания, соответственно эти две точки будут располагаться на оси Z, причем основание с центром в нулевой координате и в плоскости XoY.
Таким образом, в текущей статье были рассмотрено создание 3д модели в Компасе на примере построения таких примитивов как цилиндр и конус с использованием эскизов для построения и инструментов выдавливания, выреза выдавливанием, вращения. Это базовые приемы для создания простейших моделей в Компасе.
В этот раз хочется повести речь, о чуть более сложных моделях, и их изображении на чертежах. В качестве примера рассмотрим сквозное отверстие в призматической фигуре, и подробно распишем последовательность построение этого отверстия в трех основных проекциях.
Первое, с чего стоит начинать чертеж модели – это конечно построение осевой линии. Это вертикальная или горизонтальная штрихпунктирная линия, идущая вдоль оси тела, которая в нашем случае является осью симметрии. Затем приступаем к построению контура фигуры и первым делом рисуем главный вид (рисунок 1) с которого в дальнейшем нарисуем два других вида модели. Для того, чтобы правильно вычертить отверстие на трех проекциях, используют проекционные связи. Т.е. если у вас есть отверстие на одном из видов, например, на главном, зная несколько простых правил, вы сможете вычертить это отверстие и на других двух видах.

Рисунок 1. Главный вид правильной четырехугольной пирамиды с цилиндрическим отверстием

Рисунок 2. 3D модель правильной четырехугольной пирамиды с цилиндрическим отверстием
Из трех основных точек (1 и 3 лежат на ребре пирамиды и 2 на оси окружности) проведем прямые (рисунок 3), параллельные основанию пирамиды (тонкие зеленые линии). Через полученные на боковом ребре точки откладываем вертикальные линии (толстые зеленые линии). На горизонтальной плоскости проводим вспомогательные (красные линии), параллельные ребру у основания пирамиды. Проецируем точки 1, 2 и 3 с окружности на горизонтальную плоскость (синие линии). Места пересечений (красных и синих линий) и будут точками проецируемого отверстия (1',2' и 3'). Отмечаем несколько произвольных точек на контуре отверстия (рисунок 4), и повторяем действия, совершенные выше. Следует учитывать, что чем больше точек отверстия вы перенесете на горизонтальную плоскость, тем точнее будет контур кривой.

Рисунок 3. Перенос основных точек окружности с фронтальной проекции на горизонтальную

Рисунок 4. Проецирование вспомогательных точек (аналогично основным)
Строим искомую кривую по точкам (рисунок 5). Симметрично достраиваем всю проекцию (рисунок 6).

Рисунок 5. Построение искомой кривой по точкам

Рисунок 6. Отображение всего отверстия на горизонтальной плоскости
Для построения отверстия на профильном виде используем те же проекционные связи. Причем длины отрезков (зеленые толстые линии) будут равны отрезкам на горизонтальной проекции (Рисунки 7 и 8).

Рисунок 7. Нахождение точек пересечения отверстия и пирамиды на профильной проекции

Рисунок 8. Построение кривой на профильной плоскости (красная толстая линия)
Теперь осталось по полученным точкам построить кривые и удалить вспомогательные линии, чертеж фигуры готов (рисунок 9).

Рисунок 9. Отображение трех проекций геометрического тела с отверстием
Примеры проецирования еще некоторых геометрических фигур: конус с призматическим отверстием (рисунок 10) и шар с цилиндрическим отверстием (рисунок 11).

Наш онлайн калькулятор имеет встроенные формулы, что позволяет производить расчет данных показателей, просто выбрав вид конуса и введя абсолютные значения в соответствующие ячейки. Возможности и принцип построения системы калькулятора исключают допущение ошибок при расчетах, и избавляют пользователя от необходимости в самостоятельном детальном изучении методик расчета.
Преимущества, которые дает онлайн калькулятор
- Большая экономия времени;
- Гарантированно правильный и предельно точный расчет;
- Удобный интерфейс, который будет понятен даже новичку;
- Открытый доступ к калькулятору для всех пользователей.
Таким образом, можно сделать вывод, что расчет развертки конуса требует концентрации внимания на многих деталях, и самостоятельный его расчет является достаточно трудоемким. Наш онлайн калькулятор является инструментом, который упростит Вашу жизнь при точном расчете данного показателя. Также Вам доступна информация о том, какая формула применяется при расчете и определенная справочная информация.
Читайте также:


