Как сделать конус из ткани
В основном новогодний декор не так уж и сложен: побольше блесток, гирлянд, свечей, все красное и зеленое. И поэтому сделать своими руками новогодний декор достаточно просто. Главное найти идею!
В наше время в интернете можно найти все, было бы время.
У меня много разных идей собрано в копилочке и я теперь я делюсь с вами. Заодно немного порассуждаю как и из чего можно сделать такой декор.
Все фотографии взяты из открытых источников.
Очень простая ёлочка из ниток, которую можно сделать даже с детьми.
- Нужна рамочка (не обязательно такая заляпанная)
- Нитки зеленые, для бантика можно и красную и для ствола шпагат
Еще вариант текстильных ёлочек.
Конус можно купить готовый из пенопласта, а можно и просто свернуть из плотной бумаги и внутрь для укрепления что-нибудь натолкать, хоть мятой газеты.
Понравившиеся вам ткани нарезать на полоски в два раза больше чем нужны, свернуть пополам и накрутить на конус вниз сгибом внахлест на предыдущий слой, чтобы закрыть не обработанный край.
Сверху готовую звезду, можно большую бусину, да хоть из мишуры свернуть шарик
И еще вариант елочек из ткани.
- конусы
- ткань
- клей ПВА или заваренный крахмал
Мне кажется они сделаны из готовых ленточек. По виду они плотные, можно их смочить в разбавленной воде с ПВА 50/50 или заваренный крахмал.
Ствол можно сделать из пробки от шампанского, а можно и вообще без ствола сделать
Добавим немного гламура.
Те же конусы из бумаги. Покрыть клеем и обильно обсыпать блестками. На клей же добавить еще декора

Наш онлайн калькулятор имеет встроенные формулы, что позволяет производить расчет данных показателей, просто выбрав вид конуса и введя абсолютные значения в соответствующие ячейки. Возможности и принцип построения системы калькулятора исключают допущение ошибок при расчетах, и избавляют пользователя от необходимости в самостоятельном детальном изучении методик расчета.
Преимущества, которые дает онлайн калькулятор
- Большая экономия времени;
- Гарантированно правильный и предельно точный расчет;
- Удобный интерфейс, который будет понятен даже новичку;
- Открытый доступ к калькулятору для всех пользователей.
Таким образом, можно сделать вывод, что расчет развертки конуса требует концентрации внимания на многих деталях, и самостоятельный его расчет является достаточно трудоемким. Наш онлайн калькулятор является инструментом, который упростит Вашу жизнь при точном расчете данного показателя. Также Вам доступна информация о том, какая формула применяется при расчете и определенная справочная информация.


Булычева Марина. Papercraft Макеты Шаблоны. запись закреплена
ПОДЕЛЮСЬ СВОЕЙ АВТОРСКОЙ ВЫКРОЙКОЙ КОНУСА
(плайм-пакет) для свит-композиций!


Спасибо большое за Ваше творчество. Очень полезная штука



Наталья Дринько



Светлана Янышевская
Спасибо, Марина. Ты не перестаёшь удивлять и своими талантами и тем, как ты продвигаешь свое творчество. Каждый раз что-то новое



Анастасия Лощилова


Спасибо


Наталья Гусева
Благодарю! Эти конусы сейчас очень популярны)


Большое спасибо




Анна Колосова


Спасибо


Огромное спасибо

Катюша Стасевич


Спасибо


Спасибо за идею


Ульяна Киреева

Марина, вы просто молодец! Правильно говорят талантливый человек талантлив во всем


Марина, большое СПАСИБО за выкройку плайм-пакета и выкройку для пеноплекса. В преддверии 1 сентября очень актуально.


Галина Рощупкина




Спасибо большое!


Спасибо большое.

Спасибо! Правда, после суточного перелета с вниманием плохо, но я старалась

Я в городе обыскалась уже такие стаканчики для композиций на 1 сентября)) оптом брать на хотелось и тут на удачу, вы безумно выручаете!! Спасибо огромное!!


Огромное спасибо!




Спасибо большое, круто

Огромное спасибо! Это здорово.


Ульяна Киреева

Спасибо


Александра Юдина

Спасибо




Екатерина Новикова
Спасибо Очень классная штука. Правда цветы делать не умею, зато другая идейка появилась чем заполнить)
Калькулятор рассчитывает развертку (выкройку) на плоскости прямого кругового конуса и усеченного прямого кругового конуса.
Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости. Картинка ниже иллюстрирует задачу.
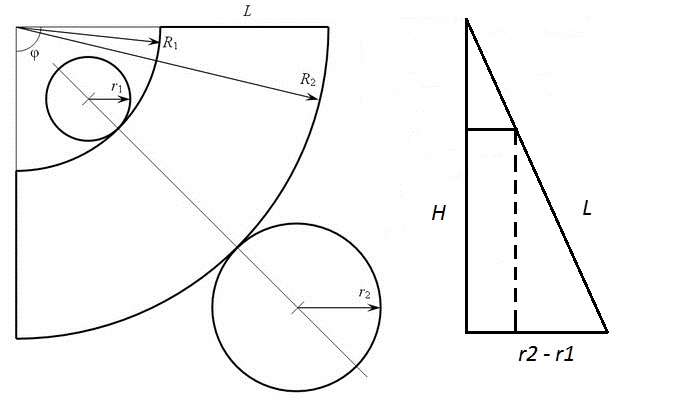
Про конус нам известен радиус основания и высота конуса (или высота усеченного конуса). Для описания развертки нам надо найти радиус внешней дуги, радиус внутренней дуги (если конус усеченный), длину образующей и центральный угол.
Длину образующей можно посчитать по теореме Пифагора:
,
при этом для полного конуса r1 просто обращается в ноль.
Радиус внутренней дуги можно найти из подобия треугольников:
,
опять же, для полного конуса она равна нулю.
Соответственно, радиус внешней дуги:
,
для полного конуса он совпадает с L.
Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки.
Иногда возникает задача – изготовить защитный зонт для вытяжной или печной трубы, вытяжной дефлектор для вентиляции и т.п. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами.
Начнем с простого варианта — развертка простого конуса. Проще всего объяснить принцип расчета выкройки на примере.

Допустим, нам надо изготовить конус диаметром D см и высотой H сантиметров. Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. Известны два параметра – диаметр и высота. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). Половина диаметра (радиус) и высота образуют прямоугольный треугольник. Поэтому:

Итак, теперь мы знаем радиус заготовки и можем вырезать круг.
Вычислим угол сектора, который надо вырезать из круга. Рассуждаем следующим образом: Диаметр заготовки равен 2R, значит, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам нужно вырезать сегмент с длиной дуги равной разности этих длин. Применим правило соотношения. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.

Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим путем вычитания 360 – Х.
Из круглой заготовки с радиусом R надо вырезать сектор с углом (360-Х). Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера.
Например: Нам нужен конус для зонта вытяжной трубы высотой (Н) 100 мм и диаметром (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности нужного нам конуса — 250 x 3,14 = 785 мм.
Читать еще: Красивые новогодние гирлянды. Как сделать новогодние гирлянды своими руками из бумаги. Флажки из бумаги тишью
Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать надо сектор 360 – 281 = 79 градусов.

Расчет заготовки выкройки для усеченного конуса.
Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции.
Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.

В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения.
Отсюда Р = D x H / (D-Dm).

Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2.
Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2.
Теперь осталось рассчитать угол сектора, который надо вырезать.
Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов.
Т.е. Х / 360 = 3,14 x D / 6.28 x Rz
Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.

Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм.
Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм
По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)^2 + 6002 = 618,5 мм
По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)^2 + (200/2)^2 = 364 мм.
Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса.
На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест.
Константин Тимошенко © 31.07.2014 г.
Как вы решили этот пример? 300 х 250 / (300 – 200) = 600 мм
Калькуляторы расчета размеров развертки конуса
Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса
Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.
Калькуляторы расчета размеров развертки конуса
Несколько слов о рассчитываемых параметрах
Понять принцип расчета будет несложно, разобравшись со следующей схемой:
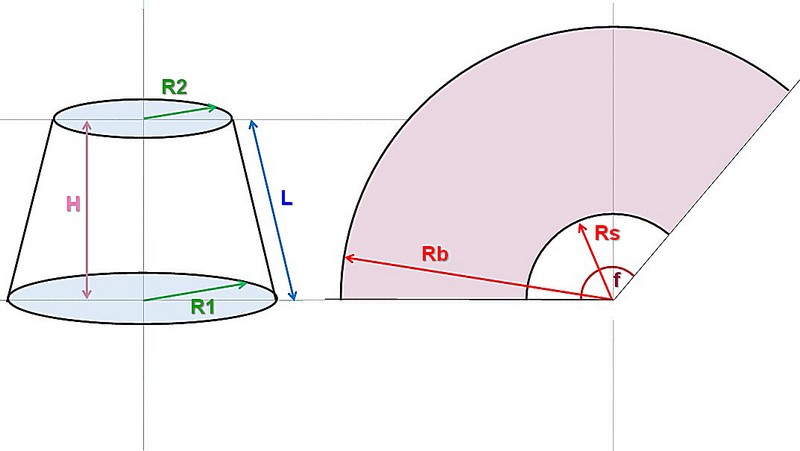
Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.
Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.
Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.
Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L
Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.
Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:
Шаг 1 – определение длины образующей L
(Если она уже известна – шаг пропускается)
Шаг 2 – определение радиусов внутренней и внешней дуги развертки
Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.
Построение развертки конуса
Развертка поверхности конуса — это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.
Варианты построения развертки:
Развертка прямого кругового конуса
Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.
Читать еще: Крайне полезные вязанные мочалки. Вязание крючком.Красивые детские и взрослые мочалки своими руками.Видео

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.
- Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
- Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.
На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S A B . Длины его сторон S A и S B равны образующей l конической поверхности. Величина A B соответствует длине A’B’. Для построения треугольника S A B в произвольном месте чертежа откладываем отрезок S A =l, после чего из точек S и A проводим окружности радиусом S B =l и A B = A’B’ соответственно. Соединяем точку пересечения окружностей B с точками A и S .
Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.
Развертка наклонного конуса
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

- Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
- Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5. - Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S 1 6 , S 6 5 , S 5 4 , S 4 3 , S 3 2 , S 2 1 . Построение каждого треугольника выполняется по трем сторонам. Например, у △S 1 6 длина S 1 =S’’1’’ , S 6 =S’’6’’1, 1 6 =1’6’.
Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.
Перенос линии с поверхности конуса на развертку
Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

- Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
- Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
- Находим положение точек A , B , C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S A =S’’A’’, S B =S’’B’’1, S C =S’’C’’1.
- Соединяем точки A , B , C плавной линией.
Развертка усеченного конуса
Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.
Читайте также:


