Как сделать комбинаторику
Комбинаторика – раздел математики, занимающийся изучением количества возможных комбинаций определенного типа, которые возможно сделать из некоторого набора элементов. Эти вычисления необходимы для решения различных задач в теории вероятностей и получения распределений случайных величин.
Правила в комбинаторике
Правило суммы: если есть взаимоисключающие друг друга действия A и B, которые можно выполнить способами m и n соответственно, то выполнить любое из этих действий можно m + n способами.
Правило произведения: если есть последовательность действий k, и первое действие его можно выполнить n1 способом, второе n2 и далее до nk, то все действия этой последовательности можно выполнить n1 · n2 · nk способами.
Элементы комбинаторики
Размещения из n по k – упорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Для расчета способов размещения следует воспользоваться формулой: P k n = n! / (n - k)!
Перестановки – конечное множество, в котором указан порядок его элементов. Количество перестановок вычисляется по формуле: Pn = n!
Сочетания из n по k – неупорядоченное множество, состоящее из k элементов, которые выбраны из n элементов. Число сочетаний из n элементов по k рассчитывается так: n! / (n - k)! · k!
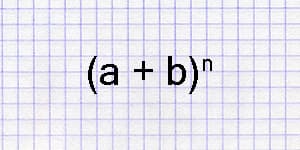
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
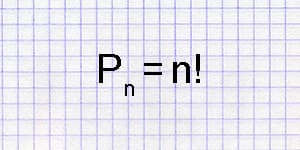
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
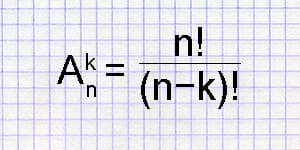
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
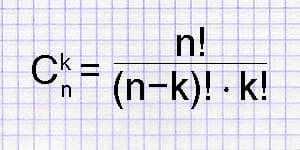
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.

Рассмотрим множество, состоящее из n различных элементов. Требуется выбрать из них какие-нибудь k элементов и расположить эти k элементов в каком-либо порядке. Такие упорядоченные последовательности называются размещениями из n элементов по k элементов (упорядоченные – следовательно, последовательности и — различные размещения).
Если в последовательности нет одинаковых элементов, то говорят о размещении без повторений. Их количество
Если в последовательности допускается наличие одинаковых элементов, то говорят о размещении с повторениями. Их количество
Любое подмножество (неупорядоченное), состоящее из k элементов, называется сочетанием из n элементов по k элементов.
Различные сочетания отличаются друг от друга только самими входящими в них элементами, порядок их следования безразличен, т.е. по условию задачи подмножества и не различны (соединены).
Число сочетаний без повторений
Число сочетаний с повторениями
Количество способов переставить элементов в заданном множестве (количество перестановок) вычисляется по формуле
При решении простейших комбинаторных задач можно использовать следующую таблицу, определяющую число множеств, состоящих из k элементов, отбираемых из множества, содержащего n элементов
| Выбор | Неупорядоченный | Упорядоченный |
| Без повтора | ||
| С повтором |
Рассмотрим разницу между сочетаниями, размещениями с повторениями, без повторений на следующих примерах.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.1 В коробке 6 шаров, пронумерованных от 1 до 6. Из коробки вынимаются друг за другом 3 шара и в этом же порядке записывают полученные цифры. Сколько трехзначных чисел можно таким образом записать?
Решение: По условию задачи подмножества и – различные. Повторов в подмножестве быть не может, так как шары не возвращаются в коробку.
ПРИМЕР 13.2.2. В коробке 6 шаров пронумерованных от 1 до 6. Из коробки вынимаются 3 шара и записывают число в порядке возрастания цифр. Сколько трехзначных чисел можно таким образом записать?
Решение: По условию задачи подмножества и дают число 123, т.е. не являются различными.
ПРИМЕР 13.2.3. Условие задачи 2.1 (шары возвращаются в коробку)
ПРИМЕР 13.2.4. Условие задачи 2.2 (шары возвращаются в коробку)
ПРИМЕР 13.2.7. В мастерской имеется материал 5 цветов. Поступил заказ на пошив флагов, состоящих из трех горизонтальных полос разного цвета каждый. Сколько таких различных флагов может сшить мастерская?
Решение: Флаги отличаются друг от друга как цветом полос, так и их порядком, поэтому разных флагов можно сделать штук.
ПРИМЕР 13.2.8. Сколькими способами можно распределить 5 учеников по 3 параллельным классам?
Решение: Составим вспомогательную таблицу
Таким образом, видно, что если для одного ученика существует 3 варианта выбора класса, то для всех 5 учеников существует способов распределения по классам.
ПРИМЕР 13.2.9. На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй том не стояли рядом?
Решение: Произведем рассуждения “от обратного”. Тридцать томов на одной полке можно разместить 30! способами.
Если 1 и 2 тома должны стоять рядом, то число вариантов расстановки сокращается до , т.к. комбинацию из 1 и 2 тома можно считать за один том, но при этом они могут стоять как (1;2) или (2;1), т.е.
Тогда искомое число способов расстановки есть
ПРИМЕР 13.2.10. Чемпионат, в котором участвуют 16 команд, проводится в два круга, т.е. каждая команда дважды встречается с любой другой. Определить, какое количество встреч следует провести.
Решение: По условию задачи из 16 команд для каждой встречи требуется отобрать 2 команды. В данном случае отбор производится без повтора и порядок отбора не важен, т.е. число вариантов — . Так как команды должны играть дважды число вариантов удваивается, т.е. .
ПРИМЕР 13.2.11. Автомобильная мастерская имеет для окраски 10 основных цветов. Сколькими способами можно окрасить автомобиль, если смешивать от 3 до 7 основных цветов?
Решение: По условию задачи отбор цветов для окраски производится без повтора и порядок отбора не важен, т.е. число вариантов зависит лишь от числа отбираемых для окраски цветов — . Поэтому общее число вариантов есть
ПРИМЕР 13.2.12. Турист прошел маршрут из пункта A в пункт B, из B в C и вернулся обратно. Сколько вариантов маршрута существует, если из пункта A в пункт B ведут 3 дороги, а из B в C — 4 и нельзя возвращаться той дорогой, по которой уже прошел?
Решение: Составим схему.
Из рисунка видно, что вариантов маршрута из А в B существует 3, и из B в C – 4, т.е. всего маршрутов .
На обратном пути вариантов маршрута из С в B существует 3 (один уже пройден), и из B в А – 2, т.е. всего возможных обратных маршрутов осталось . Тогда всего вариантов маршрута .
ПРИМЕР 13.2.13. Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда по 6 человек, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
Решение: Рассуждения произведем несколькими способами
I способ) Первоначально 12 учеников разбивают на 2 группы по 6 человек. Это можно сделать способами.
Затем они могут распределиться по своим рядам согласно схеме
Поэтому всего способов распределения учеников будет .
II способ) Первоначально 12 учеников запускают в класс, указывая место, где каждый должен сидеть, например “второй ряд, третье место”. Так как посадочных мест также 12, то всего вариантов распределения 12!
Варианты контрольной работы могут распределиться
“I вариант – I ряд, II вариант – II ряд”
“II вариант – I ряд, I вариант – II ряд”,
Таким образом, всего способов распределения учеников будет .
По приведенным решениям видно, что результаты решений совпадают.
ПРИМЕР 13.2.14. Сколько существует вариантов расположения шести гостей за круглым шестиместным столом?
Решение: Эта задача имеет разные решения и, соответственно разные ответы – в зависимости от того, что понимать под различным расположением гостей за столом. Поэтому исследуем возможные варианты.
Если считать, что нам важно, кто сидит на каком стуле, то это простая задача на перестановки и, следовательно, всего вариантов .
Если же важно не то, кто какой стул занял, а то, кто рядом с кем сидит, то требуется рассмотреть варианты взаимного расположения гостей. В таком случае, расположения гостей, получаемые одно из другого при повороте гостей вокруг стола, фактически являются одинаковыми (смотри рисунок).
Очевидно, что для любого расположения гостей таких одинаковых вариантов, получаемых друг из друга поворотом, — шесть. Тогда общее число вариантов уменьшается в шесть раз и их остается .
В случае же, когда нас интересует только взаимное расположение гостей, то одинаковыми можно считать и такие симметричные расположения, при которых у каждого гостя остаются те же соседи за столом, только левый и правый меняются местами (смотри рисунок).
В такой постановке вопроса общее число различных вариантов расположений гостей уменьшается вдвое и составляет 60.
Отметим, что каждое решение будет считаться правильным при соответствующей постановке задачи.
ПРИМЕР 13.2.15. Семнадцать студентов сдали экзамены по 4 предметам только на “хорошо” и “отлично”. Верно ли утверждение, что хотя бы у двух из них оценки по экзаменационным предметам совпадают?
Решение: Очевидно, что в данном случае речь идет о возможных вариантах вида
| Предмет | 1 | 2 | 3 | 4 |
| Студент 1 | 4 | 4 | 5 | 5 |
| Студент 2 | 5 | 4 | 4 | 5 |
| Студент 3 | 5 | 5 | 5 | 5 |
| … | … | … | … | … |
| Студент 17 | 4 | 4 | 5 | 4 |
Данный пример можно решить способом, изложенным в примере 13.1.8., и получить количество вариантов . Приведем другой наглядный способ решения, использующий так называемое “дерево решений”,который представляет все варианты (16 штук) получения экзаменационных оценок.
По “дереву решений” видно, что 16 студентов могут сдать экзамены только на “хорошо” и “отлично” так, что их результаты будут отличаться, но если студентов 17, хотя бы одно повторение обязательно будет.
При решении задач комбинаторики используются следующие правила.
Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект B может быть выбран nспособами, то:
Правило суммы: выбрать либо A, либо B можно m+n способами.
Правило произведения. Пара объектов (A,B) в указанном порядке может быть выбрана способами.
Примеры и задачи для самостоятельного решения
Решить комбинаторную задачу.
13.2.1.1. В группе 25 студентов. Сколькими способами можно выбрать старосту, заместителя старосты и профорга?
13.2.1.2. В группе 25 студентов. Сколькими способами можно выбрать актив группы, состоящий из старосты, заместителя старосты и профорга?
13.2.1.3. Сколькими способами можно составить список из 10 человек?
Отв.: 3628800
13.2.1.4. Сколькими способами из 15 рабочих можно создать бригады по 5 человек в каждой?
Отв.: 126126
13.2.1.5. Буквы азбуки Морзе образуются как последовательности точек и тире. Сколько букв можно составить, используя для кодировки каждой из букв: а) ровно 5 символов? б) не более пяти символов?
Отв.: а)32; б) 62
13.2.1.6. Кости для игры в домино метятся двумя цифрами. Кости симметричны, и поэтому порядок чисел не существенен. Сколько различных костей можно образовать, используя числа 0,1,2,3,4,5,6?
13.2.1.7. Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти различных звуков?
Отв.: 9864000
13.2.1.8. В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
13.2.1.9. В некоторых странах номера трамвайных маршрутов обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?
13.2.1.10. Команда компьютера записывается в виде набора из восьми цифровых знаков – нулей и единиц. Каково максимальное количество различных команд?
13.2.1.11. Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы 1 и 2 находились бы в соседних аудиториях?
Отв.: 725760
13.2.1.12. Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
13.2.1.13. Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?
13.2.1.14. Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?
Отв.: 9000000
13.2.1.15. У одного студента есть 7 DVD дисков, а у другого – 9 дисков. Сколькими способами они могут обменять 3 диска одного на 3 диска другого?
Отв.: 105840
13.2.1.16. На вершину горы ведут 7 дорог. Сколькими способами турист может два раза подняться на гору и спуститься с нее, если по одной и той же дороге нельзя проходить дважды?
13.2.1.17. У ювелира было 9 разных драгоценных камней: сапфир, рубин, топаз и т.д. Ювелир планировал изготовить браслет для часов, однако три камня было украдено. Насколько меньше вариантов браслета он может изготовить по сравнению с первоначальными планами?
Отв.: 362160
13.2.1.18. В поезд метро на начальной станции вошли 10 пассажиров. Сколькими способами могут выйти все пассажиры на последующих 6 станциях?
Отв.: 60466176
13.2.1.19. За одним столом надо рассадить 5 мальчиков и 5 девочек так, чтобы не было двух рядом сидящих мальчиков и двух рядом сидящих девочек. Сколькими способами это можно сделать?
13.2.1.20. В классе 25 учеников. Верно ли утверждение, что, по крайней мере, у трех из них день рождения в один и тот же месяц?
13.2.1.21. На участке железной дороги расположено 25 станций с билетной кассой в каждой. Касса каждой станции продает билеты до любой другой станции, притом в обоих направлениях. Сколько различных вариантов билетов можно выдать на этом участке?
13.2.1.22. На официальном приеме 50 человек обменялись рукопожатиями. Сколько было сделано рукопожатий?
13.2.1.23. Сколько диагоналей у выпуклого двадцатиугольника?
Часто в жизни возникает потребность определить количество возможных вариантов развития событий. Существует специальная математическая дисциплина, посвященная подобным вопросам. Она называется комбинаторикой.
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Комбинаторика и ее основные принципы
Очевидно, что если в конечном множестве содержится n элементов, то есть ровно n способов выбрать один из них.
Пример. В классе 15 человек. Сколькими способами учитель может назначить одного из них ответственным за чистоту доски?
Ответ. Таких способов ровно 15.
В комбинаторике существует два основных правила. Первое из них называется правилом сложения.
Несмотря на формулировку, по сути это очень простое правило.
Пример. В магазине продается 14 телевизоров Panasonic и 17 телевизоров Sony. Петя хочет купить один телевизор. Сколько у него вариантов покупки?
Решение. По правилу сложения Петя может выбрать один из 14 + 17 = 31 телевизоров.
Ответ: 31 телевизор.
Особое значение имеет второе правило, которое называют правилом умножения.
Проиллюстрируем это правило.
Решение. Тренер может составить 15•20= 300 разнополых пар из своих воспитанников.
Пример. Пете нужно купить технику для компьютера. В магазине продается 20 различных клавиатур, 25 моделей геймпадов и 30 компьютерных мышей. Купить надо по одному экземпляру каждого из этих устройств. Сколько вариантов покупки есть у него?
Правила сложения и умножения можно комбинировать.
Пример. Сколько слов не более чем из трех букв можно составить, используя алфавит, содержащий ровно 30 букв?
Решение. Очевидно, что слов из одной буквы можно составить ровно 30. Количество двухбуквенных слов равно количеству пар, которые можно составить из этих букв, то есть 30•30 = 900. Трехбуквенных слов можно составить 30•30•30 = 27000. Всего же слов длиною не более 3 букв будет
30 + 900 + 27000 = 27930
Далее мы изучим основные понятия комбинаторики – перестановки, размещения, сочетания.
Перестановки
Рассмотрим простейшую комбинаторную задачу. На полке расставляют по порядку книги. Их ставят вертикально друг за другом. Сколькими способами можно расставить на полке 2 книги? Очевидно, что двумя:
Либо синяя книжка будет первой слева, либо она будет находиться в конце полки, третьего варианта здесь нет. Здесь условно считается, что варианты, когда между книгами есть зазоры, идентичны вариантам без зазоров:
То есть нас интересует исключительно порядок, в котором стоят книги. Каждый из найденных вариантов называется перестановкой книг. Перестановкой называют любое конечное множество, для элементов которого указан порядок элементов.В комбинаторике перестановки являются одними из основных объектов изучения.
Например, если в забеге на 100 метров стартует 8 спортсменов, то они образуют множество участников забега. После финиша становится известно, кто занял 1-ое место, кто оказался вторым или третьим, а кто стал последним. Результат забега будет перестановкой, ведь он представляет собой список спортсменов с указанием их мест, то есть он определяет порядок между ними.
Вернемся к примеру с книгами. Обозначим количество возможных перестановок n элементов как Рn. Две книжки можно расставить двумя разными способами, поэтому Р2 = 2. Обозначим эти перестановки как АБ и БА. Сколько способов расстановки есть в случае трех книжек? Их все можно получить из вариантов с 2 книжками, добавляя между ними книгами ещё один том:
Видно, что между 2 книгами есть три позиции, на которые можно поставить 3-ий том. Общее количество вариантов равно произведению числа этих позиций и количества вариантов для 2 книг, то есть Р3 = 3•Р2 = 3•2 = 6:
Итак, мы имеем 6 перестановок для 3 книг:
А сколько перестановок существует для 4 книг? Снова-таки, между тремя книгами 4-ый том можно поставить четырьмя способами:
То есть из перестановки трех книг АБВ можно получить 4 перестановки:
Всего существует 6 перестановок для 3 книг (Р3 = 6), и для каждой из них можно построить 4 перестановки из 4 книг. Получается, что общее количество перестановок 4 книг равно
Продолжая подобные рассуждения, можно убедиться, что количество перестановок 5 предметов в 5 раз больше, чем перестановок для 4 объектов:
И вообще, если число перестановок n объектов равно Рn, то количество перестановок (n + 1)объекта равно в (n + 1)раз больше:
При этом отметим, что 1 книгу можно расставить на полке только одним способом:
То есть Р1 = 1. Теперь выпишем значения чисел Р при разном количестве переставляемых предметов, используя формулуРn+1 = (n + 1)Рn
Видно, что количество перестановок n объектов равно произведению всех натуральных чисел от 1 до n. В математике есть специальная функция для вычисления значения этого произведения. Она называется факториалом и обозначается восклицательным знаком.
Например, факториал 6 вычисляется так:
Мы убедились на примере с книгами, что количество перестановок из n различных объектов, которое обозначается как Рn, равно n!.
Относительно факториала надо заметить несколько важных моментов. Во-первых, очевидно, что факториал единицы равен 1:
Во-вторых, иногда в комбинаторных задачах приходится вычислять факториал нуля. По ряду соображений эта величина также принимается равной единице
Объяснить это можно так. Факториал числа можно представить как произведение этого числа и факториала предыдущего числа, например:
5! = 1•2•3•4•5 = (1•2•3•4)•5 = 4!•5
7! = 1•2•3•4•5•6•7 = (1•2•3•4•5•6)•7 = 6!•7
В общем случае формула выглядит так:
Из неё несложно получить, что
Подставив в эту формулу единицу, получим
Пример. Сколькими способами тренер может расставить 4 участников эстафеты 4х400 м по этапам эстафеты?
Решение. Количество таких способов равно числу перестановок 4 различных объектов Р4:
Пример. Вася решил изучать сразу 7 иностранных языков, причем на занятия по каждому из них он собирается выделить ровно один день в неделе. Сколько вариантов расписаний занятий может составить себе Вася?
Решение. В данном случае расписание занятий – это порядок, в котором Вася в течение недели будет изучать иностранные языки, например:
Такое расписание можно описать последовательностью символов:
Ф, Ан, И, К, Я, Ар, П
Создавая расписание, Вася переставляет 7 языков, поэтому общее количество расписаний равно 7!:
Пример. Сколько пятизначных цифр можно записать, используя цифры 0, 1, 2, 3, 4, причем каждую не более одного раза?
Решение. Общее количество перестановок 5 цифр составляет Р5. Однако нельзя начинать запись числа с нуля. Так как, перестановка 12340 – это пятизначное число (двенадцать тысяч триста сорок), а перестановка 03241 – не является пятизначным числом.
Расстановок, начинающихся с нуля, ровно Р4, поэтому общее количество допустимых цифр равно Р5 – Р4:
Р5 – Р4 = 5! – 4! = 120 – 24 = 96
Пример. На полке расставляют 7 книг, однако 3 из них образуют трехтомник. Тома трехтомника должны стоять друг за другом и в определенном порядке. Сколько существует способов расстановки книг?
Решение. Будем считать трехтомник одной книгой. Тогда нам надо расставить 5 книг
Пример. Необходимо расставить 7 книг на полке, но три из них принадлежат одному автору. Их надо поставить друг с другом, но они могут стоять в любом порядке. Сколько возможно перестановок книг.
Решение. Снова будем считать три книги как один трехтомник. Получается, что существует 5! = 120 вариантов. Однако каждому из них соответствует 3! = 6 расстановок книг внутри трехтомника, например:
В итоге на каждую из 120 расстановок приходится 6 вариантов расстановки трехтомника, а общее число расстановок равно, согласно правилу умножения, произведению этих чисел:
Перестановки с повторениями
До этого мы рассматривали случаи, когда все переставляемые объекты были различными. Однако порою некоторые из них не отличаются друг от друга. Пусть на полке надо расставить 3 книги, но две из них одинаковые. Сколько тогда существует перестановок? Общее число перестановок 3 книг составляет 3! = 6:
1-ая группа: БАА1А2, БАА2А1, БА1АА2, БА1А2А, БА2АА1, БА2А1А
2-ая группа: АБА1А2, АБА2А1, А1БАА2, А1БА2А, А2БАА1, А2БА1А
3-ая группа: АА1БА2, АА2БА1, А1АБА2, А1А2БА, А2АБА1, А2А1БА
4-ая группа: АА1А2Б, АА2А1Б, А1АА2Б, А1А2АБ, А2АА1Б, А2А1АБ
И снова для подсчета числа оригинальных перестановок надо из общее число расстановок поделить на количество дубликатов в каждой группе:
Для обозначения перестановок с повторениями используется запись
где n – общее количество объектов, а n1, n2, n3,… nk – количество одинаковых элементов. Например, в задаче с 4 книгами мы искали величину Р4(3, 1), потому что всего книг было 4, но они были разбиты на две группы, в одной из которых находилось 3 одинаковых тома (буквы А, А1, А2), а ещё одна книга (Б) составляла вторую группу. Мы заметили, что для вычисления числа перестановок с повторениями надо общее число перестановок делить на количество дублирующих перестановок. Формула в общем случае выглядит так:
Пример. Вася решил, что ему стоит изучать только два иностранных языка. Он решил 4 дня в неделю тратить на английский, а оставшиеся три дня – на испанский. Сколько расписаний занятий он может себе составить.
Решение. Вася должен расставить 3 урока испанского и 4 урока английского, тогда n1 = 3, а n2 = 4. Общее количество уроков равно 3 + 4 = 7. Тогда
Обратите внимание, что для удобства при делении факториалов мы не вычисляли их сразу, а пытались сократить множители. Так как в ответе любой комбинаторной задачи получается целое число, то весь знаменатель дроби обязательно сократится с какими-нибудь множителями в числителе.
Пример. У мамы есть 3 яблока, 2 банана и 1 апельсин. Эти фрукты она распределяет между 6 детьми. Сколькими способами она может это сделать, если каждый должен получить по фрукту?
Решение. Всего есть три группы фруктов. В первой находится 3 яблока, поэтому n1 = 3. Во второй группе 2 банана, поэтому n2 = 2. В третьей группе только 1 апельсин, поэтому nk = 1. Общее число фруктов равно 6. Используем формулу:
В знаменателе формулы для перестановок с повторениями мы записываем число объектов в каждой группе одинаковых предметов. Так, если переставляются 3 яблока, 2 банана и 1 апельсин, то в знаменателе мы пишем 3!•2!•1!. Но что будет, если в каждой группе будет находиться ровно один уникальный объект? Тогда мы запишем в знаменателе произведение единиц:
В итоге мы получили ту же формулу, что и для перестановок без повторов. Другими словами, перестановки без повтора могут рассматриваться просто как частный случай перестановок с повторами.
Размещения
Пусть в футбольном турнире участвуют 6 команд. Нам предлагают угадать те команды, которые займут призовые места (то есть первые три места). Сколько вариантов таких троек существует?
Сначала запишем ту команду, которая выиграет турнир. Здесь есть шесть вариантов, по количеству участвующих команд. Запишем эти варианты:
Далее выберем один из вариантов и для него укажем серебряного призера соревнований. Здесь есть только 5 вариантов, ведь 1 из 6 команд уже записана на 1-ом месте:
В данном случае из некоторого множества команд мы выбрали несколько и расположили их в каком-то порядке. То есть мы выбрали упорядоченное множество. В комбинаторике оно называется размещением.
Если общее число команд обозначить как n (в этом примере n = 6), а количество упорядочиваемых команд равно k, то количество таких размещений в комбинаторике обозначается как
В примере с командами количество размещений равнялось 120:
Для нахождения этого числа мы перемножили k (3)множителей. Первый из них был равен n(6), так как каждая из n команд могла занять первая место. Второй множитель был равен (n– 1), так как после определения чемпиона мы могли поставить на вторую позицию одну из (n– 1) команд. Третий множитель был равен (n– 2). По этой логике каждый следующий множитель будет меньше предыдущего на единицу. Например, чтобы вычислить число размещений из 7 по 4, надо перемножить 4 множителя, первый из которых равен 7, а каждый следующий меньше на 1:
Однако математически удобнее представлять это произведение как отношение двух факториалов. Для этого умножим количество размещений на дробь 3!/3!, равную единице. Естественно, число размещений из-за умножения на единицу не меняется:
Число 3 в данном случае можно получить, если из 7 вычесть 4. В общем случае из числа n надо вычесть число k. Тогда формула для вычисления количества размещений примет вид:
Решение. Для составления расписания нужно выбрать 5 предметов и расставить их по порядку. Поэтому нам необходимо найти размещение из 12 по 5:
Пример. В вагоне 10 свободных мест. В него зашло 6 пассажиров. Сколькими способами они могут расположиться в вагоне?
Решение. Из десяти мест надо выбрать шесть и указать для каждого, какому пассажиру оно соответствует. То есть каждый вариант рассадки пассажиров – это размещение из 10 по 6. Найдем их количество:
Заметим, что перестановка – это частный случай размещения, когда k = n. Действительно, если нам надо указать тройку призеров турнира, в котором участвуют 6 команд, то мы указываем размещение из 6 по 3. Но если мы указываем для каждой из 6 команд, какое место она займет в чемпионате, то это размещение из 6 по 6. С другой стороны, это расстановка одновременно является и перестановкой 6 команд. Убедимся, что в этом частном случае формула для подсчета количества размещений покажет тот же результат, что и формула для перестановок
Для примера с 6 командами это будет выглядеть так:
Здесь мы использовали тот факт, что факториал нуля принимается равным единице. Данное рассуждение можно, наоборот, использовать для того, чтобы доказать, что факториал нуля – это единица.
Сочетания
Однако порою этот порядок не имеет значения. Так, существует известная лотерея, где предлагается угадать 7 чисел из 49, которые выпадут во время розыгрыша из барабана. При этом порядок их выпадения не играет никакой роли. Игрок, выбирая эти 7 чисел, с точки зрения математики формирует сочетание из 49 по 7.
Количество возможных сочетаний из n по k обозначается буквой С:
Для вычисления количеств сочетаний из n по k сначала найдем количество аналогичных размещений. Оно вычисляется по формуле:
Однако ясно, что, как и в случае с перестановками с повторениями, некоторые сочетания мы посчитали несколько раз. Вернемся к примеру с командами. Если мы выбрали команды Л (Локомотив) , З (Зенит) и К (Краснодар), то мы можем составить ровно 3! = 6 размещений из них:
Однако все они соответствуют только одному сочетании – ЛКЗ. Таким образом, считая количество размещений, мы посчитали каждое сочетание не один, а 3! раз. Поэтому для нахождения количества сочетаний в комбинаторике надо поделить число размещений на число перестановок k элементов:
Эта формула связывает важнейшие понятия комбинаторики – перестановки, сочетания и размещения. Подставим в неё формулы для размещений и перестановок и получим:
Пример. Сколько троек призеров турнира можно составить, выбирая три футбольные команды из шести?
Решение. Посчитаем число сочетаний из 6 по 3:
Решение. В каждом из этих случаев игрок выбирает сочетание нескольких чисел. Посчитаем их число:
Ответ: 376992; 8145060; 85900584
Пример. На плоскости отмечены 8 точек, причем никакие три из них не лежат на одной прямой. Сколько различных прямых можно провести через них? Сколько треугольников и четырехугольников можно построить с вершинами в этих точках?
Решение. Для того чтобы провести прямую, достаточно выбрать любые 2 точки из 8. Общее количество прямых будет равно числу сочетаний из 8 по 2:
Заметим принципиальную важность того условия, что никакие три точки не лежат на одной прямой. Оно гарантирует, что при выборе двух различных точек мы будем получать различные прямые. Если бы, например, точки АВС лежали бы на одной прямой, то при выборе сочетаний АВ, ВС и АС мы получали бы одну и ту же прямую:
Это же условие гарантирует, что, выбрав любые 3 и 8 точек, мы сможем построить треугольник с вершинами в этих точках, а выбрав 4 точки, получим четырехугольник. Поэтому для подсчета количества треугольников и четырехугольников следует искать число сочетаний по 3 и 4:
Ответ: 28 прямых, 56 треугольников и 70 четырехугольников.
Пример. В одной урне находится 10 различных шаров с номерами от 0 до 9, а в другой – 8 различных шаров с первыми восемью буквами алфавита. По условиям лотереи ведущий вытаскивает из первой урны два шара с числами, а из второй – три шара с буквами. Для победы в лотерее надо угадать выпавшие шары. Сколько комбинаций шаров может выпасть в игре?
Решение. Посчитаем отдельно, сколькими способами можно выбрать 2 шара с цифрами из 10 и 3 шара с буквами из 8:
По правилу умножения мы должны перемножить эти числа, чтобы найти общее количество возможных вариантов:
Заметим, что выбирая, например, сочетание из 49 по 7, мы одновременно выбираем и сочетание из 49 по 49 – 7 = 42. Действительно, игрок, обводящий в кружок в лотерейном билете свои 7 счастливых чисел, одновременно и определяет остальные 42 числа, какие числа он НЕ считает счастливыми. Для наглядности запишем число сочетаний в обоих случаях:
Получили одну и ту же дробь, в которой отличается лишь последовательность множителей в знаменателе. Можно показать, что и в общем случае число сочетаний из n по k совпадает с количеством сочетаний из n по (n– k):
Читайте также:


