Как сделать кластерный анализ в r

Обновлено: 23.01.2025

Цель работы: научить студентов методам группирования многомерных данных, показать возможности визуализации последовательного формирования кластеров сходных объектов, продемонстрировать вариативность методов кластеризации.

Оглавление

Пакет Statistica 6.0

Иерархическая кластеризация

Пример основан на выборке данных об автомобилях. Открыть файл Cars.sta (через директорию Datasets / Examples), в котором находятся следующие переменные:

• Цена машины (переменная Price);
• Время разгона автомашины (переменная Acceler);
• Время торможения (со скорости 80 миль/час до полной остановки – переменная Braking);
• Коэффициент управляемости (переменная Handling);
• Пробег на галлон топлива (переменная Mileage).

1. Шкала измерений

Все алгоритмы кластеризации вычисляют расстояние между объектами или кластерами, поэтому при использовании переменных, измеренных в различных единицах, необходимо привести данные к такой шкале, посредством которой можно производить действия с переменными. Обычно этой возможности достигают с помощью стандартизации данных (командой Standardize из меню Data), в результате которой каждая переменная имеет нулевое среднее значение и единичную дисперсию. Важно отметить, что значения переменных, которые используются при вычислении расстояний, должны иметь сравнимые величины, так как в противном случае результаты кластерного анализа окажутся смещенными. В файле Cars.sta операция стандартизации уже выполнена.

Файл данных приведен на рис. 1.

Группирование автомобилей по набору переменных.

Рис. 1. Файл данных (стандартизованные величины)

Выбрать модуль Cluster Analysis из меню Statistics - Multivariate Exploratory Techniques для отображения стартовой панели Clustering Method. Далее, выбрать опцию Joining (tree clustering) и нажать ОК. В появившемся окне Cluster Analysis: Joining (Tree Clustering) указать позицию Variables для отображения окна диалога по выбору переменных (select variables), в котором необходимо отметить все переменные, после чего, нажав ОК, возвратиться к окну кластерного анализа (рис. 2).

Вследствие того, что в рассматриваемом примере группируются автомобили (строки исходной матрицы данных), то при положении окна кластерного анализа в опции Advanced в позиции Cluster нужно выбрать Cases (rows). В зависимости от целей исследования могут группироваться и признаки (столбцы матрицы данных); в этом случае в окне Cluster выбирается Variables (columns). Кроме того, в раскрывающемся окне правил объединения (Amalgamation (linkage) rule) указать метод полной связи (Complete Linkage). Окно анализа примет вид, показанный на рис. 3.

Рис. 2. Окно кластерного анализа

Рис. 3. Окно кластерного анализа после выбора переменных

Методы кластеризации успешно работают на основе сходства (различия) между объектами. Естественной оценкой сходства является расстояние, которое рассчитывается в методах кластеризации. В качестве оценок расстояний могут быть выбраны следующие:

Евклидово расстояние: distance (x, y) = i (x_i – y_i) 2 > 1/2 ;

Квадрат евклидова расстояния: distance (x, y) = S_i (x_i – y_i) 2 ;

Манхеттенское расстояние: distance (x, y) = S_i |x_i – y_i|;

Чебышевское расстояние: distance (x, y) = Maximum |x_i – y_i|;

Степенное расстояние: distance (x, y) = (S_i |x_i – y_i| p ) 1/r .

В данном примере выберем в качестве меры расстояния – евклидово и отметим этот выбор в окне расстояний.

Выбор метода объединения определяется значениями коэффициентов в формуле Ланса-Уильямса, используемой в кластерном анализе и зависит от целей анализа. В любом случае полученная группировка объектов должна проверяться различными методами и оцениваться на основании логики и здравого смысла. Здесь вначале выберем правило группирования в виде полных связей (Complete Linkage).

Нажав ОК, приходим к окну результатов кластерного анализа (рис. 4).

Рис. 4. Окно результатов кластерного анализа

В этом окне можно выбрать вид полученной дендрограммы: горизонтальной (Horizontal hierarchical tree) или (Vertical icicle plot), указать тип ветвей этого дерева (прямоугольные или наклонные), получить и проанализировать матрицу расстояний между объектами, построить последовательный график объединения объектов и просмотреть ход группирования. На рис. 5 и 6 показаны, соответственно, в качестве примеров вертикальная дендрограмма и график объединения.

Рис. 5. Дендрограмма объектов

Рис. 6. График объединения

Провести такой анализ для других данных.

Кластеризация методом k-средних

Сущность этого метода заключается в нахождении оптимального деления объектов на k классов. Эта процедура перемещает объекты из кластера в кластер с целью минимизации внутрикластерной дисперсии и максимизации межкластерной дисперсии.

Пример основан на выборке данных об автомобилях. Открыть файл Cars.sta (через директорию Datasets/Examples). Примем, что исходные данные (автомобили) нужно разделить на 3 кластера.

Выбрать модуль Cluster Analysis из меню Statistics - Multivariate Exploratory Techniques для отображения стартовой панели Clustering Method. Далее, выбрать опцию K-means clustering и нажать ОК. В появившемся окне Cluster Analysis: K-means Clustering указать позицию Variables для отображения окна диалога по выбору переменных (select variables), в котором необходимо отметить все переменные, после чего, нажав ОК, возвратиться к окну кластерного анализа. Так как мы хотим получить 3 кластера автомобилей, необходимо ввести это значение в окно Number of clusters, а в окне Cluster указать: Cases (rows) (рис. 7).

Рис. 7. Окно диалога кластерного анализа методом k-средних

Число итераций (Number of iterations). Это окно используется для установления максимального числа итераций, которые должны быть выполнены. Метод k-средних представляет собой итеративную процедуру, и на каждом шаге объекты перемещаются в различные кластеры. Алгоритм, выполняющий этот процесс, в данном модуле достаточно эффективен, поэтому установленное по умолчанию число итераций, равное 10, обычно не требуется увеличивать.

Начальные центры кластеров. При выборе начальных центров кластеров возможны 3 ситуации, описанные ниже. Отметим, что результаты кластеризации методом k-средних зависят от начального выбора центров:

• Выбор наблюдений для максимизации начальных межкластерных расстояний. При выборе этой опции наблюдения или объекты рассматриваются как начальные центры кластеров. Подчеркнем особенности алгоритма в этом случае:

1. Алгоритм будет отбирать первые N строк (число кластеров) как центры кластеров.
2. Последующие строки будут заменять предыдущие центры кластеров, если их наименьшее расстояние до любого центра кластеров оказывается больше, чем наименьшее расстояние между кластерами.
3. В противном случае последующие строки будут заменять начальные центры кластеров, если их наименьшее расстояние от центра кластера больше, чем расстояние от этого центра кластера до любого другого кластерного центра.

Эффект такой процедуры отбора заключается в максимизации начальных расстояний между кластерами.

• Упорядочение расстояний и отбор наблюдений при постоянных интервалах. При выборе этой опции расстояния между всеми объектами вначале будут упорядочены, а затем объекты при постоянных интервалах будут выбраны как центры кластеров.
• Выбор первыхNнаблюдений (числа кластеров).При выборе этой опции первые N наблюдений рассматриваются как начальные центры кластеров. Таким образом, эта опция обеспечивает полный контроль над выбором начальной конфигурации.

В данном примере остановимся на второй опции: Упорядочение расстояний и отбор наблюдений при постоянных интервалах.

При завершении анализа на экране монитора появится окно результатов анализа (K - Means Clustering Results), в котором выделим опцию Advanced (Расширенная) для подробного рассмотрения итогов (рис. 8).

Рис. 8. Окно результатов анализа

Идентификация кластеров

Для рассмотрения состава каждого кластера необходимо нажать клавишу Members of each cluster & distances (Состав каждого кластера и расстояния), после чего появятся 3 таблицы, в которых указаны объекты, попавшие в определенный кластер (рис. 9).

Как видно из приведенных таблиц, каждый кластер содержит различное число объектов: в первом кластере находятся 13 автомобилей, во втором – 7, в третьем – 2.

Рис. 9. Состав кластеров

Описательные статистики для каждого кластера

Другой способ идентификации заключается в рассмотрении средних значений для каждого кластера. Этого можно достичь различными путями, например: отобразить статистики отдельно для каждого кластера (нажать клавишу Descriptive statistics for each cluster), вывести средние для всех кластеров и расстояния между ними в отдельную таблицу (нажать клавишу Summary: Cluster means & Euclidean distances) или построить графики этих средних (нажать клавишу Graph of means). Обычно графики дают наиболее наглядную информацию. В качестве примера на рис.10 приведены графики средних значений.

Рис. 10. Графики средних значений

Пакет Statgraphics. 5.1

Пример основан на выборке данных об автомобилях. Открыть файл Cardata.sf.

Из строки Menu последовательно выбрать SPECIAL … MULTIVARIATE METHODS … CLUSTER ANALYSIS для отображения окна кластерного анализа, показанного на рис. 11.

Рис. 11. Окно кластерного анализа

Двойным щелчком мыши выберем количественные переменные, которые автоматически появятся в поле данных этого окна. Для наглядности итоговых результатов в поле Select укажем первые 20 строк исходной матрицы данных, набрав first (20). Щелкнув ОК, переходим к анализу результатов.

Наиболее часто используемыми процедурами при кластерном анализе являются иерархические и не иерархические способы. В первом случае образуются древоподобные структуры (дендрограммы), независимо от того, применяются ли агломеративные или дивизимные методы. При иерархических агломеративных процедурах каждое наблюдение вначале рассматривается как отдельный кластер, и последующие шаги формируют из этих одноместных объектов новые агрегированные кластеры, уменьшающие их число на каждом шаге. В противном случае кластерные процедуры определяют дивизимные методы (вначале все объекты рассматриваются как один кластер) или метод k -средних.

В данном пакете реализованы алгоритмы расчета 6 методов кластеризации, различающиеся способом объединения объектов. Кратко опишем каждый их них.

Ближний сосед. В этом методе определяются 2 объекта, находящиеся на наименьшем расстоянии, и помещаются в один кластер. Затем определяется следующее минимальное расстояние и к уже сформированному кластеру присоединяется третий объект или образуется новый кластер из двух объектов. Процедура продолжается до тех пор, пока все объекты не сформируют один кластер. Этот метод также носит название одиночной связи.

Дальний сосед. Здесь используется максимальное расстояние между двумя объектами. Все объекты в кластере соединяются один с другим при некотором максимальном расстоянии (минимальном сходстве). Этот метод известен под названием полной связи.

Центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Каждый раз при группировке объектов образуются новые центроиды. Кластерные центроиды перемещаются при добавлении нового объекта (или группы объектов) к существующему кластеру.

Медианный метод. Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т. е. числами объектов в них).

Метод группового среднего. В этом методе расстояние между кластерами вычисляется как среднее расстояние между всеми объектами в одном кластере и средним расстоянием между всеми объектами в другом кластере.

Метод Уорда (Ward). Метод минимизирует сумму квадратов для любых двух кластеров, которые могут быть сформированы на каждом шаге. Этот метод формирует кластеры, которые имеют малое число объектов, и стремится создать кластеры, содержащие примерно одинаковое число объектов.

Нажав на правую кнопку мыши, получим окно диалога для выбора параметров анализа (рис. 12).

Рис. 12. Окно диалога для выбора параметров анализа

В рассматриваемом случае при 20 объектах рекомендуется выбрать метод Уорда, для чего в поле методов раскрывшегося окна укажем этот метод. Кроме того, установим число кластеров, равное 3, на которое желательно разбить исследуемую совокупность. Для этого необходимо ввести это число в поле в нижнем левом углу окна диалога. Нажав ОК, приходим к итоговым результатам.

Среди табличных опций, окно которых открывается второй кнопкой слева в строке меню, выделим следующие три позиции (см. рис. 13):

Рис. 13. Окно табличных опций

Эти таблицы показывают, соответственно, итоговый анализ, состав кластеров и расписание (последовательность) объединения.

Среди графических опций (третья кнопка слева) выделим такие позиции (см. рис. 14):

Рис. 14. Окно графических опций

Выделенные опции показывают дендрограмму анализа и график объединения. Наиболее интересной оказывается дендрограмма, приведенная на рис. 15.

Будучи новичком в R, я не очень уверен, как выбрать лучшее количество кластеров для анализа k-средних. После построения подмножества данных ниже, сколько кластеров будет уместным? Как я могу выполнить кластерный анализ дендро?

Если ваш вопрос how can I determine how many clusters are appropriate for a kmeans analysis of my data? , то вот несколько вариантов. Википедия статья об определении числа кластеров имеет хороший обзор некоторых из этих методов.

Во-первых, некоторые воспроизводимые данные (данные в Q . для меня неясны):

Мы могли бы заключить, что 4 кластера будут обозначены этим методом:

Два . Вы можете выполнить разбиение вокруг медоидов, чтобы оценить количество кластеров, используя pamk функцию в пакете fpc.

Три . Критерий Калинского: еще один подход к диагностике того, сколько кластеров соответствует данным. В этом случае мы пробуем от 1 до 10 групп.

Четыре . Определить оптимальную модель и количество кластеров согласно байесовскому информационному критерию для максимизации ожидания, инициализированному иерархической кластеризацией для параметризованных моделей гауссовой смеси

Шесть . Статистика разрыва для оценки количества кластеров. Смотрите также некоторый код для хорошего графического вывода . Попытка 2-10 кластеров здесь:

Вот результат реализации статистики разрыва Эдвином Ченом:

Восемь . Пакет NbClust предоставляет 30 индексов для определения количества кластеров в наборе данных.

Вот несколько примеров:

Также для данных большого размера есть pvclust библиотека, которая вычисляет p-значения для иерархической кластеризации с помощью мультимасштабной начальной загрузки. Вот пример из документации (не будет работать с такими низкоразмерными данными, как в моем примере):

Помогает ли что-нибудь из этого?

Для последней дендограммы (кластерная дендограмма с AU / BP) иногда удобно рисовать прямоугольники вокруг групп с относительно высокими значениями p: pvrect (fit, alpha = 0,95)

Это именно то, что я искал. Я новичок в R, и мне потребовалось бы очень много времени, чтобы найти это. Спасибо @Ben за ответ в таких деталях. Не могли бы вы подсказать мне, где я могу найти логику каждого из этих методов, например, какой показатель или критерий они используют для определения оптимального числа кластеров, или как каждый из них отличается друг от друга. Мой начальник хочет, чтобы я сказал это, чтобы мы могли решить, какой из методов использовать. Заранее спасибо.

@AndreySapegin: Могу, но: 1) честно говоря, я не считаю это элегантным решением (ИМХО, в большинстве случаев визуальные методы должны оставаться визуальными, а аналитические - аналитическими); 2) Я нашел аналитическое решение для этого, используя один или несколько R пакетов (он находится на моем GitHub - вы можете посмотреть); 3) мое решение, кажется, работает достаточно хорошо, к тому же прошло много времени, и я уже завершил подготовку своего диссертационного программного обеспечения, отчета по диссертации (тезис) и в настоящее время я готовлюсь к защите :-). Несмотря на это, я очень ценю ваш комментарий и ссылки. Всего наилучшего!

2,2 миллиона строк в моем текущем наборе данных кластеризации. Я предполагаю, что ни один из этих пакетов R не работает на нем. Они просто выскакивают из моего компьютера, а потом это падает из моего опыта. Тем не менее, похоже, что автор знает свое дело для небольших данных и для общего случая, независимо от емкости программного обеспечения. Баллы не вычитаются из-за очевидной хорошей работы автора. Вы, пожалуйста, просто знайте, что старый добрый R ужасен на 2,2 миллиона строк - попробуйте сами, если не доверяете мне. H2O помогает, но ограничен небольшим огороженным садом счастья.

Трудно добавить что-то слишком сложный ответ. Хотя я чувствую, что мы должны упомянуть identify здесь, особенно потому, что @Ben показывает много примеров дендрограмм.

identify позволяет вам интерактивно выбирать кластеры из дендрограммы и сохраняет ваши выборы в списке. Нажмите Esc, чтобы выйти из интерактивного режима и вернуться в консоль R. Обратите внимание, что список содержит индексы, а не имена строк (в отличие от cutree ).

Для определения оптимального k-кластера в методах кластеризации. Я обычно использую Elbow метод, сопровождаемый параллельной обработкой, чтобы избежать затрат времени. Этот код может привести пример:

Метод локтя

Бег Локоть параллельно

Это работает хорошо.

Великолепный ответ от Бена. Однако я удивлен, что метод Affinity Propagation (AP) был предложен здесь только для того, чтобы найти номер кластера для метода k-средних, где в общем случае AP лучше выполняет кластеризацию данных. Пожалуйста, смотрите научную статью, поддерживающую этот метод в науке здесь:

Поэтому, если вы не склонны к k-средствам, я предлагаю использовать AP напрямую, что позволит кластеризовать данные без необходимости знать количество кластеров:

Если отрицательные евклидовы расстояния не подходят, то вы можете использовать другие меры подобия, представленные в том же пакете. Например, для сходств, основанных на корреляциях Спирмена, это то, что вам нужно:

Обратите внимание, что эти функции для сходства в пакете AP просто предоставлены для простоты. Фактически, функция apcluster () в R будет принимать любую матрицу корреляций. То же самое ранее с помощью corSimMat () можно сделать с помощью этого:

в зависимости от того, что вы хотите кластеризовать на вашей матрице (строки или столбцы).

Основная идея кластерного анализа (clustering, cluster analysis) заключается в том, чтобы разбить объекты на группы или кластеры таким образом, чтобы внутри группы эти наблюдения были более похожи друг на друга, чем на объекты другого кластера.

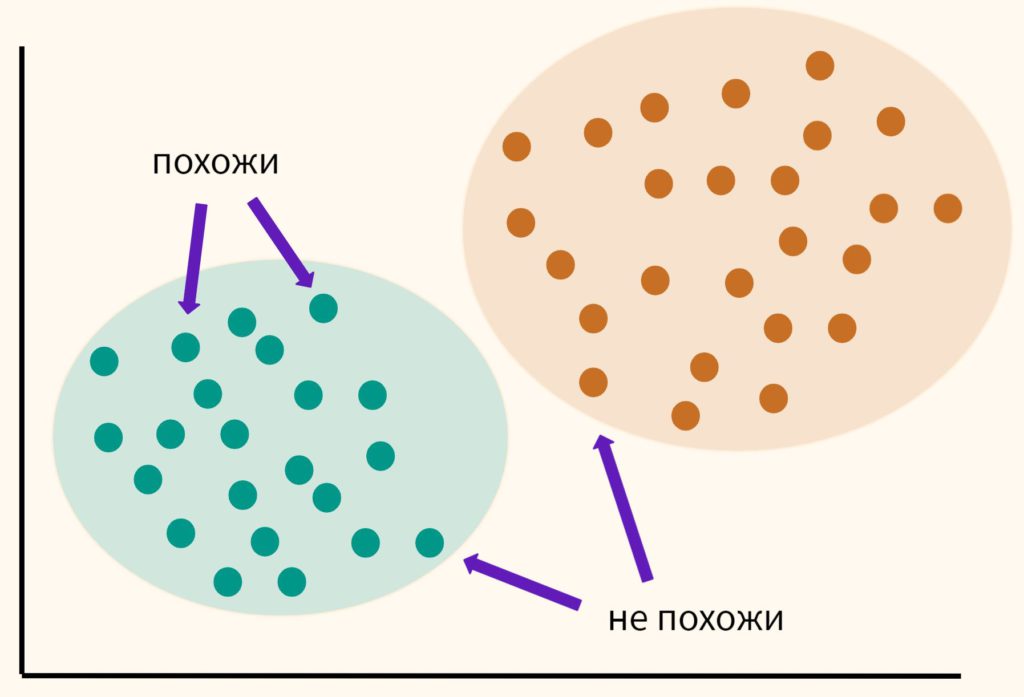
При этом мы заранее не знаем на какие кластеры необходимо разбить наши данные. Это связано с тем, что мы обучаем модель на неразмеченных данных (unlabeled data), то есть без целевой переменной, компонента y. Именно поэтому в данном случае говорят по машинное обучение без учителя (Unsupervised Learning).

Кластерный анализ может применяться для сегментации потребителей, обнаружения аномальных наблюдений (например, при выявлении мошенничества) и в целом для структурирования данных, о содержании которых мало что известно заранее.

Как же разбить данные на кластеры?

Изучая векторы и матрицы, мы узнали, что векторы данных можно сравнивать между собой (оценивать их схожесть), измеряя расстояние между ними. Кластерный анализ использует именно этот подход. Мы измеряем расстояние между точками и на основе этого измерения принимаем решение к какому кластеру отнести то или иное наблюдение.

В рамках этого занятия мы поговорим про алгоритм, который называется методом k-средних (k-means clustering method).

Метод k-средних

Давайте пошагово разберемся в том, как работает этот алгоритм.

Шаг 1. Вначале возьмем данные и самостоятельно выберем желаемое количество кластеров и обозначим их буквой k (отсюда название метода). Пусть в данном случае их будет три.

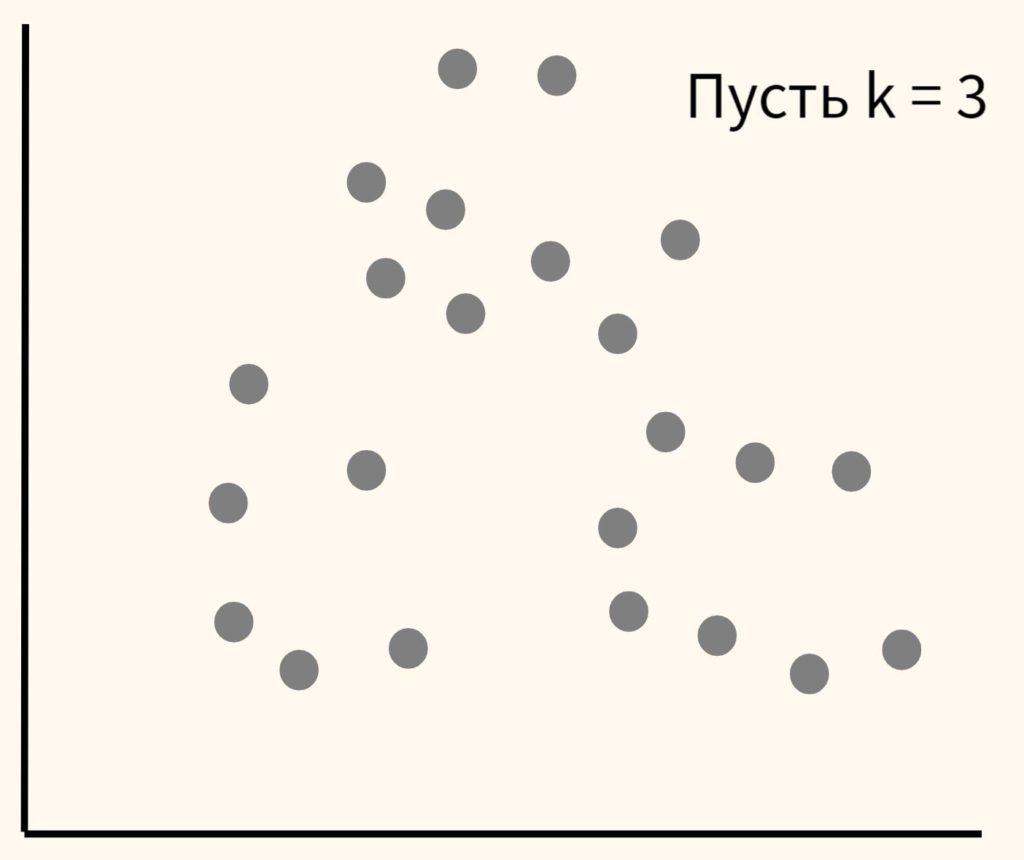
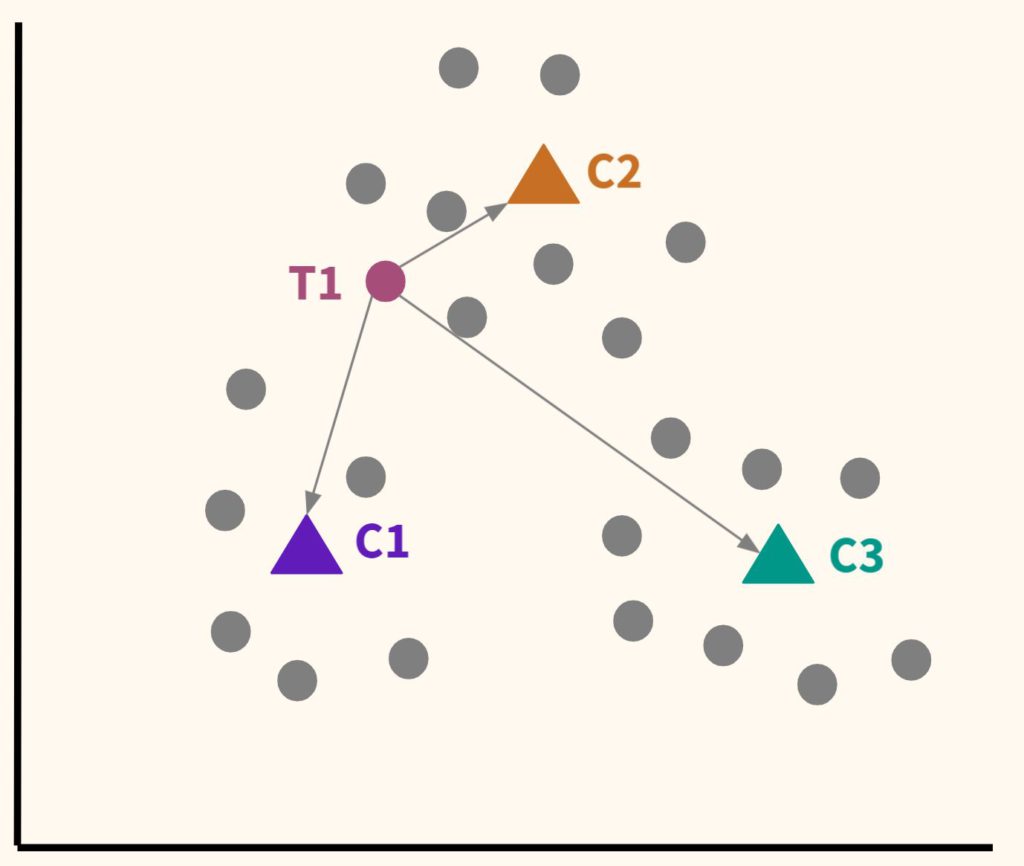
Шаг 2. Расположим несколько точек. Их количество будет равно количеству кластеров. Эти точки называются центроидами. Посчитаем расстояние от наших данных до каждого из центроидов. Логично отнести наблюдение к тому центроиду, который находится ближе.

В частности, T1 будет отнесена к C2.

Шаг 3. Таким образом, каждая точка будет отнесена к определенному центроиду (кластеру).

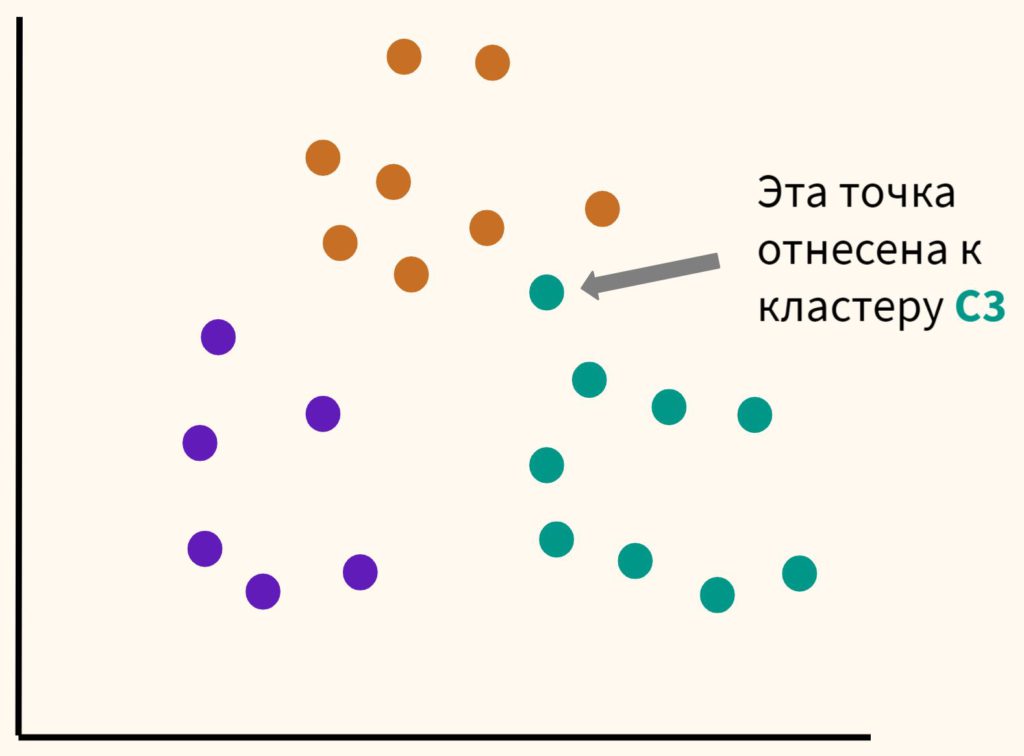
Шаг 4. Сместим наши центроиды в центр получившихся кластеров.

Мы будем повторять шаги 4 и 5 до тех пор, пока алгоритм не стабилизируется, то есть до тех пор, пока наблюдения не перестанут переходить от одного центроида (кластера) к другому.

Говоря более формально, цель алгоритма — минимизировать сумму квадратов внутрикластерных расстояний до центра кластера (within-cluster sum of squares, WCSS, наша функция потерь):

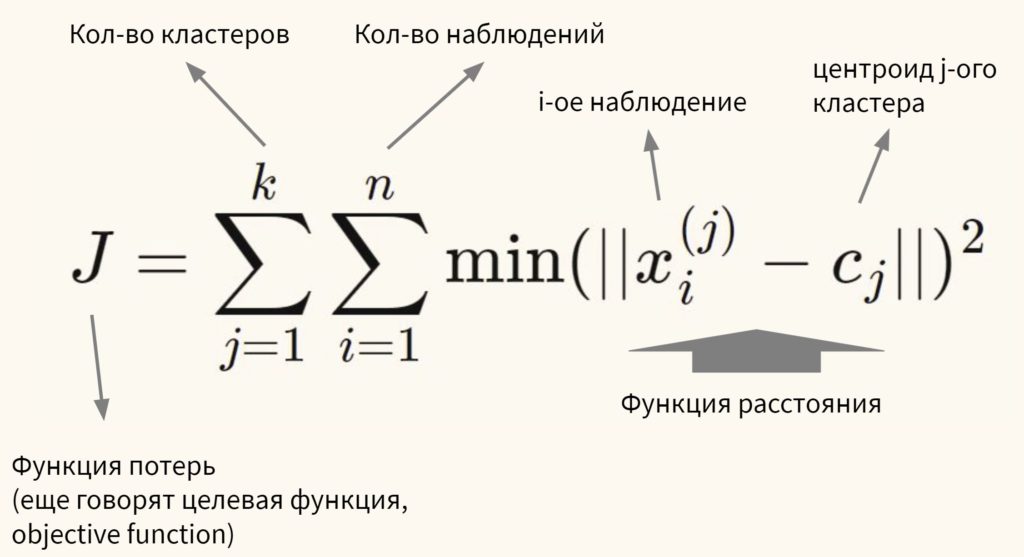
Остается нерешенным важный вопрос.

Сколько кластеров выбрать?

Есть два способа выбора количества кластеров:

1. Экспертный метод. Выбор количества кластеров будет зависеть от знания о предметной области (domain knowledge)
2. Метод локтя (elbow method). Мы также можем (1) обучить модель используя несколько вариантов количества кластеров, (2) измерить сумму квадратов внутрикластерных расстояний и (3) выбрать тот вариант, при котором данное расстояние перестанет существенно уменьшаться.

На графике метод локтя выглядит следующим образом.

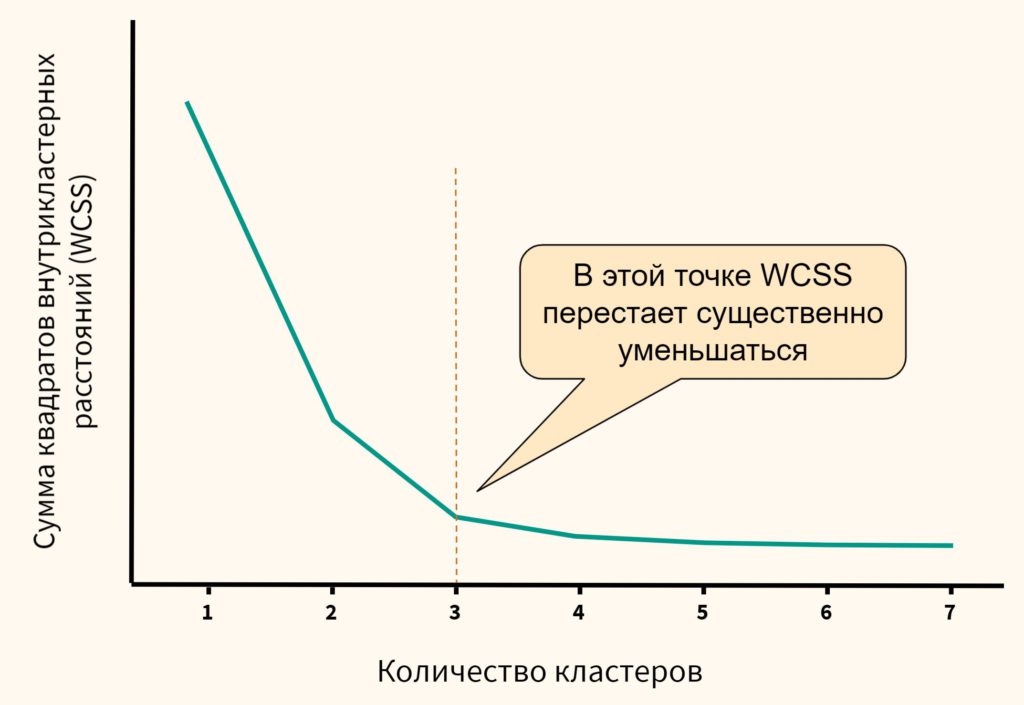
Как мы видим, после того как количество кластеров достигает трех, сумма квадратов внутрикластерных расстояний перестает существенно уменьшаться. Значит в данном случае три кластера и будет оптимальным значением.

О важности нормализации данных

Алгоритм очень чувствителен к масштабу признаков. В связи с этим нормализация данных (feature scaling) приобретает особое значение. Так как при формировании кластеров мы измеряем расстояние (в частности, Евклидово расстояние), то признаки с большим масштабом будут иметь больший вес. Приведу пример.

Предположим у вас есть данные о возрасте и ежемесячных тратах людей по кредитным картам.

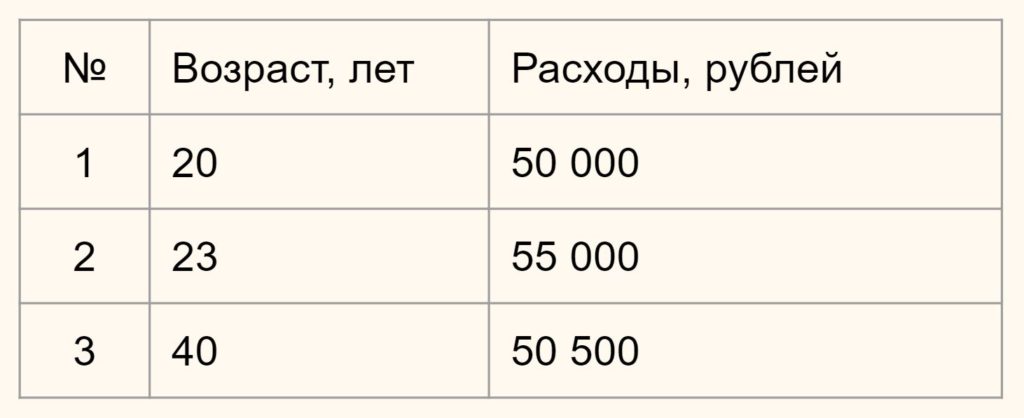
Нам нужно определить насколько человек 1 отличается (насколько велико расстояние) от человека 2 и 3. В зависимости от этого мы будем формировать наши кластеры.

Вначале давайте обратимся к здравому смыслу. Мы видим, что респонденты 1 и 2 схожи, потому что им обоим около 20-ти и расходы у них примерно одинаковы. Респондент 3, имея схожие расходы, сильно отличается из-за своего возраста. Он в два раза старше. Это особенно легко увидеть на графике ниже:

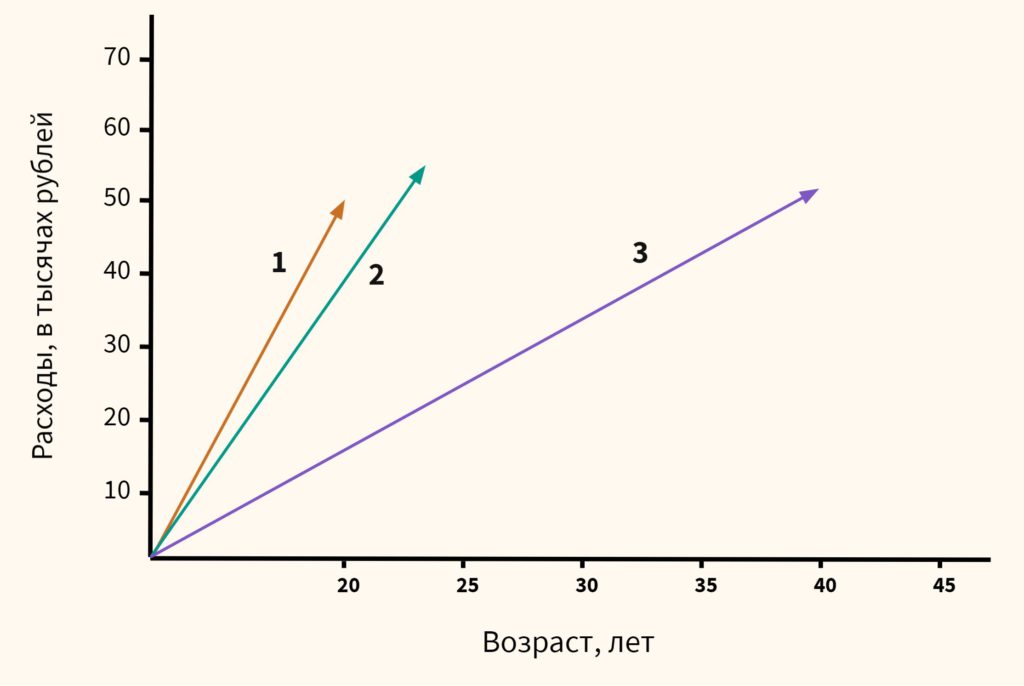
Теперь посмотрим, что скажет математика, если мы оставим масштаб признаков без изменений.

Напомню формулу Евклидова расстояния.

В данном случае x₁ и x₂ — это возраст двух сравниваемых нами людей, а y₁ и y₂ — их расходы. Подставим значения в формулу.

$$ D_1 = \sqrt <\left( <23-20 >\right)^2 + \left( \right)^2 > \approx 5000 $$

Как мы видим, расстояние от человека 1 до человека 2 целых 5000 единиц (лет и рублей), в то время как до человека 3 только 500. Результат обратный тому, на который мы рассчитывали исходя из здравого смысла.

Это связано с тем, что масштаб второго признака (расходов) намного больше масштаба первого (возраст). И даже небольшое изменение в расходах вызывает существенное изменение расстояния, в то время как значительное изменение возраста не оказывает на него практически никакого влияния.

Практический пример — цветы ириса

Для иллюстрации работы алгоритма кластеризации мы возьмем еще один классический датасет из библиотеки sklearn, а именно данные о цветах ириса.

Этап 1. Загрузка данных

Давайте сразу загрузим данные и преобразуем их в формат датафрейма из библиотеки Pandas.

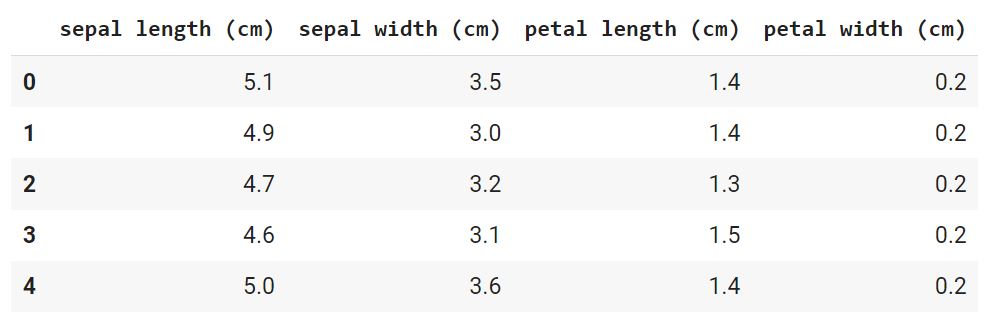
В данном случае речь идет о наборе данных, который состоит из 150 образцов цветов ириса, разделенных на три вида (Iris setosa, Iris virginica и Iris versicolor) по 50 растений в каждом. Каждый образец описан четырьмя атрибутами (длиной и шириной чашелистика и длиной и шириной лепестка).

Обратите внимание, мы сознательно не стали использовать целевую переменную, потому что решаем задачу кластеризации и предполагается, что мы не знаем заранее на какие группы или кластеры удастся разбить наши данные.

С другой стороны, тот факт, что нам заранее известно, что видов здесь три, поможет нам оценить качество кластерного анализа (об этом ниже).

Этап 2. Предварительная обработка данных

Для начала посмотрим, присутствуют ли пропущенные значения.

Мы видим, что пропущенных значений нет. Датасет был предварительно обработан.

Категорийных переменных у нас также нет. Это становится понятно из результата функции head().

Остается разобраться с масштабом признаков. Как уже было сказано, для метода k-средних нормализация данных имеет особое значение. Даже небольшое различие в масштабе признаков может повлиять на конечный результат.

Этап 3 и 4. EDA и отбор признаков

Для целей кластерного анализа мы возьмем все имеющиеся у нас данные.

Этап 5.1. Обучение модели

Самый главный вопрос, который нам предстоит решить на этапе обучения модели заключается в выборе количества кластеров.

Количество кластеров в методе k-средних являтся так называемым гиперпараметром, то есть параметром, который нужно задать до обучения модели.

Мы усложним решаемую нами задачу и сделаем вид, что не обладаем экспертными знаниями о количестве видов ириса (на самом деле напомню, мы знаем, что их три). Значит нужно использовать метод локтя.

kmeans = KMeans ( n_clusters = i , init = 'k-means++' , max_iter = 300 , n_init = 10 , random_state = 42 )

Как видно на графике, когда мы перешли от трех до четырех кластеров, ошибка перестала существенно уменьшаться (это согласуется с тем, что видом действительно три).

Давайте создадим объект класса нашей модели, используя три кластера в качестве гипепараметра модели.

kmeans = KMeans ( n_clusters = 3 , init = 'k-means++' , max_iter = 300 , n_init = 10 , random_state = 42 )

Подробнее рассмотрим параметры модели:

• n_clusters: это количество кластеров, на которые мы хотим разбить наши наблюдения
• init: определяет, как мы выберем первоначальное расположение (инициализацию) центроидов; есть два варианта, (1) выбрать центроиды случайно init = 'random' или (2) выбрать их так, чтобы центроиды с самого начала располагались максимально далеко друг от друга init = 'k-means++' ; второй вариант оптимальнее
• n_init: сколько раз алгоритм будет инициализирован, т.е. сколько раз будут выбраны центроиды до начала оптимизации; на выходе будет выбран тот вариант, где ошибка была минимальна
• max_iter: максимальное количество итераций алгоритма после первоначального выбора центроидов
• random_state: воспроизводимость результата, с этим мы уже знакомы

Обучим модель и сделаем прогноз:

Этап 5.2. Оценка качества модели

Остается проверить качество модели и здесь возникает сложность. Ведь если при обучении с учителем у нас был критерий (целевая переменная), то здесь такого критерия нет.

Впрочем, так как у нас учебный датасет, и мы заранее знаем, к какому виду относится каждый цветок, то можем сравнить результат нашей модели с целевой переменной.

На настоящих данных такое конечно невозможно.

Вначале преобразуем нашу целелевую переменную (iris.target) и наш прогноз (y_pred) в датафрейм (предварительно слегка их изменив, подробности в ноутбуке⧉).

С помощью функции where() создадим массив Numpy, в котором сравним каждую строчку датафрейма, и если целевая переменная и прогноз совпадают, зададим значение True, в противном случае — False.

Добавим этот массив в качестве столбца в датафрейм.

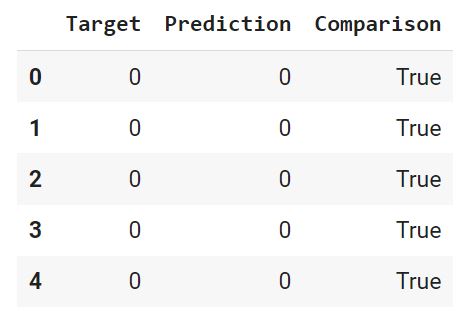
Выведем долю совпавших (True) и не совпавших (False) значений. Для этого используем функцию value_counts(), которая подсчитает, сколько раз встречается каждое значение. Параметр normalize = True вернет относительное значение или процент. Ровно это нам и нужно.

Как мы видим, модель была права в 83% случаев. Теперь давайте визуально оценим результат.

В исходном датафрейме четыре признака, а значит четыре измерения, столько мы представить графически не можем. Давайте возьмем первый (sepal length) и второй (sepal width) столбец исходного датафрейма.

Вначале построим точечную диаграмму целевой переменной.

Теперь посмотим на результат алгоритма кластеризации.

plt . scatter ( kmeans . cluster_centers_ [ : , 0 ] , kmeans . cluster_centers_ [ : , 1 ] , s = 150 , c = 'red' , marker = '^' , label = 'Centroids' )

Выводы. Как мы видим, алгоритм идеально справился с кластером 0 (светлоголубой), однако допустил ошибки при разделение кластеров 1 и 2 (желтый и коричневый цвета). Почему?

Иллюстрация ниже примерно показывает, что сделал алгоритм с нашими исходными видами и почему он ошибочно группировал некоторые точки.

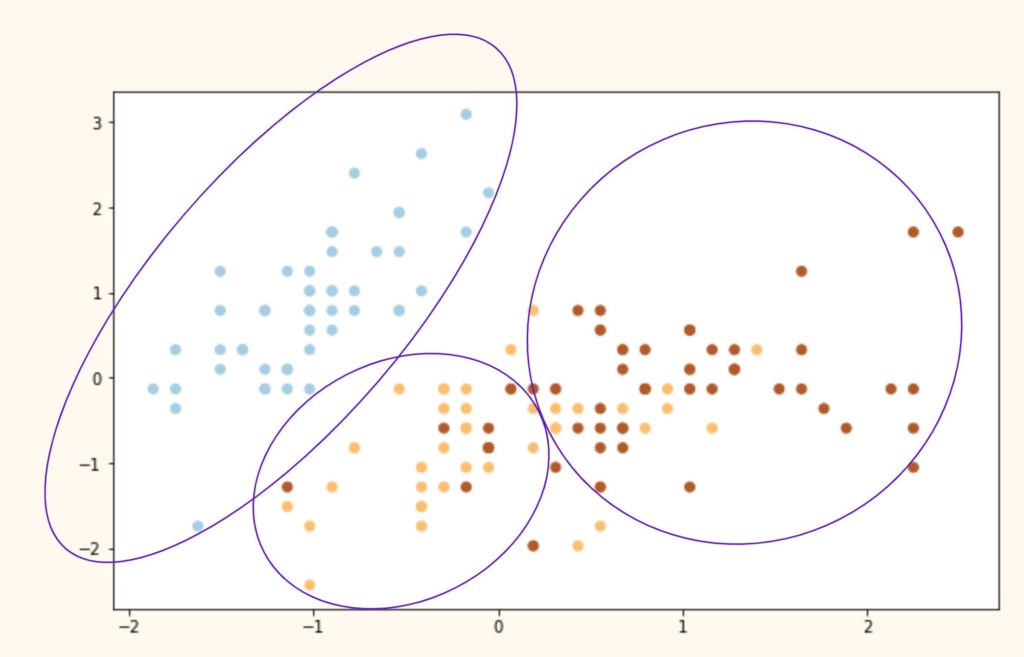
Подведем итог

При решении задач кластеризации мы берем данные, обязательно их масштабируем и выбираем количество кластеров (с помощью экспертной оценки или метода локтя) . К сожалению, дать точную оценку качества кластеризации бывает очень сложно из-за отсутствия разметки.

Вопросы для закрепления

Почему кластеризация называется машинным обучением без учителя?

Посмотреть правильный ответ

Ответ: в таких задачах отсутствует целевая переменная, разметка. Алгоритм пытается структурировать данные, о которых мало что известно заранее.

Как выбирается гиперпараметр модели (количество кластеров)?

Посмотреть правильный ответ

Ответ: существует два способа: (1) экспертное мнение и (2) метод локтя

В чем заключаются основные ограничения модели k-средних?

Посмотреть правильный ответ

Ответ: модель (1) очень чувствительна к масштабу признаков, и кроме того алгоритм предполагает (2) выпуклость и (3) разделенность данных

Дополнительные упражнения⧉ вы найдете в конце ноутбука.

Мы закончили третий раздел классических алгоритмов машинного обучения. Пора переходить к более продвинутым задачам. Начнем с рекомендательных систем.

Здравствуйте! Скажите, а чем init = ‘k-means++’ лучше, чем init = ‘random’? Можете чуть подробнее объяснить. Спасибо!

Максим, спасибо за вопрос. Давайте разбираться. В первую очередь, посмотрим на случайную инициализацию центроидов (). Как следует из самой формулировки, мы случайным образом выбираем центры кластеров, и затем алгоритм, как описано в лекции, старается минимизировать функцию потерь (WCSS в данном случае).

Как мы видим, алгоритм действительно минимизировал WCSS, однако лишь в пределах того, что ему позволил изначальный выбор положения центроидов. Это так называемый локальный минимум функции потерь. Глобальный же найден не был. Схематически глобальный минимум мог бы выглядеться как на графике ниже.

В данном случае глобальный оптимум был бы достигнут за счет максимизации изначального расстояния между центроидами. На этом и основан метод k-means++ ().

Курс посвящен статистическому сравнению характеристик групп и категорий. В первой части курса мы рассказываем о параметрических и непараметрических тестах сравнения средних и распределений, какие возможности и ограничения связаны с разными методами сравнения групп, говорим о сравнении связанных и несвязанных выборок. Различаются ли регионы (или аудитории) по доходу или возрасту? Как отличается пользовательская активность в разные времена года? Случайны различия между группами или закономерны? Курс научит искать ответы на такие вопросы. Вторая половина курсов посвящена выделению групп на основе эмпирических данных. Есть ли структура в данных? Можно ли говорить о том, что люди, компании или университеты группируются в отличительные, узнаваемые классы? Как найти и охарактеризовать такие группы? Мы покажем основные алгоритмы кластеризации, которые позволяют решать такие задачи. В практических видео курса мы покажем реализацию основных инструментов сравнения и выделения групп, а также предложим практические задачи и задания для отработки полученных навыков.

Рецензии

Итерационные методы кластерного анализа

В заключительном модуле курса мы разберемся с еще одним классом методов кластеризации - с итерационными методами: увидим, как работают алгоритмы, каковы возможности и ограничения разных алгоритмов, научимся строить классификации, оценивать их качество, характеризовать и анализировать полученные группы, а также разберем некоторые инструменты визуализации результатов классификации. В заключении, как всегда, практика на реальных данных.

Преподаватели

Olga Echevskaya

доцент, кандидат социологических наук

Виктор Дёмин

Специалист по анализу данных, кандидат технических наук

Наталья Галанова

Специалист по анализу данных

Текст видео

[МУЗЫКА] [МУЗЫКА] [МУЗЫКА] Сегодня мы рассмотрим с вами как построить как построит кластерный анализ с помощью метода k-средних в R. Для начала давайте прочитаем данные. Они у нас лежат в файле dataClust. [БЕЗ СЛОВ] [БЕЗ СЛОВ] Как вы помните, мы кластеризуем с вами университеты по трем показателям. Это средняя зарплата выпускников в Москве, средний балл ЕГЭ при поступлении и процент остающихся в городе обучения. Для того чтобы воспользоваться методом k-средних, нам необходимо выполнить команду kmeans. Как вы помните, в методе k-средних нам необходимо явно задать количество кластеров, которое мы хотим получить, и на основании проведенного уже иерархического анализа, мы с вами выяснили, что оптимальным количеством кластеров для этих данных у нас является 5. Соответственно, в centers мы как раз пишем 5, чтобы он выделил нам 5 кластеров. Также мы говорили с вами, что очень важно для метода k-средних выбор начального приближения, и что наилучшим способом является генерация случайных точек и повторение метода несколько раз из разных начальных приближений. nstart говорит нам о том, сколько делать запусков. В данном случае делаем до 20 запусков. Давайте посмотрим, что же у нас получилось. Здесь мы видим центр кластеров, которые у нас получились по всем трем переменным. Также мы видим результирующий вектор, который показывает нам, к какому кластеру было отнесено то или иное наблюдение. Также здесь внутри мы видим кластерную дисперсию. Давайте нарисуем полученные нами кластеры. [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] Здесь мы видим полученные нами кластеры во всех трех разрезах. Давайте попробуем построить данные в каком-нибудь одном разрезе и также нарисовать центры кластеров, которые мы получили. [БЕЗ СЛОВ] [БЕЗ СЛОВ] Здесь у нас данные по разрезу: зарплата и средний балл ЕГЭ. Сейчас давайте добавим сюда же центры наших кластеров. [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] Соответственно, выглядит это следующим образом. Аналогичные графики можно построить в любом из разрезов. Теперь давайте посмотрим, какая еще информация у нас возвращается в результате кластирезации методом k-средних. Для начала мы можем посмотреть, за какое количество итераций у нас сошелся метод. Здесь мы видим, что он сошелся за 4 итерации. Также мы можем посмотреть, какого размера получились кластеры. Кластеры получились следующего вида. По размеру можно посмотреть на сбалансированность тех или иных кластеров. Например, у нас могут быть кластеры выброса, состоящие из 1–2 наблюдений. Также можем посмотреть на общую дисперсию в данных. Также мы можем посмотреть на внутрикластерную дисперсию. Здесь у нас показана внутрикластерная дисперсия в отдельности по каждому кластеру. Также мы можем посмотреть общую, то есть суммарную внутрикластерную дисперсию. Как вы помните, мы с вами говорили о том, что в качестве меры качества наших кластеров мы можем рассматривать скорректированный R-квадрат. Давайте посчитаем его для наших кластеров. [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] [БЕЗ СЛОВ] Как вы помните, скорректированный R-квадрат показывает нам долю объясненной дисперсии, то есть долю общей дисперсии в данных, которые объясняются нашим разбиением на группы, на кластеры. Соответственно, чем эта доля больше, тем лучше у нас получился кластерный анализ. Как мы видим, у нас значение получилось 0,78, что достаточно неплохо. Таким образом, мы рассмотрели с вами, как построить кластерный анализ с помощью метода k-средних в R. Посмотрели, как получить результаты, как их визуализировать, как посмотреть какую-то дополнительную информацию, например, о том, за какое количество итераций сошелся метод, какой у нас получился объем кластеров. И также

Пример решения задачи на базе аналитической low-code платформы Loginom:

Кластеризация — объединение объектов или наблюдений в непересекающиеся группы, называемые кластерами.

Ирисы Фишера — это набор данных для задачи классификации, на примере которого Р. Фишер (1936 г.) продемонстрировал работу разработанного им метода дискриминантного анализа. Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров из трёх видов — Ирис щетинистый (Iris setosa), Ирис виргинский (Iris virginica) и Ирис разноцветный (Iris versicolor). Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):

• Длина чашелистика (SepalLength);
• Ширина чашелистика (SepalWidth);
• Длина лепестка (PetalLength);
• Ширина лепестка (PetalWidth).

Ирисы Фишера хорошо поддаются кластеризации метрическими алгоритмами.

Исходные данные

Имя поля	Метка поля
SepalLength	Длина чашелистика
SepalWidth	Ширина чашелистика
PetalLength	Длина лепестка
PetalWidth	Ширина лепестка
Class	Класс

Алгоритм

1. Импорт исходных данных;
2. Кластеризация:
   ;
   • Кластеризация k-means;
   • Кластеризация g-means.

Сценарий

EM Кластеризация

Рассмотрим настройки обработчика EM кластеризация:

Результаты EM кластеризации представлены в разделе Интерпретация.

Кластеризация (k-means)

Примечание: отличие Кластеризации k-means от g-means в том, что если количество кластеров известно, то применяется алгоритм k-means, в противном случае g-means, который определит это количество автоматически в рамках заданного интервала. В Loginom для этого используется один и тот же обработчик Кластеризация, но настраивается по-разному.

Рассмотрим настройки узла:

Результаты Кластеризации k-means представлены в разделе Интерпретация.

Кластеризация (g-means)

Рассмотрим настройки узла:

Результаты Кластеризации g-means представлены в разделе Интерпретация.

Интерпретация

Для представления результатов используются следующие визуализаторы:

EM Кластеризация

Таблица отражает разбиение входного набора на кластеры и позволяет оценить вероятность принадлежности класса к определенной группе.

Рисунок 5. Разбиение на кластеры.

В каждом кластере получилось примерно равное количество объектов. Алгоритм выделил 3 группы, которые совпадают с количеством исходных классов и примерно равны, что говорит о хорошей работе алгоритма EM кластеризации.

Рисунок 6. Профили кластеров.

Ниже представлены статистические показатели, по которым можно сравнить кластеры:

Рисунок 7. Профили кластеров (сравнение).

Кластеризация k-means

Таблица отражает разбиение входного набора на кластеры и позволяет оценить принадлежность класса к определенной группе.

Рисунок 8. Разбиение на кластеры.

Алгоритм выделил 3 группы, которые совпадают с количеством классов входного набора, однако в каждом кластере получилось сильно различающееся количество объектов. Таким образом, k-means кластеризация получилась менее точна, чем EM.

Рисунок 9. Профили кластеров.

Ниже представлены статистические показатели, по которым можно сравнить кластеры:

Рисунок 10. Профили кластеров (сравнение).

Кластеризация g-means

Таблица отражает разбиение входного набора на кластеры и позволяет оценить принадлежность класса к определенной группе.

Рисунок 11. Разбиение на кластеры.

Алгоритм выделил 2 кластера, которые, во-первых, не совпадают с количеством классов исходного набора, а, во-вторых, получились неравномерными. Таким образом, g-means кластеризация оказалась наименее точной, и ее результаты можно оценить как неудовлетворительные.

Рисунок 12. Профили кластеров.

Ниже представлены статистические показатели, по которым можно сравнить кластеры:

Рисунок 13. Профили кластеров (сравнение).

Читайте также:

  
• Как сделать клавиатуру на айпаде цельной
  
• Как сделать линейку на карте яндекс
  
• Как сделать роуминг на мегафоне
  
• Как сделать обход гугл аккаунта на алкатель
  
• Как сделать развал передних колес пассат б6