Как сделать изображение в изометрической проекции окружностей вписанных в куб
Как начертить окружность в изометрии?
В предыдущем уроке мы попытались разобраться, как построить изометрию. Если с построением плоских линий и форм все понятно, то построение цилиндрических и конусовидных элементов может вызвать дополнительные вопросы. Итак, рассмотрим окружность в изометрии.
Как вы наверняка знаете, при построении изометрии окружность изображается в виде эллипса. Причем вполне конкретного: длина большой оси эллипса AB=1.22*D, а длина малой оси CD=0.71*D (где D - диаметр той самой исходной окружности, которую мы хотим начертить в изометрической проекции). Как начертить эллипс зная длину осей? Об этом я рассказывал в отдельном уроке. Там рассматривалось построение больших эллипсов. Если же исходная окружность имеет диаметр где-то до 60-80 мм, то скорее всего мы сможем начертить ее и без лишних построений, используя 8 опорных точек. Рассмотрим следующий рисунок:
Это фрагмент изометрии детали, полный чертеж которой можно увидеть ниже. Но сейчас мы говорим о построении эллипса в изометрии. На данном рисунке AB - большая ось эллипса (коэффициент 1.22), CD - малая ось (коэффициент 0.71). На рисунке половина короткой оси (ОD) попала в вырезанную четверть и отсутствует - используется полуось СО (не забудьте об этом, когда будете откладывать значения по короткой оси - полуось - имеет длину равную половине короткой оси). Итак, мы уже имеем 4 (3) точки. Теперь отложим по двум оставшимся изометрическим осям точки 1,2,3 и 4 - на расстоянии равном радиусу исходной окружности (таким образом 12=34=D). Через полученные восемь точек уже можно провести достаточно ровный эллипс, либо аккуратно от руки, либо по лекалу.
Для лучшего понимания направления осей эллипсов в зависимости от того, какое направление имеет циллиндр, рассмотрим три разных отверстия в детали, имеющей форму параллелепипеда. Отверстие - тот же цилиндр, только из воздуха :) Но для нас это особого значения не имеет. Полагаю, что ориентируясь на эти примеры вы без труда сможете правильно расположить оси своих эллипсов. Если же обобщить, то получится так: большая ось эллипса перпендикулярна той оси, вокруг которой образован цилиндр (конус).
Надеюсь, этот урок поможет вам окончательно осилить изображение деталей в изометрической проекции, и уж однозначно - не будет проблем с тем чтоб начертить окружность в изометрии.
Вы можете сказать "спасибо!" автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект "White Bird. Чертежи Студентам"
или запишите наш телефон и расскажите о нас своим друзьям - кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки - и кто-то еще сможет освоить черчение.
А вот это - не реклама. Это напоминание, что каждый из нас может сделать. Если хотите - это просьба. Мы действительно им нужны:
Молодцы! Отличный ресурс! Облазила много сайтов посвященных инженерной графике, но объяснения приведенные здесь показались мне самыми доступными. Теперь смогу объяснить все дочери :)
Автор комментария: николай
Дата: 2012-04-14
СПАСИБО!урок очень помог.я уже было собирался "на глаз" чертить.
Автор комментария: Леон
Дата: 2012-05-25
Превосходный сайт! Благодарю авторов этого сайта.
Автор комментария: Аида
Дата: 2012-07-11
черчение не мое, но придется любит, работа такая
Автор комментария: е%лан палыч
Дата: 2012-10-08
все четко е$%ть колотить на%
Автор комментария: константин.
Дата: 2013-03-24
спасибо. вспомнил молодость,чертя для внучки. и это хорошее воспоминание..
Вот и хорошо! Внучка хоть и не сама чертит, но у нее есть, у кого спросить. Поскольку объяснить всем я не могу, то очень положительно отношусь к папам, мамам, бабушкам и дедушкам, которые берут на себя труд по несению света. И если мои статьи в этом им помогают - это хорошо.
Автор комментария: Андрей
Дата: 2013-04-12
Нет подробного описания !
Полагаю, что вы имели ввиду недостаточно описанную технологию построения эллипса, но это уже есть в другом уроке, ссылка на него есть в тексте.
Автор комментария: Дмитрий
Дата: 2016-06-07
Здравствуйте. А как изображается резьба у гайки в изометрии?
Дмитрий, к сожалению картинку приложить не смогу, но на словах скажу, что я во всех чертежах изображал ее в соответствии с обычными правилами отображения резьбы на чертеже. Т.е. если деталь чертится с вырезом четверти, то на внутренних краях разрезов появляется дополнительная тонкая линия, обозначающая резьбу. А если без выреза - то просто неполная эллиптическая дуга в районе фаски (или на торцевой поверхности, если вдруг фаска не вычерчена). Неполность дуги аналогична 3/4 окружности при обозначении резьбы. Не стану утверждать, что так абсолютно верно, но ни одного студенческого чертежа мне еще не завернули с такими резьбами.
Автор комментария: Зоя
Дата: 2016-12-16
Спасибо! Тоже бабушка, несущая свет
Автор комментария: 123
Дата: 2019-03-06
§ 18. Построение аксонометрических проекций плоских фигур и окружностей
Построение аксонометрических проекций плоских фигур и окружностей
Построение аксонометрических проекций мы начнем с построения аксонометрических проекций плоских геометрических фигур. Знание приемов построения плоских фигур (квадрата, треугольника, прямоугольника, круга) необходимо для построения аксонометрических проекций геометрических тел, предметов и т. д.

Плоская фигура — фигура, все точки которой находятся в одной плоскости .
В качестве примера рассмотрим алгоритм построения аксонометрической проекции квадрата. По такому же алгоритму строятся аксонометрические проекции других плоских многоугольников.
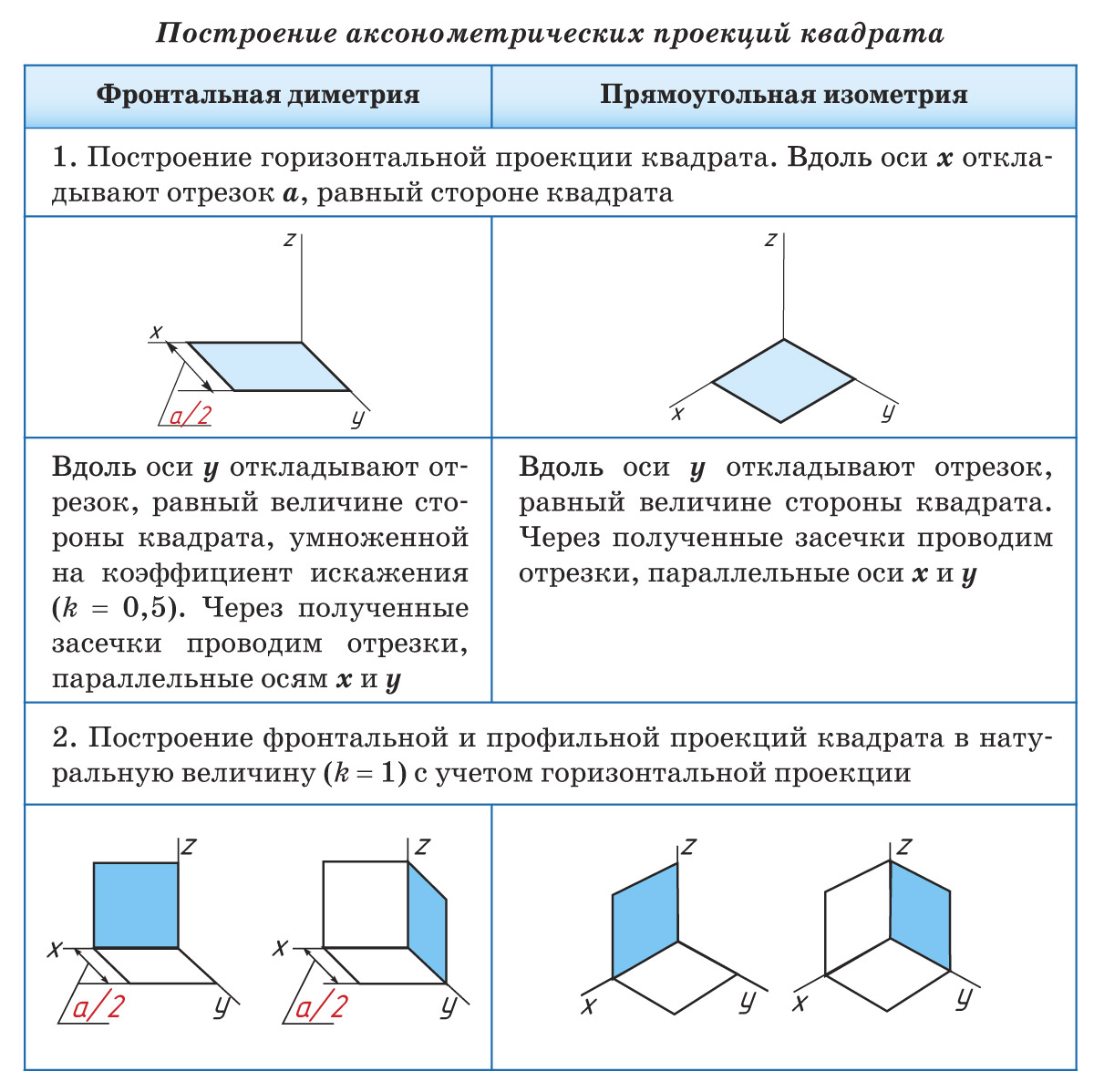
.jpg)
На основе алгоритма построения квадрата постройте аксонометрические проекции прямоугольного треугольника. Какая сторона треугольника будет проецироваться с искажением во фронтальной диметрии?
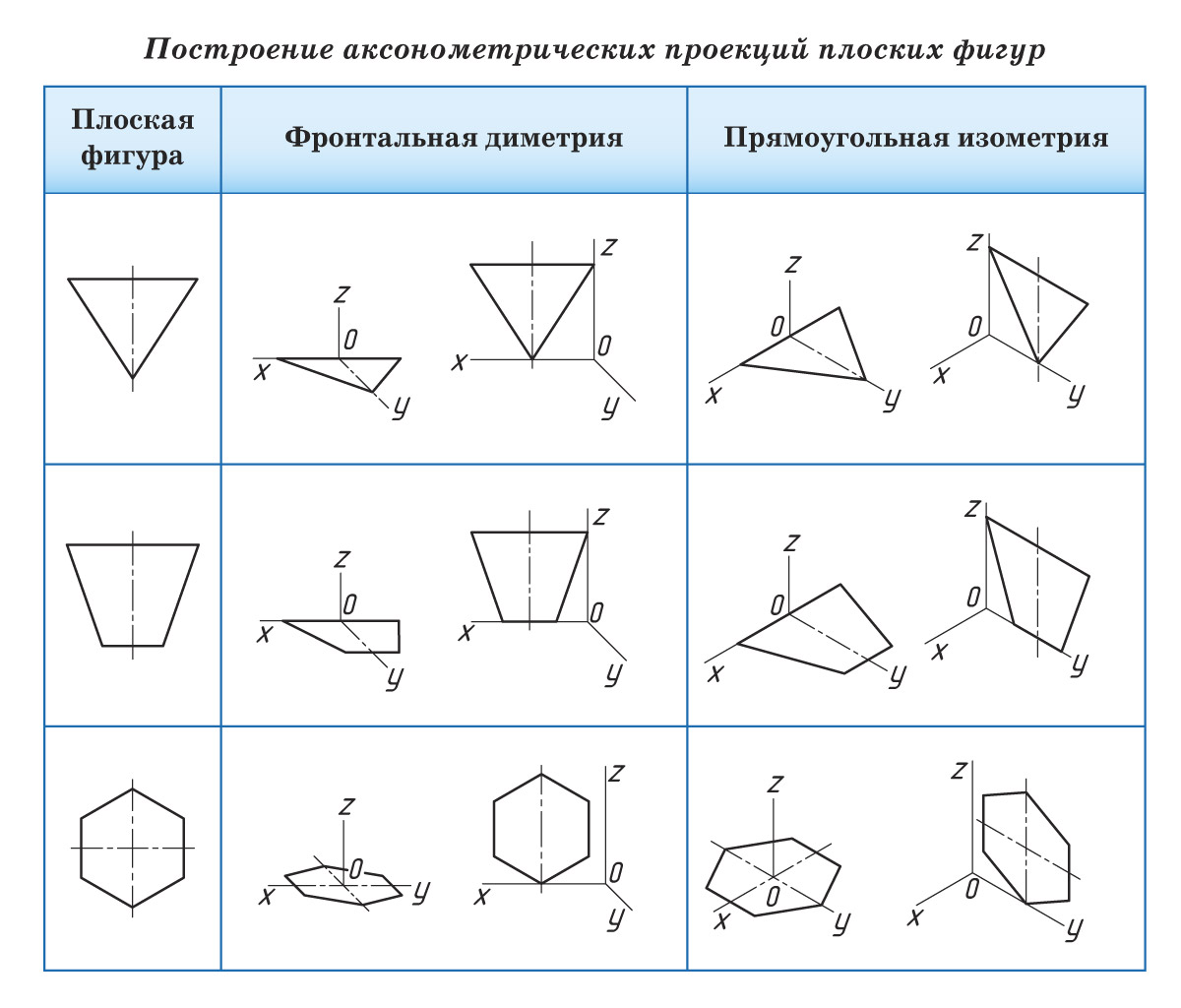

Постройте аксонометрические проекции елки. Какие плоские фигуры составляют изображение? Какой плоскости проецирования елка параллельна?
Кроме многоугольников, к плоским фигурам относят и окружности. В изометрической проекции окружность проецируется в замкнутую кривую линию — эллипс (рис. 55). Для его построения пользуются лекалами, поэтому эллипсы называют лекальными кривыми. Прием построения эллипса сложный и требует длительной работы, поэтому для упрощения построений эллипсы заменяют овалами.

Овал — замкнутая кривая, состоящая из четырех дуг окружностей, плавно переходящих друг в друга (рис. 56).
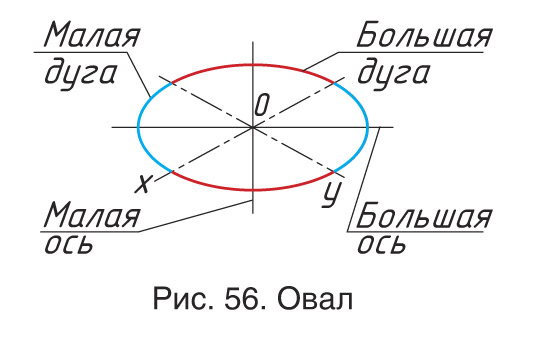
Для удобства построения овала в аксонометрической проекции сначала изображают аксонометрическую проекцию квадрата, построение которой вам уже известно.
Общее построение аксонометрической проекции окружности
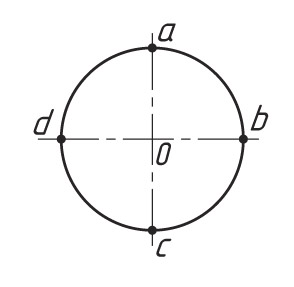
1. Выполняют построение осей аксонометрической проекции. Затем от точки О откладывают отрезки, равные радиусу окружности (R = Oa = Ob = Oc = Od). Через точки а, b, c и d проводят прямые, параллельные осям, получают ромб. Большая ось овала располагается на большой диагонали ромба.
2. Выполняют построение больших дуг овала. Из вершин А и В описывают дуги радиусом R, равные расстоянию от вершины (А или В) до точек a, b, c, d (R = Ad = Bb).
3. Строят малые дуги овала. Через точки B и a, B и b проводят прямые. На пересечении прямых Вa и Вb с большой диагональю ромба находят точки 1 и 2. Они будут центрами малых дуг. Их радиус R1 равен 1а или 2b
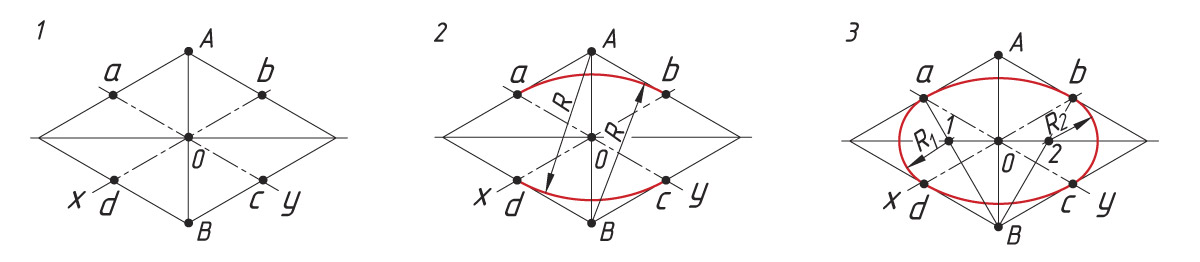
Построение фронтальной и профильной проекций окружности
Фронтальная и профильные проекции окружности выполняются по такому же алгоритму, как и горизонтальная проекция.

Помните! Большая ось овала всегда перпендикулярна аксонометрической оси, не участвующей в образовании плоскости, на которой ведется построение. Малая ось — продолжение аксонометрической оси.

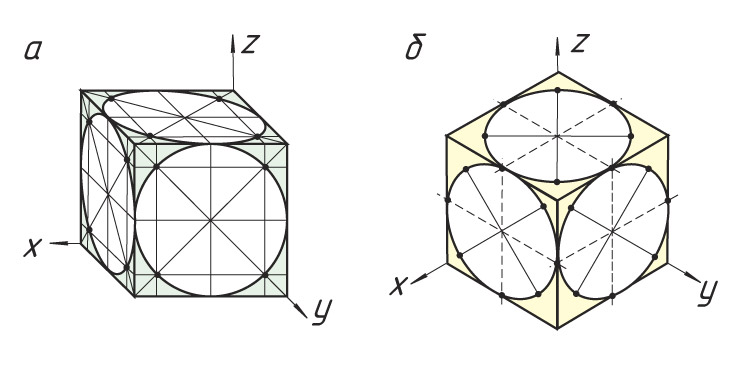
Определите, на каком рисунке (а или б) изображен куб в изометрии. Объясните, как вы это определили.

Эллипсограф, или Сеть Архимеда, — механизм, который способен преобразовывать возвратно-поступательное движение в эллипсоидное. Применяется в качестве чертежного инструмента для вычерчивания эллипсов, а также в качестве приспособления для разрезания стекла, бумаги, картона. История этого механизма точно не определена, но считается, что эллипсографы существовали еще во времена Архимеда.
В первую очередь, необходимо на достаточном для понимания сути уровне разобраться в том, как строить саму изометрию – то есть метрическое плоское пространство. Начинать нужно с самых основ, связанных с работой с изометрическими проекциями и плоскостями. Они включают в себя построение простейших и обычных плоских линий, лишь после освоения которых можно переходить к изучению форм. Вполне естественно, что без знания азов ни у кого не выйдет перескочить сразу к различным цилиндрическим формам, ведь проблема возникнет сразу же на этапе построения таких более сложных по сравнению с линиями фигур, как квадрат, а затем и круг в изометрии. Многие выдвигают такую точку зрения, что именно окружность является одной из наиболее проблематичных для изображения в проекции среди всех плоских фигур.
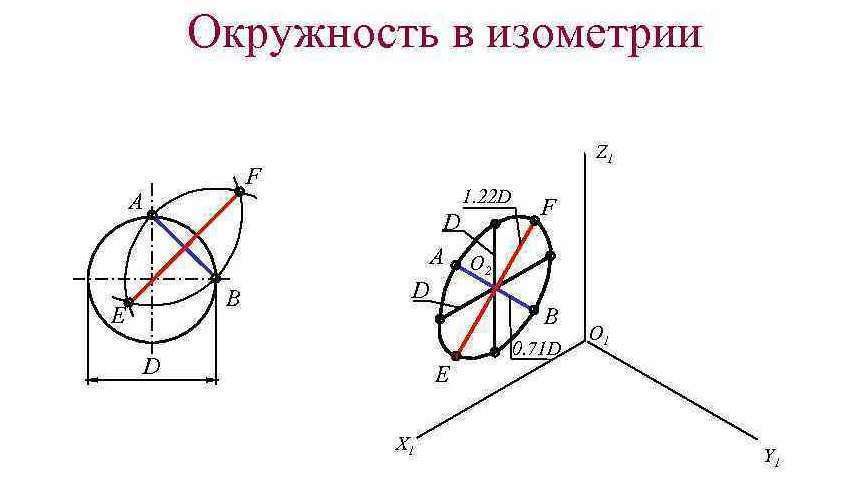
Изображение изометрической проекции
Сама суть проекции состоит в том, что какой-либо существующий трехмерный объект или фигура отображается на изометрической плоскости, при этом сохраняется отношение длины спроектированных отрезков к действительной длине. Другими словами, коэффициент искажения остается неизменным по всем трем осям. Этим и отличается изометрическая проекция, так как только при ней все имеющиеся масштабы остаются одинаковыми.
Изометрическая проекция возможна при соблюдении условия, чтобы углы между осями проекции были одинаковыми и равны 120 градусам. У подобной проекции есть достоинство, благодаря чему ее так часто используют в различных чертежах и проектах. Причина кроется в том, что при изменении расстояния сами отражаемые объекты при этом не кажутся меньше или больше, чем они есть на самом деле.
Однако у изометрических проекций существуют и свои недостатки. Так, например, если на рисунке отсутствуют обозначающие тени на разных сторонах, то будет крайне сложно определить, какая из сторон фигуры на данный момент находится к нам ближе и, собственно, наблюдается. Кроме того, будет проблематично понять, где у объекта располагаются верхняя и нижняя грань, из-за наличия двух крайне схожих проекций, равных по площади и размерам.
Смотрите видео об окружности в изометрии.
Как чертить круг в изометрии?
Все, кто на каком-либо из этапов обучения сталкиваются с вопросом, как начертить круг в изометрии, очень часто совершают типичные и распространенные среди новичков ошибки.
Основные факторы при построении изометрической проекции, которые нужно запомнить, заключаются в нескольких деталях:
- Дело в том, что в случаях вычерчивания в изометрии окружность изображается не в своем первоначальном положении. В конечном итоге она должна принять форму эллипса.
- Вдобавок к этому, есть важный элемент, который задает курс всему последующему построению. Нужно ориентироваться на тот момент, что любую окружность можно рассматривать как правильный многоугольник, в котором может быть неограниченное множество сторон.
Как уже было сказано, в изометрическом пространстве окружность отображается в виде эллипса. Но начинающие регулярно сталкиваются с проблемами, так как он достаточно сложен для построения. В связи с данным фактом часто рекомендуется прибегать к использованию овалов как оптимальной замене эллипсам.
Всего существует несколько инструкций для разных способов, как чертить круг в изометрии через овал. В нашем же случае будет рассмотрен один из наиболее часто используемых и распространенных. Первоочередным этапом является вычисление размеров самих осей фигуры, большой и малой, по формулам через диаметр окружности, изометрическую проекцию которой необходимо вычертить.
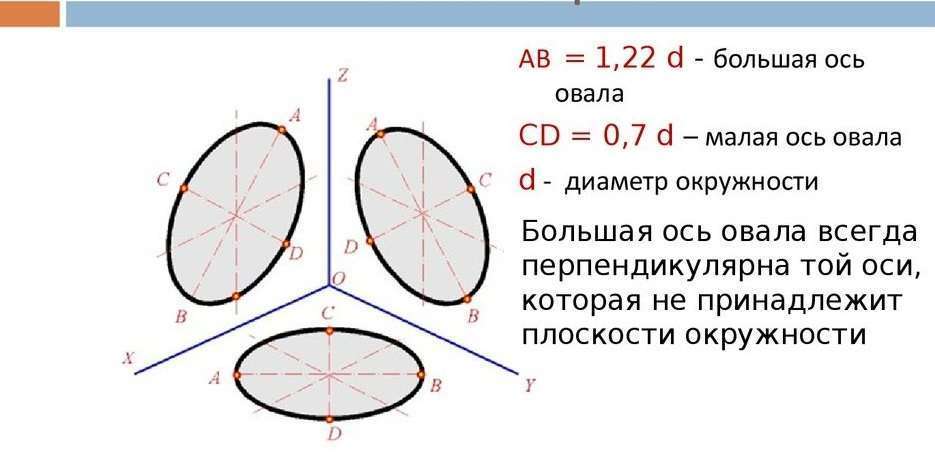
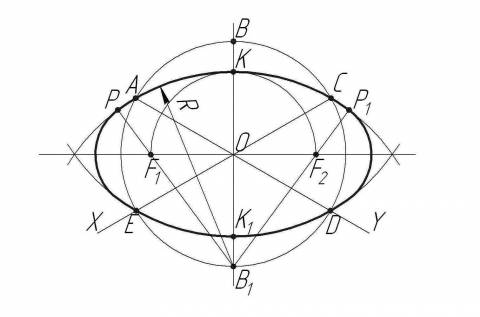
Существует также и графический способ определения осей эллипса, который изучается наглядным путем. Для вычисления малой оси требуется соединить между собой ближайшие точки перпендикулярных прямых линий, проведенных через центр окружности, лежащие на этой самой окружности. Дальше через эти точки проводятся дуги радиусов так, чтобы они пересеклись между собой. Данные точки пересечения будут образовывать линию, которая, в свою очередь, является большой осью.
Круг в изометрии: построение
Руководство, как нарисовать круг в изометрии, не заканчивается на вычислении размеров осей. В зависимости от принадлежности к какой-либо из координатных плоскостей, устанавливается направление вычисленных и построенных ранее осей овала. Следом за этим по размерам обеих осей проводятся окружности. При их пересечении выделяются четыре точки, которые впоследствии послужат центрами дуг необходимого нам овала.
Так как приводимая поэтапная инструкция приводится скорее для новичков, которые только учатся, как сделать круг в изометрии, то следует подробнее рассмотреть процесс определения направления осей вычерчиваемого эллипса. Прежде всего, это зависит непосредственно от положения самой окружности, которую требуется спроецировать.
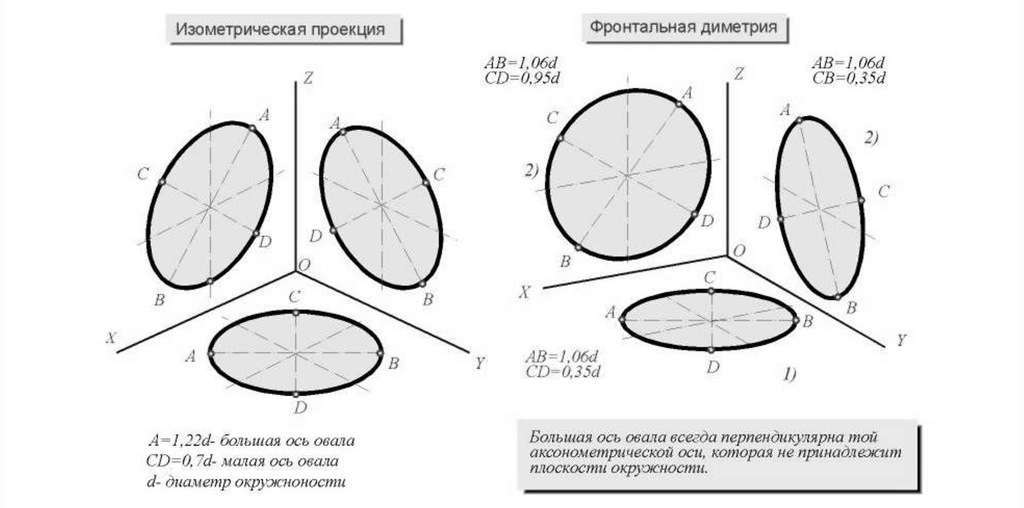
При построении всегда соблюдается одно негласное правило: при любых обстоятельствах большая ось будет расположена перпендикулярно к оси, которая проецируется в точку на данной плоскости. Малая ось при этом обязательно совпадает по направлению с этой осью.
Чтобы впоследствии, после завершения всех расчетов и непосредственного построения проекции, у других людей, не знакомых изначально с вашим чертежом, не возникали трудности с определением сторон, используется нанесение теней и штриховки. При этом очень важным условием является направление имеющихся штрихов. Так, например, принято, что в изометрической проекции линии должны совпадать по своей направленности либо с большими диагоналями квадрата, в который вписана окружность, либо с малыми.
Помимо этого, чтобы в дальнейшем упростить задачу людям, которым предстоит работать по данным чертежам, зачастую на рисунок наносятся еще и тени, отбрасываемые вычерченной проекцией. Это не только сводит к минимуму возникновение недопонимания, но и делает проект в эстетическом плане более приятным для восприятия.
Остались ли у вас вопросы по теме? Задайте их в комментариях! А также смотрите видео о построении изометрии окружности.
изображение в изометрической проекции окружностей вписанных в куб

04:24

03:31

05:41

05:02

02:29
![Oliver Tree & Little Big - The Internet [Music Video]](https://i.ytimg.com/vi/5Og1N-BVSwg/0.jpg)
03:36

04:43
Окружности в изометрии изображаются в виде эллипсов (рис. 6.8) с указанием величин осей эллипсов для приведенных коэффициентов искажения, равных единице.
Большая ось эллипсов расположена под углом 90° для эллипсов, лежащих в плоскости xOz к оси у, в плоскости yOz к оси х, в плоскости xOy к оси z.
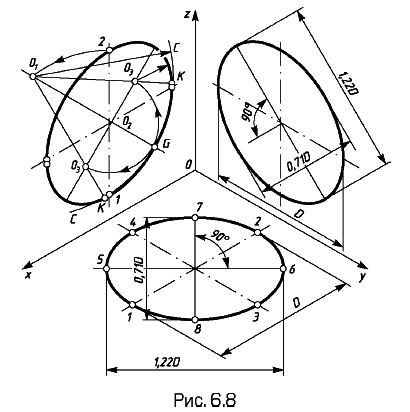
При построении изометрического изображения от руки (как рисунка) эллипс выполняют по восьми точкам. Например, по точкам 1, 2, 3, 4, 5, 6, 7 и 8 (см. рис. 6.8). Точки 1, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей элипса. При вычерчивании эллипсы в изометрической проекции можно заменять овалами и строить их следующим образом 1 . Построение показано на рис. 6.8 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра, делают засечку радиусом R = D на продолжении малой оси эллипса в точке О1 (строят также аналогичным образом и симметричную ей точку, которая на чертеже не показана). Из точки O1 как из центра проводят дугу CGC радиуса D, которая является одной из дуг, составляющих контур эллипса. Из точки О2 как из центра проводят дугу радиуса O2G до пересечения с большой осью эллипса в точках О3. Проводя через точки О1, O3 прямую, находят в пересечении с дугой CGCточку K, которая определяет O3K — величину радиуса замыкающей дуги овала. Точки K являются также точками сопряжения дуг, составляющих овал.
Изометрия цилиндра
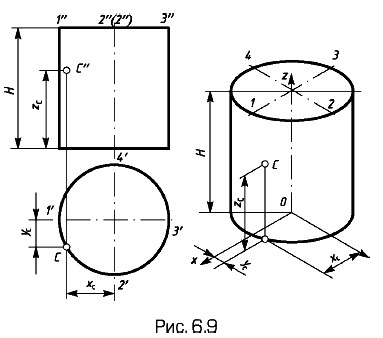
Изометрическое изображение цилиндра определяется изометрическими изображениями окружностей его основания. Построение в изометрии цилиндра высотой Н по ортогональному чертежу (рис. 6.9, слева) и точки С на его боковой поверхности показано на рис. 6.9, справа.
Пример построения в изометрической проекции круглого фланца с четырьмя цилиндрическими отверстиями и одним треугольным приведен на рис. 6.10. При построении осей цилиндрических отверстий, а также ребер треугольного отверстия использованы их координаты, например координаты х и y .

Описание презентации по отдельным слайдам:
Начертательная геометрия Проецирование цилиндра. Построение комплексного чертежа Построение аксонометрической проекции Определение проекций точек на поверхности цилиндра
Построение координатных осей X Z Y Y 0
Построение осей симметрии X Z Y Y 0
Построение основания цилиндра X Z Y Y 0 d
Построение фронтальной и профильной проекции цилиндра X Z Y Y 0 d h
Построение круга в изометрии Точки А- являются центрами больших дуг овала Точки В – это центры малых дуг овала Точки 1,2,3,4-это точки сопряжения A A R=d/2 B B 0 X Y 1 2 3 4
Аксонометрическое изображение цилиндра Z Y X Y 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1
Построение точек на поверхности цилиндра Z Y X Y 0 d Z1 X1 Y1 h h a’ ZA a a″ ZA a A 01 X1 Y1 Z1 01
Построение точек на поверхности цилиндра Z Y X Y 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1 b’ b b″ ZB XB XB b ZB B
Построение точек на поверхности цилиндра Z Y X 0 d Z1 X1 Y1 h h 01 01 X1 Y1 Z1 b’ b b″ ZB XB XB b ZB B (f’) f f″ ZF F
Международная дистанционная олимпиада Осень 2021
Вам будут интересны эти курсы:
Оставьте свой комментарий
В школе в Пермском крае произошла стрельба
Школьников не планируют переводить на удаленку после каникул
Минпросвещения планирует прекратить прием в колледжи по 43 профессиям
Гинцбург анонсировал регистрацию детской вакцины от COVID-19
Минобрнауки работает над изменением подходов к защите диплома
Студенты разработали программу для предупреждения опасного поведения в школах
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Как правильно построить цилиндр в положении лёжа?
1) Сначала намечаем соотношения пропорций и наклон цилиндра.
2) Представляем цилиндр, находящимся внутри описываемой вокруг него коробки.
3) Намечаем основные направляющие в соответствии с законом линейной перспективы (параллельные линии сходятся в одну точку на линии горизонта).
4) Проверяем соотношения и наклоны направляющих в передней и дальней фронтальных плоскостях коробки. Именно сюда мы будем вписывать эллипсы.
5) Находим диагонали в данных плоскостях.
6) Находим вертикальную и горизонтальную оси. Построение напоминает подготовительную разметку для рисования эллипса в горизонтальном положении.
7) Намечаем границы эллипса: он будет слегка искажён в соотношении с осями симметрии. Это нормально, так как плоскость, в которую эллипс вписан, тоже слегка видоизменена, вытянута по диагонали.
8) Дальний эллипс выглядит более “круглым”, по сравнению с передним. Это происходит потому, что пропорции дальней плоскости немного видоизменены по сравнению c ближайшей из-за подчинения направляющих объекта линейной перспективе. Так и должно быть, не пугайтесь, но от сильного искажения лучше избавиться. Как правило, у небольших по размеру объектов искажение едва уловимо глазом.
Если вам хочется ещё лучше научиться рисовать базовые формы, у нас есть для вас:
Смело нажимайте на ссылку.
Если вам понравилась эта статья, сделайте следующее:
2. Поделитесь этим постом с друзьями в социальных сетях или своём блоге.
3. И конечно же, оставьте свой комментарий ниже 🙂
Как начертить цилиндр в изометрии пошагово
§ 14. Построение аксонометрических проекций окружности
Рассмотрите рис. 92. На нем дана фронтальная диметрическая проекция куба с вписанными в его грани окружностями.
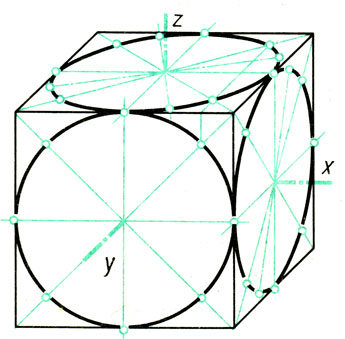
Рис. 92. Фронтальные диметрические проекции окружностей, вписанных в грани куба
Окружности, расположенные на плоскостях, перпендикулярных к осям х и z, изображаются эллипсами. Передняя грань куба, перпендикулярная к оси у, проецируется без искажения, и окружность, расположенная на ней, изображается без искажения, т. е. описывается циркулем. Поэтому фронтальная диметрическая проекция удобна для изображения предметов с криволинейными очертаниями, подооных представленными на рис. 93.
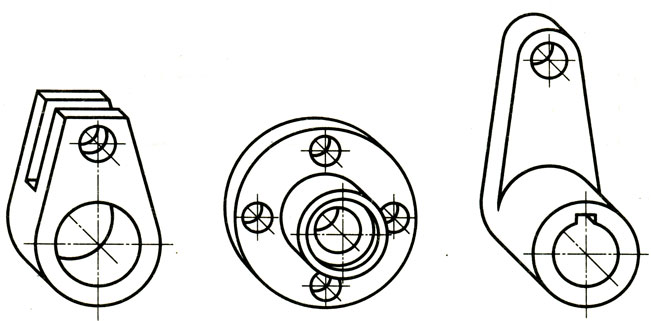
Рис. 93. Фронтальные диметрические проекции деталей
Построение фронтальной диметрической проекции плоской детали с цилиндрическим отверстием. Фронтальную диметрическую проекцию плоской детали с цилиндрическим отверстием выполняют следующим образом.
1. Строят очертания передней грани детали, пользуясь циркулем (рис. 94, а).
2. Через центры окружности и дуг параллельно оси у проводят прямые, на которых откладывают половину толщины детали. Получают центры окружности и дуг, расположенных на задней поверхности детали (рис. 94, б). Из этих центров проводят окружность и дуги, радиусы которых должны быть равны радиусам окружности и дуг передней грани.
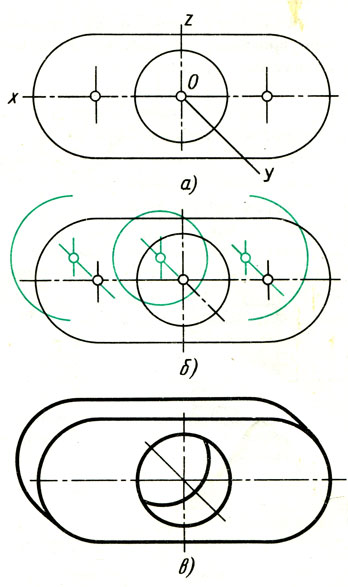
Рис. 94. Построение фронтальной диметрической проекции детали с цилиндрическими элементами
3. Проводят касательные к дугам. Удаляют лишние линии и обводят видимый контур (рис. 94, в).
Изометрические проекции окружностей. Квадрат в изометрической проекции проецируется в ромб. Окружности, вписанные в квадраты, например, расположенные на гранях куба (рис. 95), в изометрической проекции изображаются эллипсами. На практике эллипсы заменяют овалами, которые вычерчивают четырьмя дугами окружностей.
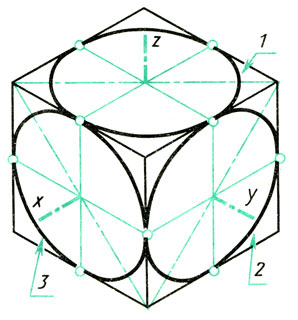
Рис. 95. Изометрические проекции окружностей, вписанных в грани куба
Построение овала, вписанного в ромб.
1. Строят ромб со стороной, равной диаметру изображаемой окружности (рис. 96, а). Для этого через точку О проводят изометрические оси х и у и на них от точки О откладывают отрезки, равные радиусу изображаемой окружности. Через точки a, w, с и d проводят прямые, параллельные осям; получают ромб. Большая ось овала располагается на большой диагонали ромба.
2. Вписывают в ромб овал. Для этого из вершин тупых углов (точек А и В) описывают дуги радиусом R, равным расстоянию от вершины тупого угла (точек А и В) до точек a, b или с, d соответственно. Через точки В и а, В и b проводят прямые (рис. 96, б); пересечение этих прямых с большей диагональю ромба дает точки С и D, которые будут центрами малых дуг; радиус R1 малых дуг равен Са (Db). Дугами этого радиуса сопрягают большие дуги овала. Так строят овал, лежащий в плоскости, перпендикулярной к оси z (овал 1 на рис. 95). Овалы, находящиеся в плоскостях, перпендикулярных к осям х (овал 3) и у (овал 2), строят так же, как овал 1., только построение овала 3 ведут на осях у и z (рис. 97, а), а овала 2 (см. рис. 95) — на осях х и z (рис. 97, б).
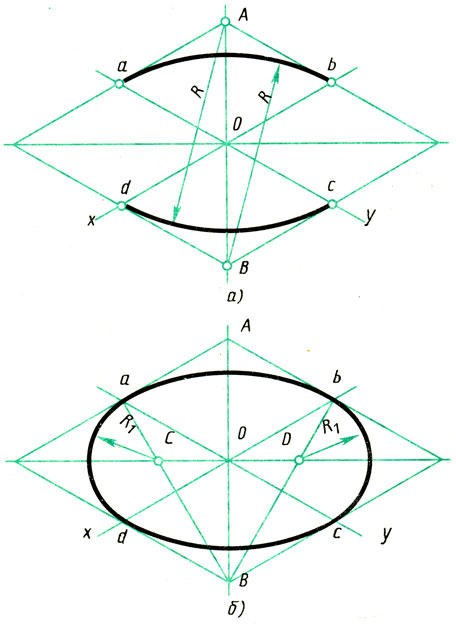
Рис. 96. Построение овала в плоскости, перпендикулярной оси z
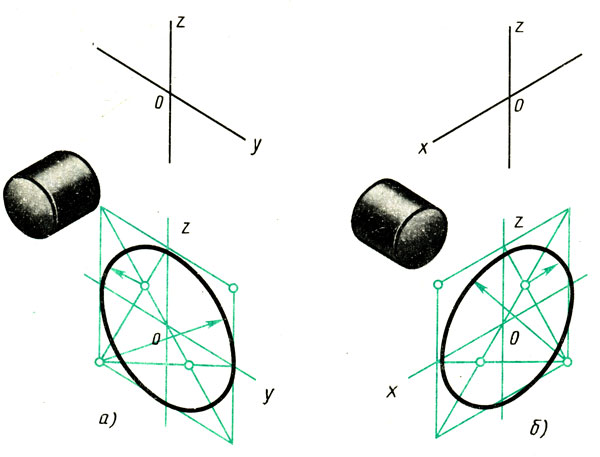
Рис. 97. Построение овала в плоскостях, перпендикулярных осям х и у
Построение изометрической проекции детали с цилиндрическим отверстием.
Как применить рассмотренные построения на практике?
Дана изометрическая проекция детали (рис. 98, а). Нужно изобразить сквозное цилиндрическое отверстие, просверленное перпендикулярно передней грани.
Построения выполняет следующим образом.
1. Находят положение центра отверстия на передней грани детали. Через найденный центр проводят изометрические оси. (Для определения их направления удобно воспользоваться изображением куба на рис. 95.) На осях от центра откладывают отрезки, равные радиусу изображаемой окружности (рис. 98, а).
2. Строят ромб, сторона которого равна диаметру изображаемой окружности; проводят большую диагональ ромба (рис. 98, б).
3. Описывают большие дуги овала; находят центры для малых дуг (рис. 98, в).
4. Проводят малые дуги (рис. 98, г).
5. Строят такой же овал на задней грани детали и проводят касательные к обоим овалам (рис. 98, д).
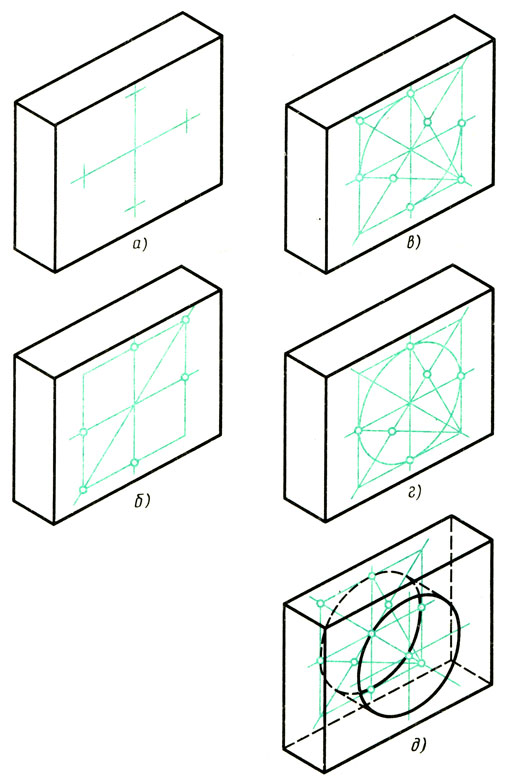
Рис. 98. Построение изометрической проекции летали с цилиндрическим отверстием
Ответьте на вопросы
1. Какими фигурами изображаются во фронтальной диме-трической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х и у?
2. Искажается ли во фронтальной диметрической проекции окружность, если ее плоскость перпендикулярна оси у?
3. При изображении каких деталей удобно применять фронтальную диметрическую проекцию ?
4. Какими фигурами изображаются в изометрической проекции окружности, расположенные на плоскостях, перпендикулярных к осям х, у, z?
5. Какими фигурами в практике заменяют эллипсы, изображающие окружности в изометрической проекции?
6. Из каких элементов состоит овал?
7. Чему равны диаметры окружностей, изображенных овалами, вписанными в ромбы на рис. 95, если стороны этих ромбов равны 40 мм?
Задания к § 13 и 14
Упражнение 42

На рис. 99 проведены оси для построения трех ромбов, изображающих квадраты в изометрической проекции. Рассмотрите рис. 95 и запишите, на какой грани куба — верхней, правой боковой или левой боковой будет расположен каждый ромб, построенный на осях, данных на рис. 99. Какой оси (х, у или z) будет перпендикулярна плоскость каждого ромба?
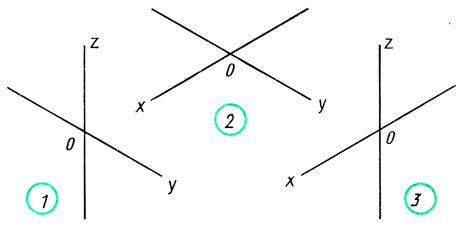
Рис. 99. Задание для упражнений
Упражнение 43

Запишите, какой оси (х, у или z) перпендикулярны плоскости овала на рис. 100. В какой аксонометрической проекции даны здесь окружности?
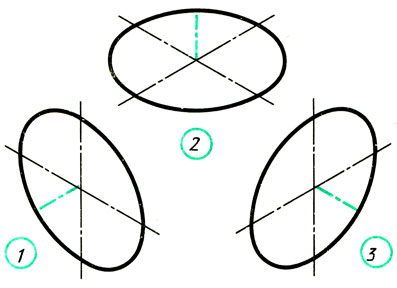
Рис. 100. Задание для упражнений
Упражнение 44

В каких аксонометрических проекциях даны окружности на рис. 101? Какой оси перпендикулярна плоскость каждой из них?
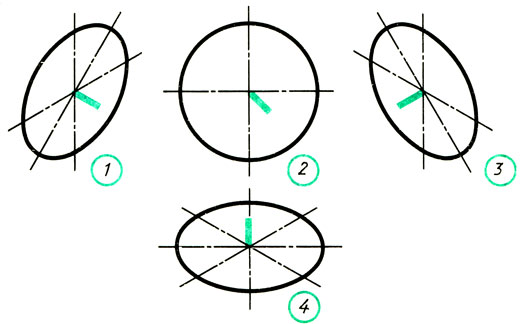
Рис. 101. Задание для упражнений
Упражнение 45

Запишите, в каких аксонометрических проекциях даны геометрические тела на рис. 102.
Каким осям (х, у или z) параллельна высота каждого из них?
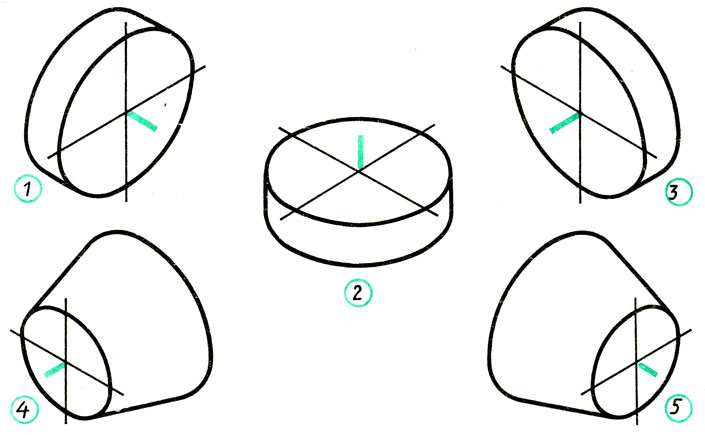
Рис. 102. Геометрические тела для задания для упраждений
Упражнение 46

Постройте изометрическую проекцию куба, сторона которого равна 70 мм. Впишите в три грани куба овалы — изометрические проекции окружностей (см. рис. 95).
Читайте также:


