Как сделать итерации в маткаде
Как решить нелинейное уравнение методами с итерациями (типа половинного деления, Ньютона) ?
Можно ли в маткаде создавать циклы?
Можно последовательно записывать шаги метода безо всяких циклов. Это, кстати, очень наглядно демонстрирует сходимость. Но это сродни ручному просчету.
Вообще-то, в маткаде есть полноценные средства программирования, и циклы там тоже есть, можно запрограммировать любой метод. Но есть один существенный недостаток: программа на маткаде - черный ящик, нет никаких штатных средств отладки этих программ.
Цель лекции заключается в рассмотрении таких
инструментов пакета Mathcad,
которые можно
использовать для решения различного вида
уравнений.
Задачи. Для достижения поставленной цели в
лекции
будут
приведены
теоретические
характеристики данного инструментария и примеры
его практического использования.
Решение нелинейных уравнений
Нелинейные уравнения можно разделить на 2 класса алгебраические
и
трансцендентные.
Алгебраическими
уравнениями
называют
уравнения,
содержащие
только
алгебраические
функции
(целые,
рациональные,
иррациональные). В частности, многочлен является целой
алгебраической функцией. Уравнения, содержащие другие
функции (тригонометрические, показательные, логарифмические и
другие) называются трансцендентными.
Методы решения нелинейных уравнений делятся на две
группы:
точные методы;
итерационные методы.
Точные методы позволяют записать корни в виде некоторого
конечного соотношения (формулы). Из школьного курса алгебры
известны такие методы для решения тригонометрических,
логарифмических,
показательных,
а
также
простейших
алгебраических уравнений.
4. Решение нелинейных уравнений
Как известно, многие уравнения и системы уравнений
не имеют аналитических решений. В первую очередь это
относится к большинству трансцендентных уравнений
Для их решения используются итерационные методы
с заданной степенью точности (не более значения
заданного системной переменной TOL).
5. Решение нелинейных уравнений
Пусть дано уравнение f ( x) = 0, где:
1) Функция f(x) непрерывна на отрезке [a, b] вместе со своими
производными 1-го и 2-го порядка.
2) Значения f(x) на концах отрезка имеют разные знаки (f(a) ⋅ f(b) , и .
Ввести любое выражение, которое включает функцию Find,
например: а:= Find(х, у).
24. Решение систем уравнений
1.
2.
3.
4.
Find(z1, z2, . . .)
возвращает точное решение системы уравнений.
Число аргументов должно быть равно числу
неизвестных.
Ключевое слово Given, уравнения и неравенства,
которые следуют за ним, и какое–либо выражение,
содержащее функцию Find, называют блоком решения
уравнений.
Следующие выражения недопустимы внутри блока
решения:
Ограничения со знаком .
Дискретный аргумент или выражения, содержащие
дискретный аргумент в любой форме.
Неравенства вида a
MathCAD – это система, ориентированная на пользователя, который не обязан знать абсолютно ничего о программировании. Создатели MathCAD изначально поставили перед собой такую задачу, чтобы дать возможность профессионалам – математикам, физикам и инженерам самостоятельно проводить сложные расчеты, не обращаясь за помощью к программистам. Несмотря на блестящее воплощение этих замыслов, выяснилось, что совсем без программирования MathCAD серьезно теряет в своей силе, в основном, из-за недовольства пользователей, знакомых с техникой создания программ.
В очень ранних версиях MathCAD встроенного языка программирования не было. Чтобы применять привычные операции проверки условий и организовывать циклы, приходилось изобретать причудливую смесь из встроенных функций if и until, а также комбинаций ранжированных переменных. Но надо отметить, что использование ранжированных переменных – мощный аппарат MathCAD, похожий на применение циклов в программировании. В подавляющем большинстве случаев намного удобнее организовать циклы с помощью ранжированных, чем заниматься для этого программированием.
И тем не менее встроенный язык программирования MathCADпозволяет решать самые различные, в том числе и довольно сложные, задачи и является серьезным подспорьем для расчетов. Поэтому последние версии MathCAD имеют не очень мощный, но весьма элегантный собственный язык программирования.
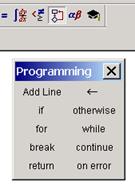
Для вставки программного кода в документы MathCAD имеется специальная панель инструментов. Большинство кнопок этой панели выполнено в виде текстового представления операторов программирования, поэтому их смысл легко понятен. Операторы программирования могут быть введены только с этой панели, но никак не с клавиатуры (можно еще их вводить с помощью сочетаний клавиш, которые приведены в тексте всплывающей подсказки).
Создание программного блока начинается с команды . Нажатие этой клавиши приведет к тому, что в рабочей области документа появится вертикальная черта, а справа от нее – два пустые поля ввода . Вертикальная черта означает, что строки, находящиеся справа от нее, образуют линейную программную последовательность операций. Эта черта является особенностью программ MathCAD. В полях ввода можно ввести две первые строки программы, а если требуется большее число строк, то необходимо нажимать клавишу столько раз, сколько необходимо строк. Не стоит забывать, что программа является полноценным выражением MathCAD. Это выражение может быть использовано для присвоения значения скалярной или векторной переменной или определения функции, или даже в составе другого выражения, в том числе и другой программы.

Для определения функции это будет выглядеть следующим образом:

Последняя строка любой программы не должна содержать никаких управляющих операторов. Эта строка задает значение, возвращаемое программой. В качестве этого значения может быть скаляр (число или переменная), вектор или матрица. Таким образом, последняя строка программы может содержать имя локальной переменной либо некоторое математическое выражение, куда входят как локальные, так и глобальные переменные, либо вектор или матрицу.
Вставить строку программного кода в уже созданную программу можно в любой момент с помощью той же самой кнопки Add Line. Для этого следует поместить на нужное место внутри программы линии ввода.


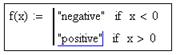



Если вертикальная линия ввода находится в начале текущей строки, то нажатие кнопки приведет к появлению новой строки перед текущей строкой, если вертикальная линия ввода находится в конце строки, то нажатие кнопки приведет к появлению новой строки после текущей. Можно выделить только часть текущей строки, что повлияет на положение новой строки в программе (например, если необходимо для некоторого условия выполнить не одно действие, а несколько). Таким образом, основной принцип создания программных модулей заключается в правильном расположении строк кода. Ориентироваться в их действии довольно легко, т.к. фрагменты кода одного уровня сгруппированы в программе с помощью вертикальных черт.
Проверка условий в программах .
Программы в MathCAD могут быть не только линейными, но и разветвленными. Одним из вариантов ветвления в программах является проверка условия. Условия могут проверять значения как локальных, так и глобальных переменных, а также выражений, содержащих эти переменные.

Если невыполнение условия должно привести к выполнению какого-либо иного программного кода, можно в строке, следующей за оператором if, вставить оператор . В поле ввода слева от этого оператора необходимо ввести строку программы, которая будет выполняться только в том случае, если не выполнилось условие, заданное в операторе if.
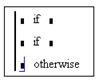
Следует помнить, что если в программе введено подряд несколько строк с оператором if , то выражение слева от оператора otherwise будет выполнено только в том случае, если не выполняются условия, заданные во всех операторах if.
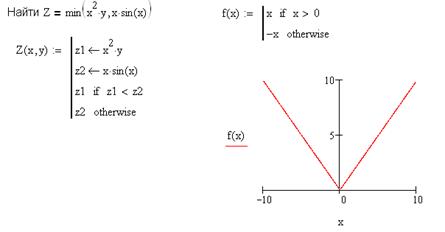
Другим очень важным элементом при создании нелинейных программ являются циклы. Циклы позволяют повторять несколько раз выполнение одного и того же программного блока. Для создания циклов в MathCAD предусмотрено два оператора for и while.
В таких циклах создается некоторая переменная-счетчик, значение которой изменяется после каждого выполнения тела цикла. Выход из цикла происходит при достижении этой переменной заданного значения. Этот оператор вводится с панели Programming клавишей for . В поле ввода после слова for следует указать имя переменной – счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения. В поле ввода после знака следует указать диапазон значений переменной-счетчика. Вводить диапазон в данном случае следует так же, как и при создании ранжированной переменной. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В этом случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Возможность перебора элементов массива не может быть реализована с помощью цикла while, поэтому именно в таких случаях цикл for и является незаменимым. В поле ввода под словом for следует ввести тело цикла.
Пример: Заполнить вектор числами от xнач до xкон с шагом h. Затем определить сумму элементов этого вектора и найти их среднее арифметическое значение.

Цикл while – цикл, который выполняется до тех пор, пока выполняется определенное условие.

В поле ввода справа от слова while следует ввести условие. Это условие строится по тем же правилам, что и в операторе if. Оно будет проверяться после каждого выполнения тела цикла и в тот момент, когда условие перестанет выполняться, повторение тела цикла прекратится. В поле ввода ниже слова while следует ввести тело цикла (напомним, что для ввода нескольких строк в теле цикла надо воспользоваться кнопкой Add Line).
Пример1: Вычислить сумму с точностью е.

Пример2: Найти первый элемент, превышающий определенный порог.
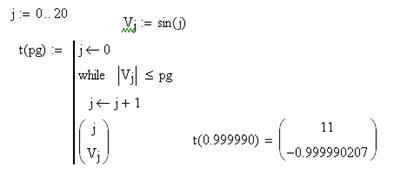
Использование операторов break и continue .
Иногда возникает необходимость повлиять на выполнение цикла некоторым образом, например, прервать его выполнение по какому-либо условию или выполнять некоторые итерации не так, как другие. Для этого и служат операторы break и continue.
Оператор break, если он расположен внутри цикла, означает немедленное прекращение выполнения текущей итерации и выход из цикла. Если есть необходимость прекратить выполнение цикла по какому-либо условию, то следует использовать конструкцию следующего вида break if (условие).
Пример: Выделить из массива все элементы от начала и до первого вхождения в него заданного числа.
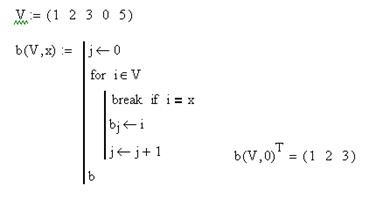
Оператор continue используется для того, чтобы немедленно перейти в начало цикла и начать следующую итерацию. Этот оператор также обычно используется в составе конструкции вида continue if (условие). Оператор continue используется в случаях, когда необходимо чтобы некоторые вычисления производились для одних итераций и не производились для других.
Пример: Требуется заполнить элементы квадратной матрицы в шахматном порядке.

Оператор return (возврат значения) .

Как мы уже указывали, результат выполнения программного модуля помещается, как правило, в последней его строке. Но можно прервать выполнение программы в любой ее точке (например, с помощью условного оператора) и выдать некоторое значение, применив оператор return. В этом случае при выполнении указанного условия значение, введенное в поле ввода после return, возвращается в качестве результата, и никакой другой код больше не выполняется. Вставляется в программу оператор return с помощью одноименной кнопки панели Programming . Пример:

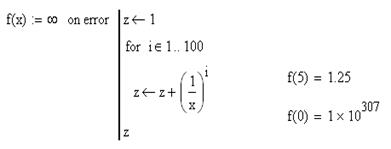
В поле ввода слева может быть введено текстовое выражение, сообщающее об ошибке

Конечно, если программа содержит только простейшие математические операции, то никаких ошибок, кроме деления на нуль или превышения наибольшего допустимого числа в ней возникнуть не может. В таких программах оператор on error используется редко. Но для более сложных программ, которые содержат функции решения дифференциальных уравнений, аппроксимации или другие сложные функции MathCAD, использование on error может избавить от многих трудностей.
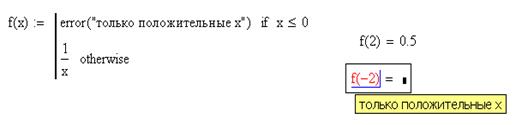
Для того, чтобы иметь возможность нормально вводить текст на русском языке в аргумент функции error (а также во все другие функции со строками), следует изменить шрифт, который используется во встроенном стиле Constant. Для того чтобы этот стиль правильно отображал русские буквы, установите курсор на любом числе или строковом выражении в формульном блоке. При этом в поле на панели инструментов Formatting, отображающем текущий стиль, должно быть написано – Constant. Теперь выберите из раскрывающегося списка шрифтов шрифт, поддерживающий кириллицу.
1. Вычислить функцию sin(x) с точностью е.
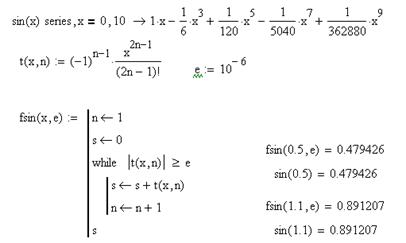
2. Даны массивы А(5) и В(5). Получить массив С, в который записаны сначала элементы
массива А в порядке возрастания, а затем элементы массива В порядке убывания

3. По введенным значениям коэффициентов А, В, С определить корни квадратного уравнения

4. Дан массив натуральных чисел В(10). Определить, есть ли в нем 4 последовательных числа (например, 1, 2, 3, 4, и т.п.). Напечатать такие группы чисел.
Реализуем для некоторого уравнения 4 наиболее популярных численных метода для решения нелинейных уравнений. При этом мы стремимся именно запрограммировать методы, а не воспользоваться встроенным инструментом Given. Find или функциями root , polyroot . Об этих способах решения почитайте, например, здесь.
Определим функцию уравнения f(x)=0 как функцию пользователя, интервал поиска решения зададим переменными a и b . Найти этот интервал можно, например, табличным или графическим методом:
Начальный интервал [a,b] должен быть таким, чтобы значения f(a) и f(b) имели противоположные знаки. Если искомый корень уравнения окажется единственным на интервале, то совсем хорошо 🙂
Логика метода дихотомии (возможно, более правильные названия – метод бисекции, метод половинного деления) довольно проста: если на концах выбранного интервала [a,b] знаки функции совпадают (произведение f(a)*f(b)>0 ), то вернуть результат "недопустимый интервал" (вернём в этом случае ответ "бесконечность"), в противном случае до тех пор, пока длина интервала не станет меньше заданной погрешности ε , будем находить середину текущего интервала c=(a+b)/2 , считать в ней значение функции и проверять, какую из половин отрезка [a,c] или [c,b] нужно отбросить для выполнения следующего шага – а именно, ту, в которой знак f(c) совпадает со знаком функции на левой или правой границе интервала (в листинге – проверка f(a)*f(c)>0 ). Для большей точности вернём середину "последнего" интервала [a,b] , меньшего ε :
В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле xk+1 = φ(xk) , пока не будет достигнута заданная точность |xk+1-xk| . Если выбрать φ(x)=x-c*f(x) , то константу c целесообразнее всего искать методом релаксации, для которого c=2/(M+m) , где M – максимальное из значений первой производной на концах отрезка или в находящихся на нём точках перегиба функции (точках, где f”(x)=0 ), а m – минимальное из таких значений. Вот соответствующий расчёт в MathCAD:
Если заданной сходимости нет в течение 10000 шагов, в подпрограмме предусмотрен аварийный выход.
Численный метод Ньютона решения нелинейного уравнения основан на формуле вида xk+1 = xk-f(xk)/f'(xk) , обеспечивающей наилучшую сходимость, но требующей дополнительного вычисления производной на каждом шаге. Так как производные для MathCAD – не проблема, можно всё сделать "в лоб":
Видно, что сходимость метода – на 2 порядка выше (погрешность найденного решения
Наконец, существует метод хорд, в котором кривая f(x) заменяется прямой линией (хордой), стягивающей точки (a, f(a)) и (b, f(b)) . Формула этого метода зависит от знака выражения f(a)*f”(a) , то есть, имеет два варианта:
Если f(a)*f”(a)>0 , то x =b , xk+1=a-(f(a)(xk-a))/(f(xk)-f(a))
Если f(a)*f”(a) , то x =a , xk+1=xk-(f(xk)*(b-xk))/(f(b)-f(xk))
Вот примерная реализация на MathCAD, как и в предыдущих двух случаях, контролируется максимальное число итераций, равное 10000:
Видно, что сходимость метода оказалась в нашем случае не столь высока.
Подсчитать, сколько шагов какому методу потребовалось, можете сами, немного поменяв выдачу подпрограмм.
05.09.2013, 15:07; рейтинг: 72153
В этом методе нелинейная функция f(x) на отделенном промежутке
[a,b] заменяется хордой, проходящей через точки (a,f(a))и (b,f(b))
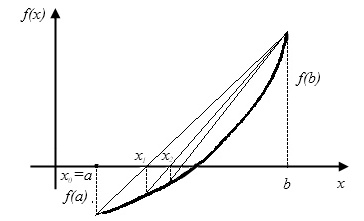
Рис.2.4. Метод хорд. Неподвижен правый конец промежутка b
Уравнение хорды: . Найдем точку пересечения хорды с горизонтальной осью. Полагая и , получим
Точку x1 принимаем за новую границу отрезка, где содержится корень. Через эту точку с координатами (x1,f(x1)) и соответствующую границу предыдущего интервала (b,f(b)) опять проводим хорду, находим и т.д., получая последовательность x1,x2,x3,…xn,…, сходящуюся к корню уравнения.
Вторая производная сохраняет постоянный знак на . Следовательно, возможны два случая. Если f(b)·f "(b)>0, то хорда имеет правый фиксированный конец, причем последовательность x ,x1,…xn приближается к корню слева. За начальное приближение x , естественно, берут a
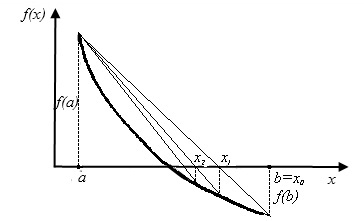
Рис.2.5. Метод хорд. Неподвижен левый конец промежутка a
Если f(a)·f "(a)>0, то хорда имеет левый фиксированный конец, причем последовательность x ,x1,…xn … приближается к корню справа. За начальное приближение x , берут b
Для оценки точности можно воспользоваться формулой
где -точный корень, – приближенный корень, , на промежутке [a,b]. Считаем до тех пор пока, не выполнится условие . Если имеет место неравенство , то счет можно прекратить, когда.
Пример 2.4. Найти методом хорд корень уравнения x 4 -x-1=0
Решение находим, используя пакет Mathcad.
Функция монотонна на промежутках (-∞, 0.63), (0.63, ∞) и меняет на концах промежутков знак. Уравнение имеет два корня. Сузим промежутки отделения корней методом проб, т.е. подстановкой.
Первый корень принадлежит промежутку (-1,-0.5)
Второй корень принадлежит промежутку (1,1.5)
Будем находить корень на промежутке (-1,-0.5)
Вторая производная всюду положительна, функция положительна в точке a = -1, значит, этот конец неподвижен.
| -максимальное, a -минимальное значение модуля производной на промежутке |
так как , множитель
нужно учитывать при оценке точности решения,
Нашли корень исходного уравнения с точностью .
Рис. 2.6. Вычисления в Mathcad, реализующие метод хорд для примера 2.4
2.2.3. Метод Ньютона – метод касательных
Пусть – корень уравнения отделен на отрезке , причем и непрерывны и сохраняют определенные знаки на этом же отрезке . Найдя какое-нибудь n-е значение корня ( ), уточним его по методу Ньютона. Для этого положим , где – считаем малой величиной. Разложим функцию f(x) в ряд Тейлора в окрестности точки x n по степеням h n . Тогда можно записать:
Ограничимся двумя членами ряда и так как , то:
Учитывая найденную поправку hn:,получим (n=0,1,2,…).
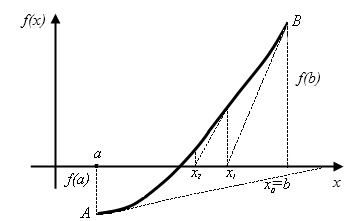
Рис.2.7 Метод касательных. Начальное приближение x =b
По-другому этот метод называется методом касательных. Если в точке провести касательную к функции f(x) , то ее пересечение с осью ОХ и будет новым приближением x1 корня уравнения
Хорошим начальным приближением является то значение, для которого выполнено неравенство . Погрешность вычислений Счет можно прекратить, когда
Теорема 2.2: Если , причем и отличны от нуля и сохраняют определенные знаки при , то, исходя из начального приближения , удовлетворяющего условию , можно вычислить методом Ньютона единственный корень уравнения с любой степенью точности.
Пример 2.5. Найти методом Ньютона корень уравнения x 4 -x-1=0,
| 1-я производная |
| 2-я производная положительна |
| один корень лежит на промежутке (-1.-0.5), второй на промежутке (1.1.5) Уточним левый корень методом Ньютона |
Нашли корень исходного уравнения -0.7245 с точность 0.00007.
Рис. 2.8. Вычисления в Mathcad, реализующие метод касательных для примера 2.5
Численные методы решения нелинейных уравнений. Метод хорд.
Метод хорд ( метод также известен как Метод секущих ) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность .
В отличие от метода половинного деления, метод хорд предлагает, что деление рассматриваемого интервала будет выполняться не в его середине, а в точке пересечения хорды с осью абсцисс (ось – Х). Следует отметить, что под хордой понимается отрезок, который проведен через точки рассматриваемой функции по концам рассматриваемого интервала. Рассматриваемый метод обеспечивает более быстрое нахождение корня, чем метод половинного деления, при условии задания одинакового рассматриваемого интервала.
Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки и (см. рис.1.).


Рис.1. Построение отрезка (хорды) к функции .
Уравнение прямой (хорды), которая проходит через точки А и В имеет следующий вид:

Данное уравнение является типовым уравнением для описания прямой вы декартовой системе координат. Наклон кривой задается по ординате и абсциссе с помощью значений в знаменателе и , соответственно.

Для точки пресечения прямой с осью абсцисс записанное выше уравнение перепишется в следующем виде:

В качестве нового интервала для прохождения итерационного процесса выбираем один из двух или , на концах которого функция принимает значения разных знаков. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
или .
Итерационный процесс уточнения корня заканчивается, когда условие близости двух последовательных приближений станет меньше заданной точности, т.е.

.

Рис.2. Пояснение к определению погрешности расчета.
Следует отметить, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Алгоритм нахождения корня нелинейного уравнения по методу хорд
1. Найти начальный интервал неопределенности одним из методов отделения корней. З адать погрешность расчета (малое положительное число ) и начальный шаг итерации ( ) .
2. Найти точку пересечения хорды с осью абсцисс:

3. Необходимо найти значение функции в точках , и . Далее необходимо проверить два условия:
– если выполняется условие , то искомый корень находится внутри левого отрезка положить , ;
– если выполняется условие , то искомый корень находится внутри правого отрезка принять , .
В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:

4. Проверяем приближенное значение корня уравнения на предмет заданной точности, в случае:

– если разность двух последовательных приближений станет меньше заданной точности , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:

– если разность двух последовательных приближений не достигает необходимой точности , то необходимо продолжить итерационный процесс и перейти к п.2 рассматриваемого алгоритма.
В качестве примера, рассмотрим решение нелинейного уравнения методом хорд. Корень необходимо найти в рассматриваемом диапазоне с точностью .
Вариант решения нелинейного уравнения в программном комплексе MathCAD .

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага итерации представлены в графической форме (см. рис.1).

Рис.1. Результаты расчета по методу хорд
Для обеспечения заданной точности при поиске уравнения в диапазоне необходимо выполнить 6 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: .
Примечание:
Модификацией данного метода является метод ложного положения ( False Position Method ), который отличается от метода секущих только тем, что всякий раз берутся не последние 2 точки, а те точки, которые находятся вокруг корня.
Следует отметить, что в случае если от нелинейной функции можно взять вторую производную алгоритм поиска может быть упрощен. Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:
Из первого условия получается, что неподвижной стороной отрезка является – сторона a .
Из второго условия получается, что неподвижной стороной отрезка является – сторона b .
В общем виде, для выявления неподвижного конца можно записать следующее условие: 0" w /> , где или .

Рис. 3. Примеры убывающей или возрастающей функции
Таким образом, в зависимости от вида функции получаются два выражения для упрощения поиска корня функции:
– если функция соответствует первому случаю (см. рис. 3), тогда формула будет иметь следующий вид:


, где k =0,1,2,…
– если функция соответствует второму случаю (см. рис. 3), тогда формула будет иметь следующий вид:


, где k =0,1,2,…
Случай сводится к рассматриваемому , если уравнение записать в форме: .
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Читайте также:


