Как сделать фрактал
Сейчас придумано большое число алгоритмов рисования фракталов. В интернете можно найти и скачать готовые программы. Но обладателю даже не очень мощного компьютера не составит большого труда нарисовать фрактал Жюлиа, Мандельброта, Галлея или Ньютона в достаточно хорошем качестве своими руками. Опишем в общих чертах процедуру рисования множества Жюлиа многочлена z 2 + c для конкретного значения комплексного параметра c = p + iq.
Для каждой точки z0 = (x0; y0) экрана (то есть центра соответствующего прямоугольника) нужно в цикле последовательно вычислять zk+1 по zk, используя формулу (в координатах это выглядит так: , yk+1 = 2xkyk + q). Признаком остановки цикла является выполнение одного из двух условий: либо на k-м шаге точка zk вышла из круга D (то есть верно неравенство , и тогда точку z0 нужно покрасить в цвет номер k, либо оказалось, что k = K + 1, тогда мы считаем, что точка z0 лежит внутри множества Жюлиа, и красим ее в черный.
В результате работы программы на экран будет выведена квадратная область комплексной плоскости <|Re z| ≤ 1,5, |Im z| ≤ 1,5>, на которой черным цветом будет изображено множество Жюлиа многочлена z 2 + c для выбранного параметра c = p + iq, а остальные точки будут раскрашены в K цветов.
Увеличивая числа a и b, можно повышать разрешение экрана и тем самым улучшать качество изображения. Меняя K и подбирая соответствие между цветами и их номерами, можно добиться довольно красивых картинок.
Это — самая простая процедура построения множества Жюлиа. В программах, которые легко найти и скачать в интернете, используются более сложные алгоритмы рисования. Но в основе большинства из них лежит этот.
В этой статье мы узнаем что такое фракталы и как рисовать их на PHP используя GTK и Cairo.
Немного о фракталах. Интересные факты
Галактики, рельефы планет, океанские волны, облака и молнии, реки, формы растений и животных, и даже человеческое тело можно рассматривать как фракталы…
Библиотека векторной графики Cairo
Итак, мы начинаем рассмотрение основ фрактальной графики на PHP. В нашей работе мы будем использовать графическую библиотеку Cairo , предназначенную для отрисовки векторной графики. Эта библиотека написана на языке C и может быть использована в связке с такими языками как C++, Python и др.
Данная библиотека обладает тремя существенными преимуществами, обеспечивающими её популярность в среде open source:
- открытый исходный код
- переносимость графического кода между различными платформами
- качественная отрисовка векторной графики
Мы так же будем использовать фреймворк GTK , чтобы иметь возможность взаимодействовать с нашим кодом через графический интерфейс и просматривать получившиеся изображения.
Создание окна GTK. Подготовительный этап
Для начала нам придётся создать класс, который будет отвечать за создание окна. Мы назовём его FractalDrawingWindow и унаследуем его от базового класса GtkWindow , который входит во фреймворк GTK. Это позволит нам работать с оконной системой нашей операционной системы и отображать сгенерированные изображения фракталов внутри неё.
abstract class FractalDrawingWindow extends GtkWindow
// глубина рекурсии создаваемого фрактального изображения (по умолчанию)
protected $recursionDepth = 5;
public function FractalDrawingWindow()
parent::__construct(); // здесь мы вызываем конструктор базового класса,
// для успешной инициализации окна
$this->set_title($this->getName()); // устанавливаем название окна
// по имени фрактала
// устанавливаем корректный способ выхода из окна
$this->connect_simple('destroy', array('gtk', 'main_quit'));
$drawingArea = new GtkDrawingArea(); // создаём область для рисования
// устанавливаем функцию отображения фрактала для данной области рисования
// добавляем созданную область в наше окно
// устанавливаем размер окна
$this->set_default_size(640,480); // по ширине и высоте
// устанавливаем позицию окна на экране
// включаем отображение окна
$this->show_all(); // здесь начинается запуск алгоритма отрисовки
// и отображения фрактала
// функция экспозиции фрактала
public function onExpose($darea, $event)
$context = $darea->window->cairo_create(); // создаём Cairo-контекст для отрисовки
$this->onDraw($context); // отрисовываем конкретный вид фрактала
// функция установа глубины рекурсии
public function setRecursionDepth($recursionDepth)
// здесь мы ограничиваем глубину рекурсии для избежания segmentation fault
if($recursionDepth >= 0 && $recursionDepth
// мы используем чистые абстрактные методы, чтобы
abstract public function getName(); // определить названия фракталов
abstract protected function onDraw($context); // и методы их отрисовки
Рисуем фракталы с помощью PHP и Cairo
Теперь мы можем приступать к рассмотрению конкретных видов фракталов и способов их рисования. И начнём мы с фрактала, который получил название в честь немецкого математика, Георга Кантора.
Канторова пыль
Ashes to ashes, dust to dust
Фраза из английской похоронной службы, часто используемая для обозначения фатальной неизбежности конца.
Рассмотрим следующий код:
include 'drawing_window.php'; // здесь мы подключаем файл с ранее созданным
// классом для работы с окнами GTK
// мы создаём класс по конкретному виду фрактала и унаследуем его от класса
// FractalDrawingWindow, капсулирующего функции для работы с оконной системой
class CantorDust extends FractalDrawingWindow
// здесь мы определяем функцию, которая будет отображаться в названии окна
public function getName()
return "Cantor dust fractal";
// здесь мы определяем метод отрисовки фрактала
protected function onDraw($context)
// устанавливаем основной цвет для отрисовки
$context->setSourceRgb(0.5, 0.5, 0.5);
// запускаем рекурсивную функцию отрисовки фрактала "Канторова пыль"
$this->draw($context,$this->recursionDepth, 0, 0, $this->get_size()[0], floatval($this->get_size()[1]) / $this->recursionDepth);
// рекурсивная функция отрисовки
public function draw($context,$level, $posX, $posY, $sizeX, $sizeY)
// в параметрах мы передаём начальные позиции по оси X и Y и размеры элементов для каждого шага рекурсии
// по достижении установленной глубины рекурсии, производим выход из функции отрисовки
// вычисляем новый размер и положение элемента по оси X
$newSizeX = $sizeX / 3;
$newPosX = $posX + 2 * $newSizeX;
// рисуем левый прямоугольник
$context->rectangle($posX,$posY,$newSizeX,$sizeY); // устанавливаем параметры
$context->fill(); // делаем заливку выделенным цветом, уставновленным ранее в методе onDraw()
// рисуем правый прямоугольник
$context->rectangle($newPosX,$posY,$newSizeX,$sizeY);
// запускаем отрисовку следующего уровня рекурсии
$this->draw($context, $level - 1, $posX, $posY + $sizeY, $newSizeX, $sizeY); // слева
$this->draw($context, $level - 1, $newPosX, $posY + $sizeY, $newSizeX, $sizeY); // и справа
$fractal = new CantorDust(); // создаём объект класса для нашего фрактала
$fractal->setRecursionDepth(15); // устанавливаем глубину рекурсии
Gtk::main(); // запускаем наш фреймворк в работу
После запуска этого кода мы увидим что-то вроде:
Здесь мы используем свойство рекурсии, о котором мы говорили ранее в предыдущих статьях . Это свойство позволяет сделать наш код наглядным и простым и сфокусироваться на самой отрисовке. Алгоритм отрисовки достаточно прост: мы берём точку слева и рисуем прямоугольник в треть длины всего отрезка сверху, а затем берём точку справа и рисуем такой же отрезок, и после повторяем эту операцию для левой и правой части, погружаясь на всё глубже по уровню рекурсии.
Для того, чтобы нарисовать прямоугольник, нам достаточно всего трёх методов вызываемых из объекта Сairo-context — это:
- rectangle — устанавливающий параметры прямоугольника,
- fill — производящий заливку цветом,
- а так же setSourceRgb — определяющий цвет заливки.
Вообще существует большущий список методов для работы с Cairo-context, так что предлагаю ознакомиться с ним самостоятельно. В дальнейшем мы будем использовать методы из этого списка для отрисовки всё более сложных и красивых фракталов.
Ура, теперь можно сделать перерыв и выпить чашечку чая! Только что мы разобрались в том, как рисовать простейший фрактал используя PHP и Cairo!
Теперь рассмотрим пример посложнее.
Дерево Пифагора
"Пифагоровы штаны на все стороны равны. Чтобы это доказать, нужно снять и показать"
Народное творчество
Этот фрактал придумал немецкий учитель математики Альберт Босман в 1942 году и назвал его в честь древнегреческого математика Пифагора, потому как каждый уровень этого фрактала содержит фигуры, которые традиционно используются для доказательства теоремы Пифагора: три соприкасающихся квадрата, содержащих между собой прямоугольный треугольник.
Построение данного фрактала начинается с квадрата, над которым строятся ещё два квадрата, уменьшенных на величину √2/2, попарно соединённых между собой общими углами. В классическом случае, угол между двумя квадратами близлежащих уровней составляет 45°, тогда как существуют различные вариации данного фрактала:
- обнажённое дерево Пифагора — каждый квадрат заменяется отрезком
- обдуваемое ветром дерево Пифагора — углы слева и справа отличаются от 45°
- обдуваемое ветром обнажённое дерево Пифагора — сочетаются первые два пункта
Мы же рассмотрим дерево Пифагора в классическом варианте. Вот его код:
include 'drawing_window.php'; // как и ранее мы подключаем класс FractalDrawingWindow
// от которого мы унаследуем методы для работы с оконной системой
class PythagorianTree extends FractalDrawingWindow
// определим метод для отображения имени фрактала в заголовке окна
public function getName()
return "Pythagorian tree fractal";
// и метод для отрисовки самого фрактала
protected function onDraw($context)
$context->setSourceRgb(0.4, 0.9, 0.4); // определим базовый цвет отрисовки
// запустим рекурсивную функцию отрисовки нашего фрактала
$this->draw($context, $this->recursionDepth, $this->get_size()[0]/2 - 50, $this->get_size()[1], $this->get_size()[0]/2 +50, $this->get_size()[1]);
// рекурсивная функция отрисовки
public function draw($context, $depth, $x1, $y1, $x2, $y2)
// производим ограничение на глубину рекурсии
// вычисляем относительные смещения точек квадрата по осям X и Y
// изменяем координаты точек квадрата на данном уровне рекурсии
$x5 = $x4 + floatval(($dx - $dy))*0.5;
$y5 = $y4 - floatval(($dx + $dy))*0.5;
$context->MoveTo($x1, $y1); // смещаемся к координате (x1,y1) это первая точка
$context->LineTo($x2, $y2); // создаём отрезок из точки (x1,y1) к точке (x2,y2)
$context->LineTo($x3, $y3); // и т.д.
$context->LineTo($x4, $y4); // до последней вычисленной точки
$context->closePath(); // закрываем линию возвращаясь в исходную точку (x1,y1)
// устанавливаем цвет на новом уровне рекурсии
$context->setSourceRgb(1.0 - floatval($this->recursionDepth-$depth)/$this->recursionDepth, floatval($this->recursionDepth-$depth)/$this->recursionDepth, 0.0);
// делаем заливку цветом
$depth--; // декрементируем счётчик уровня рекурсии
$this->draw($context, $depth, $x4, $y4, $x5, $y5); // рисуем квадрат слева
$this->draw($context, $depth, $x5, $y5, $x3, $y3); // рисуем квадрат справа от исходного
$fractal = new PythagorianTree(); // создание объекта окна GTK с фракталом
$fractal->setRecursionDepth(10); // установ уровня рекурсии
Gtk::main(); // запуск фреймворка
Чудесно! Теперь мы видим, что можно создавать достаточно сложные фигуры сравнительно простыми методами, используя свойства рекурсии и графические примитивы библиотеки Cairo!
Здесь мы используем несколько иную технику для отрисовки прямоугольников, нежели чем в предыдущем примере. Сочетание функций moveTo , lineTo и closePath позволяет нам строить любые замкнутые многогранники. Заливка цветом при этом ничем не отличается от предыдущего случая. Мы так же указываем значения интенсивности для красного R, зелёного G и синего B каналов, передавая их в качестве параметров в функцию setSourceRgb, а затем вызываем функцию fill .
Ну и напоследок я хотел бы рассмотреть следующий фрактал.
Дракон Хартера — Хейтуэя
Итак, рассмотрим следующий код:
class DragonCurve extends FractalDrawingWindow
public function getName()
return "Dragon curve fractal";
protected function onDraw($context)
// здесь в отличие от предыдущих двух случаев мы используем итеративный метод
// создания последовательности операций отрисовки
$startAngle = -$this->recursionDepth * 3.14 / 4;
$side = 400 / pow(2, $this->recursionDepth / 2.);
$this->draw($context, $turns, $startAngle, $side, $this->get_size()[0]/2, $this->get_size()[1]/2);
// метод получения последовательности операций отрисовки дракона Хартера
public function getSequence($depth)
$seq = array(); // создаём исходный пустой массив
$copy = $seq; // создаём копию данного массива
$copy = array_reverse($copy); // инвертируем порядок элементов массива на инверсный (элементы в начале перемещаются в конец и наоборот)
// добавляем к исходному массиву код направления угла поворота линии для данного фрактала
// добавляем к исходному массиву реверсную копию инвертированных направлений углов поворота с предыдущего уровня итерации
foreach($copy as $val)
// возвращаем последовательность направлений углов поворота линий данного фрактала
// определяем функцию отрисовки для полученной последовательности направлений
public function draw($context, $turns, $startAngle, $side, $x1, $y1)
$angle = $startAngle; // устанавливаем начальный угол
$x2 = $x1 + intval(cos($angle)*$side); // производим поворот исходной точки
$y2 = $y1 + intval(sin($angle)*$side);
$context->setSourceRgb(0.4, 0.4, 0.9); // устанавливаем исходный цвет линии
// переходим к точке x1,y1
// строим отрезок к точке x2,y2
// переходим к следующей точке
foreach($turns as $turn)
$angle += $turn * 3.14 / 2; // изменяем угол поворота на 90 градусов в соответствии
// с рассчитанной заранее последовательностью
// производим поворот и отрисовку фигуры на новом уровне итерации
$x2 = $x1 + intval(cos($angle)*$side);
$y2 = $y1 + intval(sin($angle)*$side);
$fractal = new DragonCurve();
На выходе нашей программы мы увидим следующее изображение:
Закон Мёрфи призван для того, чтобы исключить всякую возможность подобного сценария. В мире программирования он выполняет очень важную роль, и его нужно всегда учитывать. И особенно его нужно учитывать, когда разрабатываемое программное обеспечение выполняет функции управления сложной техникой, от которой зависят человеческие жизни. На практике это означает более тщательный подход к разработке и тестированию программ.
В нашей статье мы рассмотрели различные виды плоских фракталов и способы их отрисовки с помощью графической библиотеки Cairo и фреймворка GTK на PHP. На этом тема фракталов и векторной графики не заканчивается. И мы более подробно раскроем её в следующей статье, которая будет посвящена фрактальной геометрии природы и грамматикам Линденмайера.
В этой статье приведены примеры расчета и построения графической интерпретации некоторых алгебраических и геометрических фракталов.
Фракталы можно разделить на несколько видов:
- Геометрические фракталы – строятся на основе исходной фигуры (линии, многоугольника или многогранника) путем ее дробления и выполнения различных преобразований полученных фрагментов.
- Алгебраические фракталы – строятся на основе алгебраических формул.
- Стохастические фракталы – получаются, если в итерационном процессе случайным образом изменять какие-либо параметры.
Фракталы нашли применение в физике (моделирование сложных процессов и материалов), биологии (моделирование популяций, описание сложных ветвящихся структур), технике (фрактальные антенны), экономике. Существуют алгоритмы сжатия изображений с помощью фракталов. В компьютерной графике фракталы используются для построения изображений природных объектов – растений, ландшафтов, поверхности морей и т. д.
Некоторые примеры алгебраических и геометрических фракталов
Фрактал Мандельброта
Рассмотрим последовательность комплексных чисел:
\[z_ = z_k^2 + c, k = 0, 1, 2, \dots, z_0 = c\]
Множество точек c, для которого эта последовательность не расходится, называется множеством Мандельброта. Для построения его графической интерпретации нужно определить исходные данные:
- прямоугольное окно C с разрешением \(m \times n\) точек;
- значение \(r_ = 2\) – минимальный радиус расходимости множества Мандельброта
- максимальное число итераций \(k_\max\)
Если точка \(z_k\) вышла за пределы круга радиуса \(r_\min\) при \(k \lt k_\max\), то процесс вычисления останавливается.
Построение: для каждой точки \(c_ \in C (i = \overline, j = \overline, c_x \in [-2; 1], c_y \in [-2; 1,5])\) запустим итерационный процесс:
\[x_ = x_k^2 - y_k^2 + c_x, x_0 = c_x\] \[y_ = 2 x_k y_k + c_y, y_0 = c_y\]
где \(k = 0, 1, 2, \dots, k_\max\) и \(\sqrt \leqslant r_\min\).
Составим матрицу M , элементы которой \(m_ \in [1; k_\max]\) равны номерам итераций, на которых процесс был остановлен. Далее матрицу можно вывести на экран как растровое изображение, предварительно сопоставив каждому числу из интервала \([1, k_\max]\) некоторый цвет.

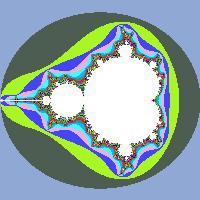
Если представить множество в общем виде:
то, изменяя значение N, можно получать симметричные фрактальные множества. Например, для \(N = 4\) и \(N = 7\):


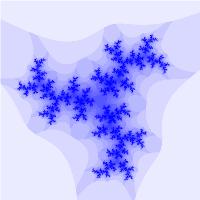
Фрактал Жюлиа
Рассмотрим ту же последовательность комплексных чисел, что и для множества Мандельброта:
\[z_ = z_k^2 + c, k = 0, 1, 2, \dots\]
Исходные данные, этапы построения и условия остановки – те же, что и для фрактала Мандельброта, за исключением:
- значение c фиксируется: \(c = 0,36 + 0,36i\)
- начальное значение \(z_0\) перебирается дискретно в области \(C \in [-1;1] + [-1;1]i\)

Рассматривая множество в общем виде: \(z_ = z_k^N + c\) и изменяя N и с, можно получать разнообразные фрактальные множества:
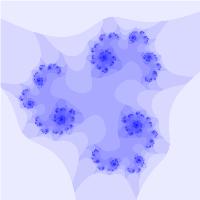

Бассейны Ньютона
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости.
Общая формула метода Ньютона имеет вид:
При выборе различных \(z_0\) процесс будет сходиться к различным корням (областям притяжения). Границы этих областей имеют фрактальную структуру.
Подставив \(p(z)\) в формулу метода, получим итерационную формулу для построения фрактала:
Итерационный процесс останавливается при:
\[\left| z_^3 \right| \leqslant r_\min\]
Для построения графической интерпретации также как и для фрактала Мандельброта, используется матрица, элементы которой равны номеру итерации, на которой остановился процесс.

Если записать формулу в общем виде:
\[p(z) = z^N - 1\] \[\left| z_^N - 1 \right| \leqslant r_\min\]
то можно получить изображения фракталов более сложной формы:



L-системы
В 1968 году венгерский биолог Аристид Линденмайер предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена для моделирования сложных ветвящихся структур (разнообразных растений). Эта модель получила название Lindenmayer System (Система Линденмайера или L-система).
Рекурсивная природа L-систем позволяет строить с их помощью геометрические фрактальные изображения.
L-система определяется как \(G = (V, \omega, P)\) , где
- V - алфавит – множество символов, содержащее элементы, которые могут быть замещены (переменные).
- ω – строка символов из множества V, определяющая начальное состояние системы (аксиома).
- P – набор правил, определяющий, как переменные могут быть замещены другими переменными и константами.
Правила применяются итеративно, начиная с аксиомы. За одну итерацию применяются одновременно все правила.
Например, L-система имеет вид:
Правила: \((A \rightarrow AB) (B \rightarrow BA)\)
После нескольких применений правил из аксиомы получаются строки:
Пример некоторых фракталов, построенных с помощью L-систем - кривая дракона и растение:


Лист папоротника
Существует несколько способов построения этого фрактала.
1) Построение с помощью системы итерируемых функций (IFS)
Производится 20 итераций функции \(f(x, y)\). Каждое новое значение получается из предыдущего в зависимости от случайного числа, т. е. вычисляется с использованием таблицы распределения:
| Вероятность | $$x'$$ | $$y'$$ |
|---|---|---|
| 0,01 | $$0$$ | $$0,16y$$ |
| 0,85 | $$0,85x + 0,04y$$ | $$-0,04x + 0,85y + 1,6$$ |
| 0,07 | $$0,20x - 0,26y$$ | $$0,23x + 0,22y + 1,6$$ |
| 0,07 | $$-0,15x + 0,28y$$ | $$0,26x + 0,24y + 0,44$$ |
После выполнения всех итераций точка рисуется на экране.
Начальные значения x и y могут быть константами (желательно не большими, чем 1) или их можно выбирать случайным образом на отрезке \([0;1]\).

2) Рекурсивное построение
Для построения используется процедура (псевдокод):
\(R(\phi) = \begin \cos(\phi) && \sin(\phi) \\ -\sin(\phi) && \cos(\phi) \end\) - матрица поворота на угол φ.
- \(p_0 = [x_0; y_0]\) - координаты начальной точки
- h – высота листа
- ψ – угол отклонения листа от вертикали
- side – направление изгиба ветви
- δ – минимальная длина ветви ветвящегося отрезка
- rec – максимальная глубина рекурсии
Рекомендуемые значения углов и коэффициентов: \(\phi_0 = 14,9^, \phi_1 = 37,7^, \phi_2 = 36,8^, \phi_3 = 17,6^, k_1 = 0,0483, k_2 = 0,162, m_1 = 0,371, m_2 = 0,336, m_3 = 0,849\).

Для получения более реалистичного изображения можно использовать метод управляемой случайности. Метод заключается в том, что в процесс сознательно вносятся помехи. В алгоритме построения ветви папоротника можно внести изменения в углы ветвления φ1, φ2, φ3.
Например, если ввести случайные воздействия на углы помех, равномерно распределенных на интервале \((-10^; 10^)\), можно получить изображения:


Литература:
Программы
Здесь приведены ссылки на программы, с помощью которых были созданы иллюстрации для этой статьи.
Построить повторно фрактал по исходному изображению практически невозможно. Открыв флэйм, вы получите исходный фрактал в точности.

Я уже рассказывала о простых способах создания фракталов, они подойдут даже начинающим. Еще один из таких способов – использование скрипта.
Эти фантастические цветы выполнены в программе Apophysis 7X16. Изображения получаются очень эффектными, а их создание не является сложным
Создайте потрясающие фрактальные цветы с помощью скрипта
Данный пост – это продолжение рассказа о том, как быстро создать фрактал. Сегодня я предлагаю добавить немного действий – два клика.

Для чего может понадобиться фрактал, который можно создать в один клик мышкой? Бывают ситуации, когда вам необходима уникальная картинка, допустим, чтобы ваш пост не смотрелся уныло. Но вы не художник и не владеете навыками компьютерной графики.

Фракталы, как известно, состоят из повторяющихся подобных элементов, поэтому в основе создания их в фотошопе лежат:
1. Создание основных элементов, которые будут повторяться, можно объединить их для удобства в один слой,
2. Копирование слоя с этими элементами с небольшим трансформированием (пропорциональным изменением масштаба и поворотом).
Рассмотрим пример создания одного из таких фракталов.
1. создайте новый документ с заданными размерами 1600 на 1200 пикселей, разрешение 72 пикс/дюйм, фон – белый.
2. Необязательным вспомогательным этапом является создание направляющих линий, проходящих через центр документа. Для их создания нужно отобразить линейки и протянуть эти линии от края документа к центру.

3. Выберите инструмент градиент с настройками:
![]()
цвета градиента выберите на свое усмотрение, часто фракталы создают на темном фоне, но это не обязательно. Я выбрала цвета:

теперь проведите направляющую линию по диагонали от нижнего правого угла в верхний левый для заливки градиентом.
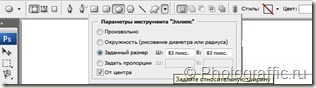
4. Выберите любую фигуру, которая будет в основе создания фрактала. Это может быть эллипс или любая другая несложная фигура. Выставьте следующие настройки для фигуры:
и нарисуйте фигуру в центре документа (на месте пересечения направляющих):

5. Проведите изменения в параметрах наложения слоя, для этого щелкните дважды мышкой по слою и в открывшемся окне примените стили тени, тиснения, контура, текстуры и наложения градиента:



Значение для контура оставьте по умолчанию, поставьте только галочку напротив этого пункта. Цвет градиент поставьте такой же, как и при создании фона. В результате преобразований получили такую фигуру:

6. Дублируйте слой 3 раза, нажав 3 раза сочетание клавиш Ctrl + J.
7. Выберите нижний слой с фигурой, и нажав Ctrl + T, увеличите ее в 2 раза:
![]()
и нажмите Enter.
8. При помощи инструмента перемещение распределите фигуры, получив, например, такую фигуру:
9. Для каждого слоя с фигурами примените команды Слой – Растрировать – Фигуру.
10. Нажмите на Shift и , не отпуская этой клавиши сделайте активными все слои с фигурами. Они выделятся синим.
11. Дублируйте слои, перетащив из на значок создания нового слоя.
12. Теперь выберите инструмент Перемещение и поставьте галочку в настройках этого инструмента (под горизонтальным меню) напротив пункта Показать направляющие элементы. Теперь Вы можете не только сдвигать одновременно выделенные слои, но и трансформировать их как вам угодно.
13. После видоизменения (перемещения и трансформирования слоев), еще раз дублируйте уже новые слои и измените уже новую группу:

И так повторяйте эти шаги до тех пор, пока не вырисуете определенную фигуру или рисунок.
Читайте также:


