Как сделать фрактал в экселе
Скучная офисная программа не только изменила работу финансистов, но и стала универсальной творческой средой.
Энтузиасты отмечают День Таблиц 17 октября — в этот день в 1979 году появилась VisiСalc, первая программа для таблиц. Она стала буквально революционной для финансистов и бухгалтеров и способствовала успеху Apple, потому что писалась именно под новый персональный компьютер Apple II.
Вокруг Excel и Google Таблиц выросла своя творческая культура — рисование, создание анимаций, игр и даже музыки. TJ рассказывает про одни из самых примечательных творений, созданных в ячейках.
Excel буквально создан для пиксель-арта — даже не имея навыков рисования можно легко собрать буквы или человека из закрашенных блоков-кирпичиков. Но художники пошли дальше и использовали инструменты контура, встроенных фигур, математических формул и VBA.
81-летний японец Тацуо Хориучи (Tatsuo Horiuchi) создаёт картины в Excel на протяжении двадцати лет. Всё началось перед выходом на пенсию в 2000 году — он решил не тратиться на холсты, кисти или софт, а освоил Excel-инструмент Autoshape. Хориучи не ожидал быстрых результатов, поэтому написал 10-летний план прогресса. Цель — нарисовать картину, которую не стыдно было бы показать людям.
Искусство привлекло внимание брендов — Microsoft пишет о картинах в своём блоге, а Google в 2016 году организовал коллаборацию двух иллюстраторов для создания картины в Google Таблицах. Результат перенесли на стену дома в Бруклине в качестве рекламной кампании.
Блог Марии Эсмеральдо " data-image-src="https://leonardo.osnova.io/b69291b2-b703-51ec-93ce-7a1b34cdbd04/">
Марина Эсмеральдо и Меллори Хейер на фоне их совместной картины, созданной в Google Таблицах Блог Марии Эсмеральдо
У известного художника Филипе Веласкеса (Felipe Velasquez) ушло 13 часов, чтобы нарисовать трансформера и три часа на Мастера Йоду. Те же картины можно получить через генераторы таблиц — уже минимум десять лет доступны утилиты, плагины и онлайн-сервисы, переводящие любое изображение в ячейки.
Одну из первых картин — что-то вроде кругов спирографом — Мэтью получил с помощью формулы Z=1.618^(abs(X)). Рисунки ниже потребовали более серьёзных вычислений:
Шелковников также провёл эксперимент по созданию одного и того же изображения в Excel и в Cinema 4D. Обе иллюстрации заняли около 12 часов, но в случае Cinema 4D ушло немного больше времени.
Трассировка лучей — это трёхмерная графика, изображающая свет на предметах. То, как лучи света падают, отражаются, преломляются и дают тень. Рассчитать все детали — трудная задача даже в специализированных программах. Но YouTube-блогер s0lly сделал это в Excel с анимацией шаров в 2019 году, а через два года превзошёл себя и улучшил первую версию. На gif-картинке внизу — вариант анимации 2021 года.
Основной способ создания анимаций и Excel-игр — макросы и язык программирования Visual Basic for Applications (VBA). Макрос — это встроенная функция Excel, которая по команде воспроизводит записанные пользователем действия. Например, выделяет все отрицательные суммы красным. VBA — язык, на котором пишутся макросы и более сложные алгоритмы внутри Excel.
Анимация шаров состоит из ряда формул, макрос отвечает за круговое движение. Версия на видео ускорена — в реальной жизни каждый кадр занимает около 2 секунд на процессинг даже на относительно мощном компьютере.
Отрывок из видео про анимацию американских горок в Excel. В начале показан объём расчётов, который позволяет осуществить движение YouTube-канал EngineeringFun
Музыкальный клип Joe Penna — не анимация, а набор кадров, каждый из которых он создавал вручную. На минутное видео ушло примерно 730 пиксельных автопортретов. Пожалуй, это самый весёлый видеоклип, созданный в таблицах.
YouTube-пользователь Alex C создал аналогичную стоп-моушен анимацию с реалистичной фигурой ребёнка, играющего в кубики. Но в его случае все движения программировались в VBA.
Игры в Excel — это целый отдельный жанр, в котором есть тысячи игр: от простого ячеечного тетриса и аркад до многоуровневых стратегий. Некоторые популярные игры обрели своих Excel-близнецов: Змейка, 2048, Скрэббл, Цивилизация, Minecraft, прототип легендарной Legend of Zelda под названием Excelda и другие.
Одна из самых известных игр на Excel появилась в 2013 году — Arena.Xlsm сделана в жанре RPG: больше 2000 видов врагов, 1131 магический предмет и 100 достижений. Её создал канадский бухгалтер Кэри Уолкин (Cary Walkin) во время учёбы на MBA. Практика с продвинутыми инструментами в Excel натолкнула его на мысль, что с этим можно создать полноценную игру. На финальную версию ушло пять месяцев.
Пользователь играет от лица бунтаря, чьё восстание против Императора провалилось и теперь он должен сражаться на арене против чудищ, чтобы выжить. Союзники извне присылают письма — сквозь них раскрываются другие персонажи, появляются инструкции и подсказки. У игры четыре концовки.
Все игровые кнопки находятся на экране: двигаться, атаковать, лечиться и применять заклинания. При повышении уровня можно прокачать силу атаки, защиты, точность и удачу. Чтобы сохранить прогресс, нужно буквально сохранить Excel-файл с игрой.
Стратегия не требует знания Excel — достаточно лишь скачать версию Excel 2007, 2010 или 2013 для Windows и включить макросы. Игра не совместима с Google Таблицами и MacOS.
По словам Уолкина, после выпуска Arena.Xlsm множество людей захотело выпускать собственные игры. Поэтому он выпустил курс с пошаговыми инструкциями по созданию игровых механик в Excel. А затем и инвестиционную Excel-игру Candy Number Crunch Saga с открытым исходным кодом, чтобы пользователи могли его исследовать и создавать свои собственные игры.
Основная активность вокруг Arena.Xlsm угасла около семи лет назад. Её создатель рассказал TJ, что сделал улучшенную версию игры для платформы Steam, но из-за проблемы с правами на дистрибуцию Excel игра так и не вышла.
В какой-то момент Кэри Уолкину пришлось выбрать приоритет: он работал в IT-компании, делал игры, консультировал других разработчиков и преподавал в университете по вечерам. Нагрузка была слишком высокая, и в итоге он покинул игровую индустрию и теперь работает в сфере SaaS.
Создание Excel-игр стало творческой отдушиной для парня, у которого не было настоящих творческих талантов. Если я помог другим людям раскрыть свои творческие способности, это было бы огромным достижением!
В рамках курса по созданию Excel-игр Уолкина другой разработчик Джордан Голдмайер (Jordan Goldmeier) написал 3D-лабиринт для Excel:
Делать сложные игры можно и без кода: в 2018 году блогер C Bel создал игровой 3D-движок, используя только формулы. Этот движок годится для шутеров от первого лица типа Doom и даёт похожий визуал: с поворотом вида, перемещением в пространстве, изменением освещения и столкновением со стенами.
Начальная версия игры с двумя уровнями заняла два года работы. Оставшиеся пять уровней вышли в 2019 году. Стало больше локаций, вариантов действий, игра усложнилась и сюжетно, и графически. В последствии шутер больше не обновляли, судя по блогу разработчика.
Dave vs Ziggy полностью написана на макросах Excel и включает стандартную палитру из 56 цветов. Музыку к игре тоже писал сам Шумаков.
В 2019 году Excel стал драм-машиной — YouTube-блогер Дилан Толлчиф (Dylan Tallchief) настроил таблицу таким образом, чтобы воспроизводить отмеченный ритм. Сама таблица не воспроизводит звук — она отсылает сигнал к встроенному программному синтезатору Microsoft GS Wavetable Synth. На Mac воспроизвести этот файл не получится. Но вместо этого плагина можно подключить другой девайс.
Проигрывание музыки через Excel — давно известная возможность программы. В 2015 году YouTube-блогер DJ Oamen показал, как создать и сыграть на мини-пианино в Excel, другие объясняли, как таблица проигрывает звук в зависимости от числового значения или как открыть медиаплеер внутри таблицы.
Несмотря на сотни арт-работ и игр, Excel как программа для искусства остаётся популярным только среди узкой группы людей, периодически вирусясь в интернете. Иногда это творчество выходит не только в офлайн-выставки: например, в Японии проводятся мастер-классы по рисованию Excel-картин в традиционном стиле. А 82-летняя программистка Масако Вакамия (Masako Wakamiya) нарисовала обложку для своей книги в Excel и печатает вееры и пакеты с узорами, созданными в таблицах. На встречу с императором Японии она пришла в одежде с Excel-принтами.
Статья создана участницей Лиги авторов. О том, как она работает и как туда вступить, рассказано в этом материале.

Многие из нас не подозревают о великолепии фрактального искусства или анимации в этом отношении. Вы можете использовать это искусство для украшения изображений и видео уникальными элементами. Фрактальное искусство состоит из математических вычислений фрактального объекта и отображения результата в виде анимации, неподвижных изображений и мультимедиа.
Генераторы фракталов, являющиеся неотъемлемой частью цифрового и компьютерного искусства, стремительно захватывают рынок. Вы можете использовать их и создавать захватывающие изображения, которые в противном случае было бы очень сложно создать, если бы генераторы фракталов не помогли вам.
Чтобы узнать больше об этом удивительном цифровом искусстве, давайте прочитаем статью! Мы составили для вас список фрактальных генераторов.
Часть 1: Лучший генератор фрактальной анимации
1. Mandelbulb 3D
Среди бесплатных генераторов фракталов популярным выбором является Mandelbulb 3D. Он может создавать трехмерные фрактальные изображения для формирования фрактальных объектов из множества нелинейных уравнений. Освещение, зеркальность, цвет, эффекты тени и свечения, а также глубина резкости включены в 3D-рендеринг, так что вы можете точно контролировать эффекты изображения. Он доступен для Windows и Mac Wineskin.
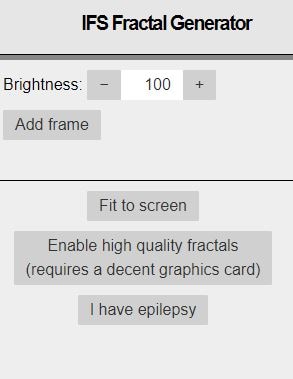
2. Fractal Generator
Если вам нужен генератор фрактальной анимации, этот инструмент вас не разочарует. У него простой для понимания интерфейс, где есть кнопки с именами "Создать", "Сохранить", "Экспорт изображения", "Анимировать", "Добавить кадр", "По размеру экрана", "Включить фракталы высокого качества" и "У меня эпилепсия". Кнопка "Новый" изменяет текущее фрактальное изображение или анимацию, тогда как "Сохранить" позволяет сохранить URL-адрес. Выбрав опцию "Экспортировать изображение", вы можете сохранить анимацию или фрактал изображения как файл PNG на своем компьютере. Вы можете добавить круглую рамку вокруг фрактального изображения или анимации, нажав опцию "Добавить рамку".
3. XenoDream
Этот генератор фракталов поддерживает 256 цветных изображений кнопок в теме Windows. В этой программе есть 12 шагов повтора/отмены для большей гибкости. Вы получаете параметры сетки для предварительного просмотра и имеете более 400 холонов с возможностью просмотра только выбранных холонов. Мощные редакторы текстур для фонового изображения, фильтр глубины резкости, постобработка стерео - вот лишь некоторые из элементов управления анимацией, которые вам понравятся. Вы даже можете импортировать, пробовать и упрощать градиенты. Доступны мягкие тени, экспорт облака точек, а также улучшения экспорта сетки.
4. FractalNow
Он предлагает инструменты для быстрого создания изображений с широким набором фракталов. Он использует инструмент командной строки FractalNow и графический инструмент QFractalNow. QFractalNow - это библиотека Qt, позволяющая исследовать фракталы для создания изображений. Усовершенствованные алгоритмы и эвристика помогают этим многопоточным инструментам быстро выполнять вычисления, и у них есть основные формулы, такие как Джулия, Мандельброт, Руди и так далее.
Часть 2: Лучший 2D-генератор фракталов
5. Ultra Fractal
Среди генераторов 2D-фракталов Ultra Fractal уникален тысячами типов фракталов и алгоритмов раскраски, 64-битной поддержкой со сверхбыстрым глубоким масштабированием, применением нескольких слоев для объединения нескольких фракталов в одно изображение и градиентами для добавления цвета. Вам не нужно разбираться в математике; этот инструмент может интуитивно помочь вам достичь желаемого результата.
6. Amazing Seattle Fractals
Это потрясающая коллекция фрактальных искусств, которая предоставляет вам больше информации о лучших фрактальных программах на рынке. Она состоит из их руководств, а также их высоких и низких точек, чтобы вы могли лучше их узнать.
7. Fractal Fr0st
Обсуждая бесплатные генераторы фракталов, нельзя игнорировать Fractal Fr0st. Благодаря великолепному графическому интерфейсу он предлагает вам много возможностей для фрактального искусства. Последние предложения в графическом интерфейсе включают - несколько уровней глубины в предварительном просмотре вариантов, которые четко объясняют действия каждой формы. Когда вы наводите указатель мыши на углы треугольника, они подсвечиваются. Системы с более чем двумя ядрами используют несколько потоков для отображения небольших превью.
8. FRAX
Этот бесплатный генератор фракталов имеет функции, с которыми никто не может сравниться. Начиная с CPU и GPU, он движется со скоростью в 400 раз выше, чем у аналогов. Будь то планшет или iPhone, Frax может невероятно преобразовать фрактальные изображения. 20 жестов multi-touch, организованные в 4 набора, позволяющие проводить пальцем, щипать, вращать, чтобы летать, и наклонять, чтобы управлять, предлагают лучшие результаты на рынке. Цветовые градиенты здесь плавно оттеняют и подкрашивают фрактал.
Часть 3: Генератор фракталов онлайн
9. UsefulJS
10. Science vs Magic
С помощью этого генератора фракталов вы можете видеть множество фрактальных изображений и анимаций. Однако вы не можете их сохранить, потому что это невозможно. Вы можете рандомизировать, сбросывать анимировать и менять цвет фона на черно-белый. Кроме того, здесь вы также можете увидеть тропу.
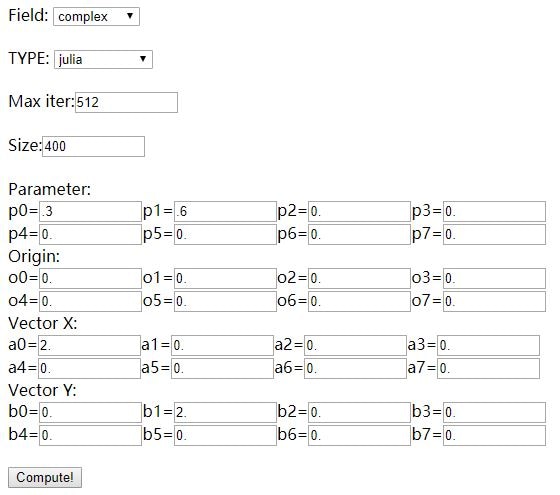
11. Online Fractal Generator
В этом онлайн-генераторе фракталов вам нужно установить поле, а также тип и нажать "Вычислить" для генерации результата. Вы можете увеличивать и уменьшать масштаб, вращать и изменять разрешение. Но мы не смогли найти ни одной опции для сохранения 2D-фрактального изображения.
Часть 4: Бесплатный генератор фракталов
12. ChaosPro
Если вы думаете, что вас встретит интересный интерфейс, извините, что разочаровал вас. Это простой интерфейс, в котором вы задумаетесь, с чего же начать. Это бесплатное программное обеспечение в реальном времени можно загрузить в вашу систему Windows, и оно поддерживает типы фракталов 3D и 2D. Также поддерживается анимация, истинные цвета. Вы можете писать свои собственные формулы и при этом получать быстрые результаты благодаря встроенному компилятору.
13. Apophysis
Это бесплатный генератор фракталов для компьютера под управлением Windows. Вы можете загрузить последнюю версию с веб-сайта в своей системе Windows, а затем выполнить желаемое фрактальное искусство в лучшем виде.
14. JWildfire
Это программное обеспечение доступно как для компьютеров Windows, так и для Mac. Системе Windows требуется дополнительный установщик Java, тогда как версия программного обеспечения для Mac представляет собой полный пакет без каких-либо дополнительных инструментов для его запуска. В нем есть множество блестящих фрактальных опций, с помощью которых вы можете создать свое изображение.
15. Fractal Landscapes
Здесь вы можете просматривать только фрактальные пейзажи или фрактальные ландшафты. Вы не можете изменить тип фрактального изображения или анимации. С точки зрения пользователя, пользоваться им сложно. Если вы хотите иметь более привлекательный и более интерактивный генератор фракталов, вы можете выбрать один из других генераторов из списка.
16. Fractal Map
Этот удивительный генератор фракталов доступен для систем Windows, Hub и HoloLens. Вы можете создавать фрактальные изображения в реальном времени с параллельной обработкой. Он поддерживает 8 процессоров или ядер для быстрого рендеринга и дает вам целый мир циклических анимаций. Теперь вы можете удалять анимацию, использовать циклическое переключение цветов, а также использовать его на испанском языке. Вы можете получить это программное обеспечение в официальном магазине Microsoft.
У меня нет опыта программирования фракталов. Конечно, я видел знаменитые изображения Мандельброта и т.д.
Можете ли вы предоставить мне простые алгоритмы для фракталов.
Я знаю, что если я google фракталы, я получаю много (сложной) информации, но я хотел бы начать с простого алгоритма и играть с ним.
Предложения по улучшению основного алгоритма также приветствуются, например, как сделать их в этих прекрасных цветах и т.д.
ОТВЕТЫ
Ответ 1
Программирование Мандельброта очень просто.
Мой код quick-n-dirty ниже (не обязательно без ошибок, но с хорошей схемой).
Вот набросок: Множество Мандельброта лежит в комплексной сетке полностью внутри круга с радиусом 2.
Итак, начните с сканирования каждой точки в этой прямоangularьной области. Каждая точка представляет комплексное число (x + yi). Выполните итерацию этого комплексного числа:
[new value] = [old-value]^2 + [original-value] , отслеживая две вещи:
1.) количество итераций
2.) расстояние [нового значения] от источника.
Если вы достигли максимального числа итераций, все готово. Если расстояние от начала координат больше 2, все готово.
Когда закончите, раскрасьте оригинальный пиксель в зависимости от количества итераций, которые вы сделали. Затем перейдите к следующему пикселю.
Некоторые детали опущены:
1.) Узнайте, что такое квадрат комплексного числа и как его рассчитать.
2.) Узнайте, как преобразовать прямоangularьную область (-2, 2) в координаты экрана.
Ответ 2
Вы действительно должны начать с набора Мандельброта и понять, что это на самом деле.
Идея этого относительно проста. Вы начинаете с функции комплексной переменной
где z - комплексная переменная, а C - комплексная постоянная. Теперь вы повторяете его, начиная с z = 0, то есть вычисляете z 1= f (0), z 2= f (z 1), z 3= f (z 2) и так далее. Множество тех констант C, для которых последовательность z 1, z 2, z 3 . ограничена, т.е. Не стремится к бесконечности, является множеством Мандельброта (черный цвет на рисунке на странице Википедии).
На практике, чтобы нарисовать набор Мандельброта, вы должны:
- Выберите прямоугольник в комплексной плоскости (скажем, от точки -2-2i до точки 2 + 2i).
- Покройте прямоугольник подходящей прямоугольной сеткой точек (скажем, 400x400 точек), которая будет отображаться в пикселях на вашем мониторе.
- Для каждой точки/пикселя пусть C будет этой точкой, вычислите, скажем, 20 членов соответствующей итерированной последовательности z 1, z 2, z 3 . и проверьте, "уходит ли она в бесконечность". На практике во время итерации вы можете проверить, больше ли абсолютное значение одного из 20 слагаемых, чем 2 (если одно из слагаемых имеет значение, последующие слагаемые гарантированно будут неограниченными). Если некоторый z_k делает, последовательность "уходит в бесконечность"; в противном случае вы можете считать его ограниченным.
- Если последовательность, соответствующая определенной точке C, ограничена, нарисуйте соответствующий пиксель на рисунке черным цветом (поскольку он принадлежит набору Мандельброта). В противном случае нарисуйте его другим цветом. Если вы хотите повеселиться и создать красивые сюжеты, нарисуйте их разными цветами в зависимости от величины абс (20-й член).
Поразительный факт о фракталах состоит в том, как мы можем получить чрезвычайно сложный набор (в частности, границу набора Мандельброта) из простых и, очевидно, безобидных требований.
Ответ 3
Если комплексные числа дают вам головную боль, существует широкий диапазон фракталов, которые можно сформулировать с использованием L-системы. Для этого требуется взаимодействие нескольких слоев, но каждый из них интересен в своем собственном праве.
Затем вам понадобится слой для выполнения L-системы. L-системы связаны с Post-systems и Системы Semi-Thue, и, как и virii, они оседлали границу Тьюринга. Концепция переписывается по строкам. Он может быть реализован как макрорасширение или процедура с дополнительными элементами управления для привязки рекурсии. Если вы используете макрорасширение (как в примере ниже), вам все равно потребуется процедура, предназначенная для сопоставления символов командам черепахи и процедуры для итерации по строке или массиву для запуска программы кодированных черепах. Для набора процедур ограниченной рекурсии (например,) вы вставляете команды черепахи в процедуры и либо добавляете проверки уровня рекурсии к каждой процедуре, либо учитываете ее обработчика.
Вот пример дерева Пифагора в постскриптуме с использованием макроразложения и очень сокращенного набора команд черепахи. Для некоторых примеров в python и mathematica см. Мой вызов кода для гольфа.

Ответ 4
Один из примеров - простая реализация Мандельброта.
Ответ 5
Еще один отличный фрактал для изучения - фрактальный треугольник Серпинского.
В принципе, нарисуйте три угла треугольника (желательно односторонний, но любой треугольник будет работать), затем запустите точку P в одном из этих углов. Переместите P на полпути к любому из трех углов в случайном порядке и нарисуйте там точку. Снова переместите P на полпути к произвольному углу, нарисуйте и повторите.
Вы думаете, что случайное движение создаст случайный результат, но на самом деле это не так.
Ответ 6
Треугольник Серпинского и кривая Коха представляют собой специальные типы фракталов пламени. Фракталы пламени - это очень обобщенный тип итерированной функциональной системы, поскольку он использует нелинейные функции.
Алгоритм IFS: es выглядит следующим образом:
Start with a random point.
Повторите следующие много раз (по крайней мере, миллион, в зависимости от размера конечного изображения):
Apply one of N predefined transformations (matrix transformations or similar) to the point. An example would be that multiply each coordinate with 0.5. Plot the new point on the screen.
Если точка находится за пределами экрана, вместо этого произвольно выберите новую, расположенную внутри экрана.
Если вам нужны красивые цвета, пусть цвет зависит от последнего использованного преобразования.
Ответ 7
Я бы начал с чего-то простого, например Koch Snowflake. Это простой процесс взятия строки и ее преобразования, а затем повторение процесса рекурсивно, пока он не выглядит аккуратным.
Что-то супер простое, как взять 2 очка (строка) и добавить третью точку (сделать угол), а затем повторить на каждом новом созданном разделе.
Ответ 8
Ответ 9
Я думаю, вы не видите фракталов как алгоритм или что-то программировать. Фракталы - это концепция! Это математическая концепция повторяющегося шаблона.
Поэтому вы можете создать фрактал разными способами, используя разные подходы, как показано на рисунке ниже.

Выберите подход, а затем исследуйте, как его реализовать. Эти четыре примера были реализованы с использованием Marvin Framework. Исходные коды доступны здесь
Ответ 10
Набор mandelbrot генерируется путем многократной оценки функции до ее переполнения (некоторый определенный предел), а затем проверки того, сколько времени потребовалось для переполнения.
Значение представляет собой комплексное число. комплексное число (a + bi) квадратично, чтобы дать (aa-b * b + 2 * abi). Вам придется использовать сложный тип или включать этот расчет в ваш цикл.
Ответ 11
Здесь простой и понятный код в Java для mandelbrot и других фрактальных примеров
Просто загрузите BuildFractal.jar, чтобы протестировать его на Java и выполните команду:
java -Xmx1500M -jar BuildFractal.jar 1000 1000 по умолчанию MANDELBROT
Исходный код также доступен для загрузки/изучения/редактирования/расширения.
Ответ 12
Ну, простые и графически привлекательные не идут рука об руку. Если вы серьезно относитесь к программированию фракталов, я предлагаю прочитать на итерированных функциональных системах и достижения, которые были сделаны в их рендеринге.
Ответ 13
Люди, находящиеся выше, используют поиск средних точек для sierpinski и Koch, я бы более рекомендовал копировать фигуры, масштабировать их, а затем переводить их для достижения "фрактального" эффекта. Псевдокод в Java для sierpinski будет выглядеть примерно так:
Ответ 14
Иногда я программирую фракталы для удовольствия и как вызов. Здесь вы можете найти здесь. Код написан в Javascript, используя библиотеку P5.js и может быть прочитан непосредственно из исходного кода HTML.
Для тех, кого я видел, алгоритмы довольно просты, просто найдите основной элемент, а затем повторите его снова и снова. Я делаю это с помощью рекурсивных функций, но это можно сделать по-другому.
Книга Сергея Деменока [1] мне понравилась, кое-что прояснила в моем понимании фракталов. Возможно, она лучше подойдет для первого знакомства с темой, чем труды первооткрывателя фракталов Бенуа Мандельброта.

Купить бумажную книгу в Ozon
Часть I. ПУТЕШЕСТВИЕ К ИСТОКАМ
МИФЫ И МИСТИФИКАЦИИ. Открытый Мандельбротом новый пласт форм стал золотой жилой для дизайнеров, архитекторов, инженеров. Несчётное число фракталов строится по одним и тем же принципам многократного повторения. Отсюда фрактал проще всего определить, как геометрическую форму, которая содержит в себе повторяющиеся элементы в любом масштабе. Эта геометрическая форма локально неизменна (инвариантна), масштабно самоподобна и целостна в своей ограниченности истинная сингулярность, сложность которой раскрывается по мере приближения, а на удалении сама тривиальность.
ДЬЯВОЛЬСКАЯ ЛЕСТНИЦА. Для передачи данных между компьютерами используются чрезвычайно сильные электрические сигналы. Такой сигнал дискретен. Помехи или шумы случайно возникают в электрических сетях вследствие многих причин и приводят к потере данных при передаче информации между компьютерами. Исключить влияние шумов на передачу данных в начале шестидесятых годов прошлого века было поручено группе инженеров IBM, в работе которой принимал участие Мандельброт.
Грубый анализ показал наличие периодов, во время которых не регистрировалось ни одной ошибки. Выделив периоды длительностью в час, инженеры заметили, что между ними периоды прохождения сигнала без ошибок также прерывисты здесь возникают более короткие паузы длительностью около двадцати минут. Таким образом, передача данных без ошибок характеризуется пакетами данных разной длины и паузами в шумах, в течение которых сигнал передаётся без ошибок. В пакетах более высокого ранга как бы встроены пакеты более низкого. Подобное описание предполагает существование такого понятия, как относительное расположение пакетов низшего ранга в пакете более высокого ранга. Опыт показал, что распределение вероятностей этих относительных расположении пакетов не зависит от их ранга. Такая инвариантность говорит о самоподобии процесса искажения данных под действием электрических шумов. Сама процедура вырезания свободных от ошибок пауз в сигнале при передаче данных не могла прийти в голову инженерам-электрикам по той причине, что для них такое было внове.
Часть II. ФРАКТАЛЫ СУТЬ ДЕЛА
В этой простой формуле Ричардсона L есть измеренная длина побережья, ε – величина шага измерения, а β ≈ 3/2 – найденная им степень роста длины побережья с уменьшением шага измерения. В отличие от длины окружности, длина береговой линии Великобритании возрастает, не имея 55 предела. Она бесконечна! Приходиться смириться с тем, что кривые изломанные, негладкие не имеют предельной длины.
Однако исследования Ричардсона наводили на мысль, что они имеют некоторую характерную меру степень роста длины с уменьшением масштаба измерения. Оказалось, что именно эта величина мистическим образом идентифицирует ломаную линию как отпечаток пальцев личность человека. Мандельброт интерпретировал береговую линию как фрактальный объект – объект, размерность которого совпадает с показателем степени β.
Например, размерности прибрежных пограничных кривых для западного побережья Норвегии – 1,52; для Великобритании – 1,25; для Германии – 1,15; для Австралии – 1,13; для сравнительно гладкого побережья Южной Африки – 1,02 и, наконец, для идеально гладкой окружности – 1,0.
Рекурсию можно проиллюстрировать рядом Фибоначчи, представленным в форме последовательности Жирара:
Результат – числа Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
В этом примере совершенно очевидно, что функция применяется сама к себе, не отсылая к начальному значению. Она как бы скользит по ряду Фибоначчи, и каждый результат предыдущей итерации становится начальным значением для следующей. Именно такое повторение реализуется при построении фрактальных форм.
Метод вырезания. Берём равносторонний треугольник со стороной r. На первом шаге вырезаем в центре него перевёрнутый вершиной вниз равносторонний треугольник с длиной стороны r1 = r0/2. В результате этого шага у нас получаются три равносторонних треугольника с длинами сторон r1 = r0/2, располагающиеся в вершинах исходного треугольника (рис. 2).
Метод SIF, или Метод систем итерированных функций Барнсли. Дано: равносторонний треугольник с координатами углов А (0,0), В (1,0), С (1/2, √3/2). Z0 – произвольная точка внутри этого треугольника (рис. 3). Берем игральную кость, на гранях которой имеется по две буквы А, В и С.
Шаг 1. Бросаем кость. Вероятность выпадения каждой буквы составляет 2/6 = 1/3.
- Если выпала буква А строим отрезок z0–A, на середине которого ставим точку z1
- Если выпала буква В строим отрезок z0–B, на середине которого ставим точку z1
- Если выпала буква С строим отрезок z0–C, на середине которого ставим точку z1
Шаг 2. Бросаем кость ещё раз.
- Если выпала буква А строим отрезок z1–A, на середине которого ставим точку z2
- Если выпала буква В строим отрезок z1–B, на середине которого ставим точку z2
- Если выпала буква С строим отрезок z1–C, на середине которого ставим точку z2
ПЕТЛЯ ОБРАТНОЙ СВЯЗИ. Основоположник кибернетики Норберт Винер для описания петли обратной связи в качестве примера привёл рулевого на лодке. Рулевой должен придерживаться заданного курса и постоянно проводит оценку того, насколько лодка его придерживается. Если рулевой видит, что лодка отклоняется, он поворотом руля возвращает её на заданный курс. Через некоторое время он снова производит оценку и опять корректирует направление движения при помощи руля. Таким образом, навигация осуществляется при помощи итераций, повтора и последовательного приближения движения лодки к заданному курсу.
Типовая схема петли обратной связи показана на рис. 4 Она сводится к изменению переменного параметрах (направление лодки) и контролируемого параметра С (курс лодки).
Рис. 4 Схема петли обратной связи
Теперь один шаг эволюции во времени состоит в том, что последовательность нулей и единиц сдвигается влево на одну позицию, и цифра, оказавшаяся по левую сторону от запятой, отбрасывается:
Заметим, что если исходные числа х0 рациональные, то в процессе итерации значения хn выходят на периодическую орбиту. Например, для начального числа 11/24 в процессе итерации получим ряд значений:
11/24 -> 11/12 -> 5/6 -> 2/3 -> 1/3 -> 2/3 -> 1/3 -> …
Если исходные значения x0 иррациональны, отображение никогда не выйдет на периодический режим. В интервале исходных значений x0 ∈ [0,1] содержится бесконечно много точек рациональных и бесконечно много точек иррациональных. Таким образом, плотность периодических орбит равна плотности орбит, которые никогда не выходят на периодический режим. В любой окрестности рационального значения x0 найдётся иррациональное значение исходного параметра х’0 При таком положении дел неизбежно возникает тонкая чувствительность к начальным условиям. Это является характерным признаком того, что система находиться в состоянии динамического хаоса.

Рис. 5. Мауриц Эшер. Рисующие руки. 1948

Рис. 6. Виды аттракторов
К 1971 году в научной литературе уже имелся один набросок такого аттрактора. Эдуард Лоренц сделал его приложением к своей статье о детерминистском хаосе, вышедшей в 1963 году. Этот аттрактор был устойчивым, непериодическим, имел малое число степеней свободы и никогда не пересекал сам себя. Если бы подобное случилось, и он возвратился в точку, которую уже миновал, движение в дальнейшем повторялось бы, образуя тороидальный аттрактор, но такого не происходило.
Странность аттрактора заключается, как считал Рюэль, в трёх неэквивалентных, но на практике существующих вместе признаках:
- фракталъности (вложенность, подобие, согласованность);
- детерминированности (зависимость от начальных условий);
- сингулярности (конечное число определяющих параметров).
Часть III. МНИМАЯ ЛЁГКОСТЬ ФРАКТАЛЬНЫХ ФОРМ
![]()
В XIX веке трудами Эйлера, Аргана, Коши, Гамильтона разрабатывается арифметический аппарат работы с комплексными числами. Любое комплексное число может быть представлено как сумма X+iY, где X и Y – привычные нам вещественные числа, а i мнимая единица (по сути это √–1). Каждому комплексному числу соответствует точка с координатами на так называемой комплексной плоскости.
Второе важное понятие – фазовый портрет динамической системы сформировалось в XX веке. После того, как Эйнштейн показал, что по отношению к свету всё движется с одинаковой скоростью, идея о возможности выразить динамическое поведение системы в формате застывших геометрических линий так называемом фазовом портрете динамической системы обрела ясный физический смысл.
Проиллюстрируем её на примере маятника. Первые опыты с маятником Жан Фуко проводил в 1851 году в погребе, потом в Парижской обсерватории, потом под куполом Пантеона. Наконец, в 1855 году маятник Фуко был подвешен под куполом парижской церкви Сен-Мартен-де-Шан. Длина каната маятника Фуко 67 м, вес гири 28 кг. С огромного расстояния маятник выглядит как точка. Точка всегда неподвижна. Приближаясь, мы различим систему с тремя типовыми траекториями: гармонический осциллятор (sinϕ ≈ ϕ), маятник (колебания взад-вперёд), пропеллер (вращение).
Рис. 8. Маятник: а) траектория в фазовом пространстве идеального маятника; б) траектория в фазовом пространстве маятника, качающегося с затуханием; в) фазовый портрет
В фазовом пространстве может не быть длин, длительностей, движений. Здесь любое действие пред-дано, но не всякое действительно. От геометрии остаётся только топология, вместо мер параметры, вместо размеров размерности. Здесь любая динамическая система имеет свой уникальный отпечаток фазовый портрет. И среди них встречаются фазовые портреты довольно странные: будучи сложными, они определены одним-единственным параметром; будучи соизмеримыми, они несоразмерны; будучи непрерывными, они дискретны. Такие странные фазовые портреты характерны для систем с фрактальной конфигурацией аттракторов. Дискретность центров притяжения (аттракторов) создаёт эффект кванта действия, эффект разрыва или скачка при том, что траектории сохраняют непрерывность и производят единую связанную форму странный аттрактор.
КЛАССИФИКАЦИЯ ФРАКТАЛОВ. Фрактал имеет три ипостаси: формальную, операциональную и символическую, которые ортогональны друг другу. И это значит, что одна и та же форма фрактала может быть получена посредством разных алгоритмов, а одно и то же число фрактальная размерность может появиться у совершенно разных по форме фракталов. С учетом этих замечаний классифицируем фракталы по символическому, формальному и операциональному признакам:
- в символическом плане характерная для фрактала размерность может быть целой или дробной;
- по формальному признаку фракталы могут быть связные, как лист или облако, и несвязные, как пыль;
- по операциональному признаку фракталы могут быть разделены на регулярные и стохастические.
Регулярные фракталы строятся по строго определённому алгоритму. Процесс построения при этом обратим. Вы можете повторить все операции в обратном порядке, стирая любой созданный в процессе детерминированного алгоритма образ, точка за точкой. Детерминированный алгоритм может быть линейным или нелинейным.
ЛИНЕЙНЫЕ ФРАКТАЛЫ. Линейные фракталы названы так по той причине, что все они строятся по определённому линейному алгоритму. Эти фракталы самоподобны, не искажаются при любом изменении масштаба и не дифференцируемы в любой своей точке. Для построения таких фракталов достаточно задать основу и фрагмент. Эти элементы будут многократно повторяться с уменьшением масштаба до бесконечности.
Пыль Кантора. В XIX веке немецкий математик Георг Фердинанд Людвиг Филипп Кантор (1845–1918) предложил математическому сообществу странное множество чисел в интервале от 0 до 1. Множество содержало бесконечное число элементов в указанном промежутке и притом имело нулевую размерность. Пущенная наугад стрела вряд ли поразила бы хоть один элемент этого множества.

Рис. 9. Ковёр Серпинского

Рис. 10. Построение кривой Пеано
При том, что топологическая размерность кривой Пеано равна единице, её фрактальная размерность равна d = ln(1/9)/ln(1/3) = 2. В рамках фрактальной геометрии парадокс разрешился самым естественным образом. Линией, как паутиной, можно покрыть плоскость. При этом устанавливается однозначное соответствие: каждой точке линии соответствует точка на плоскости. Но это соответствие не взаимно-однозначное, ведь каждой точке на плоскости соответствует одна или более точек на линии.

Рис. 11. Построение фрактала Гильберта
Кривая Гильберта стала первым примером FASS-кривых (spaceFilling, selfAvoiding, Simple and selfSimilar заполняющих пространство само избегающих, простых и самоподобных линий). Фрактальная размерность линии Гилберта, как и кривой Пеано, равна двум.

Рис. 12. Построение фрактала Германа Минковского
НЕЛИНЕЙНЫЕ ФРАКТАЛЫ. Простейшим нелинейным отображением комплексной плоскости на себя является рассмотренное в первой части отображение Жюлиа z g z 2 + С. Оно представляет собой расчёт по замкнутому циклу, в котором результат предыдущего цикла умножается сам на себя с приплюсовыванием к нему некоей константы, т. е. представляет собой квадратичную петлю обратной связи (рис. 13).

Рис. 13. Квадратичная петля обратной связи
В процессе итераций при фиксированной величине константы С, в зависимости от произвольной начальной точки Z0, точка Zn при n -> ∞ может быть или конечной, или бесконечной. Всё зависит от положения Z0 относительно начала отсчёта z = 0. Если расчётная величина конечна, то она включается в множество Жюлиа; если уходит на бесконечность, то отсекается от множества Жюлиа.
Разнообразие форм Жюлиа обескуражило математиков, когда они впервые смогли наблюдать эти формы на мониторах компьютеров. Попытки ранжировать это многообразие носили весьма условный характер и свелись к тому, что за основу классификации отображений Жюлиа было взято множество Мандельброта, границы которого, как оказалось, асимптотически подобны отображениям Жюлиа.
При С = 0 повторение отображения Жюлиа даёт последовательность чисел z0, z0 2 , z0 4 , z0 8 , z0 16 … В итоге возможны три варианта:
- при |z0| 1 в ходе итераций числа zn по модулю увеличиваются, стремясь к бесконечности. В этом случае аттрактором является бесконечно удалённая точка, и такие значения мы исключаем из множества Жюлиа;
- при |z0| = 1 все точки последовательности продолжают оставаться на этой единичной окружности. В этом случае аттрактором является окружность.
Таким образом, при С = 0 граница между притягивающими и отталкивающими исходными точками есть круг. В этом случае отображение имеет две неподвижные точки: z = 0 и z = 1. Первая из них является притягивающей, так как производная квадратичной функции в нуле есть 0, а вторая отталкивающей, так как производная квадратичной функции при значении параметра единица равна двум.
Рассмотрим ситуацию, когда постоянная С является действительным числом, т.е. мы как бы перемещаемся по оси множества Мандельброта (рис. 14). При С = –0,75 происходит самопересечение границы множества Жюлиа и появляется второй аттрактор. Фрактал в этой точке носит имя фрактала Сан-Марко, данное ему Мандельбротом в честь известного венецианского собора. Глядя на рисунок, нетрудно понять, почему Мандельброту пришла идея назвать фрактал именно в честь этого строения: сходство потрясающее.
Рис. 14. Изменение формы множества Жюлиа при уменьшении действительной величины С от 0 до –1
Уменьшая далее С до –1,25, мы получим новую типовую форму с четырьмя неподвижными точками, которые сохраняются до значений С Валерий 19.04.2016 в 21:45
Войти
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Программы генераторы фракталов
Основные генераторы фракталов




Читайте также: