Как расшифровать rsa файл
Криптосистема [math]\mathtt[/math] стала первой системой, пригодной и для шифрования, и для цифровой подписи.
Содержание
Алгоритм [math]\mathtt[/math] включает в себя четыре этапа: генерация ключей, передача ключей, шифрование и расшифрование.
Криптографические системы с открытым ключом используют так называемые односторонние функции.
Под односторонностью понимается не теоретическая однонаправленность, а практическая невозможность вычислить обратное значение, используя современные вычислительные средства, за обозримый интервал времени.
[math]\mathtt[/math] -ключи генерируются следующим образом:
- Выбираются два различных случайных простых числа [math]p[/math] и [math]q[/math] заданного размера (например, [math]1024[/math] бита каждое).
- Вычисляется их произведение [math]n=p\cdot q[/math] , которое называется модулем.
- Вычисляется значение функции Эйлера от числа [math]n[/math] : [math]\varphi(n) = (p-1)\cdot (q-1).[/math]
- Выбирается целое число [math]e[/math] ( [math]1 \lt e \lt \varphi(n)[/math] ), взаимно простое со значением функции [math]\varphi(n)[/math] . Обычно в качестве [math]e[/math] берут простые числа, содержащие небольшое количество единичных бит в двоичной записи.
- Число [math]e[/math] называется открытой экспонентой (англ. public exponent)
- Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в [math]e[/math] .
- Слишком малые значения [math]e[/math] , например [math]3[/math] , потенциально могут ослабить безопасность схемы [math]\mathtt[/math] .
- Вычисляется число [math]d[/math] , мультипликативно обратное к числу [math]e[/math] по модулю [math]\varphi(n)[/math] , то есть число, удовлетворяющее сравнению: [math]d\cdot e \equiv 1 \pmod.[/math] Примечание Сравнеие двух целых чисел по модулю натурального числа [math]m[/math] — математическая операция, позволяющая ответить на вопрос о том, дают ли два выбранных целых числа при делении на [math]m[/math] один и тот же остаток. Любое целое число при делении на [math]m[/math] дает один из [math]m[/math] m возможных остатков: число от [math]0[/math] до [math]m-1[/math] .
- Число [math]d[/math] называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
- Пара [math]\left\< e, n \right\>[/math] публикуется в качестве открытого ключа [math]\mathtt[/math] (англ. [math]\mathtt[/math] public key).
- Пара [math]\left\< d, n \right\>[/math] играет роль закрытого ключа [math]\mathtt[/math] (англ. [math]\mathtt[/math] private key) и держится в секрете.

Действительно, для [math]\forall m \in \mathbb_[/math]
[math]\forall m \in \mathbb_: m^ \equiv m \pmod
[/math] .
Возможны два случая:
- [math]m \not\equiv 0 \pmod
[/math] .
Поскольку числа [math]e[/math] и [math]d[/math] являются взаимно обратными относительно умножения по модулю [math]\varphi(n)=(p-1)(q-1)[/math] , то есть
[math]ed=1+k(p-1)(q-1)[/math] для некоторого целого [math]k[/math] ,
[math]\begin m^ & \equiv m^ \right)\left( \right)> \pmod
\\ & \equiv m\left( > \right)^ \\ & \equiv m\left( 1 \right)^ \equiv m \pmod \end[/math] где второе тождество следует из теоремы Ферма. [math]m^ \equiv 0 \pmod \equiv m \pmod [/math] Таким образом, при всех [math]m[/math] выполняется равенство [math]m^ \equiv m \pmod [/math] Аналогично можно показать, что: [math]\forall m \in \mathbb_: m^ \equiv m \pmod[/math] . Стойкость алгоритма основывается на сложности вычисления обратной функции к функции шифрования [math]c = E(m) = m ^ e \mod n[/math] . Для вычисления [math]m[/math] по известным [math]c, e, n[/math] нужно найти такой [math]d[/math] , чтобы [math]e \cdot d \equiv 1 \pmod,[/math] Вычисление обратного элемента по модулю не является сложной задачей, однако злоумышленнику неизвестно значение [math]\varphi(n)[/math] . Для вычисления функции Эйлера от известного числа [math]n[/math] необходимо знать разложение этого числа на простые множители. Нахождение таких множителей и является сложной задачей, а знание этих множителей — «потайной дверцей» (англ. backdoor), которая используется для вычисления [math]d[/math] владельцем ключа. Существует множество алгоритмов для нахождения простых сомножителей, факторизации, самый быстрый из которых на сегодняшний день — общий метод решета числового поля, скорость которого для k-битного целого числа составляет [math] \exp (( c + o(1))k^> \log^>k)[/math] для некоторого [math]c \lt 2[/math] . В [math]2010[/math] году группе учёных из Швейцарии, Японии, Франции, Нидерландов, Германии и США удалось успешно вычислить данные, зашифрованные при помощи криптографического ключа стандарта [math]\mathtt[/math] длиной [math]768[/math] бит. Нахождение простых сомножителей осуществлялось общим методом решета числового поля. По словам исследователей, после их работы в качестве надежной системы шифрования можно рассматривать только [math]\mathtt[/math] -ключи длиной [math]1024[/math] бита и более. Причём от шифрования ключом длиной в [math]1024[/math] бит стоит отказаться в ближайшие три-четыре года. С [math]31[/math] декабря [math]2013[/math] года браузеры Mozilla перестали поддерживать сертификаты удостоверяющих центров с ключами [math]\mathtt[/math] меньше [math]2048[/math] бит. Алгоритм шифрования сеансового ключа выглядит следующим образом: При неправильной или неоптимальной реализации или использовании алгоритма возможны специальные криптографические атаки, такие как атаки на схемы с малой секретной экспонентой или на схемы с общим выбранным значением модуля. Вокруг алгоритмов шифрования с отрытым и закрытым ключом существует множество недопониманий и мистификаций. Здесь я хотел бы предельно коротко и наглядно, с конкретными числами и минимумом формул, показать, как это работает. Я не вдаюсь в теорию (не очень понятно, на какой уровень подготовки читателя следует рассчитывать), но я уверен, что прочитав эту короткую иллюстрацию, любому человеку будет проще разобраться в формулах и строгих доказательствах. Итак. Допустим, я хочу получить от вас некие данные. Мы с вам не хотим, чтобы эти данные узнал кто-то, кроме нас. И у нас нет никакой уверенности в надёжности канала передачи данных. Приступим. Я должен проделать предварительные действия: сгенерировать публичный и приватный ключ. Мне нужно вычислить число d , обратное е по модулю φ . То есть остаток от деления по модулю φ произведения d×e должен быть равен 1. Запишем это в обозначениях, принятых во многих языках программирования: (d×е)%φ=1 . Или (d×5)%12=1 . d может быть равно 5 ( (5×5)%12=25%12=1 ), но чтобы оно не путалось с e в дальнейшем повествовании, давайте возьмём его равным 17. Можете проверить сами, что (17×5)%12 действительно равно 1 ( 17×5-12×7=1 ). Итак d=17 . Пара — это секретный ключ, его я оставляю у себя. Его нельзя сообщать никому. Только обладатель секретного ключа может расшифровать то, что было зашифровано открытым ключом. Строго говоря, вам вовсе незачем вычислять огромное число «19 в степени 5». При каждом умножении достаточно вычислять не полное произведение, а только остаток от деления на 21. Но это уже детали реализации вычислений, давайте не будем в них углубляться. Полученные данные E=10 , вы отправляете мне. Я получил ваши данные ( E=10 ), и у меня имеется закрытый ключ = . Надёжность шифрования обеспечивается тем, что третьему лицу (старающемуся взломать шифр) очень трудно вычислить закрытый ключ по открытому. Оба ключа вычисляются из одной пары простых чисел ( p и q ). То есть ключи связаны между собой. Но установить эту связь очень сложно. Основной загвоздкой является декомпозиция модуля n на простые сомножители p и q . Если число является произведением двух очень больших простых чисел, то его очень трудно разложить на множители. Постараюсь это показать на примере. Давайте разложим на множители число 360: Мы на каждом шагу, практически без перебора, получали всё новые и новые множители, легко получив полное разложение 360=2×2×2×3×3×5 Давайте теперь возьмём число 361. Тут нам придётся помучиться. При использовании больших чисел, задача становится очень сложной. Это позволяет надеяться, что у взломщика просто не хватит вычислительных ресурсов, чтобы сломать ваши шифр за обозримое время. Оттолкнёмся от пары простых чисел = . Пусть наш открытый ключ будет = , а закрытый = . Мы готовы к шифрованию. Переведём наше слово в цифровое представление. Мы можем взять просто номера букв в алфавите. У нас получится последовательность чисел: 11, 17, 15, 19. Мы можем зашифровать каждое из этих чисел открытым ключом = и получить шифровку 197, 272, 2, 304. Эти числа можно передать получателю, обладающему закрытым ключом = и он всё расшифрует. Последовательность (11, 28, 43, 62) получается «запутанной». Все буквы в ней как бы перемешаны, в том смысле, что на каждый код влияет не одна буква, а все предыдущие. То есть мы можем добавить случайное число в начало и получить (299, 11, 17, 15, 19). После перемешивания получится: 299, 310, 4, 19, 38. После шифрования уже невозможно будет догадаться где была какая буква. Детали и принципы формирования блоков можно почитать тут. Я же в этой заметке хотел рассказать только про RSA. Надесь, удалось. RSA использует разложение больших чисел (несколько сот разрядов) на простые множители, что требует большого объема вычислений и эта особенность определяет стойкость данного шифра. Первым этапом асимметричного шифрования является создание получателем шифрограмм пары ключей. Процедура создания ключей RSA заключается в следующем. В нашем примере φ(n) = (7-1)*(13-1) = 72. Функция Эйлера определяет количество целых положительных чисел, не превосходящих n и взаимно простых с n. Справка. Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме 1. Подсказка. Windows калькулятор необходимо перевести в режим "Инженерный". Указания. Создайте открытый и закрытый ключи при заданных в вашем варианте p и q. (см. таблицу простых чисел). Таблица 4.4. Таблица простых чисел (из первой сотни) Для проверки правильности своих расчетов заполните форму Для того, чтобы увидеть форму, вам необходимо установить Java плагин для вашего браузера и разрешить выполнение Java-апплетов. Если Вы пользуетесь браузером IE9 с установленным Java плагином и апплет тем не менее не работает, то возможно, что Java-апплет фильтруется ActiveX Filtering, новой функцией в IE9. Для ее отключения выберите Сервис/Безопасность и снимите галочку с Фильтрация ActiveX. Дешифрируйте шифрограмму с помощью закрытого ключа. Для проверки правильности своих расчетов заполните форму Для того, чтобы увидеть форму, вам необходимо установить Java плагин для вашего браузера и разрешить выполнение Java-апплетов. Если Вы пользуетесь браузером IE9 с установленным Java плагином и апплет тем не менее не работает, то возможно, что Java-апплет фильтруется ActiveX Filtering, новой функцией в IE9. Для ее отключения выберите Сервис/Безопасность и снимите галочку с Фильтрация ActiveX. Во второй части мы рассмотрим популярный алгоритм RSA, где при шифровании используется публичный ключ. Но вначале хочу предупредить вас еще раз. Код, представленный в этой статье, предназначен только для ознакомительных целей. Криптография – весьма обширная и сложная область, и чтобы у вас не было проблем, я не рекомендую шифровать информацию при помощи моей поделки. Автор: Malarkey Во второй части мы рассмотрим популярный алгоритм RSA, где при шифровании используется публичный ключ. Но вначале хочу предупредить вас еще раз. Код, представленный в этой статье, предназначен только для ознакомительных целей. Криптография – весьма обширная и сложная область, и чтобы у вас не было проблем, я не рекомендую шифровать информацию при помощи моей поделки. Алгоритм RSA Шифрование с использованием публичного ключа Шифрование при помощи публичного ключа используется повсеместно. Если вы хотя бы раз оплачивали что-то в интернете, то уже пользовались этим методом (я надеюсь!). Сразу же возникает вопрос о том, как работает эта защита. Если я ввожу номер своей кредитной карты, чтобы что-то купить, почему кроме адресата никто не может подсмотреть эти сведения? Приведу метафору. Чтобы открыть сейф, вам требуется ключ (или молоток, но, к счастью, сейфы и замки защищены от такого рода деятелей). В шифровании с использованием публичного ключа происходит примерно то же самое. Вы показываете замок на всеобщее обозрение, но ключ от этого замка есть только у избранных, а другими методами открыть дверь практически невозможно. Демо-программа на базе алгоритма RSA Рисунок 1: Процедура шифрования, дешифрования и цифровой подписи при помощи алгоритма RSA У программы есть дополнительные опции (см. рисунок ниже), позволяющие задавать собственные ключи. Рисунок 2: Другие опции демонстрационной программы Математическая сторона вопроса RSA во многом схож с алгоритмом Диффи-Хеллмана, поскольку и там и там используется модулярная арифметика. Ниже по шагам рассказывается, как генерируется публичный и секретный ключ. Теперь по шагам рассмотрим процесс шифрования и дешифрования: Рискну предположить, что многим из вас интересно, как взломать систему, построенную на основе алгоритма RSA. Злоумышленник знает числа n и e. Если взломщик сможет найти число t, то вычислит секретный ключ. Задача заключается в том, чтобы факторизовать публичный ключ. Однако целочисленная факторизация – довольно сложная задача, и именно поэтому алгоритм RSA довольно устойчив. Возможно, когда появятся квантовые машины, вычислить секретный ключ не будет составлять особого труда, но сейчас достаточной длинный ключ сможет защитить наши данные. Дополнительные размышления Поскольку ключ шифрования может быть раскрыт произвольно, этот ключ также называется открытым ключом. Ключ дешифрования никогда не должен разглашаться и может храниться только у вас, поэтому он также называется закрытым ключом. Открытый ключ и закрытый ключ являются один за другим. Соответственно, файл, зашифрованный открытым ключом, может быть расшифрован только соответствующим закрытым ключом. Отправителю нужно знать только ключ шифрования. Получателю нужно только знать ключ дешифрования. Ключ дешифрования не может быть получен злоумышленником. Ключи шифрования получают перехватчики RSA - это криптографический алгоритм с открытым ключом, и его шифрование можно выразить формулой: Шифрованный текст = Открытый текст ^ E mod N Шифрование RSA предназначено для нахождения E power mod N открытого текста, поэтому любой может завершить операцию шифрования, только зная E и N. E и N - открытые ключи алгоритма RSA. Расшифровку также можно выразить формулой: Открытый текст = зашифрованный текст ^ D mod N D и N служат закрытым ключом алгоритма RSA. Давайте сегодня узнаем о различных методах присваивания переменных в Makefile! Смысл тяжелой работы, чтобы бедность больше не ограничивать свое воображение! Добавьте QQ, чтобы вместе учиться и обменив. Портал Луогу БЗОЙ Портал Описание заголовка Bessie likes downloading games to play on her cell phone, even though she doesfind the small touch screen rather cumbersome to use with her large hooves. Sh. Читайте также: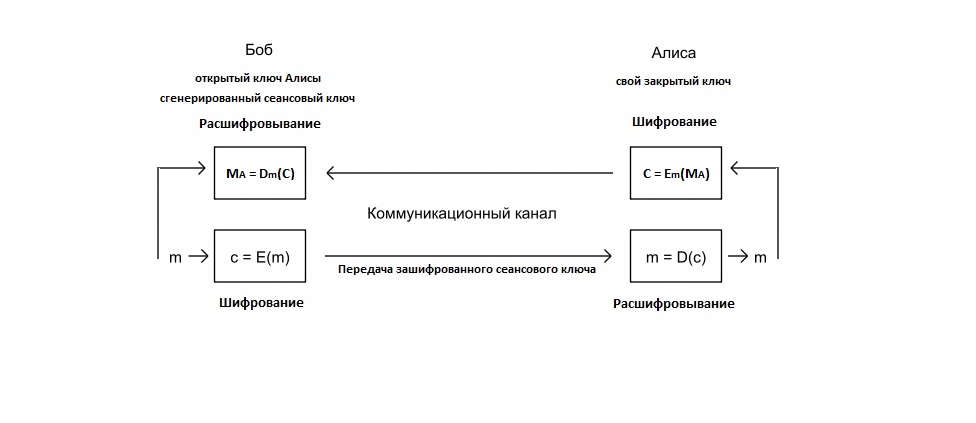
Шаг первый. Подготовка ключей
Шаг второй. Шифрование
Шаг третий. Расшифровка
В чём гарантия надёжности шифрования
А как это всё работает на практике?
Немного о сложностях
Задание на самостоятельное выполнение
Вариант p q Вариант p q 1 19 73 14 71 79 2 29 73 15 19 43 3 17 29 16 13 61 4 23 61 17 41 79 5 13 31 18 13 53 6 23 31 19 59 61 7 53 73 20 13 83 8 31 37 21 13 19 9 17 37 22 19 29 10 23 79 23 17 67 11 13 41 24 13 17 12 23 41 25 31 73 13 17 41 26 31 67
1 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 
Задание на самостоятельное выполнение
Задание на самостоятельное выполнение
Вариант Криптограмма Вариант Криптограмма 1 1127, 1310, 347, 1, 655, 261 14 2949, 4840, 3887, 4765, 875, 1 2 1, 1423, 1841, 254, 134, 777 15 190, 522, 439, 497, 447, 1 3 17, 361, 339, 304, 469, 225 16 466, 543, 472, 269, 163, 437 4 1071, 1, 606, 449, 1215, 472 17 1701, 199, 384, 2051, 2561, 330 5 379, 1, 396, 46, 1, 14 18 546, 680, 95, 62, 227, 100 6 219, 40, 468, 545, 1, 82 19 324, 2414, 615, 718, 2497, 1100 7 481, 1939, 1, 1655, 1123, 2957 20 1005, 271, 266, 967, 1030, 961 8 219, 205, 738, 894, 205, 1005 21 76, 227, 148, 177, 174, 4 9 427, 1, 499, 181, 232, 441 22 89, 474, 187, 113, 1, 474 10 1198, 1592, 591, 1, 1064, 951 23 322, 811, 573, 99, 1, 38 11 191, 251, 479, 346, 1, 251 24 76, 86, 152, 58, 142, 130 12 520, 16, 633, 623, 10, 468 25 445, 1483, 274, 1765, 233, 1154 13 576, 142, 639, 421, 208, 608 26 1811, 1, 1235, 844, 866, 214 Тест 4.3. Расшифровка криптограммы



Криптография - система асимметричного шифрования - введение и RSA
Введение:
Коммуникационный процесс криптографии с открытым ключом:

Пример асимметричного шифрования: алгоритм RSA
шифрование
Расшифровать

Шаг 1. Создайте закрытый ключ и открытый ключ

Шаг 2. Создайте файл закрытого ключа

Шаг 3. Создайте файл открытого ключа

шифрование

Расшифровать

Функции вызова

Проблемы с криптографией с открытым ключом
Интеллектуальная рекомендация

[Makefile от более мелких к более глубоким полная запись обучения 4] Переменные и различные методы присвоения
[Luogu P3147] [BZOJ 4576] [USACO16OPEN]262144


