Как оценивать объем памяти необходимый для хранения текстовых данных
Встречаются гибридные решения, когда текст хранится в наборе массивов, которые, в свою очередь, объединены в список. Казалось бы, такой подход позволяет объединить преимущества массивов и списков (быстрая вставка/удаление при низких накладных расходах по памяти). Однако такое решение сложно в реализации. Также оно приводит к фрагментации памяти.
Предлагаю вашему вниманию эффективную структуру данных для хранения редактируемого текста, которая проста в реализации, имеет константные накладные расходы по памяти и быструю вставку/удаление в произвольном месте. Также она позволяет эффективно редактировать файлы, которые целиком не умещаются в оперативную память.
Описание
Такая структура данных называется в английской терминологии Gap Buffer. Русское название мне неизвестно, встречается только термин «буферное окно» в русской Википедии. Не знаю, правда, доверять такому переводу термина или нет.
Анализ
- Операции вставки и удаления — дешевые: O(1) как при вставке отдельного символа, так и их группы (например, вставка из буфера обмена).
- Накладные расходы по памяти — низкие: O(1). Нужно хранить только положение курсора и общий размер буфера.
- Операция поиска элемента по индексу — дешевая: O(1).
- Операция копирования участка содержимого (например, для копирования в буфер обмена или сохранения текста на диск) — O(n), где n — размер копируемого участка. Сложность такая же, как для массива.
Таким образом, Gap Buffer эксплуатирует то свойство процесса редактирования текста, что операции вставки и удаления всегда происходят в том месте, где находится курсор; в свою очередь, перемещения курсора обычно бывают невелики.
Вариации
1. Теневой курсор записи
В своей базовой реализации Gap Buffer все же может вызывать нежелательные задержки. Например, при поиске текста или использовании закладок могут происходить значительные перемещения курсора. Также не всякое перемещение курсора по тексту сопровождается редактированием. Отсюда решение: ввести невидимый пользователю «курсор записи», который соответствует разрыву в Gap Buffer. Этот курсор перемещается только тогда, когда пользователь начинает вставку или удаление текста. При простых же перемещениях видимого курсора по тексту или замене (то есть когда общий размер текста не меняется) курсор записи не перемещать. Тем самым устраняются задержки при любых случайных перемещениях видимого курсора при просмотре текста, использовании закладок, поиска и т.д.
2. Редактирование файлов, которые не умещаются в оперативную память
В нашу эпоху оперативной памяти гигабайтного размера мало кто реализует редакторы, которые обходятся без полной загрузки текста в память. Большинство созданных людьми документов умещаются в нее, поэтому просто нет смысла усложнять редактор. Однако иногда возникает необходимость редактировать большие файлы, которые не умещаются даже в память сегодняшних компьютеров. Это могут быть машинно-генерированные данные, такие как лог-файлы или текстовое представление записи с каких-нибудь датчиков или приборов.
С помощью Gap Buffer можно эффективно реализовать редактирование файлов, размер которых превышает размер оперативной памяти компьютера. Можно заметить, что Gap Buffer фактически представляет собой два стека, один из которых хранит данные до курсора, а второй — после курсора. Первый из стеков растет вверх, а второй — вниз. Отсюда идея: реализовать оба стека в виде файлов, при этом храня в оперативной памяти только те их участки, которые находятся ближе к вершине.
Стек в памяти может расти вверх или вниз, а стек, реализованный в виде файла, может расти только вверх. Только к концу файла мы можем дописывать данные или наоборот, удалять их оттуда. Если вернуться теперь к операциям с памятью и рассмотреть стеки, растущие в разные стороны — то видно, что в стеке, растущем вверх, данные располагаются в прямом порядке по отношению к последовательности помещения их на стек, а в стеке, растущем вниз — в обратном порядке. Так что, если мы хотим реализовать Gap Buffer в виде двух стеков, растущих вверх — нам придется поменять порядок элементов во втором стеке, который хранит текст после курсора. Поэтому тот временный файл, который содержит данные после курсора, должен их содержать в обратном порядке, задом наперед.
Во временных файлах мы будем хранить не все содержимое стеков, а только их нижнюю часть. Верхняя часть будет располагаться в оперативной памяти, образуя как бы «локальный» Gap Buffer и позволяя пользователю, как и прежде, быстро редактировать текст и перемещаться по нему в некоторых пределах. При перемещениях курсора по тексту за пределы загруженного в память участка, его часть, наиболее далекая от курсора, будет сохраняться в один из временных файлов, а из другого будет подгружаться недостающая часть.
По окончании редактирования текста мы просто перемещаем курсор в его конец. Весь текст попадает в первый стек, растущий вверх, то есть первый временный файл. В оперативной памяти, возможно, остается еще кусок текста — его просто дописываем к файлу. После этого первый временный файл содержит сохраненный текст.
Можно реализовать еще несколько оптимизаций. При открытии файла, например, курсор обычно находится в его начале. Весь текст поэтому должен располагаться во втором стеке, то есть мы должны практически всё исходное содержимое редактируемого файла скопировать во второй временный файл задом наперед. Это длительная операция. Ее можно избежать, если отложить создание второго временного файла до тех пор, пока в этом не возникнет необходимость. То есть до тех пор, пока содержимое хвоста исходного файла полностью совпадает с содержимым второго стека. В этот период, вместо использования второго временного файла, мы можем подгружать информацию из исходного файла. Для создания второго временного файла, таким образом, придется сначала переместить курсор по тексту на расстояние, превышающее размер свободной оперативной памяти, потом что-нибудь там отредактировать, а потом вернуться назад, к началу текста.
Такую же оптимизацию можно реализовать и для первого временного файла. Не создавать его до тех пор, пока в нем не возникнет необходимость. А возникнет она не ранее, чем содержимое находящейся на диске части первого стека перестанет совпадать с начальным участком исходного файла. Также можно использовать «теневой курсор записи» и тем самым избежать ненужных операций копирования при перемещениях курсора по тексту без редактирования. Тогда, если пользователь далеко перемещает курсор по тексту без редактирования, скорость работы будет не хуже, чем у программы простого просмотра текста без полной его загрузки в память.
Реализованное описанным способом редактирование текста без полной его загрузки в память имеет, таким образом, умеренные накладные расходы по дисковому пространству: для временных файлов требуется место, равное размеру текста.
Интересно, что даже если текст большого объема в принципе влезает в оперативную память, при использовании редактора, который не загружает его целиком, такой документ будет быстрее открываться. Снова-таки повышение удобства для пользователя.
Заключение
Я уже не первый раз сталкиваюсь с тем, что некоторые технологии, разработанные для старых компьютеров с ограниченными возможностями, оказываются в наше время забытыми, что приводит к распространению неэффективных решений. Надеюсь, что описанное в этой статье «тайное знание предков» поможет появлению на свет хороших текстовых редакторов.
Код ОГЭ по информатике: 2.1.3. Оценка количественных параметров информационных объектов. Объем памяти, необходимый для хранения объектов
Оценка количества информации
Впервые объективный подход к измерению количества информации был предложен американским инженером Р. Хартли в 1928 г. Позже, в 1948 г., этот подход обобщил создатель общей теории информации К. Шеннон.
По приведенной выше формуле можно рассчитать, какое количество информации I несет каждый из знаков этой системы. Если в алфавите знаковой системы N знаков, то каждый знак несет количество информации: I = log2 N

Текстовая информация состоит из букв, цифр, знаков препинания, различных специальных символов. Для кодирования текстовой информации используют различные коды. Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки. Существуют различные таблицы кодировок текстовой информации.
Распространенная таблица кодировки ASCII (читается «аски», American Standard Code for Information Interchange — стандартный американский код для обмена информацией) использует 1 байт для кодов информации. Если код каждого символа занимает 1 байт (8 бит), то с помощью такой кодировки можно закодировать 2 8 = 256 символов.
Таблица ASCII состоит из двух частей. Первая, базовая часть, является международным стандартом и содержит значения кодов от 0 до 127 (для цифр, операций, латинского алфавита, знаков препинания). Вторая, национальная часть, содержит коды от 128 до 255 для символов национального алфавита, т. е. в национальных кодировках одному и тому же коду соответствуют различные символы.
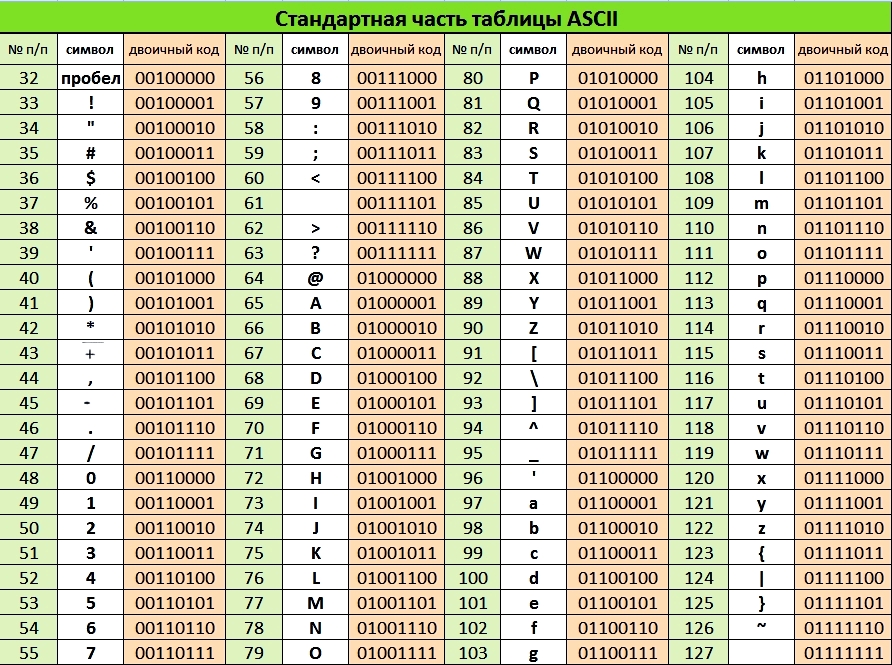
В настоящее время существует несколько различных кодировок второй части таблицы для кириллицы — КОИ8–Р, KOI8–U, Windows, MS–DOS, Macintosh, ISO. Наиболее распространенной является таблица кодировки Windows–1251. Из–за разнообразия таблиц кодировки могут возникать проблемы при переносе русского текста между компьютерами или различными программами.
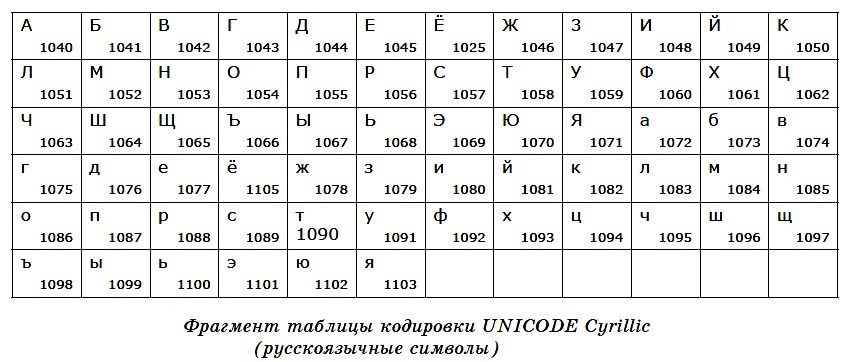
Поскольку объем в 1 байт явно мал для кодирования разнообразных и многочисленных символов мировых алфавитов, была разработана система кодирования Unicode. В ней для кодирования символа отводится 2 байта (16 бит). Это означает, что система позволяет закодировать 2 16 = 65 536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.
Количество графической информации
Растровое графическое изображение состоит из отдельных точек — пикселей, образующих строки и столбцы.
Основные свойства пикселя — его расположение и цвет. Значения этих свойств кодируются и сохраняются в видеопамяти компьютера.
Качество изображения зависит от пространственного разрешения и глубины цвета.
Разрешение — величина, определяющая количество точек (пикселей) на единицу площади.
Глубина цвета — объем памяти (в битах), используемой для хранения и представления цвета при кодировании одного пикселя растровой графики или видеоизображения.
Для графических изображений могут использоваться различные палитры — наборы цветов. Количество цветов N в палитре и количество информации I, необходимое для кодирования цвета каждой точки, связаны соотношением: N = 2 I
Чтобы определить информационный объем видеоизображения, необходимо умножить количество информации одного пикселя на количество пикселей в изображении: I = Iпикселя • X • Y, где Х — количество точек изображения по горизонтали, Y — количество точек изображения по вертикали.
Существует несколько цветовых моделей для количественного описания цвета. В основе модели RGB (сокращение от англ. Red, Green, Blue) лежат три основных цвета: красный, зеленый и синий. Все другие цвета создаются с помощью смешения их оттенков. Например, при смешивании красного и зеленого цветов получим желтый, красного и синего — пурпурный, зеленого и синего — бирюзовый. Если смешать все три основные цвета максимальной яркости, получим белый цвет.
Если один цвет имеет 4 оттенка, то общее количество цветов в модели RGB будет составлять 4 • 4 • 4 = 64. При 256 оттенках для каждого цвета общее количество возможных цветов будет равно 256 • 256 • 256 = 16 777 216 ≈ 16,7 млн.
В современных компьютерах для представления цвета обычно используются от 2–х до 4–х байт. Два байта (16 бит) позволяют различать 2 16 , то есть 65 536 цветов и оттенков. Такой режим представления изображений называется High Color. Четыре байта (32 бита) обеспечивают цветную гамму в 2 32 , то есть 4 294 967 296 цветов и оттенков (приблизительно 4,3 миллиарда). Такой режим называется True Color.
В графических редакторах применяются и другие цветовые модели. Например, модель CMYK — она основана на цветах, получающихся при отражении белого света от предмета: бирюзовом (англ. Cyan), пурпурном (англ. Magenta), желтом (англ. Yellow). Эта модель применяется в полиграфии, где чаще всего употребляется черный цвет (ключевой, англ. Key).

Измерение объемов звуковой информации
Звук является непрерывным сигналом. Для использования звука в компьютере его преобразуют в цифровой сигнал. Это преобразование называется дискретизацией: для кодирования звука производят его измерение с определенной частотой (несколько раз в секунду). частота дискретизации и точность представления измеренных значений определяют качество представления звука в компьютере. Чем выше частота дискретизации и чем больше количество разных значений, которыми можно характеризовать сигнал, тем выше качество отображения звука.
В современных компьютерах обычно применяется частота дискретизации в 22 кГц или 44,1 кГц (1 кГц — это тысяча измерений за 1 секунду), а для представления значения сигнала выделяются 2 байта (16 бит), что позволяет различать 2 16 , то есть 65 536 значений.







Разбор задания №1 (ОГЭ)
Задание №1. Определение объёма памяти, необходимого для хранения текстовых данных.
Уровень сложности: базовый; макс. балл за задание: 1; примерное время выполнения: 3 минуты.
Знать: дискретная форма представления информации; единицы измерения количества информации.
Уметь: оценивать объём памяти, необходимый для хранения текстовых данных; оценивать числовые параметры информационных объектов и процессов: объём памяти, необходимый для хранения информации; скорость передачи информации.
Пример задания.
В одной из кодировок Unicode каждый символ кодируется 16 битами.
Вова написал текст (в нём нет лишних пробелов):
«Чиж, грач, стриж, гагара, пингвин, ласточка, жаворонок, свиристель, буревестник, вертиголовка – птицы».
Ученик вычеркнул из списка название одной птицы. Заодно он вычеркнул ставшие лишними запятые и пробелы – два пробела не должны идти подряд. При этом размер нового предложения в данной кодировке оказался на 18 байт меньше, чем размер исходного предложения.
Напишите в ответе вычеркнутое название птицы.
Разбор задания: если мы вычеркнем из текста название любой птицы, то вместе с ним мы удалим один лишний пробел и одну запятую. Следовательно, так как один символ равен 2 байта (16 бит = 2 байта), то мы отнимем 2 байта (вес пробела), плюс 2 байта (вес запятой). По условию размер нового предложения стал меньше на 18 байт, следовательно 18 - 2 - 2 = 14 байт - это размер слова (названия слова). Так как каждый символ весит 2 байта, то 14 / 2 = 7 - это количество символов в названии птицы. Осталось отыскать его в тексте. Этим названием оказалось слово ПИНГВИН.
Ответ: ПИНГВИН.
Разберём ещё пару задачек.
Пример задания.
В одной из кодировок Unicode каждый символ кодируется 16 битами. Ученик написал текст (в нем нет лишних пробелов):
«Близнецы, дева, рак, телец, стрелец – знаки Зодиака».
Ученик вычеркнул из списка название одного из знаков Зодиака. Заодно он вычеркнул ставшие лишними запятые и пробелы – два пробела не должны идти подряд. При этом размер нового предложения в данной кодировке оказался на 14 байт меньше, чем размер исходного предложения. Напишите в ответе вычеркнутое название знака Зодиака.
Разбор задания: по примеру решения первой задачки, если мы вычеркнем из текста название знака Зодиака, то вместе с ним мы удалим один лишний пробел и одну запятую. Следовательно, так как один символ равен 2 байта (16 бит = 2 байта), то мы отнимем 2 байта (вес пробела), плюс 2 байта (вес запятой). По условию размер нового предложения стал меньше на 14 байт, следовательно 14 - 2 - 2 = 10 байт - это размер слова (названия слова). Так как каждый символ весит 2 байта, то 10 / 2 = 5 - это количество символов в названии знака Зодиака. Осталось отыскать его в тексте. Этим названием оказалось слово ТЕЛЕЦ.
Ответ: ТЕЛЕЦ.
Пример задания (для самостоятельного разбора).
В одной из кодировок Unicode каждый символ кодируется 16 битами.
Вова написал текст (в нём нет лишних пробелов):
«Чиж, грач, стриж, гагара, пингвин, ласточка, жаворонок, свиристель, буревестник, вертиголовка – птицы».
Ученик вычеркнул из списка название одной птицы. Заодно он вычеркнул ставшие лишними запятые и пробелы – два пробела не должны идти подряд. При этом размер нового предложения в данной кодировке оказался на 18 байт меньше, чем размер исходного предложения.
Напишите в ответе вычеркнутое название птицы.
ОГЭ по информатике
Демоверсия ОГЭ по информатике 2021
Официальная демоверсия ОГЭ 2021 по информатике утверждена ФИПИ.
Задание 4 ОГЭ по информатике
Анализировать простейшие модели объектов необходимо для выполнения задания №4 ОГЭ по информатике.
Задание 3 ОГЭ по информатике
Определять истинность составного высказывания необходимо для выполнения задания №3 ОГЭ по информатике.
Задание 2 ОГЭ по информатике
Уметь декодировать кодовую последовательность необходимо для выполнения задания №2 ОГЭ по информатике.
Задание 1 ОГЭ по информатике
Оценивать объем памяти, необходимый для хранения текстовых данных необходимо для выполнения задания №1 ОГЭ по информатике.
Варианты досрочного ОГЭ 2020 по информатике от ФИПИ
Два досрочных варианта ОГЭ 2020 по информатике от ФИПИ с ответами и критериями оценивания.
ОГЭ по информатике 2020 демоверсия (9 класс)
Подготовку к ОГЭ 2020 по информатике для выпускников 9 классов целесообразно начинать с ознакомления с демонстрационными вариантами. Так же открытый банк заданий ФИПИ содержит примеры реальных вариантов, включаемых в тесты для экзаменов.
Информатика ОГЭ 2019 - перевод баллов в оценки
Перевод баллов ОГЭ 2019 по информатике (ГИА 9 класс) в оценку можно узнать в рекомендациях, опубликованных на официальном сайте ФИПИ.
ОГЭ по информатике демоверсия 2019 года от ФИПИ
До начала нового учебного года на официальном сайте ФИПИ опубликованы демоверсии ОГЭ 2019 по информатике (ГИА 9 класс).
Подготовку к ОГЭ 2019 по информатике для выпускников 9 классов целесообразно начинать с ознакомления с демонстрационными вариантами. Так же открытый банк заданий ФИПИ содержит примеры реальных вариантов, включаемых в тесты для экзаменов.
Демоверсия ОГЭ по информатике от ФИПИ 2018 год
На официальном сайте ФИПИ опубликованы демоверсии ОГЭ 2018 года по информатике (ГИА 9 класс).
Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 22 балла.
Результаты экзамена ОГЭ по информатике в 9 классе могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы может быть показатель, нижняя граница которого соответствует 15 баллам.
ОГЭ информатика баллы и оценки 2018 год
Максимальный балл ОГЭ по информатике (ГИА 9 класс) в 2018 году - 22
Проходной балл в профильные классы - 15
Минимальный балл - 5 (оценка 3)
Сколько нужно набрать баллов на ОГЭ по информатике, что бы получить 3, 4, или 5 можно узнать в рекомендациях, опубликованных на сайте ФИПИ.
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы может быть показатель, нижняя граница которого соответствует 15 баллам.

Методические материалы для подготовки к ОГЭ по информатике. В презентации представлен теоретический и практический материал по данной теме. Учащиеся научатся оценивать объем памяти, необходимый для хранения текстовых данных. Приведены примеры решения задач. Есть задачи для самостоятельного решения.
Полный текст материала Презентация к уроку информатики "Количественные параметры информационных объектов"; 9 класс смотрите в скачиваемом файле.
На странице приведен фрагмент.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий



Упражнения на технику чтения и понимания прочитанного
Тонкости и секреты работы в Яндекс.Почте
Как работать с детьми с СДВГ в обычном классе?
Жаль что у самих преподавателей нет желания разрешить конфликт. Им дана власть нДевиз: поднемите руки выше!
по
Отправляя материал на сайт, автор безвозмездно, без требования авторского вознаграждения, передает редакции права на использование материалов в коммерческих или некоммерческих целях, в частности, право на воспроизведение, публичный показ, перевод и переработку произведения, доведение до всеобщего сведения — в соотв. с ГК РФ. (ст. 1270 и др.). См. также Правила публикации конкретного типа материала. Мнение редакции может не совпадать с точкой зрения авторов.
Для подтверждения подлинности выданных сайтом документов сделайте запрос в редакцию.
О работе с сайтом
Мы используем cookie.
Публикуя материалы на сайте (комментарии, статьи, разработки и др.), пользователи берут на себя всю ответственность за содержание материалов и разрешение любых спорных вопросов с третьми лицами.
При этом редакция сайта готова оказывать всяческую поддержку как в публикации, так и других вопросах.
Если вы обнаружили, что на нашем сайте незаконно используются материалы, сообщите администратору — материалы будут удалены.
Читайте также:


